HPPC参数辨识时间域对电池模型精度影响的研究

赵秀亮，赵明明，杨政宇，乔思秉，王丽梅,，陈 军

(1.江苏大学 汽车与交通工程学院， 江苏 镇江 212013；2.江苏大学 汽车工程研究院， 江苏 镇江 212013；3.江苏悦达专用车有限公司， 江苏 盐城 224007)

0 引言

车用动力电池组通常是由成百上千的单体电池串并联构成，各单体间的差异可能对整车电池系统的寿命、安全性能带来严重影响[1-2]。为此，通过配备电池管理系统(battery management system,BMS)对电动汽车电池状态进行监测与管理。目前主流的状态估计方法有模型驱动型和数据驱动型，模型驱动型具有闭环估计的特点，并且计算成本和估计精度之间可以取得很好的平衡，而模型驱动型的核心是建立准确的模型及精确的模型参数[3-4]。因此，寻求合适的描述电池模型，准确辨识电池模型参数成为目前研究的重点。

当前常用的电池模型主要有电化学模型[5-6]、等效电路模型[7-8]、神经网络模型[9-10]。等效电路模型利用电容、电阻、电压源、电流源等，通过不同的组合电路描述电池充放电特性。物理意义明确、数学表达简单，可以很好地模拟电池动态特性，且复杂度低，成为目前最常用的一类电池模型。基于电池模型的参数辨识分为离线参数辨识和在线参数辨识[11]。与离线辨识相比，在线参数辨识具有实时性、精确度高、鲁棒性好的特点，尤其是在电动车运行工况变化时，在线参数辨识更具优势[12]。虽然在线参数辨识已经成为目前的主流研究方向，但在线参数辨识多基于递推最小二乘法(recursive least-squares,RLS)等优化算法进行，参数辨识的准确性受制于辨识参数数目、参数辨识限定范围等，多个参数同时辨识时或初始参数范围超界等易导致辨识参数偏移准确值或辨识算法发散等[13]。离线参数辨识可基于实验室实测数据，以模型的预测值与实测值的高度拟合为目标完成参数辨识，快速的探索特定工况下电池参数变化规律及其与电池性能间的关联性，也可以为在线参数辨识提供参考，所以离线参数辨识仍然是电池建模及特性研究不可或缺的方法。

离线参数辨识多是通过混合脉冲功率性能测试(hybrid pulse power characteristic,HPPC)实验进行的。王维强[14]、Huang等[15]分别基于PNGV模型和改进的PNGV模型，由HPPC实验的零输入响应阶段进行参数辨识，认为两种模型都可以很好地模拟电池特性。Deng等[16]以70 Ah电池为研究对象，通过对HPPC实验脉冲放电零状态响应阶段进行指数拟合，获取二阶RC等效电路模型参数。罗勇[17]、吴小慧等[18]利用最小二乘法对零输入响应的“回弹上升”阶段进行拟合，获取不同荷电状态(state of charge,SOC)下的二阶RC等效电路模型的极化参数。张绍虹等[19]通过零输入响应—“回弹上升”阶段辨识模型参数，对比了5、20、30 ℃下的Thevenin等效电路模型精度，结果表明，高温下电压估算精度较好，低温条件下精度较差。Li等[20]进一步研究了HPPC实验用于离线参数辨识存在的问题，通过零状态响应阶段提取二阶RC等效电路模型参数，设置了4种不同的HPPC实验脉冲与静置时间，经过仿真与实验发现在脉宽和静置时间都较小的情况下，通过增加其中任何一个阶段都可以提高参数辨识的精度。

综合之前研究者对离线参数辨识问题的研究，发现通常使用HPPC实验的零输入响应—“回弹特性”阶段或零状态响应阶段进行参数辨识，将研究重点放在建立不同的等效电路模型上；有部分学者发现HPPC实验脉冲时间和静置时间会影响模型精度，低温下需对模型参数加以修正。但上述研究缺少不同温度下模型参数对模型精度影响和相应偏差修正问题的研究。本文将基于HPPC实验对比不同温度、不同时间域下模型参数辨识的精度，分析参数辨识精度与温度及时间域的关系，从而改善温度较低时模型精度差的问题。

1 实验平台搭建及方案设计

1.1 实验平台搭建

本文研究使用的是索尼公司生产的US18650VTC6锂离子电池，该电池的主要参数如表1所示。实验采用的电池测试平台主要包括电池测试系统、温度实验箱以及用于保存实验数据的上位机。其中，宁波拜特NBT5V20AC16-T测试系统能够实现恒流、恒压、斜坡、脉冲、自定义工况等多种充放电方式，另外还可以对电池电压、电流、温度等进行实时监测。深圳科晶MSK-TE906-150L温度实验箱负责给电池提供一个恒温稳定的工作环境。

表1 实验用电池性能参数

1.2 实验方案设计

在25 ℃下对电池进行容量标定，选取标定容量为2.75 Ah的6块老化程度一致的单体电池。然后分别在5、25、55 ℃下各选取2块电池进行HPPC实验，之后在每个温度下再进行0.5 C，1 C的恒流放电实验。

1.2.1HPPC实验

在5、25、55 ℃ 3种温度下根据《美国Freedom CAR电池实验手册》，对电池进行HPPC实验测试，测试系统采样频率为1 Hz。HPPC测试中通过对不同SOC点采用充放电脉冲激励对电池进行充放电操作，以此获得不同SOC下的动力电池的动态特性参数，HPPC实验流程如表2。HPPC实验每完成一个循环SOC下降约5%，由于5 ℃下以5 C对电池进行充放电容易触发测试设备的过压保护机制，所以5 ℃下的HPPC实验工步3及工步4改成3 C恒流充放电，3个温度下的其他工步一致。

表2 HPPC实验流程

1.2.2恒流放电实验

为了验证建立的电池模型以及参数辨识的准确性，在5、25、55 ℃进行了不同倍率恒流放电实验，实验流程如表3。

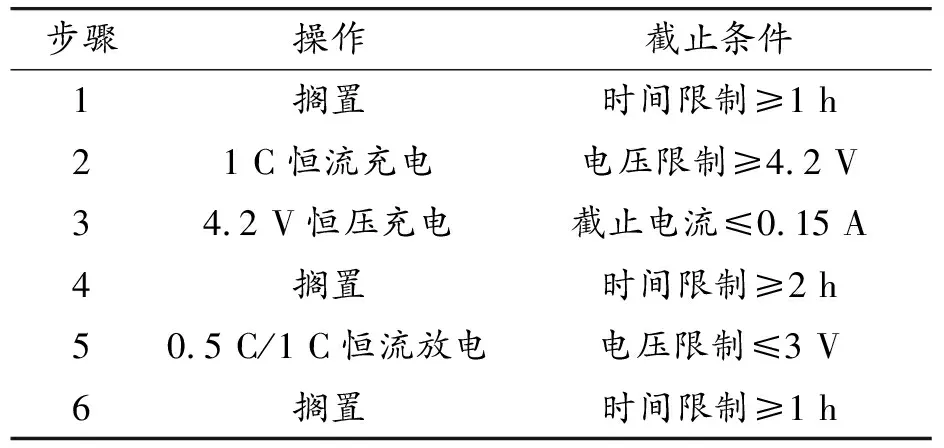
表3 恒流放电实验流程

2 离线参数辨识方法讨论

2.1 等效电路模型原理

图1为Thevenin等效电路模型原理图，其中UOCV表示开路电压，R0表示欧姆内阻，RC网络用于描述电池的极化现象，I表示负载电流。

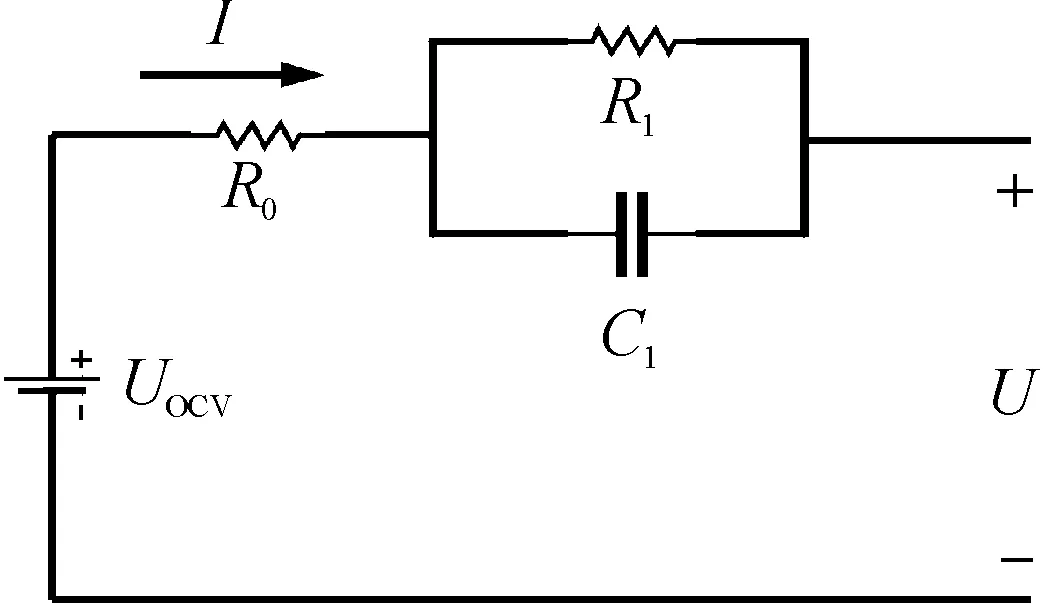
图1 Thevenin等效电路模型原理

基于基尔霍夫定律，Thevenin等效电路模型的状态空间方程如下：

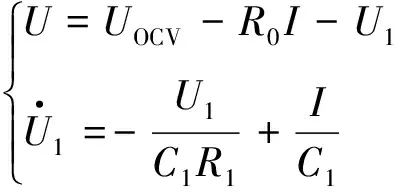
(1)

式中：R1表示极化电阻；C1表示极化电容；U1表示极化电压，即R1C1两端的电压；U表示端电压。

2.2 模型参数离线辨识

以HPPC实验某次循环工况介绍参数辨识方法，图2为25 ℃下、SOC为0.6时的HPPC循环工步电流、电压变化曲线。

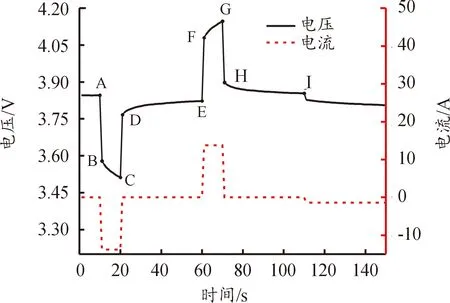
图2 HPPC循环工步电压及电流变化

2.2.1开路电压辨识

HPPC实验每个完整的脉冲阶段都有一段以0.5 C恒流放电6 min的过程，SOC下降约5%，之后对电池进行2 h的静置，使开路电压(open circuit voltage,OCV)可以达到较为稳定的状态，进而得到SOC与开路电压的对应数据。5、25、55 ℃ 下的OCV-SOC关系曲线如图3，可以发现，3个温度下当SOC大于50%时对应关系基本一致，OCV比较接近；当SOC小于50%后，55 ℃的OCV随SOC的下降最快，25 ℃次之，5 ℃下的OCV下降最慢。

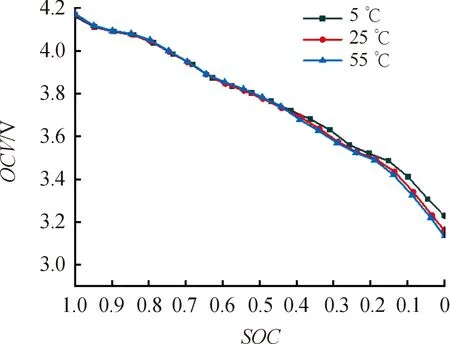
图3 OCV-SOC的对应关系

2.2.2欧姆内阻辨识

如图2所示，A到B阶段是突然受到10 s的放电脉冲激励，电压迅速从UA下降到UB，该现象是由欧姆内阻R0造成的，根据此阶段可以辨识出欧姆内阻R0，计算公式如下：

(2)

当然，CD、EF、GH阶段也可以辨识出R0，通过不同阶段计算得到的欧姆内阻相差不大。3个温度下欧姆内阻R0与SOC对应关系如图4所示，可以发现55 ℃下的欧姆内阻最小，5 ℃下的欧姆内阻最大。

图4 欧姆内阻R0与SOC对应关系

2.2.3极化参数辨识

如图2所示，B到C为脉冲放电阶段，由于电池的极化特性，端电压从UB缓慢下降到UC，放电电流对极化电容充电的过程是RC回路的零状态响应阶段。对电路进行时域分析，可得到此阶段端电压U与时间t的函数关系：

U=UOCV-IR0-IR1[1-exp(-t/τ)]

(3)

D到E为脉冲放电之后静置—“回弹上升”阶段，端电压迅速上升然后逐渐趋于稳定状态，即电池的“回弹特性”，极化电容放电的过程是RC回路的零输入响应阶段，此时端电压U与时间t的函数关系为：

(4)

式中，τ为时间常数(τ=R1C1)。

这2个过程符合指数函数关系，可描述为：

y=y0+A1exp(-x/t1)

(5)

通过对比式(3)(4)与式(5)可得：

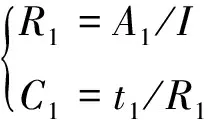
(6)

对利用F到G的脉冲充电阶段、H到I的静置—“回弹下降”阶段进行极化参数提取，方法与上述一致，故不再赘述。同时，从I开始进行的是0.5 C的6 min放电阶段，通过此阶段也可以进行模型参数提取，符合B到C阶段建立的函数关系。

3 模型建立与实验验证

3.1 仿真模型搭建

为对比不同温度下参数辨识结果的准确性，采用Matlab/Simulink中的Simscape搭建了Thevenin等效电路模型，如图5所示。

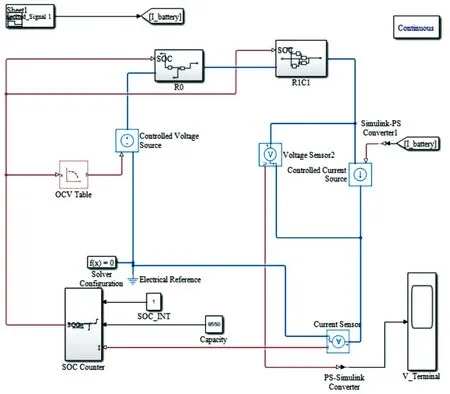
图5 Thevenin等效电路仿真模型

该模型由一个可控电压源模块代替开路电压，可变电阻模块R0作为欧姆内阻R0，一个可变电阻模块R1与可变电容模块C1组成的RC并联回路串联而成。上述模型中模块参数是通过一维查表得到不同SOC下的对应参数值，一维表的输入参数SOC是由SOC Counter模块实现的，通过设定初始SOC值和输入电流以及仿真时间，利用安时积分法求得当前时刻的SOC。整个回路计算过程便可以用来模拟电池的充放电过程，通过设置计算步长与实验数据采集频率一致，就可以将仿真与实验结果进行对比。

3.2 不同阶段参数辨识结果对比分析

3.2.110 s阶段辨识参数验证

图6、7、8分别是在5、25、55 ℃下通过HPPC实验中10 s放电过程辨识得到的参数在2种放电工况下仿真与实验结果曲线。需要说明的是，在验证过程中也进行了动态应力测试(dynamic stress test,DST)工况的验证，但对比发现，恒流工况相对DST工况，电流波动平缓，更有利于描述偏差现象，所以后面仅选择恒流工况进行分析。同时进行了10 s充电阶段辨识参数对比，结果与此类似，这里就不再给出此阶段的结果。从图6可以看出，5 ℃下，仿真值明显高于实验值，经计算，1 C放电工况最大绝对值误差达到89 mV，最大相对误差为2.57%。从图7可以看出，25 ℃下，仿真值仍高于实验值，但差值明显减小，经计算，最大相对误差在2%以内。结合图8可以看出，55 ℃下2个放电工况下，仿真值与实验值基本接近，并不存在明显的偏高现象。

3.2.240 s阶段辨识参数验证

图9、10、11分别是在5、25、55 ℃下通过HPPC实验中40 s静置阶段辨识得到的参数在2种放电工况下仿真与实验结果曲线。对比图9—11发现，40 s辨识阶段出现了与10 s辨识阶段相同的现象，5 ℃下整体相对误差明显大于25 ℃，而55 ℃下仿真平均相对误差仅为0.5%左右，表明模型参数提取的准确度与温度存在明显的相关性，这与文献[19]得到的结论基本类似。

图6 5 ℃下仿真与实验结果曲线

图7 25 ℃下仿真与实验结果曲线

图8 55 ℃下仿真与实验结果曲线

图9 5 ℃下仿真与实验结果曲线

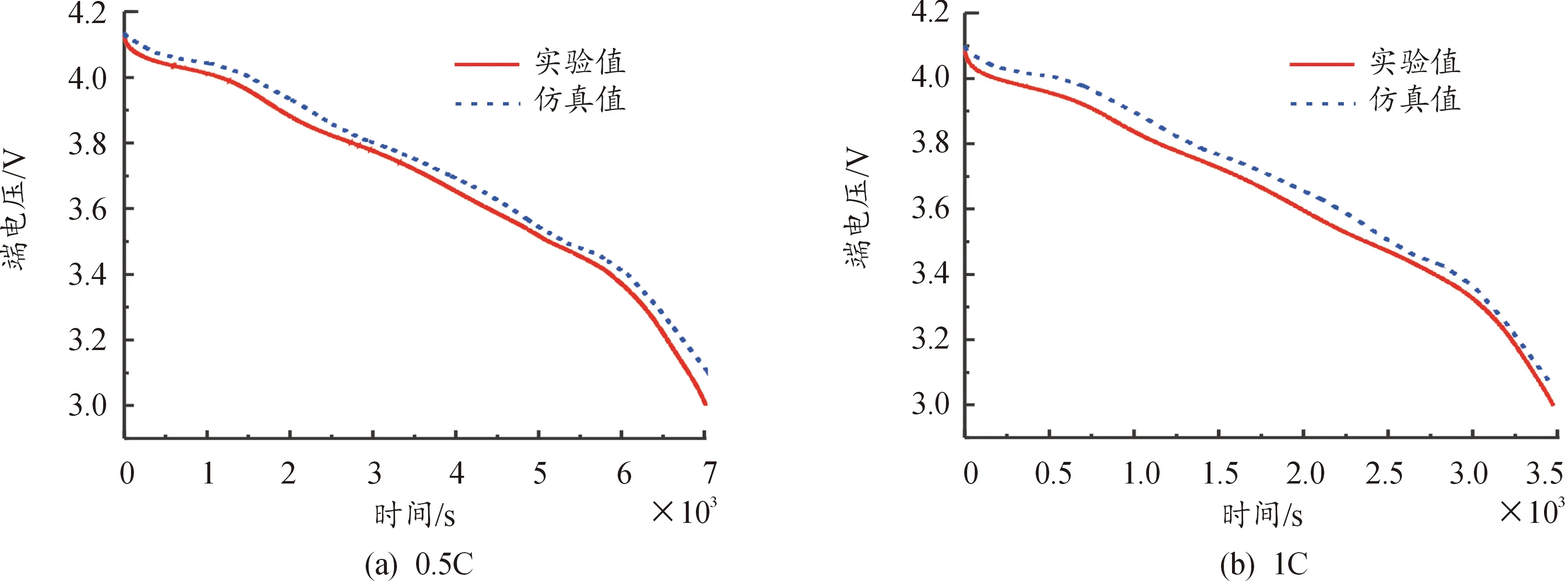
图10 25 ℃下仿真与实验结果曲线

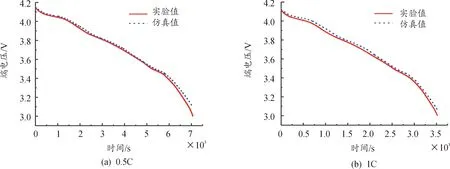
图11 55 ℃下仿真与实验结果曲线

3.3 偏差修正讨论

从上述仿真结果来看，5、25 ℃下，恒流放电工况下仿真值与实验值存在一个相对稳定的电压偏差。考虑到10 s和40 s的结论基本类似，这里进一步选择对10 s放电阶段参数辨识得到的仿真结果进行偏差修正。在恒流工况电压平台期内对仿真值与实验值做差求取均值，将该均值作为偏差修正量进行修正，结果对比如表4、5。结果表明，仿真值与实验值的偏差和放电倍率并不存在倍数相关性，因此判断在5、25 ℃下的仿真误差不是由欧姆内阻或连接阻抗造成的。5 ℃两个恒流工况下电池温升变化如图12，实验过程中整体温升不是很大，并且略微的温升主要发生在放电后期，所以也排除了放电温升对结果的影响。通过固定偏差修正后5 ℃下的最大相对误差在1.2%以内，25 ℃下的最大相对误差在1%以内。但是此偏差的修正是基于已知验证工况实验数据的基础上进行的，因此不具有实际工程价值。

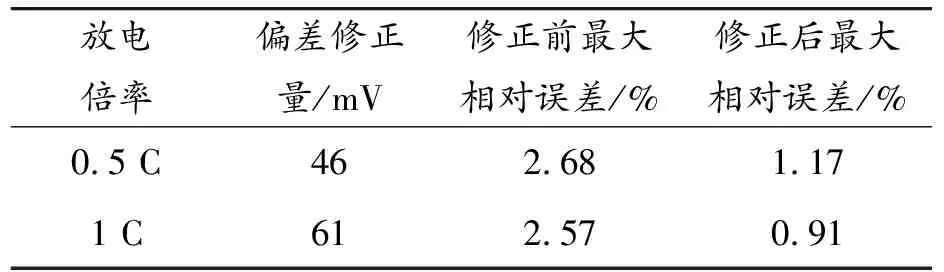
表4 5 ℃下不同倍率偏差修正结果

表5 25 ℃下不同倍率偏差修正对比

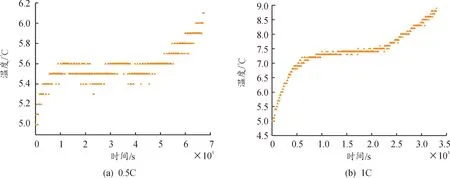
图12 5 ℃不同放电倍率下电池温度变化曲线

为了解决5、25 ℃下模型参数提取不准确的问题，结合锂离子电池本身的特性可知，电池内部是有机电解液体系，随着电池温度的升高，电池内部电化学反应加快，锂离子扩散加快，极化内阻减小[21]。也就是说，在低温环境下，电池的极化时间要长于高温环境下。若离线参数辨识统一采用固定的10 s或40 s阶段数据，极有可能造成5 ℃下的偏差明显大于25 ℃和55 ℃下的偏差的现象。考虑到如果HPPC实验设置长时间高倍率脉冲阶段可能会导致SOC变化，这里直接通过选取现有的6 min放电阶段的不同时间域进行极化参数提取，研究不同时间域提取模型参数精度与温度的关系。基于以上分析，分别选取5、25 ℃下HPPC实验数据中6 min放电阶段的前20、40、60 s时间域进行模型参数辨识，然后在不同工况下进行仿真验证。

图13是5 ℃下通过不同时间域提取的模型参数仿真结果曲线。对比图6和图13可以看出，不同时间域对结果产生了较大影响，两者间的偏差尤其在电压平台期内在逐步降低。经计算，0.5 C工况下，最大相对误差从10 s时间域下的2.68%降低到20 s时间域下的1.6%以及40 s(60 s)的1.25%，平均相对误差则从1.49%降低到了0.8%(20 s)及0.55%(40、60 s)。1 C工况下，最大相对误差从10 s时间域的2.57%降低到1.7%左右，平均相对误差从1.74%降低到了1%(20 s)和0.42%(40、60 s)。同时，考虑到仿真曲线整体的光滑度，以及最大相对误差在低SOC区域的累积结果，5 ℃下通过40、60 s的时间域进行模型参数提取更为理想。对比图9和图13(b)，还可以发现，静置阶段的40 s仿真误差明显大于放电6 min阶段的40 s，这是因为验证仿真工况为放电工况，与6 min放电工况更为接近，极化效应程度也更加接近。

图14是25 ℃下通过不同时间域提取的模型参数仿真结果曲线。经计算，0.5 C恒流放电工况下，20、40 s提取的参数下平均相对误差在0.33%以内，尤其是40 s下提取的参数最大相对误差不超过0.55%。1 C恒流放电工况下，在3组不同时间域内平均相对误差都在0.5%以内，最大相对误差在1.8%以内。

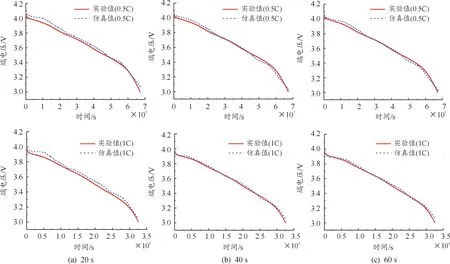
图13 5 ℃下通过不同时间域提取的模型参数仿真与实验对比曲线

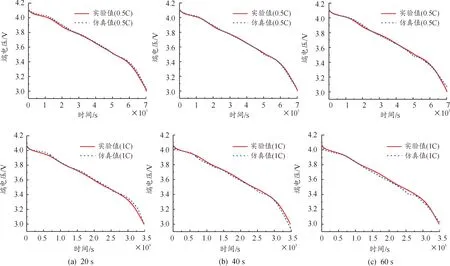
图14 25 ℃下通过不同时间域提取的模型参数仿真与实验对比曲线

综上可以看出，不同时间域对辨识的极化参数及模型精度会产生影响，在实际应用过程中，需要对电池的极化特性进行分析，从而选择合适的时间域进行模型参数的辨识，以替代现有的固定时间域的离线参数辨识，从而提高不同工况下电池模型的精度。

4 结论

1) 不同温度下辨识得到的模型参数精度不同，在对3个温度下的仿真结果进行偏差修正后发现，偏差大小与放电倍率不存在倍数相关性，排除了欧姆内阻及连接阻抗误差对仿真结果的影响；同时，根据放电工况电池温度变化，排除了温度对模型的影响，表明参数辨识精度与温度之间存在相关性。

2) 考虑到电池极化效应与温度的关系，研究了不同时间域对电池极化参数及模型精度的影响。通过改变时间域的参数辨识方法，将5 ℃下不同放电工况的平均相对误差分别降到0.55%(0.5 C)和0.42%(1 C)。同样，25 ℃下模型参数精度也得到了明显的提升。

3) 针对不同温度下基于HPPC实验进行的离线参数辨识，要结合温度选择不同的时间域。尤其是低温下，通过适当地增大用于参数辨识的时间域，可以有效地提高模型精度。