一题多解，各美其美——以一道几何题的解法探究为例

宿城第一初级中学

刘旭东 饶磊磊

一题多解，就是在不同视角下对问题进行剖析与探究.一题多解，既有助于开阔解决问题的思路,提高解决问题的能力，又可以最大限度地挖掘学生已有知识的潜在能力；它有利于培养学生的直观想象能力,发散学生的数学思维，发展学生的核心素养．

本文主要探究下列问题第(2)问的解法，剖析其解决的策略以及对教学的启迪,以供各位同仁参考，并欢迎指正.

1 问题呈现

图1

问题如图1，点E，F分别是正方形ABCD的边AB，BC的中点，DE与AF交于点H,连接BH.

(1)写出线段DE与AF的数量关系和位置关系，并证明；

(2)求∠BHD的度数.

2 思路分析

该题是由北师大版九年级上册“正方形”这一节例题改编而来，以正方形为背景考查两条线段之间的关系及求角的度数.对于第(1)小问，我们可以通过证明△ADE≌△BAF，得DE=AF,∠EAF=∠EDA，∠AED=∠BFA,进一步可得∠EHA=90°，从而AF与DE垂直且相等；第(2)问求角的度数，思考的角度较多，可以直接求解，亦可考虑用该角和其他角的关系，利用三角函数等方法求解.第(2)问思路宽，解法多，极具探究价值，具体策略如下.

图2

3 特色解法

策略一:将∠BHD放到四边形DCBH中，灵活利用其内角间的关系进行求解.

解法1：如图2，延长AF至点M，使得FM=AF，连接CM，HC，易证△ABF≌△MCF.

故∠BCM=90°，即点D，C，M共线,且AB=MC=DC,从而得到点C为DM的中点.

由(1)知AF⊥DE，即∠MHD=90°.

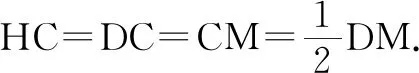
由DC=BC，得HC=BC.

故∠CBH=∠CHB,∠CHD=∠CDH.

因为∠BCD+∠CDH+∠DHB+∠CBH=360°，所以∠CDH+∠DHB+∠CBH=270°.

即∠CBH+∠BHC+∠CHD+∠CDH=270°.

故∠BHC+∠CHD=135°，从而∠BHD=135°.

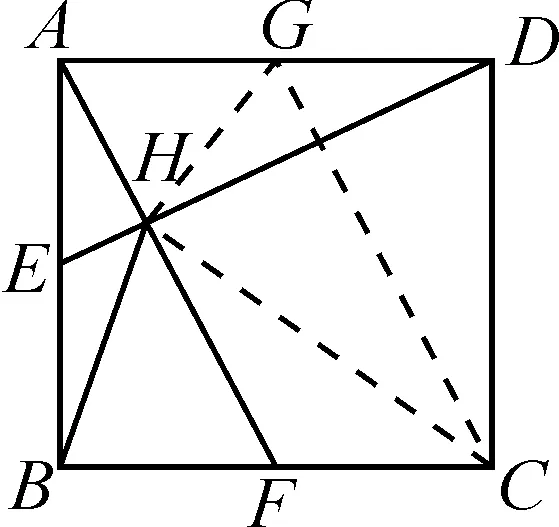
图3

解法2：如图3，取AD的中点G，连接HG，GC.

易证△ABF≌△CDG.

于是AF=GC.又因AG=FC，所以四边形AGCF为平行四边形，则AF∥GC.

由(1)知AF⊥DE，则GC⊥ED.

又易得HG=DG,所以GC是线段HD的垂直平分线，故HC=DC=BC.

故∠CBH=∠BHC，∠CHD=∠CDH.

因为∠BCD+∠CDH+∠DHB+∠CBH=360°，

所以∠CDH+∠DHB+∠CBH=270°.

即∠CBH+∠BHC+∠CHD+∠CDH=270°.

故∠BHC+∠CHD=135°，从而∠BHD=135°.

策略二:利用四点共圆来找到已知角和未知角的关系，从而到达事半功倍的效果.

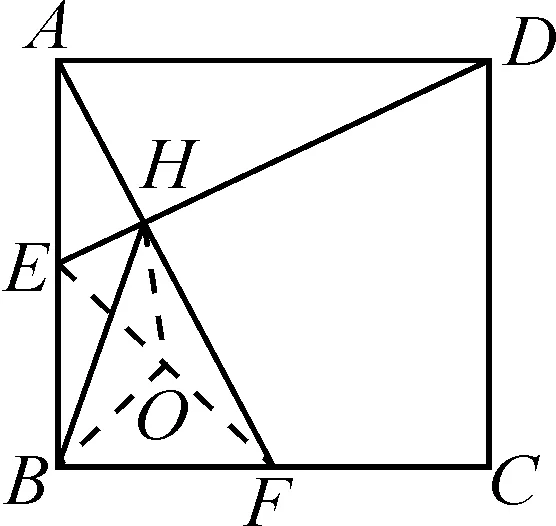
图4

解法3：如图4，连接EF，取EF的中点O，连接BO，HO.

因为△BEF为等腰直角三角形，△EHF为直角三角形，所以BO=HO=OF.

即点B，H，F在以O为圆心OB为半径的圆上.

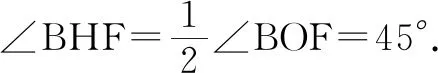
易得∠BHD=∠BHF+∠FHD=135°,即∠BHD=135°.

图5

解法4：如图5，延长AF至点M，使得FM=AF，连接CM，HC.易证△ABF≌△MCF，则∠BCM=90°.

所以点D，C，M共线，且AB=MC=DC,则点C为DM的中点.

由(1)知AF⊥DE，即∠MHD=90°.

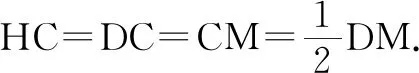
由DC=BC，得HC=BC.

由DC=BC=HC=CM，得点D，H，B，M在以点C为圆心，以CD为半径的圆上.

因为∠BCD=90°，所以优弧BD所对的圆心角为270°,进而∠BHD=135°.

图6

解法5:如图6，由(1)知AF⊥DE，即∠EHF=90°.

又由∠ABC=90°，可得

∠ABC+∠EHF=180°.

所以四边形BEHF对角互补.

因此B，E，H，F四点共圆.

于是∠BHF=∠BEF=45°.

故∠BHD=135°.

策略三:由第(1)问可知，AF与DE垂直，所以∠FHD=90°，所以求解∠BHD可转化为求解∠BHF；利用∠BHD与∠EHB的互补关系，亦可将问题转化为求∠EHB.而求∠BHF或∠EHB可以放到等腰直角三角形或者正方形中.

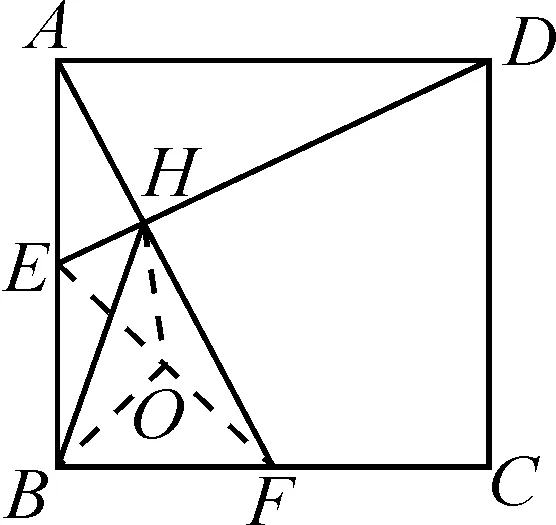
图7

解法6：如图7，连接EF，取EF的中点O，连接BO，HO.

由△EBF为等腰直角三角形，△EHF为直角三角形，得BO=HO=EO=OF，△BOF为等腰直角三角形.

所以∠OBH=∠OHB，∠OHF=∠OFH，∠OBF+∠OFB=90°.

又因为∠BHF+∠HBF+∠HFB=180°，所以可得2∠OHB+2∠OHF+∠OBF+∠OFB=180°.

所以∠OHB+∠OHF=45°，即∠BHF=45°，∠BHD=∠BHF+∠FHD=135°.

故∠BHD=135°.

解法7：如图8，作BM∥AF，HM⊥BM，BN⊥AF.易证四边形BMHN为矩形，△AHE≌△BNF，△BME≌△AHE.

故BM=AH=BN，即四边形BMHN为正方形.

由∠BHF=∠BHE=45°，得

∠BHD=∠BHF+∠FHD=135°.

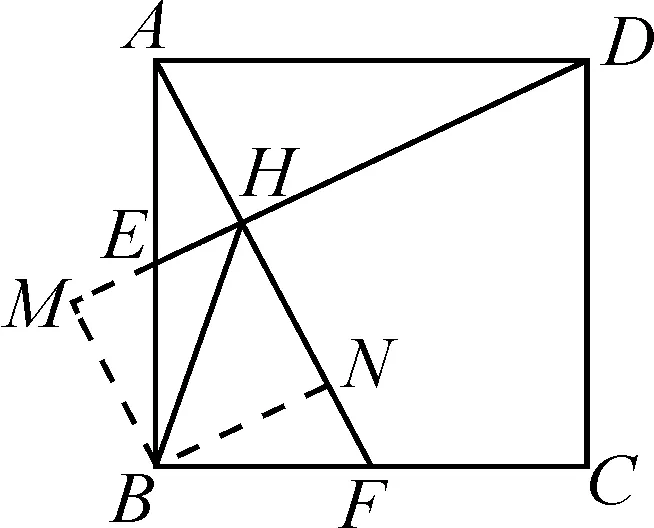
图8

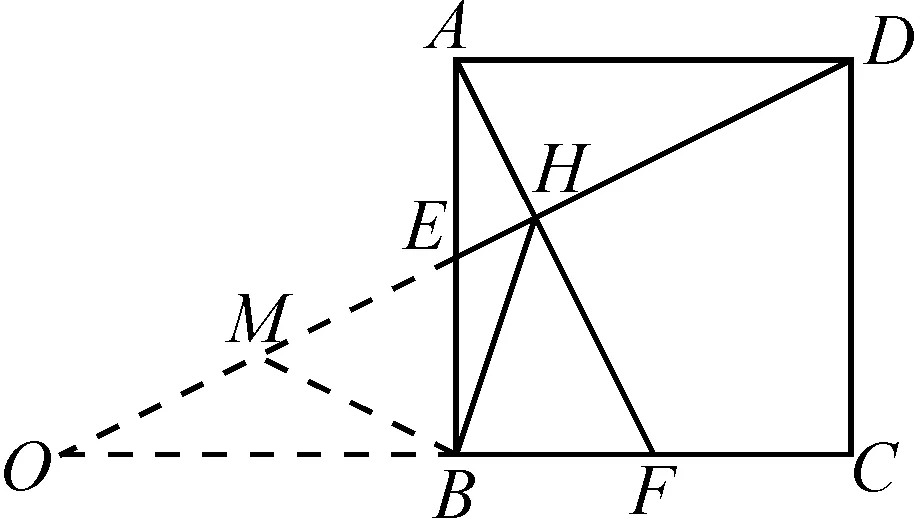
图9

解法8：如图9，延长DE，CB交于点O，作MB⊥HB交DE延长线于点M.易证△OBE≌△DAE，△OBM≌△ABH，△MBH为等腰直角三角形.

故∠MHB=45°，即∠BHD=135°.

图10

解法9：如图10，作BQ⊥HB交AF的延长线于点Q.

由∠HBQ=90°，可得

∠HBF+∠FBQ=90°.

又∠ABC=90°，则有

∠HBF+∠ABH=90°，

∠ABC+∠EHF=180°.

所以∠ABH=∠FBQ，∠BEH+∠BFH=180°.

又因为∠BFQ+∠BFH=180°，所以可得

∠BEH=∠BFQ.

又因为BF=BE，所以△EHB≌△FQB.

于是BQ=BH，即△BHQ为等腰直角三角形.

所以∠BHQ=45°.

故∠BHD=∠BHF+∠FHD=135°.

4 结语

本题可以从特殊的三角形、四边形相关知识、四点共圆、图形的运动等方面进行思考，此外，亦可用坐标、向量、三角函数等方法.题目的多角度思考大大激发了学生的发散性思维.在教学中，适当地对问题进行延伸、拓展，可以拓宽知识点间的横向联系，可以加深学生对知识的纵向认识，从而变孤立题目或单个题目的教学为对一类问题的学习．

一个问题可能有多种解法，我们要学会从多角度来思考问题、分析问题、解决问题，做到融会贯通，举一反三．解题教学要立足课标、教材，关注核心知识、基本图形，加深对图形结构的理解，加深对数学本质的理解，加强思维引导.在过程性教学中发展学生的探究意识，使得解法自然生成，真正将知识落到实处.引导学生结合题目的特点一题多解，一题多变，拓宽思路，帮助学生在变式训练中发展思维的灵活性与发散性，提升解题能力，培养数学洞察力，引领并促进数学核心素养在平时的教学中落地生根．