一种基于肌声信号的穿戴式助力系统运动意图检测算法
董 为 石永军 林玮琪
(哈尔滨工业大学机器人技术与系统国家重点实验室, 哈尔滨 150001)
1 引言
随着人类航天技术的不断发展,航天员出舱进行深空探测作业的次数会逐渐增多[1]。 在未来的航天活动中,航天员需要携带更多的科学仪器,穿越复杂的地形地貌,应对多种复杂恶劣的太空环境,这对航天员的运动能力提出了新的挑战[2]。
运动能力是航天员舱外作业重要保障。 当前的航天服具备生命安全保障和作业能力保障两大类功能,它们在具体实现上存在相互制约关系。其中,压力服的应用使其活动功效被明显削弱,实际表现为运动阻力增大、动作范围受限、灵活性变差等[3]。
近年来,穿戴式智能机电技术的兴起为这一问题提供了新的解决思路[4]。 以辅助穿戴者运动为目标的穿戴式智能机电系统也称为穿戴式助力系统,融合了机电一体化、传感技术、人工智能、人机工程多学科的技术,能够增强穿戴者的负载、机动、感知、防护等能力,帮助航天员提高在各种工作环境下的工作效率[5]。
穿戴式助力系统的研究内容主要包括具备人机相容性的结构设计、面向人机交互的控制算法研究和基于人体信号的运动意图感知三大方向[6]。 3 个方向的研究相辅相成,各国研究人员的相关成果也各有侧重,Ding 等[7]团队采用鲍登线等柔性单元实现了助力系统的柔性动力传递,极大地增加了人机系统的相容性;Xiloyannis 等[8]根据人体肘关节屈曲角度和助力电机回转角度间的关系建立起了对应的运动学模型,进而提出了肘关节重力补偿算法;Lessard 等[9]参考了康复治疗中的镜像疗法,在穿戴者一侧手臂的大臂和前臂处布置惯性测量单元,为另一侧手臂的助力提供参考输入。
在人体运动意图感知方面,常用的方法为借助助力系统上搭载的各类传感设备采集穿戴者当前的生理、运动信号,将采集到的信号通过特定算法处理后,建立起信号与运动间的映射关系,并由此辨识出穿戴者当前的运动意图,辨识的快速和准确与否,直接决定了助力系统的助力效果,是穿戴式助力系统研究内容的重要环节[10-11]。 在运动信号的选取上,表面肌电信号应用的最为广泛,代表性成果为Kawamoto 等[12]推出的HAL-5 型外骨骼机器人;Varghese 等[13]基于人体肩关节的逆运动学模型,借助神经网络技术,利用图像捕捉的方法预测人体肩关节的运动意图;Wang 等[14]推出的MINDWALKER 则采用了非侵入式脑电信号作为助力系统的参考输入信号;黄海等[15]研制的HEXO 外骨骼则通过采集人机间的交互力来辨识人体的运动意图。
从实际应用的角度来看,表面肌电信号对皮肤表面质量要求较高且易受环境电磁干扰,图像捕捉技术由于其外置传感器的特性故其使用场地受到限制[16],脑电信号受限于人脑的复杂性难以辨识出精确的运动动作,人机交互力信号从产生原理上已滞后于人体的运动,在快速性上有一定的欠缺[17]。
针对上述问题,本文提出了一种基于肌声信号的人体运动意图辨识算法。 肌声信号是由对应肌肉的振动产生,利用惯性测量单元采集后进行滤波与特征提取,最后利用机器学习的方法建立关节力矩与肌声信号间的映射关系,从而实现人体运动意图的辨识,最终通过试验验证算法的有效性。
2 肌声信号的采集与处理
肌声信号(Mechanomyogram,MMG),又称肌音信号、肌动信号,是肌肉轴向收缩时相互间的滑动摩擦产生的一种压力波。 在人体皮肤表面采集到的肌声信号是由多个肌纤维的不同步机械活动产生的复合信号,其中蕴含了参与本次运动的肌纤维的数目及其振动的振幅、频率等信息[6]。
肌声信号在肌力估计方面的应用已被证实具有可行性[18],且肌声信号相较于表面肌电信号,对传感器的要求较低,普通的加速度计即可胜任,信号的机械振动特性使得信号对传感器的安装位置较不敏感,偏离肌腹处[19]安装也可有较好的采集效果。 总的来看,肌声信号具有设备成本低、对摆放位置和皮肤表面条件的需求低、抗干扰性强等优势,是理想的人体运动意图辨识算法输入信号。
为获取肌声信号对应的肢体动作,本文采用九轴惯性测量单元(Inertial Measurement Unit,IMU)作为肌声信号的采集设备,以右臂肘关节屈曲伸展运动为例,试验选取了一名25 岁男性志愿者,无神经肌肉疾病史,将IMU 置于其右臂肱桡肌处,如图1 所示。
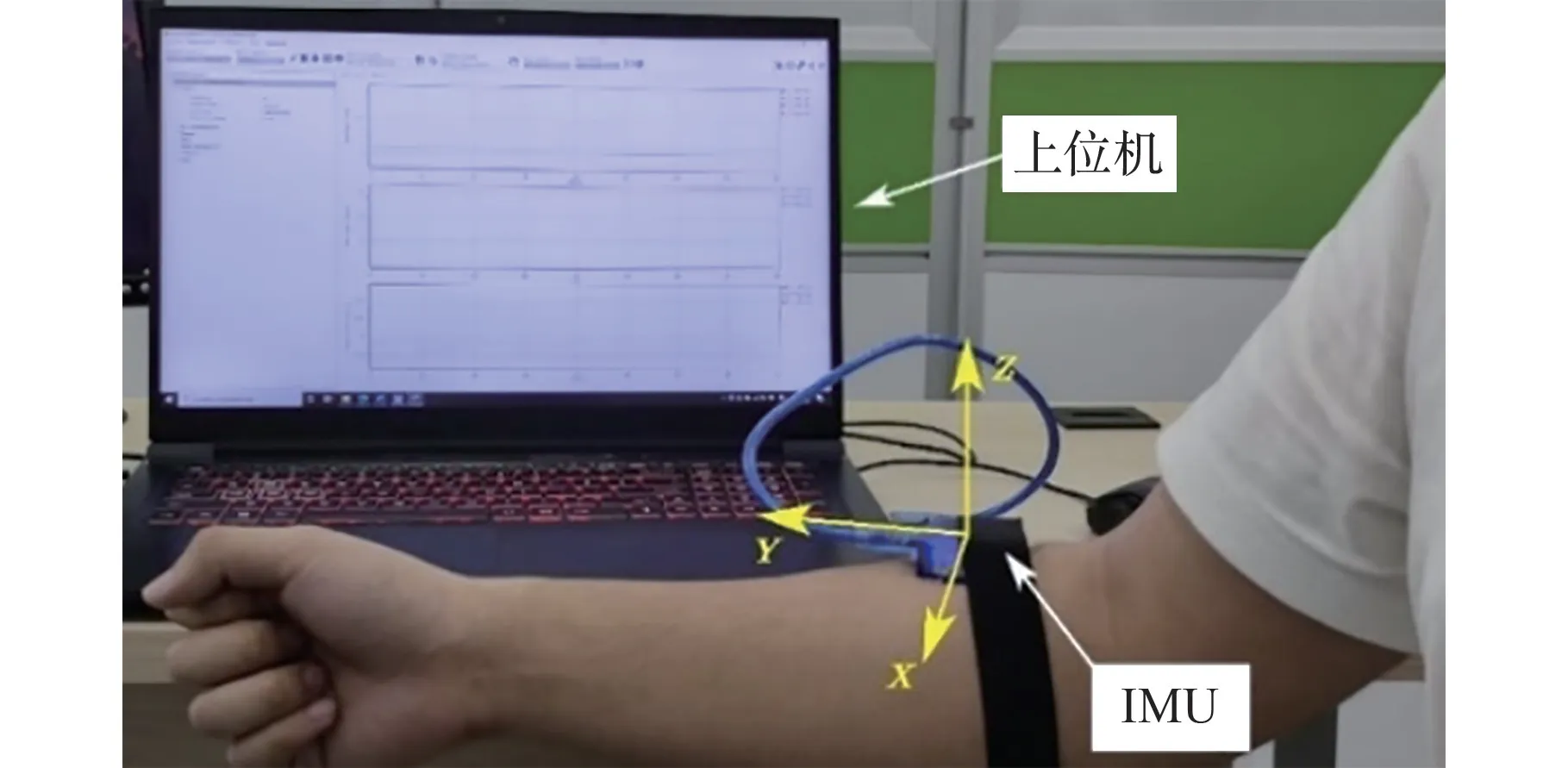
图1 肌声信号采样示意图Fig.1 Mechanomyogram sampling
为简化数据处理,同时不丢失可能的有效信息,对IMU 的三轴加速度计数据依照式 (1)进行降维。
式中,ACCx,ACCy,ACCz分别为IMU 的x,y和z轴加速度计读数,ACC为降维后的原始肌声信号。 令受试者右臂肘关节匀速完成一次屈曲伸展运动,采集到的原始肌声信号如图2 所示。

图2 右臂肘关节屈伸运动原始肌声信号Fig.2 Raw mechanomyogram of flexion and extension movement of elbow joint of right arm
可以看出,合成后的原始肌声信号里,蕴含着由传感器引入的高频白噪声和由肢体运动及重力加速度引起的低频运动伪迹,这些不必要的干扰将会严重影响肌声信号的采集效果,需要设计相应的滤波器,在滤除高频噪声及运动伪迹的同时尽可能保留更多的肌声信号。
需要滤除的噪声主要分布在高频和低频段,由于不同关节不同肌肉震动的频率特性各有特点,常用的带通滤波器难以满足通用性的需求;传统的以傅里叶分析为基础的频域处理方法常用于处理有较强规律性的平稳信号,面对类似肌声信号的随机非平稳信号则表现不佳。 针对上述问题,出于提高所设计滤波器的跨肌肉适应性的考虑,本文选择希尔伯特-黄变换(Hilbert-Huang Transform,HHT)对肌声信号进行分析。
HHT 变换主要由经验模态分解(Empirical Mode Decomposition,EMD)和希尔伯特变换两部分组成。 EMD 算法基于原始信号自身的局部时间尺度,能够将信号按频率高低分解为有限阶本征模态函数(Intrinsic Mode Functions,IMFs)和一个残差。 通过分析各个IMF,能够分辨出其中有高频白噪声和运动伪迹所主导的IMF 并将其剔除,将剩余的IMF 重新组合便可得到滤除噪声后的相对纯净的肌声信号。
以图2 所示的原始肌声信号为例,对其进行EMD 分解,分解共获得了9 阶IMF 和1 阶残差,分解结果如图3 所示。
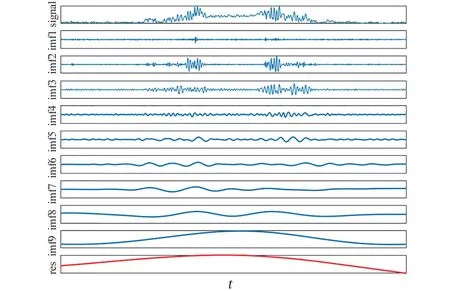
图3 原始肌声信号EMD 分解结果Fig.3 EMD decomposition results of raw mechanomyogram
对于随机白噪声,其随机性导致其各个时刻间的信号关联性较弱,及其自相关函数近似于零点附近的脉冲函数[20],为找出由噪声主导的IMF,引入自相关概念,自相关函数定义见式 (2)。
白噪声主要存在于高频段,故对分解出的前4 阶IMF 进行自相关求解并进行归一化处理,求解结果如图4 所示。 可以看出,第1 阶IMF 的自相关函数曲线符合白噪声的特点,将其视作噪声主导的IMF 剔除。

图4 前四阶IMF 自相关函数曲线Fig.4 Autocorrelation function of the first 4 IMFs
完成高频段噪声的滤波后,还需要进行低频噪声的辨识与滤除,参考文献[18]、[20]的研究成果,对于大多数被噪声污染的信号,其主要能量集中在低频段,越往高频段,其含有的能量越少,一定存在某阶IMF,使得该阶分量之后的IMF 为信号主导模态,该阶分量前的IMF 为噪声主导模态。
基于上述结论,做出如下变动:假设运动伪迹为求解的目标信号,肌声信号为高频噪声,则噪声与信号间一定会有一阶IMF 将两类模态区分开,引入IMF 的能量公式用于求解各阶IMF 的能量,能量公式如式 (3)所示。
式中,IMFi(j)表示第i阶IMF 的第j个信号值,n表示所包含信号值的总个数。
根据式 (3),求解出各阶IMF 所蕴含的能量,求解结果如图5 所示。 可以看出,第6 阶IMF之后的信号蕴含的能量较其他阶IMF 有显著的上升,故将第6 阶之后的IMF 视作由运动伪迹及重力加速度主导的IMF 并加以剔除,则至此完成了对原始肌声信号的高频和低频噪声的滤波,剩余的IMF2~IMF5 即为滤波后的肌声信号。
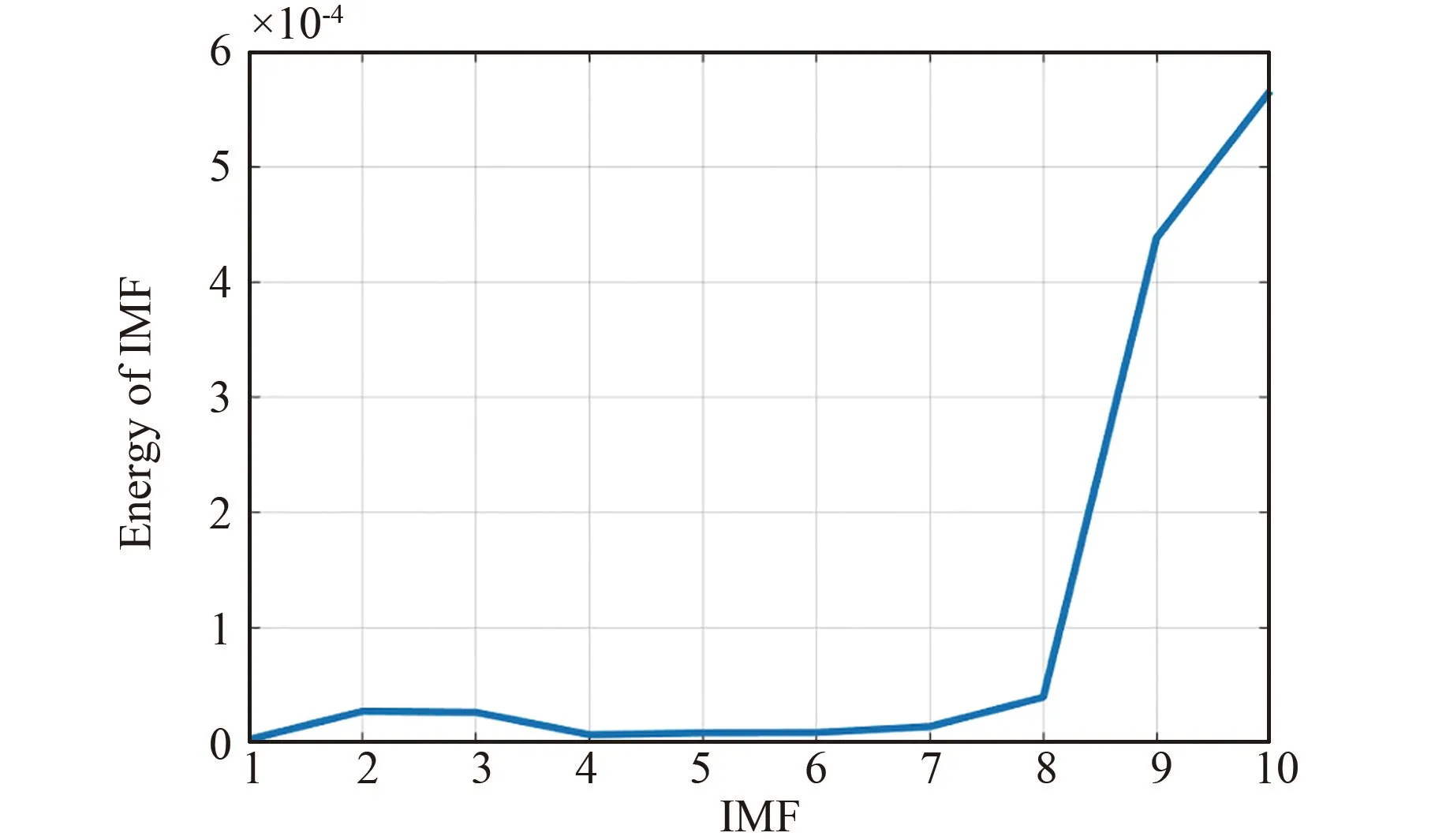
图5 各阶IMF 的能量曲线Fig.5 Energy curve of all IMFs
将剩余的IMF2~IMF5 重组,获得滤波后的肌声信号,与滤波前的肌声信号和对应右臂肘关节屈曲伸展运动的欧拉角对比如图6 所示。
由图6 可以看出,滤波后的肱桡肌肌声信号与对应肘关节的屈曲伸展运动间有十分清晰的对应关系,可将其用作人体运动意图辨识的输入信号。

图6 滤波前后肌声信号对比Fig.6 Mechanomyogram before and after filtering
3 肌声信号特征提取与关节力矩辨识
3.1 关节力矩信号的采集
人体的关节运动由对应的肌肉收缩产生,骨骼肌收缩使得肌腱拉动骨骼令关节产生运动,在一定程度上,可以通过辨识人体相应关节的关节力矩来表征人体的运动意图。
肌声信号与人体运动间有明确的对应关系,故可以通过设计算法建立起肌声信号与关节力矩间的映射关系来进行人体运动意图的辨识,以肘关节信号采集为例,搭建数据采集平台,如图7所示。

图7 肘关节数据采集Fig.7 Elbow data collection
人体肌肉收缩力难以通过非侵入的方式进行测量,且侵入式测量设备成本较高且易对受试者造成伤害。 针对此问题,本文设计了如式 (4)所示的矢状面下基于六维力传感器的关节力矩计算模型,模型示意图见图8。
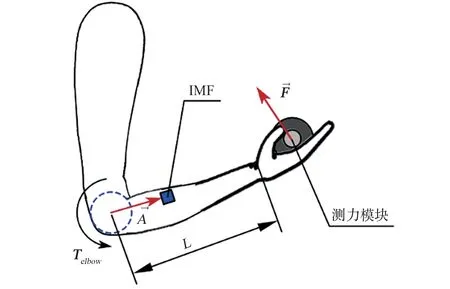
图8 关节力矩计算模型Fig.8 Joint torque calculation model
式中,A为人体前臂当前姿态向量,由绑缚于其上的IMU 测得,Fx、Fy、Fz为六维力传感器的x、y、z三轴读数,F为六维力传感器三轴读数的向量和,L为人体前臂长度。
基于关节力矩计算模型,采集受试者左臂肘关节力矩与左臂肱桡肌肌声信号,如图9 所示。
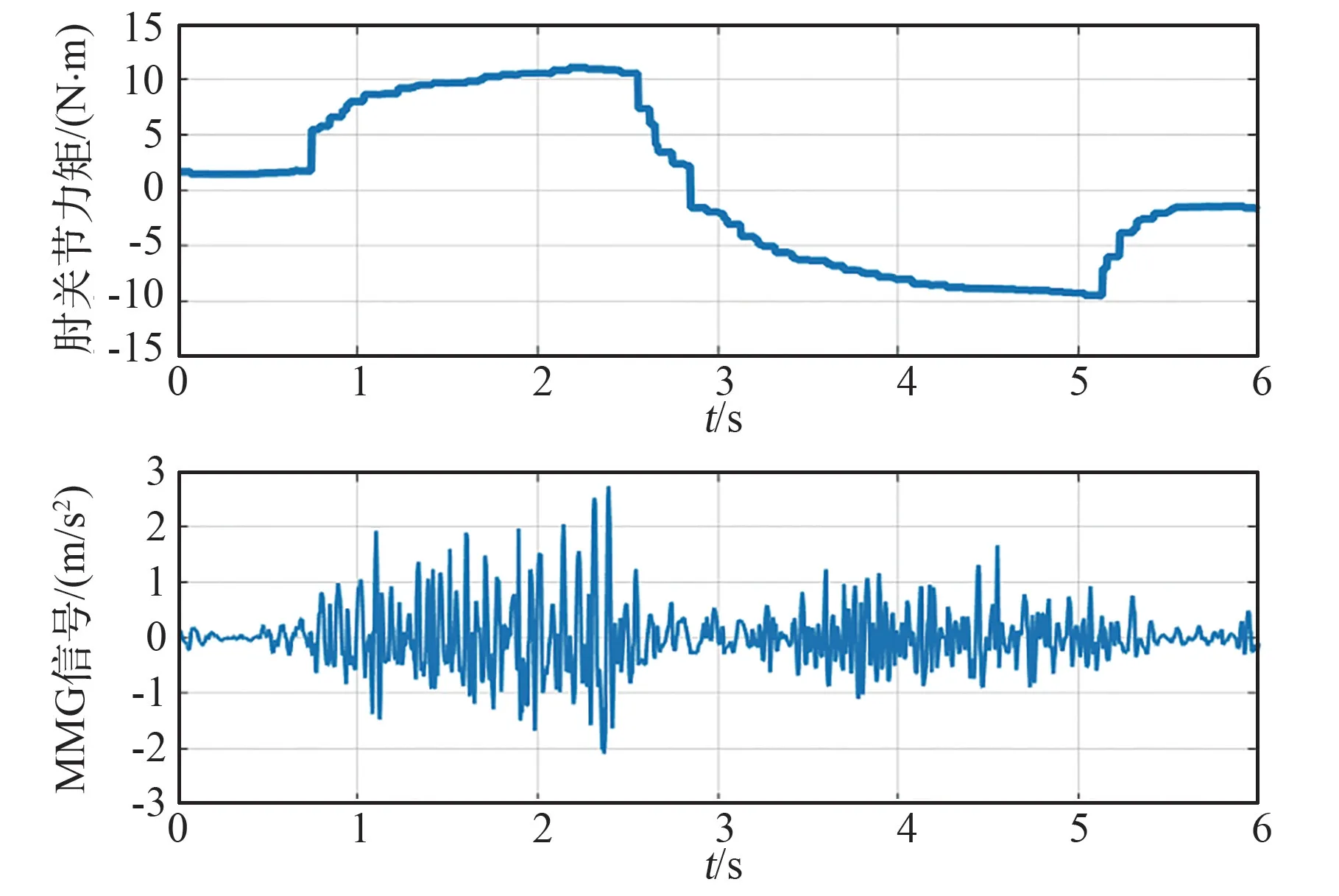
图9 左臂肱桡肌肌声信号与肘关节力矩对比Fig.9 Mechanomyogram of left brachioradialis andleft elbow torques
由图可知,肱桡肌肌声信号与肘关节关节力矩存在明显的对应关系,肘关节向屈曲方向出力时,肱桡肌肌声信号幅值较大;肘关节向伸展方向出力时,肱桡肌肌声信号幅值较小,因此可以仅使用肱桡肌处的肌声信号来估计肘关节的关节力矩。
3.2 肌声信号的特征提取
肌声信号是一种连续的时序信号,对其进行适当的特征值提取处理,既可简化运动意图识别算法,又可避免信息处理过程中有效信息的丢失。
通常认为人体主要通过2 种方式调节肌肉出力的大小:①通过调节当前参与出力的肌纤维数量,参与收缩的肌纤维数量越多,肌肉力量越大;②通过调整肌纤维的收缩频率来调节肌肉力量,肌纤维连续受到刺激后产生的收缩将会叠加,使收缩产生的肌肉力进一步增强。
基于上述原理,可以推导出如下结论:肌肉力量会伴随着肌纤维振动幅度和振动频率而变化,由此可以从时域、频域2 个角度对肌声信号展开分析,提取肌声信号的特征值。
由图9 可知,肌声信号的幅值与关节力矩间的相关关系角位明显,故以表征数据幅值有效值的均方根(Root Mean Square,RMS)作为肌声信号的时域特征,计算方法如式 (5)所示。
式中,Xi为第i个信号幅值,N表示采样个数。
频域方面,选取平均功率频率(Mean Power Frequency, MPF)作为频域特征值。 对采集到的肌声信号EMD 滤波后,进行希尔伯特变换并沿时间积分,即可获得表征信号频域与信号蕴含能量之间关系的希尔伯特边际谱,如图10 所示。
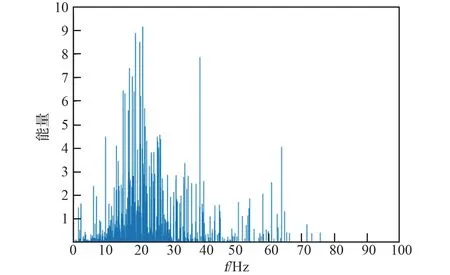
图10 希尔伯特边际谱Fig.10 Hilbert marginal spectrum
获得希尔伯特边际谱后,便可得知信号频率与信号能量间的对应关系,通过式 (6)即可计算出当前肌声信号的平均功率频率MPF。
式中,E为信号能量,f为信号频率。
肌肉力量可通过改变参与收缩的肌纤维数量来调节,即肌声信号中蕴含着参与工作的肌纤维的数量信息,故本文额外引入样本熵(Sample Entropy, SampEn)作为非线性方面的特征值,即通过度量信号中产生新模式的概率的大小来表征肌声信号中活跃的肌纤维数量。
此外,考虑到肌声信号在时间上的连续性,为了减少信息提取过程中的损失,同时兼顾系统计算能力,引入如图11 所示的滑窗法处理肌声信号,并设定窗口长度为500 ms,步进长度为50 ms。
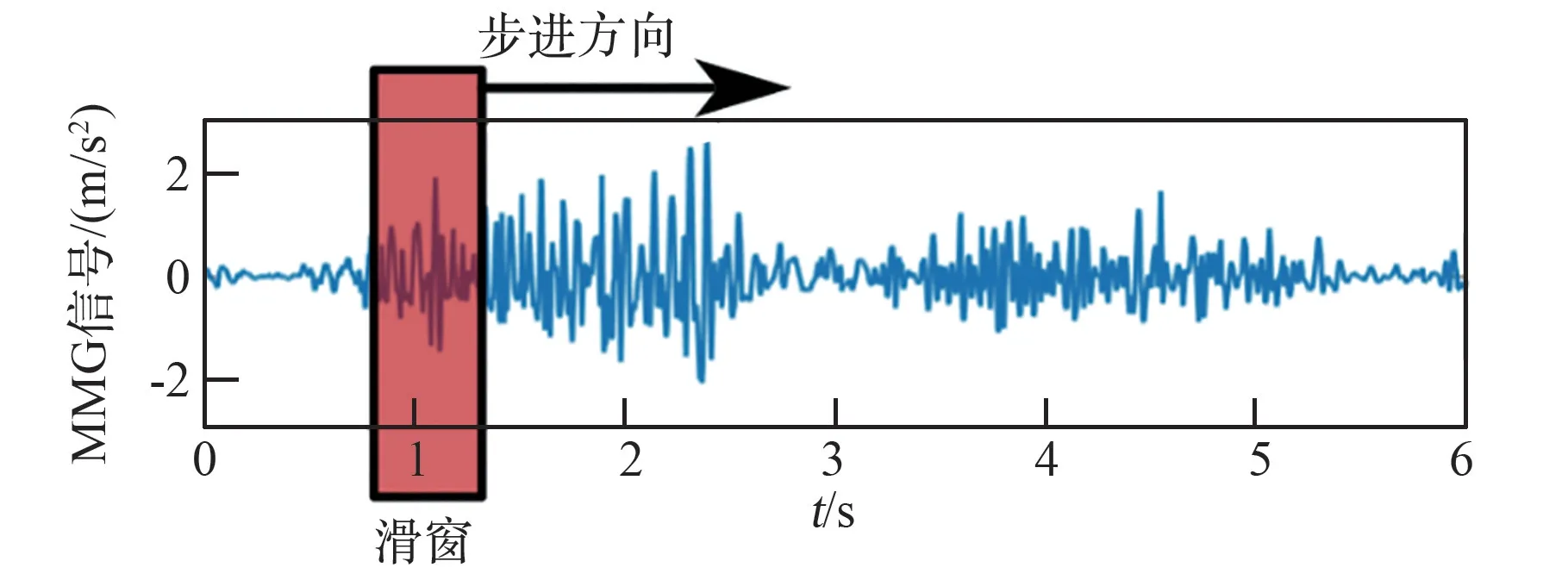
图11 滑窗法示意图Fig.11 Sliding window algorithm
3.3 基于机器学习的关节力矩辨识
受人体脂肪厚度,人体肌肉疲劳程度的影响,肌声信号与人体关节力矩间复杂的非线性关系难以利用传统的回归方法精确表述,故本文采用机器学习的方法,利用大量的测试数据来拟合肌声信号与关节力矩间真实的映射关系。
本文所述算法面向穿戴式助力设备,作为经典的人机交互系统,其助力安全性永远是应该优先考虑的事项,故选择随机森林回归模型作为关节力矩辨识的基础算法。
随机森林回归是一种属于装袋类型的继承算法,如图12 所示,模型由多棵分类回归树构成,每一棵回归树之间相互独立,互不影响,模型最终的输出由森林内的每一棵树共同决定。
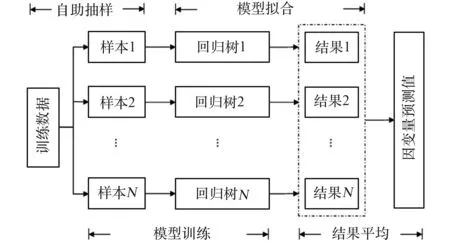
图12 随机森林回归模型Fig.12 Random forest regression model
随机森林回归模型具备极高的稳定性,只有在半数以上的回归树都做出错误预测的情况下,模型的输出才会严重偏离真实值。
4 试验与结果
4.1 受试者
征集3 名22~27 岁的男性志愿者,均身体健康,无神经及肌肉相关疾病史。
4.2 方法
1)模型训练与验证。 从中选择2 名受试者在如图7 所示的采集平台上分别完成左臂肘关节的屈曲伸展运动关节力矩及肌声信号特征值采集。 共采集到150 000 组样本数据,依据交叉验证的思想,抽取其中10 000 组数据作为验证集,其余数据作为训练集。 设定随机森林回归模型的子回归树数量为10,最小叶大小为1。
2)关节力矩辨识。 为验证本文所述算法的有效性,设计了关节力矩辨识试验。 3 位志愿者中,志愿者1 和志愿者2 参与了关节力矩辨识算法的训练数据集采集,志愿者3 未参与。参与训练集采集的志愿者的数据作为实验的试验组,将未参与采集的志愿者的数据作为试验的对照组。
试验以志愿者的肘关节运动为试验目标动作,试验数据由上位机直接采集并实时计算,设定测力平台六维力传感器的采样频率为200 Hz,控制系统关节力矩辨识频率为5 Hz。
试验开始前的24 小时内,志愿者被告知不要进行高强度的运动以避免肌肉的生理状态受到影响。 试验进行过程中,志愿者被要求以近似正弦波的出力方式对六维测力平台施加外力,施力的大小和频率则不做特殊要求。 每位志愿者需完成4 组实验数据的采集,每次数据采集至少持续30 s。 为防止肌肉疲劳产生的强直现象干扰试验结果,2 次试验间志愿者充分休息。
4.3 实验结果
1)模型训练与验证。 使用训练集离线训练出模型参数后,基于验证集对该模型的准确性进行评估,其交叉验证结果如图13 所示。 从中可以看出,通过力传感器测量和计算得到的关节力矩真实值,与通过模型获取的关节力矩预测值之间存在的差异较小。 说明离线训练效果达到了较好的水平,可用于后续的关节力矩辨识实验。

图13 交叉验证结果Fig.13 Results of cross validation
2)关节力矩辨识。 志愿者1 和志愿者2 的关节力矩辨识结果如图14 所示。 以力矩辨识结果的均方根差值(RMSE)和决定系数(R2)作为辨识效果的评价指标。 前者代表预测值和实际值之差的样本标准差;后者反映了回归关系在多大程度上可以解释因变量的变化,较高的值表明回归模型可以产生更好的预测结果。 可分别由式(7)和(8)计算。

图14 志愿者1 和志愿者2 的关节力矩辨识结果Fig.14 Recognition results of volunteer 1 and volunteer 2
式中,y^t,yt,分别表示力矩的预测值、实际值和平均值。
由实验采集的数据可得,志愿者1 关节力矩辨识结果的均方根差值为1.981 2,决定系数为0.953 2;志愿者2 关节力矩辨识结果的均方根差值为1.700 8,决定系数为0.862 0。
作为本次实验的对照组,志愿者3 的关节力矩辨识效果如图15 所示。

图15 志愿者3 的关节力矩辨识结果Fig.15 Recognition result of volunteer 3
志愿者3 的关节力矩辨识效果整体不太理想,均方根差值为3.426 1,决定系数为0.682 4。究其原因,不同志愿者间的体脂含量不同,脂肪对肌声信号传递起到的滤波作用不可忽视;且志愿者间的肌肉活性也各有差异,导致肌声信号存在个体差异。
综合来看,本文提出的基于肌声信号的人体关节力矩辨识技术在一定限度内有着良好的辨识效果。 由于不同人个体间的差异较大,该算法并不具备通用性,这种非通用性也能够类比到同一穿戴者的不同肌肉上,人体不同肌肉表现出的生理差异也十分显著,需要对每块目标肌肉单独采样,算法整体实现过程较为繁琐,有较大的改进空间。
5 结论
本研究主要是采集肌声信号和关节力矩来构成数据集,并离线训练随机森林回归模型从而建立其映射关系。 在验证算法有效性后,接下来便可以将训练好的模型导入助力装备的控制系统中进行力矩在线估计。 以肘关节屈伸动作为例说明了该算法的实施过程。 对于其他动作的力矩辨识,在流程上是类似的,但测量肌声信号的目标肌肉不同,故需要相应地单独训练模型参数。
1)提出了基于关节运动对应肌肉的肌声信号采集、滤波及特征提取方法,实现了人体运动意图信号的提取与分析。
2)提出了基于机器学习技术的肌肉肌声信号与人体关节力矩的映射方法,利用随机森林回归模型辨识人体关节运动的关节力矩,辨识决定系数可达0.9532,从而实现人体运动意图的辨识。

