水下训练服中性浮力姿态的一种量化测试方法

佘佳宏 张 磊 晁建刚 赵 维 林万洪

(中国航天员科研训练中心, 北京 100094)

1 引言

航天员执行出舱活动是空间站任务的重要组成部分。 为确保出舱活动任务的成功,航天员需在地面完成出舱活动任务训练。 模拟失重训练水槽可供航天员六自由度、长时间、无限制地连续训练,其原理是利用水的浮力平衡含航天员在内的水下训练服(简称服装)的重力,从而达到失重环境的效果模拟[1]。 在模拟失重训练水槽进行出舱任务训练前,需进行水下训练服的中性浮力配平。 潜水员首先调整服装的总活动配重块数量,使服装达到重力与浮力相等的状态,然后调整活动配重块在服装不同位置的分布,改变服装姿态。中性浮力配平后,水下训练服的姿态是模拟失重效果好坏的关键,一般称为中性浮力姿态。

空间站出舱活动任务中,由于作业点较多、作业操作复杂,需要不断变换操作姿态,与此相应,在模拟失重训练水槽训练时,考虑舱内和舱外的工作姿态不同、舱外行走和舱外作业的姿态不同,对水下训练服的姿态要求较高,姿态调节范围要求较大,包括水平位、前倾位和直立位等。 理想的姿态是航天员可以随意按需控制自身姿态,但实际上难以实现,只能寻求较好的配平姿态。 较好的服装配平姿态有利于失重环境的模拟,而较差的配平姿态则会影响航天员的操作和感受,使人感到像是不倒翁,改变自身姿态非常困难,导致水下训练的效率低、效果差。

仅靠目视进行服装姿态的定性评估,无法明确配平效果的好坏,这造成服装配平姿态没有统一的评价标准,不利于航天员训练时失重环境的模拟以及航天员失重环境训练和评价,因此需引入中性浮力姿态的量化指标。

本文在分析水下训练服姿态及其受力关系的基础上,总结出中性浮力姿态定量指标,提出一种测试方法,研制一套测试系统,并进行水下训练服测试。

2 姿态指标及其应用

水下训练服中性浮力姿态主要体现在2 个方面:中性浮力指标和姿态指标。 前者指重力和浮力的合力;后者指水下训练服俯仰、偏航、滚转3个欧拉角的大小以及重心和浮心间距。 水下训练服的欧拉角定义如下:在笛卡尔右手坐标系中,-x轴向为胸背向,-z轴向为头盆向,采用卡尔丹式欧拉角分类[2],绕x轴的旋转角度为滚转角,绕y轴的旋转角度为俯仰角,绕z轴的旋转角度为偏航角,滚转、偏航、俯仰皆为0°时,水下训练服为直立姿态,且左右受力平衡。

水下训练服欧拉角的大小由水下训练服浮心和重心的相对空间位置确定,欧拉角的改变由重心和浮心间距确定。 理想的中性浮力姿态是水下训练服重力和浮力的合力为零、重心和浮心完全重合。 实际上,理想中性浮力姿态在现实中无法实现,只能尽量接近[3]。

在水下训练服的使用过程中,应严格限制其上浮,以免发生安全事故,因此在进行中性浮力配平后,水下训练服会呈现轻微的负浮力(重力大于浮力),一般不大于0.5 kgf,相较于约240 kgf的水下训练服,可近似认为是中性浮力;同样,实际服装的重心和浮心无法绝对重合,则服装入水后必然稳定于某个确定的姿态。 因此,可以用3个参数来描述水下训练服的中性浮力姿态,分别是重力与浮力的合力、重心位置和浮心位置。 由于水下训练服的重心和浮心的位置难以精确测量,可以使用重力和浮力的合力、3 个自由欧拉角以及重心与浮心间距来描述。 这2 种描述中性浮力姿态的指标是等价的。

为提高试验训练效率,便于水下操作,实际上水下训练服的配重分布一般是左右对称,偏航、滚转欧拉角为定值,特别是当水下训练服的左右受力严格对称时,偏航、滚转的欧拉角为0°,因此实际操作中只需考虑水下训练服的俯仰角即可[4]。这样,水下训练服的中性浮力姿态指标可简化为重力和浮力的合力大小、自由俯仰角(无外力作用情况)、浮心与重心的间距。 这种简化方法的实质是将三维坐标下的重心和浮心关系简化为平面坐标关系。

水下训练服的中性浮力姿态指标见表1所示。

表1 的指标参数可用于定量判断服装模拟失重效果的好坏,较好的中性浮力姿态应是负浮力略大于零;重心和浮心间距接近于零(重心在下);自由俯仰角从直立位到头低位30°的范围内可调,便于作业点操作。

当航天员感觉自身中性浮力姿态配平效果差或试验训练指挥认为服装中性浮力姿态影响试验训练效率时,可对中性浮力姿态指标进行测试。另外,以上指标参数也可用于辅助指导水下训练服的中性浮力配平操作。 通过姿态测试,可将服装的重心和浮心间距反馈给潜水员,潜水员调整配重位置,将下方的活动配重块竖直移到上方,这样可使服装重心位置向上移动,且同时浮心位置基本不变,从而可缩短服装的重心和浮心间距,获得更优的失重模拟效果。

3 姿态测试方法

根据水下训练服的实际使用情况,针对表1 中简化后指标参数,水下训练服的负浮力可以直接通过水下拉力传感器测量得到。 对于自由俯仰角和重心与浮心间距,由于水下训练服外观复杂,无法直接测试,需通过测试其他参数,利用相互关系间接计算得到。 具体方法如下:对服装施加一定的力矩使其产生一定的俯仰角改变,只需知道外加力矩大小、方向和对应的俯仰角变化,就可得到如式(1)所示的力矩平衡方程:

式中,T为施加的力矩值,G为水下训练服的重力值,d为服装的重心和浮心间距,α为施加力矩后的俯仰角,α0为服装自由俯仰角。 服装俯仰角与重心和浮心间距的关系如图1 所示,图中F为水下训练服的浮力。

图1 服装俯仰角及重心和浮心变化示意图Fig.1 Illustration of relationship among pitch angle,center of gravity and floating center of the suit

对水下训练服施加一个已知力矩,并测出相应的俯仰角,可得到一组满足公式(1)的外加力矩-俯仰角数据,施加多个不同的力矩,得到多组不同的外加力矩-俯仰角数据。 由公式(1)可知:外加力矩和俯仰角是正弦关系。 将得到的多组数据进行正弦曲线拟合,得到拟合曲线公式,将该公式和公式(1)比对,则可计算出服装的自由俯仰角和重心与浮心间距。

4 测试系统

4.1 系统组成

根据第3 节测试方法,研制了一套中性浮力姿态测试系统,该系统包括岸上测控设备和水下测试机构,岸上测控设备和水下机构通过防水线缆连接,如图2 所示。

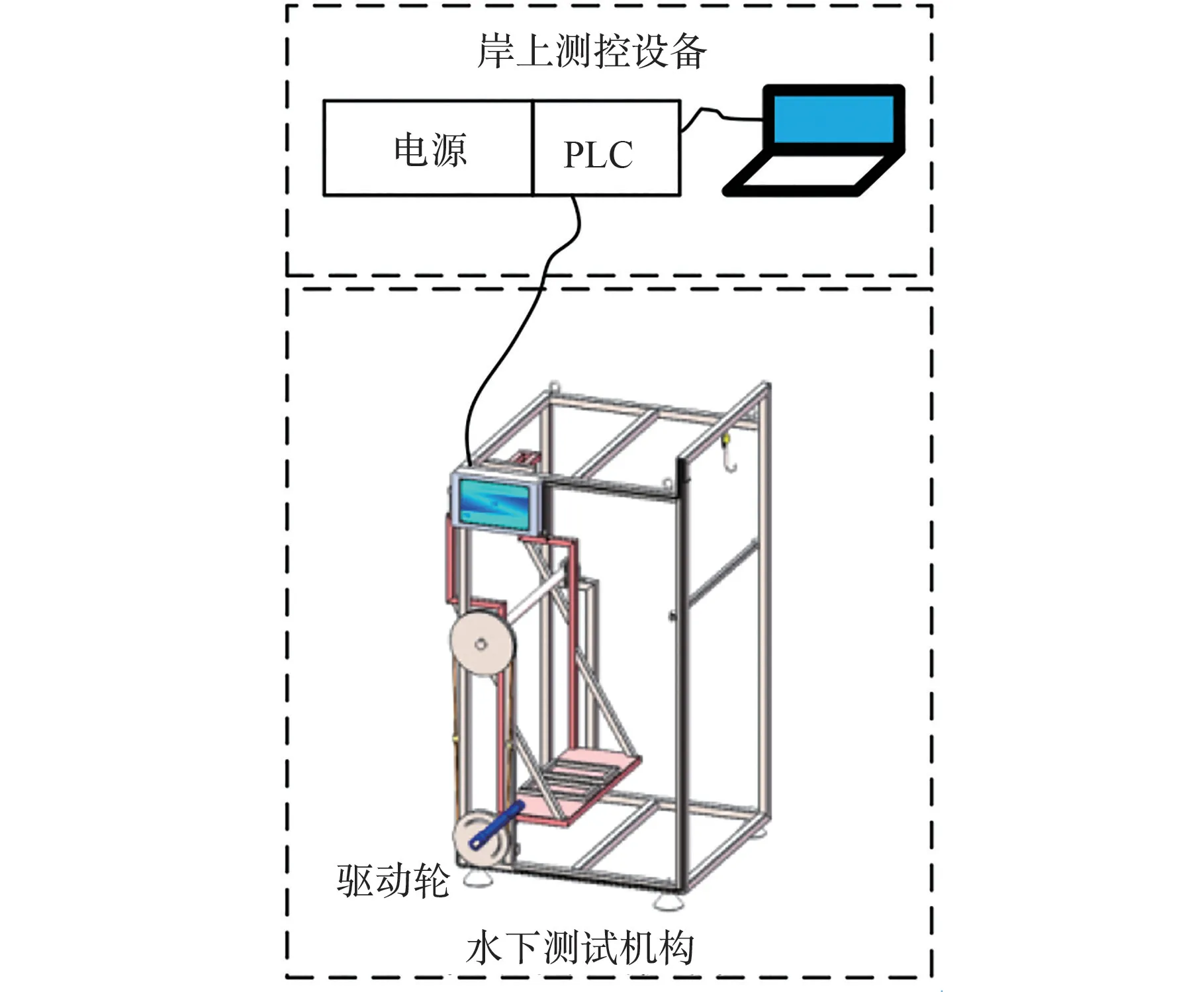
图2 中性浮力姿态测试系统示意图Fig.2 Illustration of neutral buoyancy posture test system

4.2 岸上测试设备

岸上测试设备由供电电源、数据采集PLC 主机(下位机)、测控笔记本(上位机)等组成。 下位机配置变量输入模块,上位机配置数据采集及分析软件。

4.3 水下测试机构

水下测试机构由框架、可转动支架、传感器等组成,传感器包括3 个拉力传感器和1 个转动角度传感器。 其中的1 个拉力传感器独立放置,用于测量负浮力大小;另2 个拉力传感器分别放置在转动支架驱动轮的两侧, 驱动轮半径为16.5 cm,这2 个拉力传感器数据乘以驱动轮半径,即可得到外加力矩。 俯仰角度通过角度传感器直接读出,记转动支架垂直于水平面时的俯仰角为0°,图2 中驱动轮逆时针转动为正。

4.4 测试内容

1)正常性测试。 水下测试机构入水固定后,将其和岸上测控系统连接,通电运行,检查各传感器数据是否正常,检查数据传输是否正常。

2)负浮力测试。 将水下训练服悬挂到负浮力测试拉力传感器下方的挂钩上,待传感器数据稳定后,通过读数得到负浮力测试结果。

3)空载测试。 考虑转动支架的重心和浮心不重合,存在转动支架的空载力矩,需测试出该转动支架的俯仰角-力矩关系,这样在实际测试水下训练服中性浮力姿态时,只需减去转动支架在该角度时对应的力矩,即可消除系统自身的影响,得到有效的外加力矩。 测试步骤如下:①水下转动支架空载时,潜水员在驱动轮的左右两侧分别依次增加配重,待转动停止并稳定后(利用角度传感器读数是否稳定来判断,下同),得到空载时转动支架的俯仰角和对应的施力大小;②根据驱动轮的半径,可知俯仰角对应的外加力矩的大小,记为T空载(α)。

5 测试系统验证

5.1 参考模型与仿真计算

为验证该测试系统是否准确有效,设计了中性浮力状态的参考模型,如图3 所示。

图3 参考模型设计示意图Fig.3 Illustration of reference model

该参考模型主要用来评估中性浮力测试系统的有效性和精度,可看成是水下训练服的模拟。由于参考模型设计为中性浮力,且模型所用材料、加工方式明确,模型尺寸可测,因此通过理论仿真计算出该模型的自由俯仰角和重心浮心间距。 将理论仿真计算结果与实测结果比对,即可评估中性浮力测试系统的功能和性能。

首先计算模型各组成部分的重力、重心和浮力、浮心,再通过组合的方式,计算出其整体重力(浮力)和整体重心、浮心[5],并通过重心和浮心的空间位置,计算出其重心、浮心间距和自由俯仰角。 结果如下:模型质量为23.1 kg;重心和浮心间距为21.53 cm,自由俯仰角为6.31°。

5.2 空载力矩测试

空载测试结果见表2。

表2 空载测试数据Table 2 Test data of no-load situation

根据表2 结果,可得到俯仰角-力矩的平面点图,由于转动支架的俯仰角、外加力矩满足正弦关系,因此用正弦曲线拟合方法给出对应的参数,拟合公式选择y=asin(x-b)+c,其中a、b分别对应公式(1)的G·d和α0,c为系统测试误差项。a、b和c初始值分别选择5000、1.0 和1.0。 利用基于MATLAB curvefiting 工具箱的非线性最小二乘算法Levenberg-Marquard 算法进行拟合[6],得到拟合公式(2):

5.3 参考模型测试

将参考模型安装到水下转动支架上,在驱动轮的左右两侧分别依次增加配重,记录配重数据和对应的姿态俯仰角,得到模型俯仰角对应的力矩大小,记为T实测模型(α),减去相应α角的空载力矩T空载(α),则可得到模型俯仰角和转动力矩的对应数据T有效模型(α),如公式(3)所示:

实际水下测试结果如下:负浮力为2.26 N。姿态测试结果见表3。

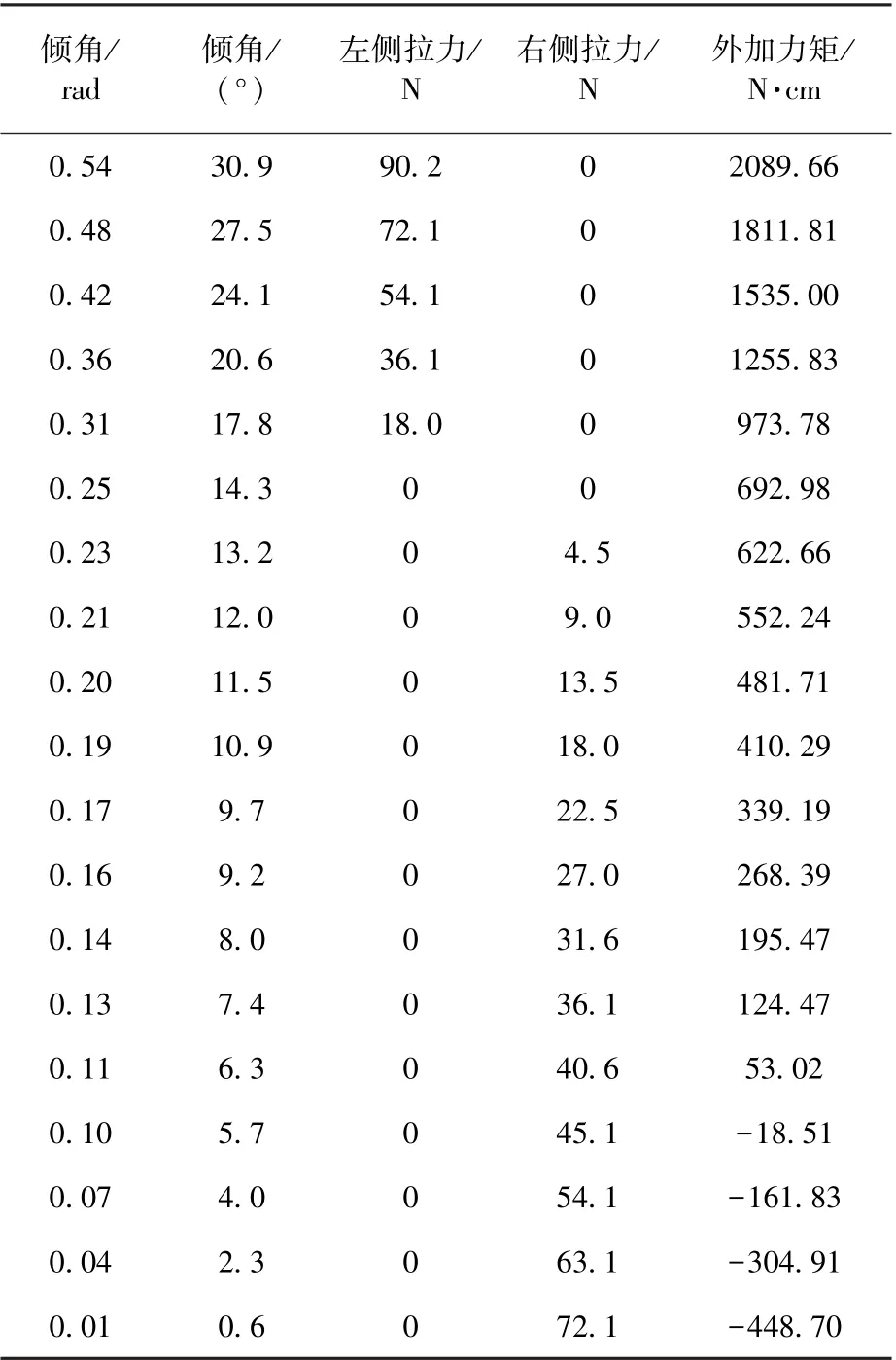
表3 参考模型测试数据Table 3 Test data of reference model

根据测试结果,采用正弦曲线拟合,选择公式y=asin(x-b),a和b初始值选择5000 和1.0。 选用Levenberg-Marquard 算法,得到拟合公式(4):

对照公式(1)可知:G·d=4885.0 N·cm,G=23.1 kgf,重力加速度取值为9.8 m/s2,可计算出模型的重心和浮心间距d=21.58 cm,自由俯仰角α0= 0.10 rad,即模型与铅垂线的自由俯仰角为5.88°。

5.4 测试系统准确度讨论

根据实验测试结果,重心浮心间距误差为0.05 cm,俯仰角误差为0.43°,可以看出服装姿态测试系统的设计是有效的。 误差原因包括理论仿真与实际的误差(如未考虑模型浮力块的吸水率、模型尺寸测量误差等)和测试系统本身误差(如拉力绳理想简化影响、转动摩擦影响等)。 后续为提高测试精度,需对模型重心和浮心位置进行实测,设计不同的参考模型(包括非左右对称模型)进行测试,对测试系统进行优化与改进等。

6 水下训练服测试

6.1 水下训练服测试步骤

水下训练服在入水前需测试出其总重量,在水下进行直立位中性浮力配平后,总重量减去因入水而额外增加的配重后,可得到服装配平后的总重量(和总浮力相同)[4]。

将水下训练服安装固定在水下转动支架上。由潜水员在驱动轮的左右两侧依次增加配重,记录配重数据和对应的姿态俯仰角,得到水下训练服俯仰角对应的力矩大小T实测服装(α),减去相应α角的空载力矩T空载(α),则可得到模型俯仰角和转动角度的对应数据T有效服装(α),如式(5)所示:

6.2 水下训练服01#实测

01#服装总质量为245.5 kg,负浮力为2.94 N。 01#服装姿态测试结果见表4。

表4 01#服装测试数据Table 4 Underwater test data of space suit 01#

对01#服装,得到拟合公式(6):

对照公式(1)可知:G·d=4555.0N·cm,G=245.5 kgf,重力加速度取值为9.8 m/s2,可计算出01#服装的重心和浮心间距d=1.89 cm。 自由俯仰角α0= 0.0252 rad,即服装与铅垂线的自由俯仰角为1.45°。

6.3 水下训练服02#实测

02#服装总质量为237.0 kg,负浮力为3.90 N。 02#服装姿态测试结果见表5。

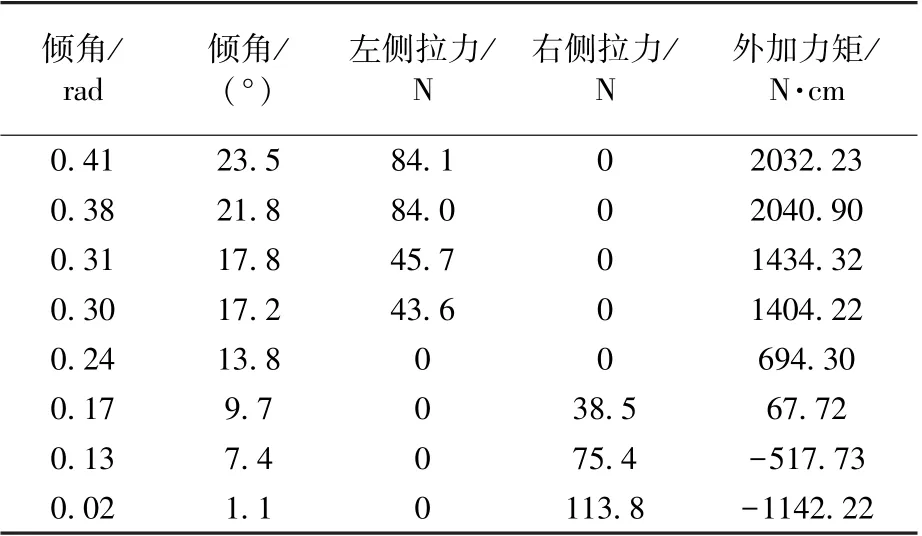
表5 02#服装测试数据Table 5 Underwater test data of space suit 02#

对02#服装,得到拟合公式(7):

对照公式(1)可知:G·d=9005.0 N·cm,G=237.0 kgf,重力加速度取值为9.8 m/s2,可计算出02#服装的重心和浮心间距d=3.88 cm。 自由俯仰角α0=0.1692 rad,即服装与铅垂线的自由俯仰角为9.7°。

图4 是空载、参考模型以及2 套水下训练服的实验测试情况,图5 给出了正弦曲线拟合结果。

图4 水下测试Fig.4 Underwater test

图5 拟合曲线图Fig.5 Curve fitting diagram of the test results

7 结论

1)从参考模型和水下训练服的测试结果来看,水下训练服姿态量化测试系统有效。 01#服装重心和浮心间距为1.89 cm,02#服装重心和浮心间距为3.88 cm,与水下表现符合;01#服装较容易改变俯仰姿态,02#服装则相对困难,这是因为较小的重心浮心间距,要求克服服装俯仰变化的力矩也相对较小。

2)本文采用的计算方法是正弦曲线拟合,要求采集的数据较多,有利之处是可提高测试精度,不利之处是由于每一组数据需在服装平衡稳定后才能读取,因此比较费时。 可考虑采用快速测试方法,即通过联立方程组的方式求解,只需获得2组数据即可,但相应的计算结果精度较低,只适用于需要快速测试的场合。

水下训练服中性浮力姿态测试进一步研究,需从以下方面不断完善:①增强水下训练服的自由姿态与测试系统的匹配性;②降低水下训练服四肢位置变化带来的影响;③克服外部条件(如脐带、水扰动)对测试结果的影响;④考虑服装左右非对称情况下的中性浮力姿态测试。