基于石墨烯圆盘的可调多带“葫芦形”超材料吸收器

晋 豪, 谢征微

(四川师范大学 物理与电子工程学院, 四川 成都 610101)

超材料是所谓的人工工程结构,它表现出许多天然材料不具备的、有趣的甚至反常的电磁特性,在完美透镜、超分辨率成像、负折射、高灵敏度传感器、偏振转换器、光学隐身等方面有着重要的应用[1-6].特别是近年来超材料在电磁波吸收领域的应用引起了人们的广泛关注.在Landy等于2008年首次报道了一种基于阻抗匹配原理,通过金属表面谐振结构的单频段完美超材料吸波器[6]后,人们又陆续提出了从微波、太赫兹、红外到光学频率的一系列超材料吸收器[6-10],但由金属构成的超材料吸波器有一个典型的缺陷,即工作频率和吸收率由原始结构固定,难以调谐[11].

石墨烯是一种二维超薄碳材料,由于其独特的力学、热学、光学、电学和门控可调特性,近年来备受关注.石墨烯材料的费米能级、电导率和载流子迁移率可以在THz和红外波段频率范围内通过控制偏置电压进行调制[12-14].利用该特性,人们提出了大量基于石墨烯的超材料可调谐的完美吸波器,这类吸收器的一个主要特点是在器件几何尺寸固定的情况下,通过外加偏压或化学掺杂实现吸收性能的可调,如Ke等[15]在2015年提出了十字架结构的可调石墨烯超材料吸收器,可实现太赫兹波段可调的单峰窄带吸收,并能通过调整十字架长度和宽度来调整吸收峰位置.Xiang等[16]在2018年提出了“L”型双带可调的石墨烯超材料吸收器,可实现太赫兹波段可调的双峰窄带完美吸收.Han等[17]在2021年提出了基于金属十字架结构的可调石墨烯超材料吸收器,实现吸收器从单峰到多峰的可调.此外,人们还研究了方环、盘、t形、椭圆环等石墨烯形状[18-21]产生的可调谐单频带、双频[13-14]、三频带[22-23]或宽带吸收[24-25].

目前已有的研究表明,石墨烯吸收器和石墨烯的表面几何构型有着重要的关系,不同的几何构型对应于不同频率的吸收.如何通过简单的几何构型实现单频到多频的吸收一直是石墨烯吸收器研究中人们所关注的问题.本文基于简单的石墨烯圆盘结构,通过不同半径石墨烯圆盘的叠加,提出了一种单频到多频且可调的石墨烯超材料吸收器.数值仿真结果显示,该石墨烯吸收器可实现双频几乎100%的完美吸收.通过外加偏压调谐费米能级,调整吸收器的结构参数和电磁波的偏振角,可以实现单频到多频的可调吸收.另外,在入射角很大的情况下,该吸收器也能保持较高的吸收率.因此,该超材料吸收器在传感器、信号检测或筛查等方面有潜在的应用前景.

1 结构设计

本文提出的超材料吸收器的单元结构由3层组成,如图1所示.该单元结构的最上层由半径分别为r1和r2的单层石墨烯圆盘重叠构成,结构周期P=5.4 μm,中间层为厚度t2=4.0 μm、介电常数为3.9的无损耗SiO2的介电材料层,底层为厚度t1=0.2 μm的金基底(导电率是4.56 ×107s/m),底部的金基底厚度足够厚,因而入射电磁波的透射率可近似为0[14].

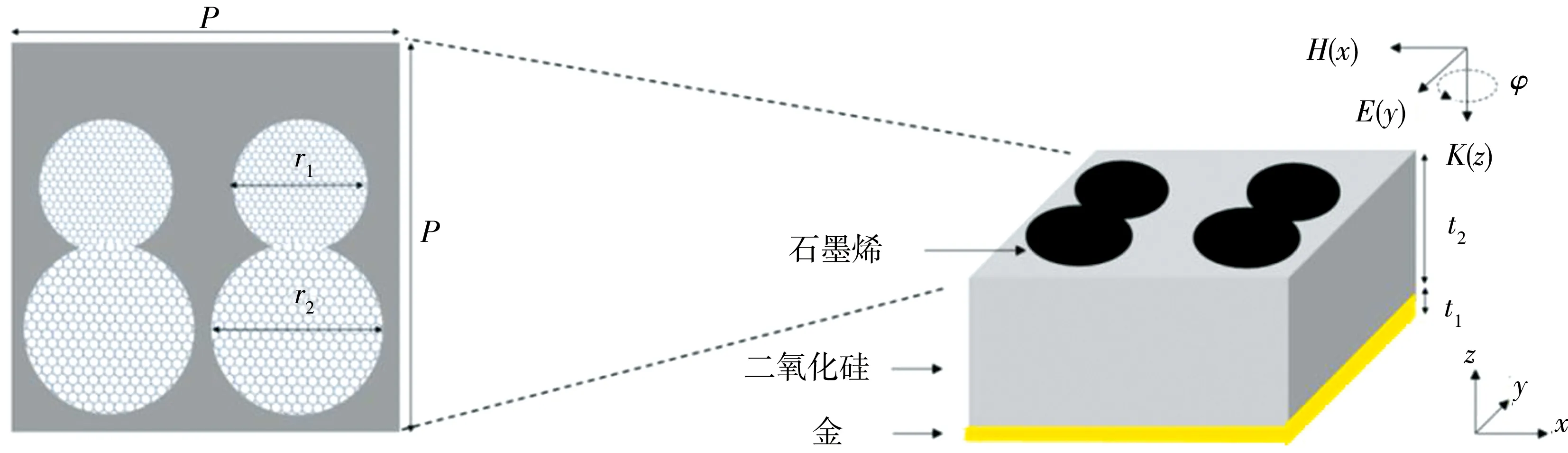
图 1 吸收器示意图

单层石墨烯的介电常数ε可由下式[22,26-27]得到

(1)

其中,d=0.334 nm为石墨烯层的厚度,Z0=377 ohm为自由空间阻抗,K0表示电磁波在自由空间中的波数[28],σgra为石墨烯的表面电导率[29]且定义[30]如下:

σgra=σintra+σinter,

(2)

σintra=

(3)

(4)

σintra和σinter是与带内和带间跃迁相关的电导率,e、T、kB和h分别代表电子的电荷、温度(T=300K)、玻尔兹曼常数和归一化普朗克常数,ω、τ和Ef分别表示外加交变电场的角频率、弛豫时间和费米能级.在THz频段内,带间贡献与带内贡献相比可忽略.因此,石墨烯层的电导率σgra可简化为如下Drude模型的形式[14-15,31]

(5)

由(5)式可以看到通过施加偏置电压和化学掺杂改变费米能级和弛豫时间调控表面电导,进而对吸收率实现调控[14].

本文都是基于电磁仿真软件CST进行的计算和模拟.通过CST仿真软件可得到S参数,然后求出吸收谱和空间相对阻抗.吸收率可由

A(ω)=1-R(ω)-T(ω)=

1-|S11|2-|S21|2

计算得出,其中A(ω)指吸收率,|S21|2是透射散射系数,反射系数

R(ω)=|S11|2.

因为底层金基底足够厚,所以透射系数[13,32]

T(ω)=|S21|2=0.

因此,吸收率公式可被简化为

A=1-|S11|2.

通过这个等式可以知道,要得到高的吸收率,唯一的方法就是减小反射系数.由表面阻抗理论,当吸收器等效阻抗与自由空间阻抗匹配时,反射系数最小,于是可通过控制结构参数来获得最佳阻抗匹配实现大的吸收率[14-15].

2 结果与讨论

2.1 不同的大小圆之间的圆心距对吸收的影响对于圆盘状石墨烯的吸收器可以调节的几何结构参数有石墨烯圆盘的半径、介质层厚度、每个单元的周期等.为简便起见,在整个结构几何尺寸优化过程中,介质层厚度和周期长度均保持固定值,分别为

t2=4.0 μm,P=5.4 μm,

石墨烯费米能级和弛豫时间设置为0.7 eV[33]和1.1 ps[31].

首先,对单个石墨烯圆盘吸收率随半径变化的吸收情况进行了模拟,如图2所示.结果显示,当圆盘半径r逐渐增大(从0.6 μm增大到1.4 μm)时,吸收峰频点从9.10 THz变化到6.94 THz,吸收峰向低频方向移动,有明显的红移[13,32],吸收率则从98.84%逐渐降低至90.08%.在r=0.6 μm,频率为9.10 THz,以及r=0.8 μm,频率为7.86 THz时,可以观察到吸收率分别为98.80%和93.10%的吸收峰[34].

接下来选取2种尺寸半径

r1=0.8,r2=0.6

的石墨烯圆盘,进一步对由这2种尺寸半径石墨烯圆盘组成的超材料吸收器(如图1所示)的吸收率进行仿真模拟.

首先计算了大圆与小圆的圆心距离d(从0.95 μm增大到1.45 μm)对吸收率的影响,如图3所示.可以看出,对应于不同的圆心距,吸收器具有单频和双频的吸收峰.当r1和r2圆心距d为1.25 μm时,在4.97 THz和8.97 THz对应的频率处,有2个吸收率分别高达99.99%和99.98%的完美吸收峰[14,34],此时的大圆r1与小圆r2相交,从外形上看就类似于“葫芦”.

图4为2个共振频率下所对应的电场强度分布.由相应的电场强度分布可知,高频吸收峰处的电场贡献主要来自大圆,而低频吸收峰处的电场贡献来自大圆和小圆[14],因而高频处的吸收主要由大圆贡献,低频处的吸收则与小圆和大圆贡献都有关系.在入射电磁波的电场作用下,石墨烯圆由于局域表面等离子共振,可以看作是一个偶极子,当2种尺寸的石墨烯圆盘结合时,由于偶极-偶极的相互作用,从而对石墨烯圆盘的电场分布以及吸收峰的位置和强度带来了影响[34-35].

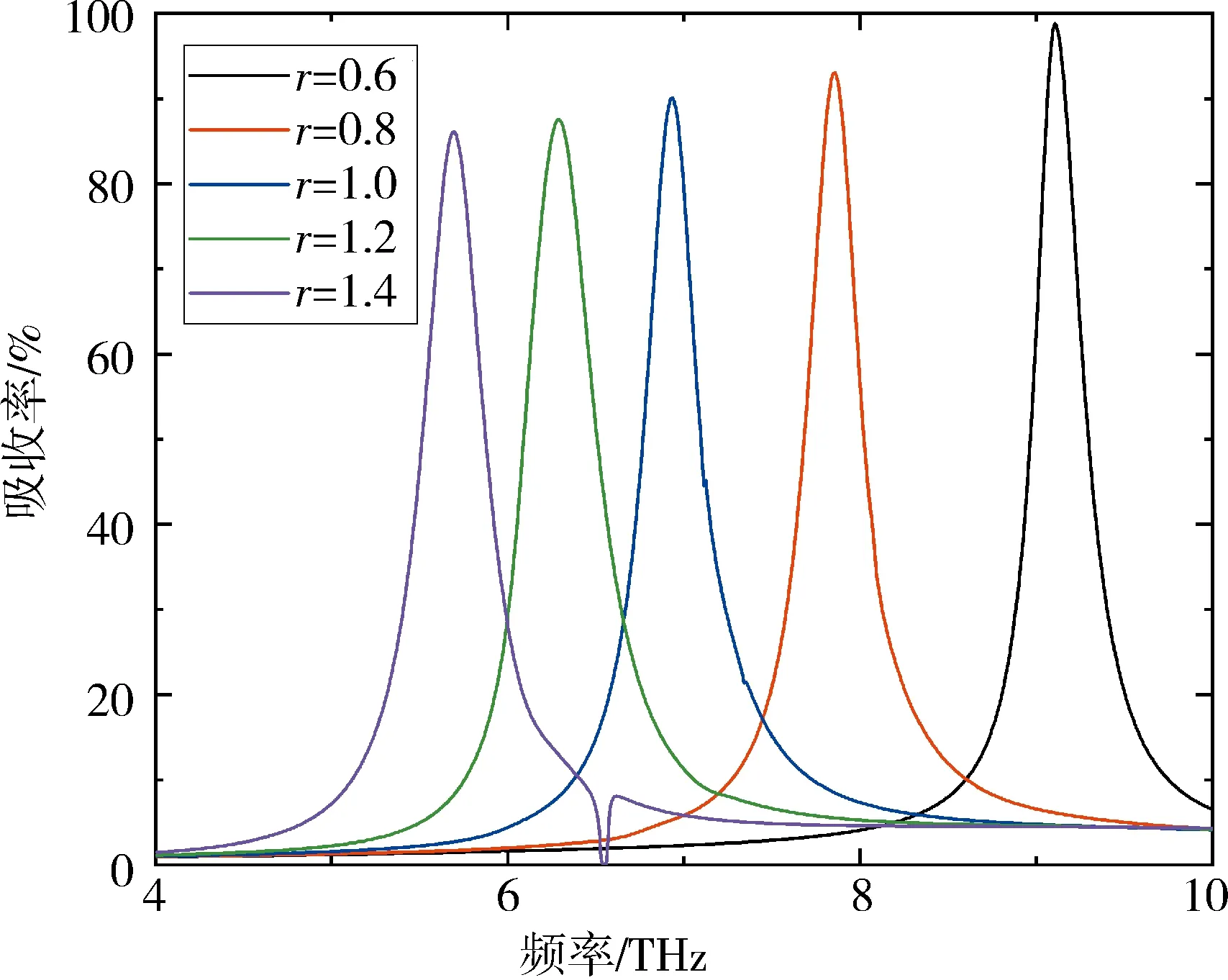
图 2 超材料吸收器在不同的圆半径r(从0.6 μm 到1.4 μm)下的吸收曲线

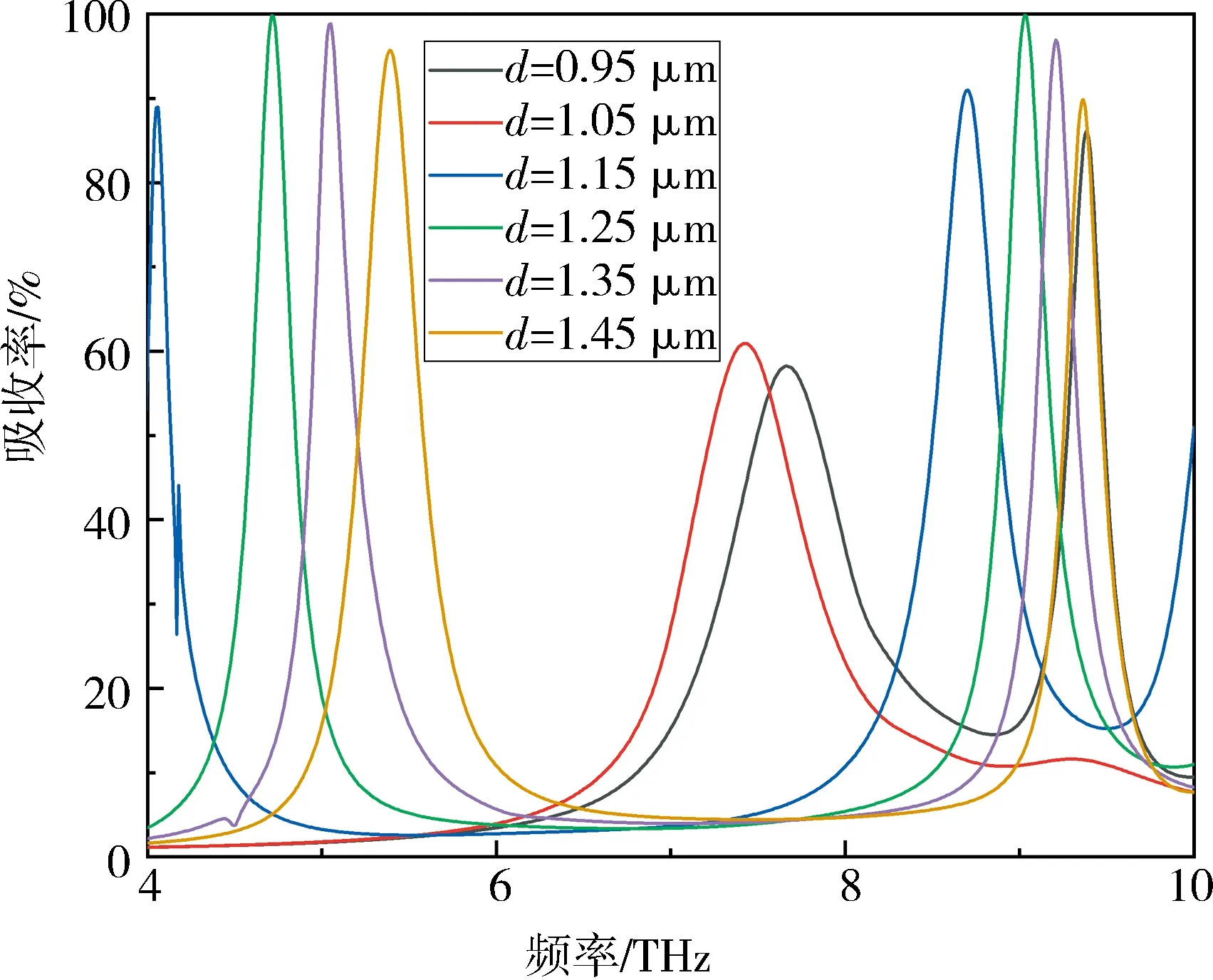
图 3 超材料吸收器在不同的r1与r2圆心距d(从0.95 μm到1.55 μm)的吸收曲线

2.2 不同的石墨烯费米能级对吸收的影响由石墨烯构成的超材料的吸收器的一个重要特点是可以通过外加偏压改变石墨烯中的费米能来对吸收性能进行调节.图5显示了所设计的“葫芦”状吸收器随费米能的变化，其中

d=1.25 μm,r1=0.8 μm,r2=0.6 μm.

可以看出,随着费米能的增加,吸收峰往高频移动[14,32].另外,在费米能Ef为0.5 eV和0.6 eV时,吸收器在频段内出现了3个吸收峰.图6给出了费米能为0.6 eV的电场分布图,可以看出,从低频到高频,3个吸收峰处的贡献分别主要来自大圆和小圆、大圆、小圆[14].

(a) T=4.36 THz (b) T=8.34 THz (c) T=9.82 THz

2.3 不同的石墨烯弛豫时间对吸收的影响在不改变几何参数的情况下,石墨烯层中弛豫时间对吸收性能的影响如图7所示(从0.4 ps到2.0 ps).在计算过程中费米能固定为

Ef=0.7eV.

结果表明,共振峰的频率随弛豫时间的变化保持不变,低频处为4.71THz,高频处为8.71THz,而吸收率随弛豫时间的增加先增大后减小[22,31].低频处的谐振峰吸收率,随着弛豫时间从0.4ps增加到2.0ps,吸收率由79.37%增加到99.79%,再降低到92.85%,调制深度定义为

高频处的谐振峰吸收率由77.00%提高到99.96%,然后降低至93.26%,调制深度为22.97%.

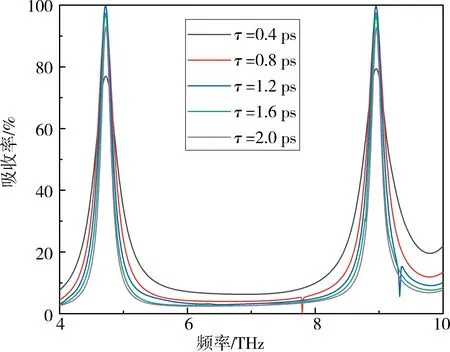
图 7 超材料吸收器在不同的弛豫时间下的吸收曲线

2.4 不同入射角对吸收的影响下面研究电磁波入射角度对吸收器吸收性能的影响(从0°到80°).对于TE模式,将入射光的入射角由沿Z轴负方向(θ=0°),按步长为20°逐渐改变入射光角度与Z轴负方向的夹角直到80°,其中

d=1.25 μm,r1=0.8 μm,r2=0.6 μm,

吸收光谱如图8所示.随着入射角θ的增大,吸收器在低频和高频处的吸收率均逐渐减小,且吸收峰的位置有较小的红移.在0°到60°内,变化入射角对吸收率的影响不大,都在90%左右.另外,由图9更清晰地展示了不同入射角下的吸收图像,该结果表明,设计的超材料吸收器在大的入射角情况下也能保持高的吸收率.

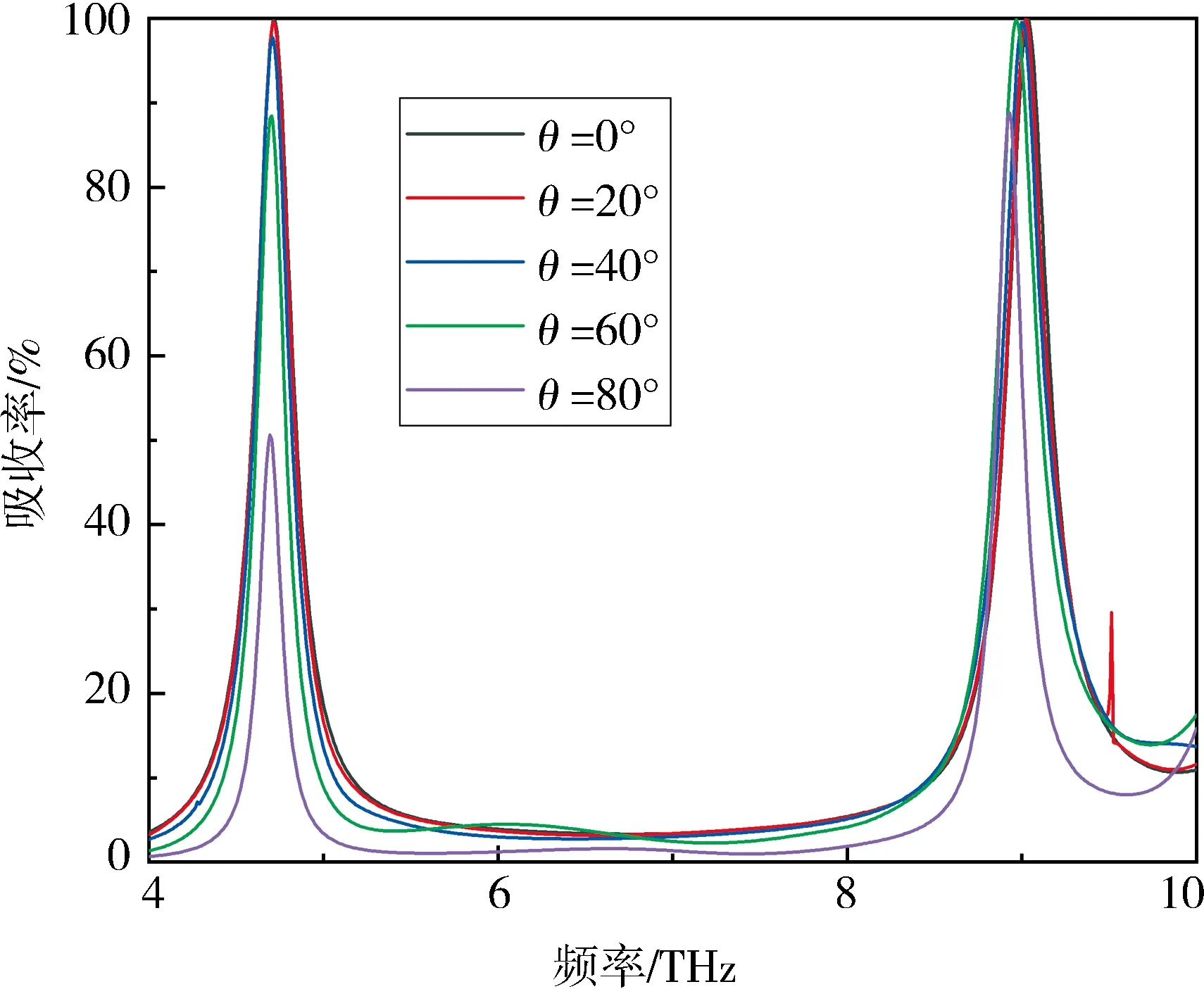
图 8 超材料吸收器在不同的入射角下的吸收曲线

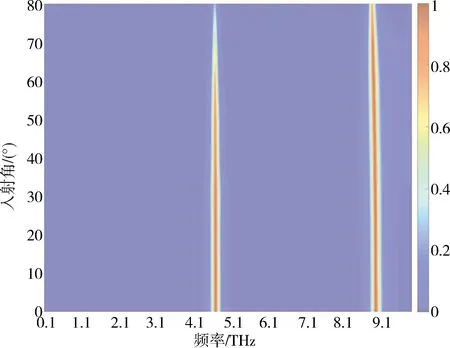
图 9 吸收器在石墨烯层的吸收谱

2.5 不同偏振角对吸收的影响下面研究偏振角φ对吸收器吸收性能的影响(从0°到90°).如图10所示,当入射电磁波的偏振角从0°旋转到90°时,随着偏振角的增大,超材料吸收器在低频处的吸收率逐渐减小,在高频处的吸收率先减小后增大(d=1.25 μm,r1=0.8 μm,r2=0.6 μm,参数如表1所示).低频处的吸收峰位置有轻微的蓝移,从4.71 THz变化到4.73 THz,吸收率从99.99%不断降低至0.05%,调制深度为99.95%.高频处的吸收峰位置则有较为明显的蓝移,从8.97 THz变化到9.33 THz,吸收率则从99.98%降低至4.78%,调制深度为95.22%,随着偏振角的变化,在频率为7.77 THz处出现了一个微小吸收峰,随着偏振角增大,吸收率逐渐从12.46%增大至70.10%.图11更清楚地展示了不同偏振角下的吸收图像.总的来说,通过旋转偏振角,可以实现单频到多频吸收的有效调节.

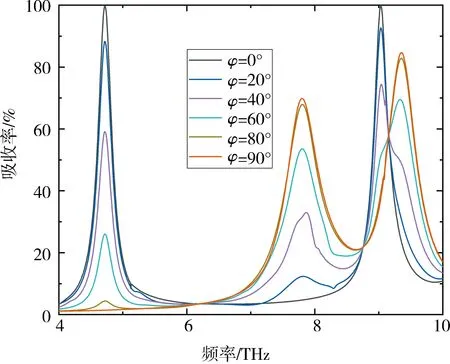
图 10 超材料吸收器在不同的偏振角下的吸收曲线

吸收曲线随偏振角的变化的原因是由于吸收器中存在2种半径大小的石墨烯圆盘,导致吸收器单元结构具有形状各向异性,随着偏振角的变化,石墨烯圆盘的耦合强弱也发生变化,从而影响了吸收峰的位置和吸收率大小.

表 1 不同偏振角时吸收峰最高值以及所对应的频点

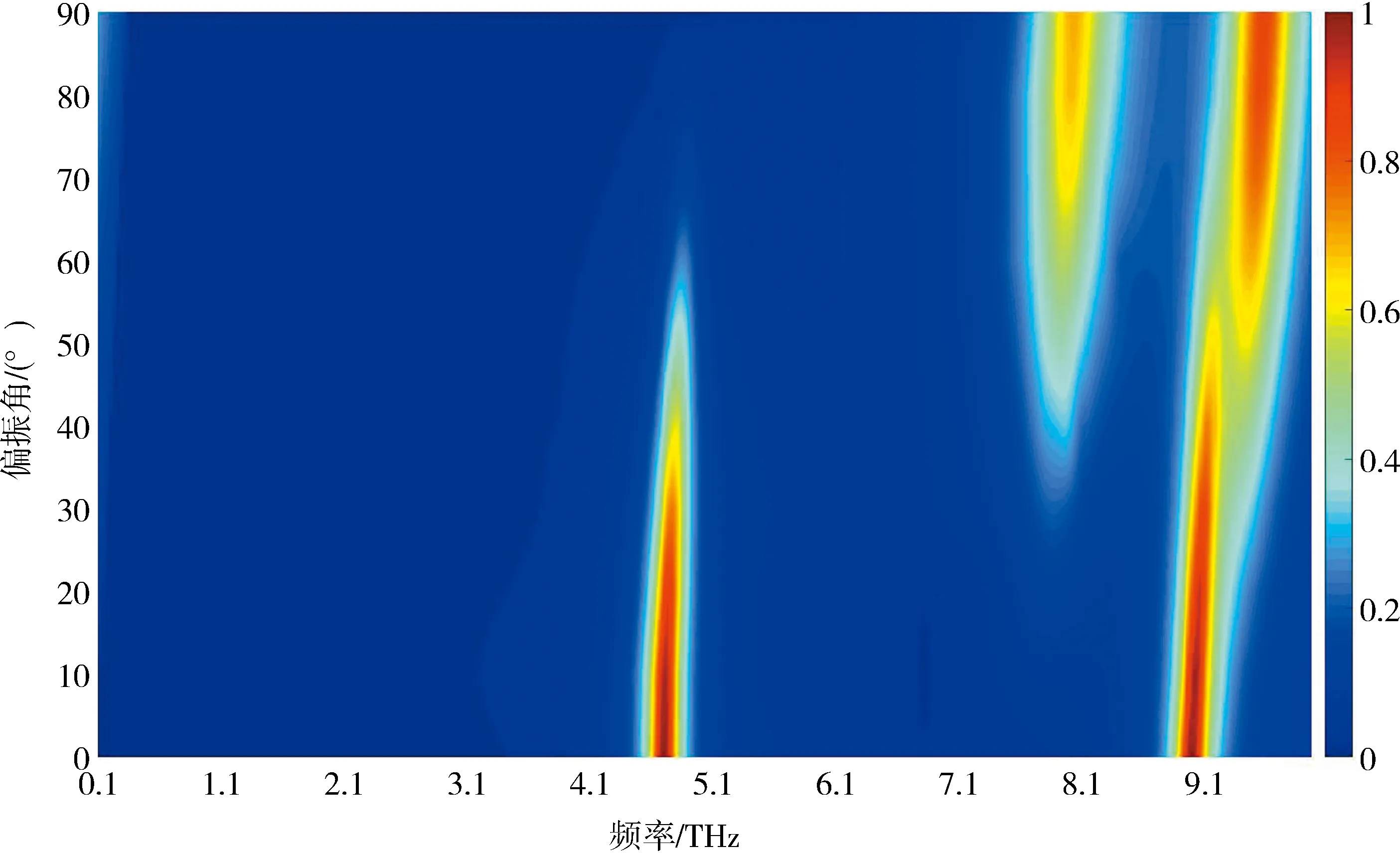
图 11 超材料吸收器(箭头表示方向,颜色表示电场强度)的石墨烯层共振吸收谱

3 结论

综上所述,提出了一种基于圆盘石墨烯的“葫芦形”超材料吸收器,该吸收器结构简单,具有强的可调谐性,可实现THz范围内的单频、双频和多频吸收.仿真计算结果显示,当吸收器表面2个不同半径的石墨烯圆盘具有不同的圆心距可以产生一个或多个吸收峰,而且当圆心距为适当值时,可产生双频的完美吸收.基于产生完美双频吸收的2个石墨烯圆盘葫芦形构型,进一步研究了具有该构型的吸收器吸收曲线随石墨烯费米能和弛豫时间的变化,结果表明该构型的吸收器的吸收性能可以通过外加偏置电压和化学掺杂进行有效的调节.在葫芦形吸收器吸收曲线随弛豫时间的改变过程中,吸收率的调制深度在低频和高频可分别达到20.46%和22.97%.此外,葫芦形构型的吸收器的吸收曲线还可通过旋转入射电磁波的偏振角度来实现双频到多频的可调,调制深度可高达99.95%(低频)和95.22%(高频).仿真结果还显示该吸收器在电磁波大角度的入射下也能保持高的吸收率.跟之前的吸收器相比,该吸收器结构更简单,且可调谐性强,因而在滤波、THz信号检测和传感器等方面具有潜在的应用价值.