当量和爆高(埋深)反演的声震分析方法

张亮永,张德志,肖卫国,梁旭斌,王同东,郭权势,李 翱

(强脉冲辐射环境模拟与效应全国重点实验室;西北核技术研究所：西安710024)

在国防和民用领域中,近地面爆源参数反演是非常重要的研究内容,快速预测爆炸当量和爆高(埋深)(height of burnst, HOB)等源参数,对爆炸事故和恐怖袭击预警[1-4]、地震和火山喷发事件预报[5-7]、核查监测[8-10]及武器性能评估[11-12]等方面具有重要意义。采用声学数据(近区为冲击波)[13-21]或地震波数据(近区为地运动)[2-3, 22-24]预测爆源参数是常见的两种近地面爆源参数反演方法,但采用这两种方法反演的爆炸当量和爆高(埋深)分布在特定范围内存在多个极值点(称为折中关系[22-27]),给源参数估计造成了极大的不确定性。为提高源参数预测的精度,研究人员提出了声震分析方法[22-27],该方法基于数据融合算法综合地震波(地运动)数据和声学(空气超压)数据反演爆源参数,通过同时利用声震波动信息对源参数进行多重约束,减小折中关系的影响。声震分析方法分为声学模型、地震波模型和数据融合算法3个部分,本文将对这3部分目前的进展展开论述。

1 声学模型

由于近地面爆炸能量会耦合到空气中产生明显的声扰动,一般通过远场声学数据,利用超压峰值、正向声冲量及正向脉宽等波形特征量来预测地面爆炸当量[22-27],研究人员相继提出适合快速计算,以超压、声冲量和持续时间为特征量的半经验声学模型及描述波形细节的全波形声学反演方法。半经验声学模型包括ANSI模型[28, 29]、KG85标准模型[30]、BOOM模型[15, 31]和IPM声学模型[19]等自由场声学模型及地面爆炸声学模型[2]和近地面爆炸声学模型[22-26]。半经验自由场声学模型未考虑爆炸能量耦合到地下的影响,对地面爆炸事件通常假设两倍等效爆炸当量进行爆源参数估计[20, 28-30, 32];而对于近地面爆炸事件,Zhang等[33-34]通过考虑地面反射、耦合作用及大气环境因素,建立了基于自由场声学模型的近地面声学模型(简称为自由场近地面声学模型),进行了爆炸当量和爆高估计。表1为不同的自由场声学模型。地面爆炸声学模型[2]是基于地面爆炸声学数据建立的模型,考虑了地面爆炸能量耦合情况,用于地面爆炸事件的当量估计,但不适用于偏离地面位置的爆炸事件当量估计。而近地面爆炸声学模型考虑了近地面声震能量耦合特性,可用于近地面爆炸事件的当量和爆高(埋深)估计,但不适用比爆高为-2.4 ～-0.6 m·kg-1/3的浅埋情况。上述两种模型需根据不同场地介质提前确定多个待定系数,适用的场地介质有限。Zhang等[25]在近地面爆炸声来源机制[35-36]的基础上,通过考虑气体喷出地表和地冲击耦合影响对近地面声学模型进行改进,拓宽了比例爆高适用范围,同时确定了花岗岩夹杂变质岩场地的模型待定系数。图1为近地面爆炸声来源机制[35-36]和改进前后近地面声学模型[25]。

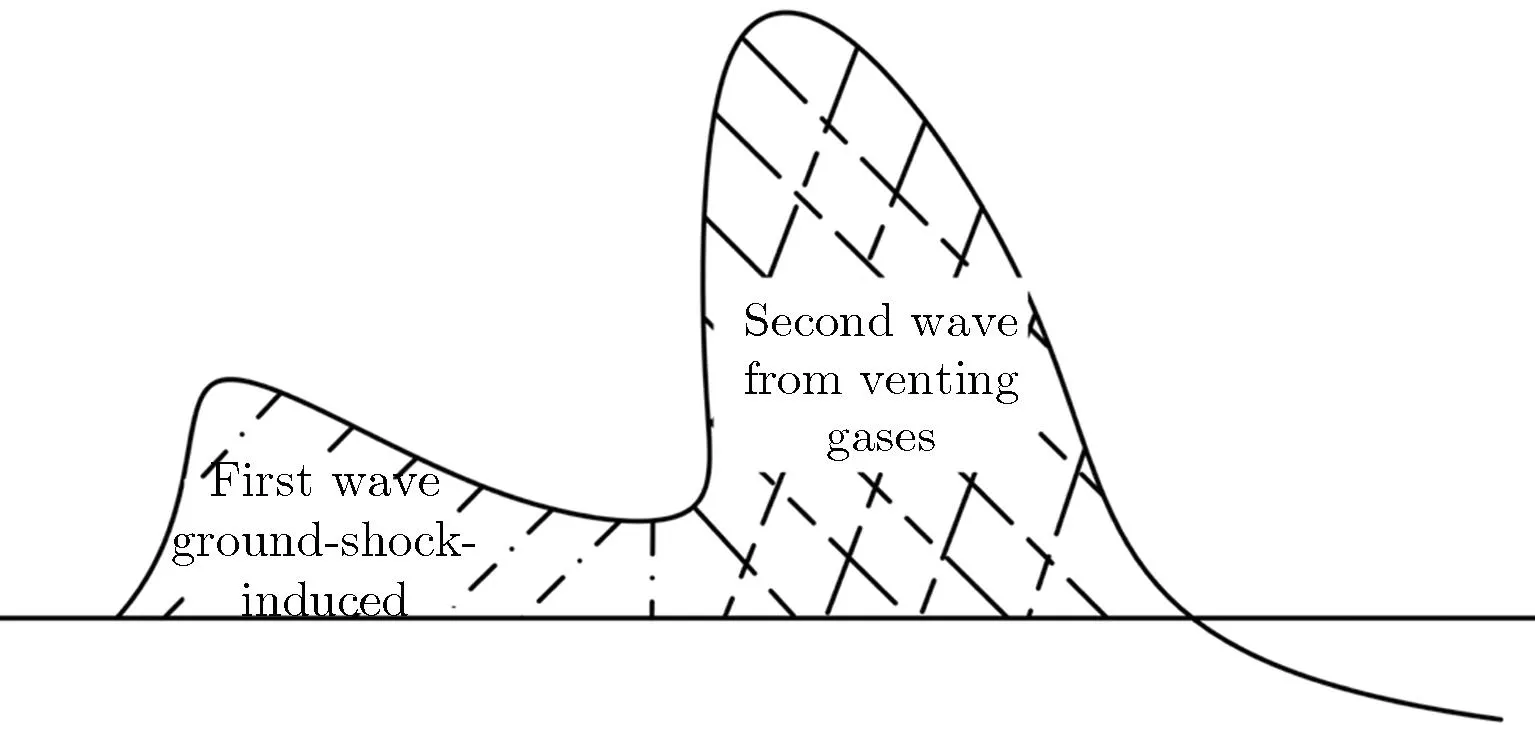
(a)Mechanism of near-surface explosion producing sound [35-36]

(b)Unimproved and improved near-surface acoustic models[25]

表1 自由场声学模型

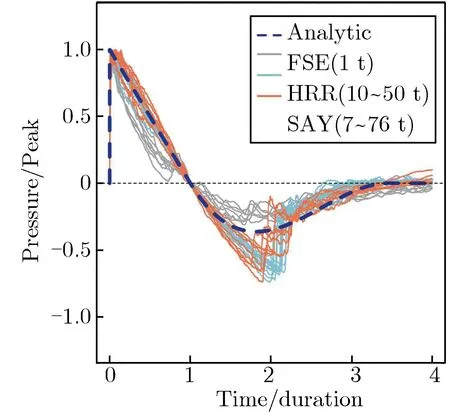
全波形声学反演方法包括超压波形模板匹配法[16]、经验声源模型法[20]和折合声冲量法[14, 17, 24]等。超压波形模板匹配法[16]以不同比距离下随比时间变化的大量压力波形数据为模板,将未知当量的全压力波形和模板压力波形进行匹配,对应匹配偏差最小的当量为估计当量,但该方法需大量不同当量不同比距离的压力波形组成的样本库,但目前样本数据库还不够充分;经验声源模型法[20]以G17HE为标准源模型,通过大量实测视压力数据并假设标准高斯分布,获取源模型的峰值压力和持续时间平均值和方差(偏差分布),由此计算爆炸当量,但该模型声测点数据需选取20～100 m·kg-1/3的比距离范围,在未知当量时不好提前预设测点距离。图2为超压波形样本库[16]以及G17HE源模型和实测波形[20]。Kim等[14, 17]基于线性声学理论反演爆源等效源时间函数,以KG85模型折合声冲量作为参考函数,提出一种地面爆炸当量反演思路(本文称为折合声冲量法),并将其应用于刚性地面爆炸当量反演,具有较高的当量预测精度,但该方法只适用刚性地面爆炸当量估计,没有考虑波传播过程中地表结构的影响。图3为等效源时间函数及预测和实测波形。张亮永等[37]对该方法进行了发展,通过考虑波传播过程中地表结构的吸收衰减影响及近地面爆炸声震能量分配过程,建立了多孔弹性场地近地面折合声冲量模型,解决了多孔弹性场地的当量估计问题,给出当量相对偏差为7%,爆高相对偏差不超过19%。图4为多孔弹性场地声传播示意图和爆源参数反演结果。

(a)Pressure wave template[16] producing sound [35-36]

(b)Source model of G17HE with measured waveforms [20] acoustic models[25]

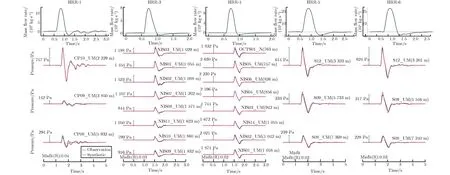
图3 等效源时间函数(顶端黑色曲线)及预测(红色曲线)和实测(黑色曲线)波形[14]

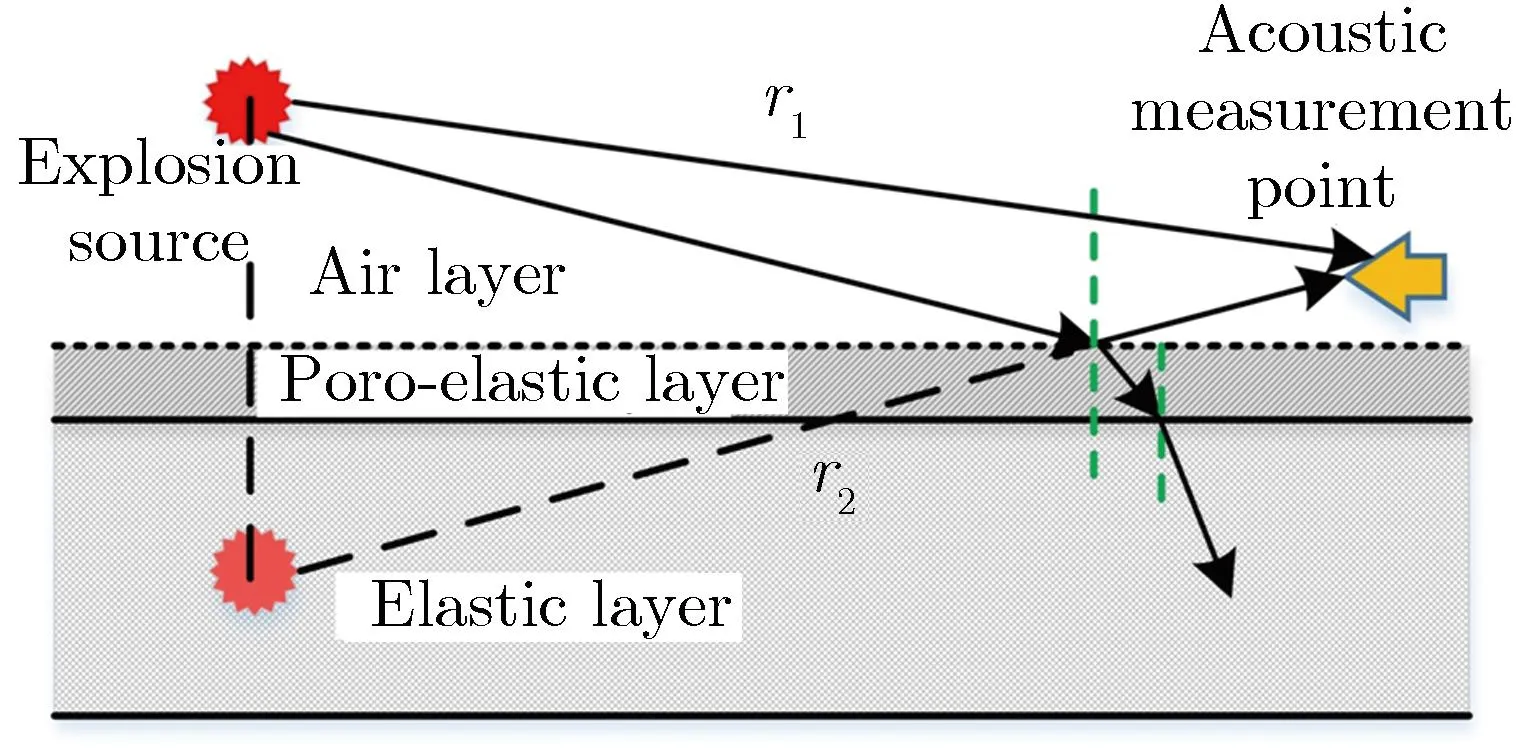
(a)Sound propagation diagram in three-layer medium model

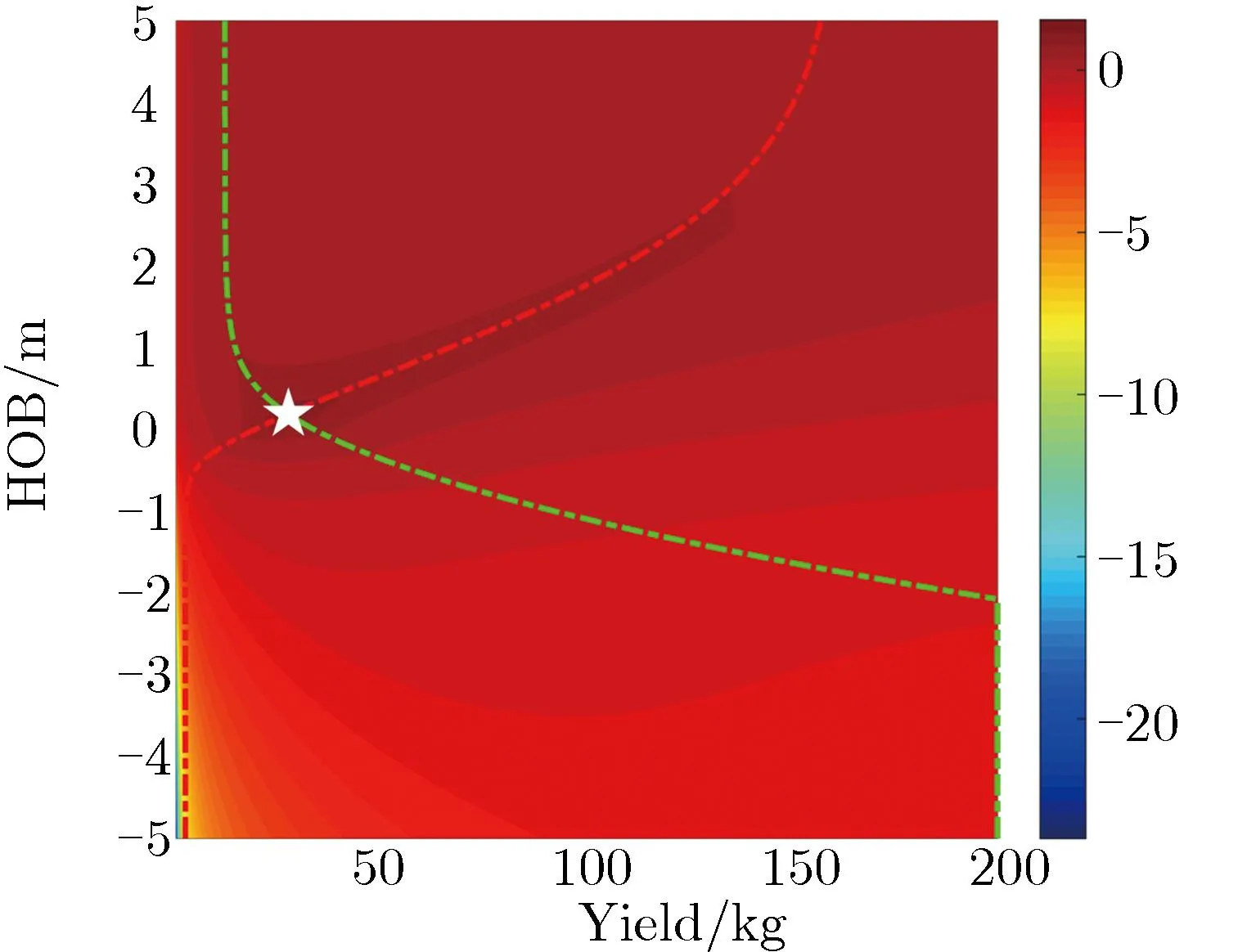
(b)Yield and height of burst predicted by seismoacoustic analysis

2 地震波模型

近地面爆炸耦合的地震波(近距离称为地冲击或地运动)来源于爆炸直接耦合方式和空气超压(声波)耦合方式,对近距离前者称为直接地冲击,后者称为感生地冲击[12, 38-39],而对远距离,Albert等[40]将前者耦合的地震波称为前驱地震波,后者耦合的地震波称为声耦合地震波。图5为近地面爆炸耦合的地震波来源方式示意图。

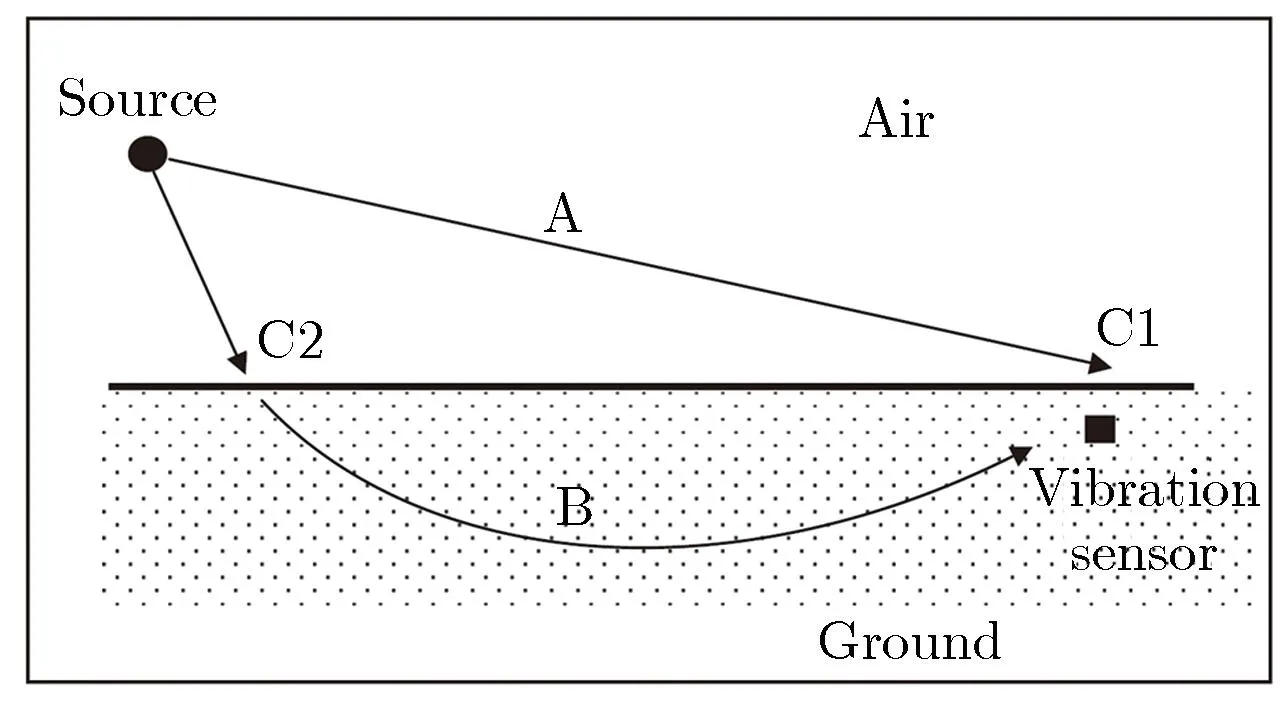
图5 近地面爆炸耦合的地震波来源方式示意图[40]

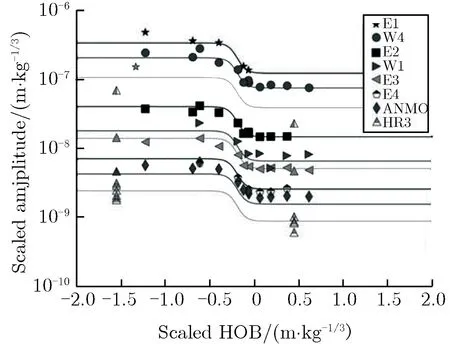
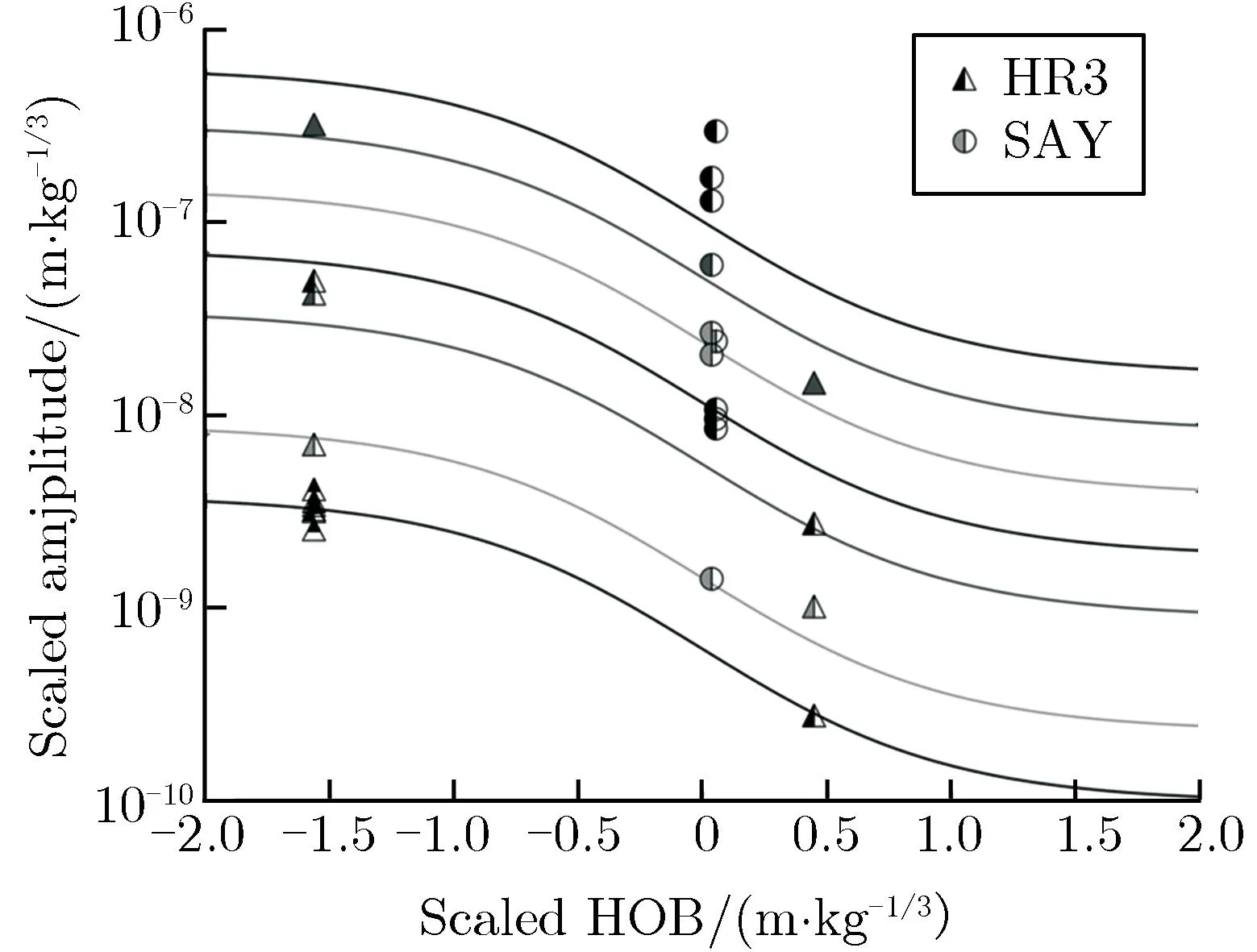
目前,近地面地震波模型以前驱地震波模型为主,随着DM/DB[2],HRI-III[16, 23, 41],SAY[22, 42],FSE和SPE[24]等系列化爆试验的开展,相继建立了冲积土、沉积岩和花岗岩等场地介质的近地面前驱地震波爆炸当量估计模型[23-24, 26, 42]。其中,Templeton 等[42]基于HRI-III 和SAY 化爆试验地震波数据对地震波模型进行了深入讨论,对比和分析了冲积土和沉积岩两种地质成分下的近地面爆炸地震波模型,建立了地震波数据分析和模型建立的基本方法,对近地面化爆地震波建模具有指导意义。图6为不同场地介质的近地面地震波模型和实测数据。但上述化爆试验场地介质类型主要是冲积土、沉积岩和花岗岩等,受试验地质成分的限制,地震波模型局限在以上几种地质成分,数据还不够充分,模型还不够完善[22, 24, 42-43],且未考虑爆源附近地质和其余位置地质不一样的情况。

(a)Alluvium

(b)Sedimentary rock

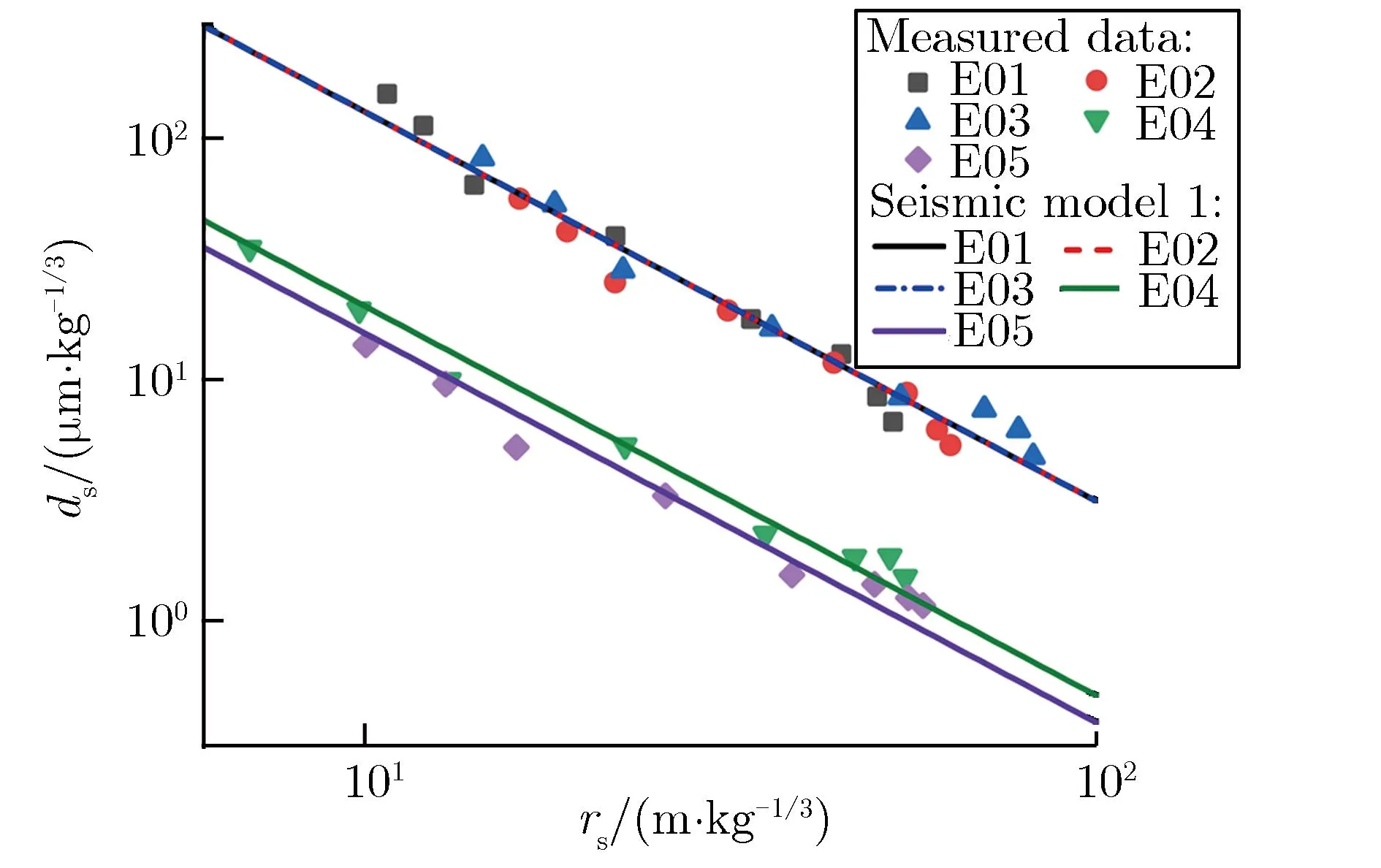
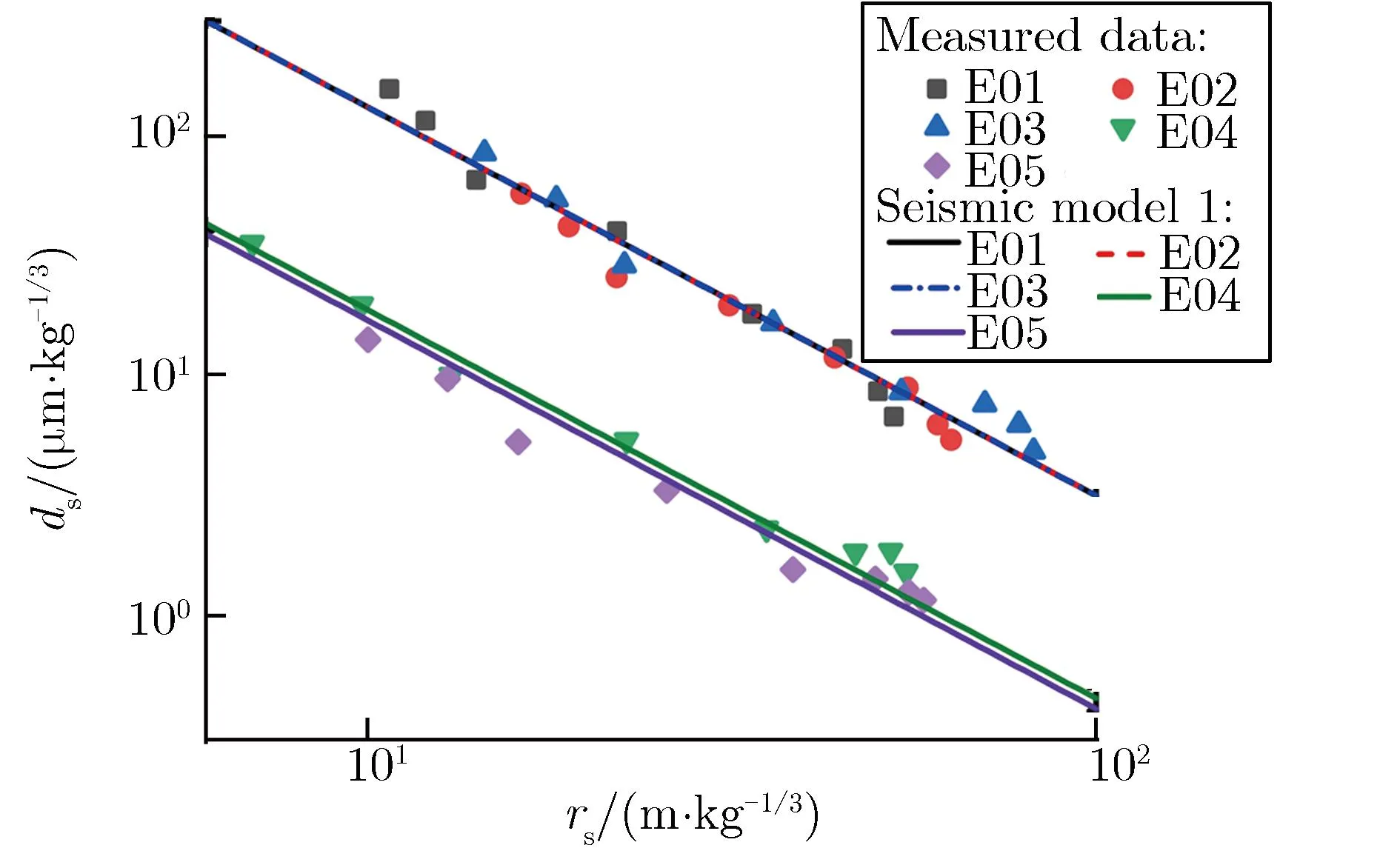
Zhang等[25, 34, 44]基于试验数据探讨了花岗岩夹杂变质岩场地和土石混合场地的近地面地震波实测数据和模型,分别如图7和图8所示。

(a)Seismic data

(b)Seismic model

(a)Model one

(b)Model two

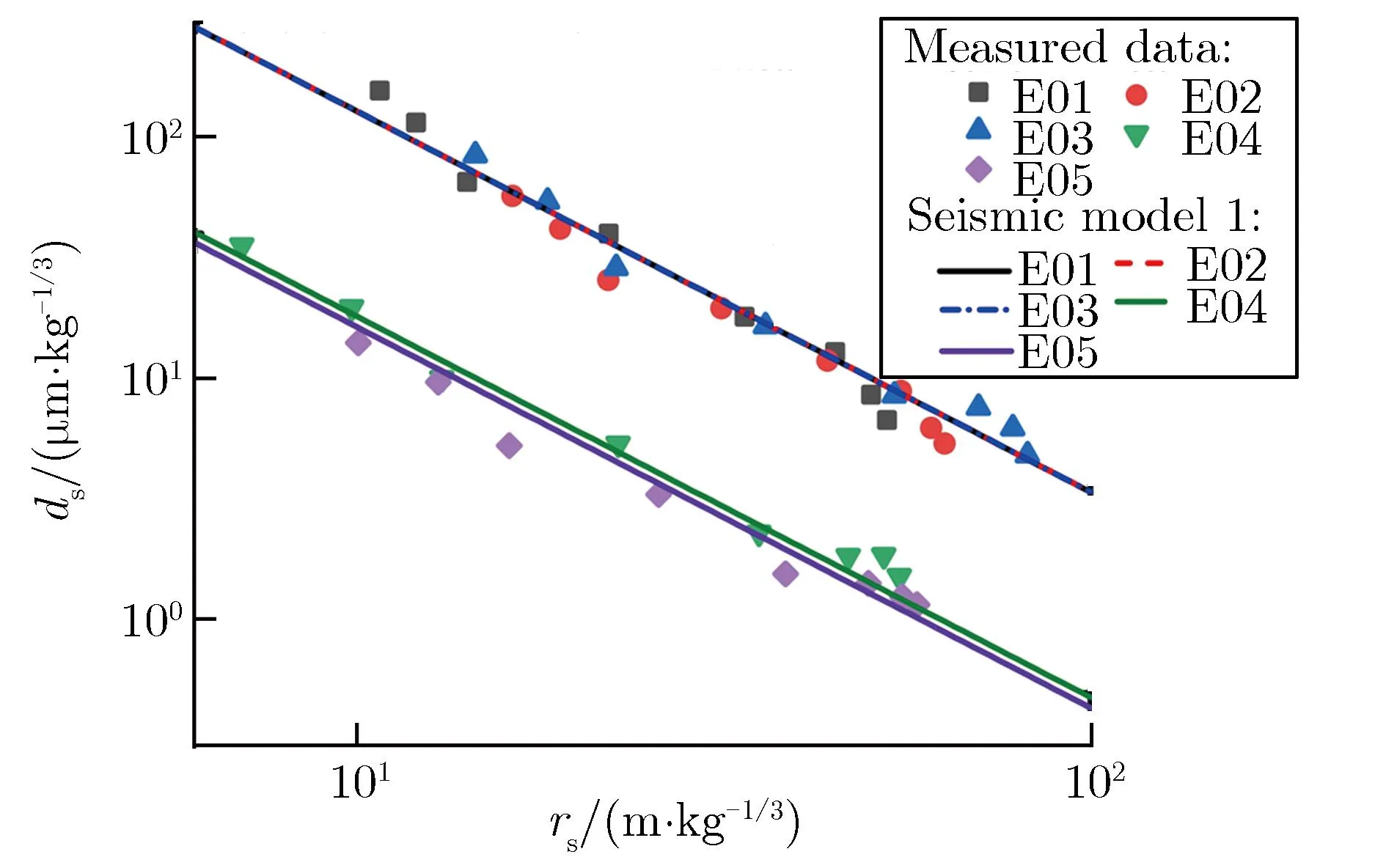
(c)Model three

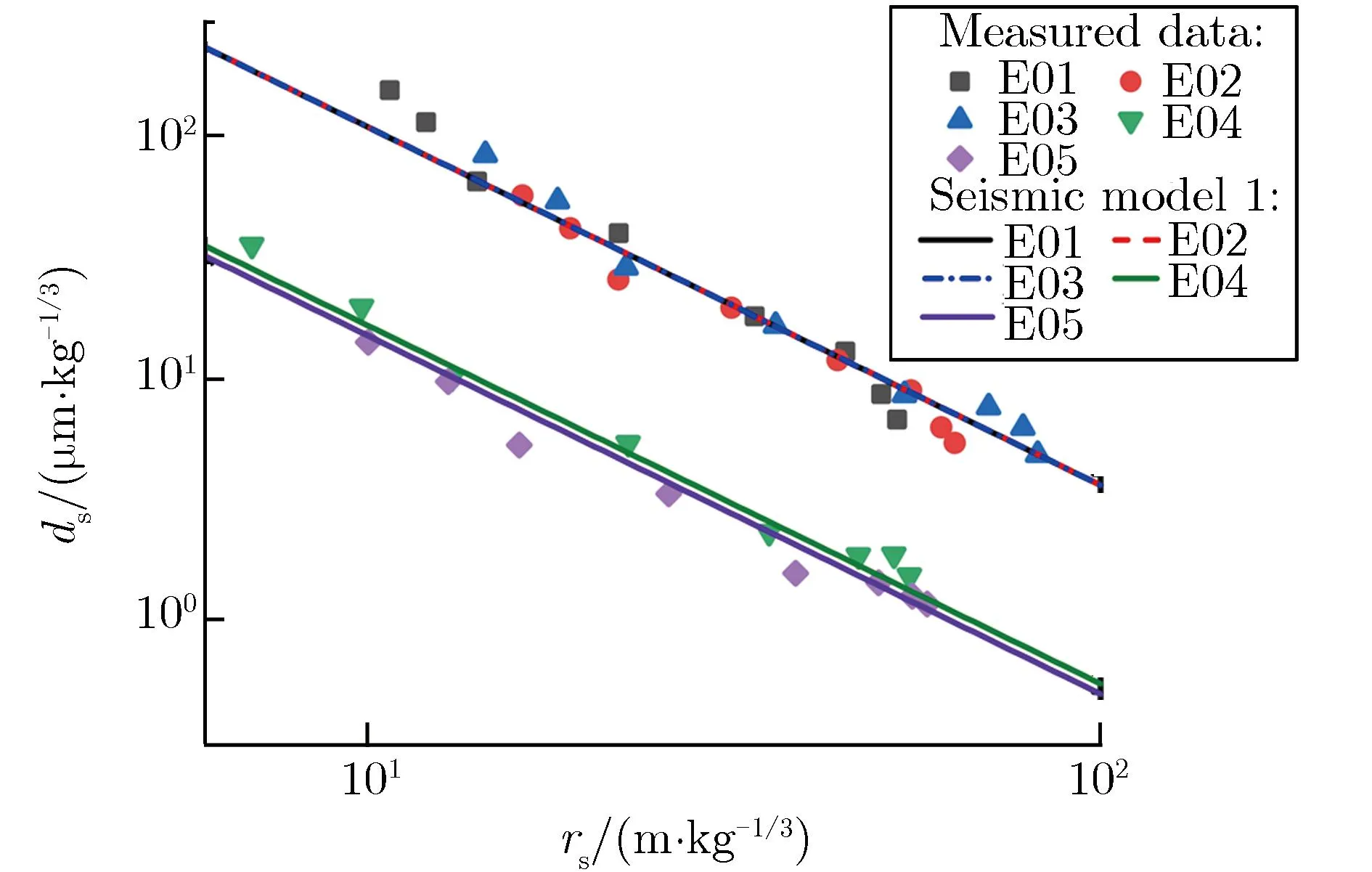
(d)Model four

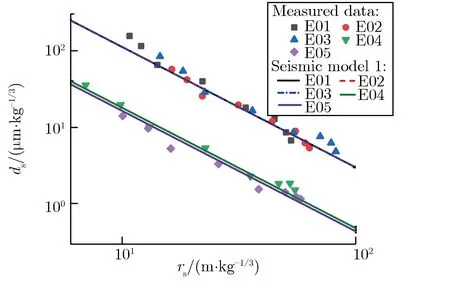
(e)Model five

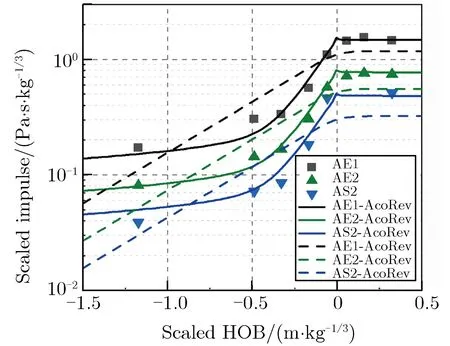
为解决爆源附近地质和其余位置地质不一样的混合场地地震波模型建模问题,给出了模型的待定系数,并通过引入放大系数。图9为放大系数K不同取值对反演结果的影响。图9中,绿色、红色虚线分别为声耦合地震波模型和地震波位移首峰值模型的折中曲线(最小偏差对应的当量和埋深),白色五角星为交叉和最小偏差位置。表2为土石混合场地不同模型的定义。

(a)K=2

(b)K=4

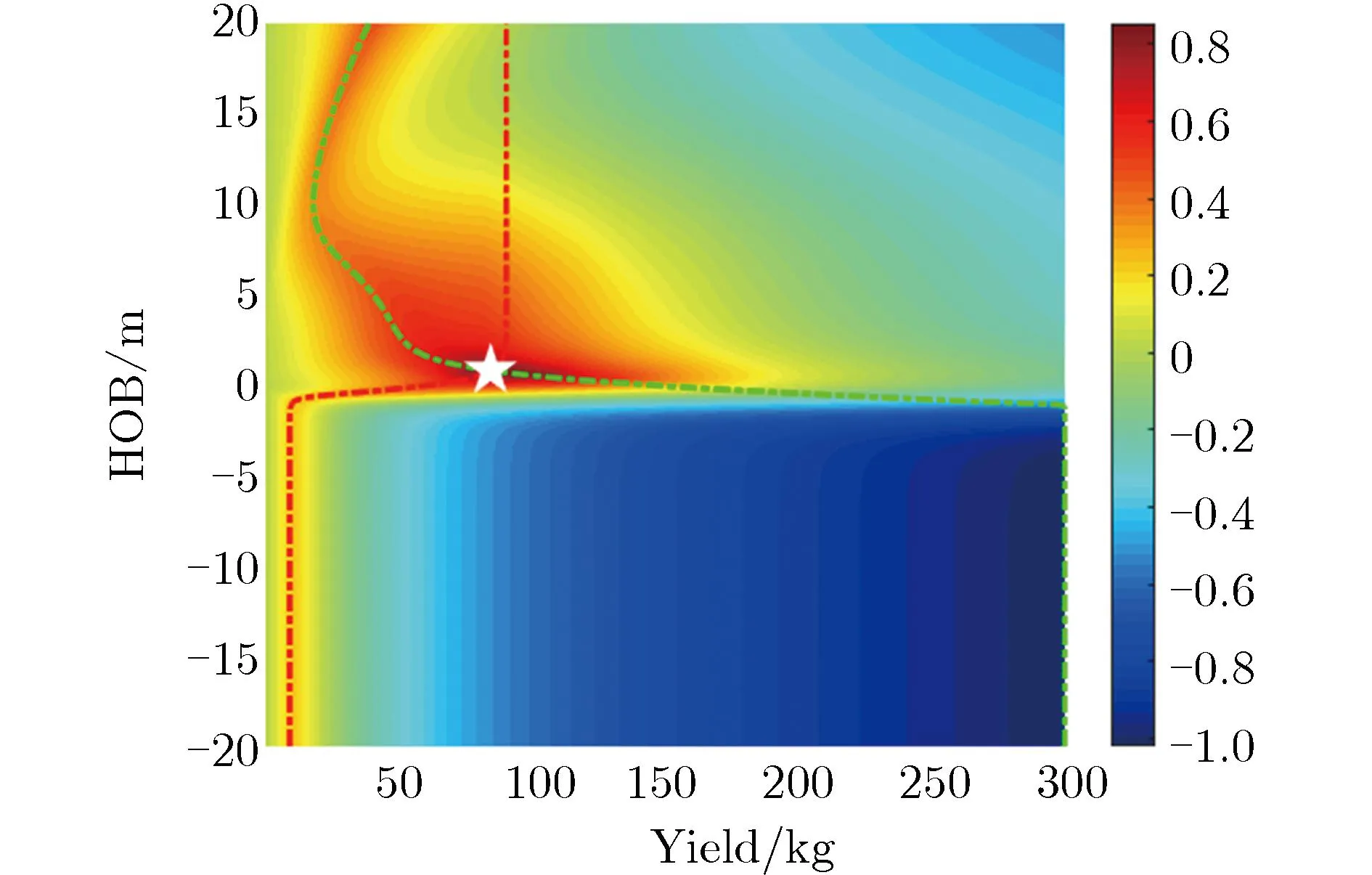
(c)K=6

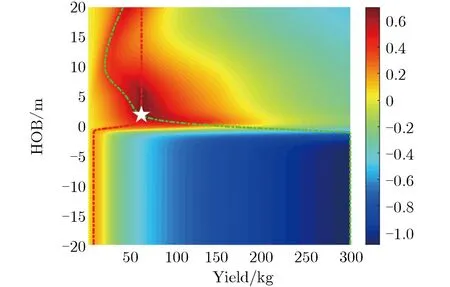
(d)K=10

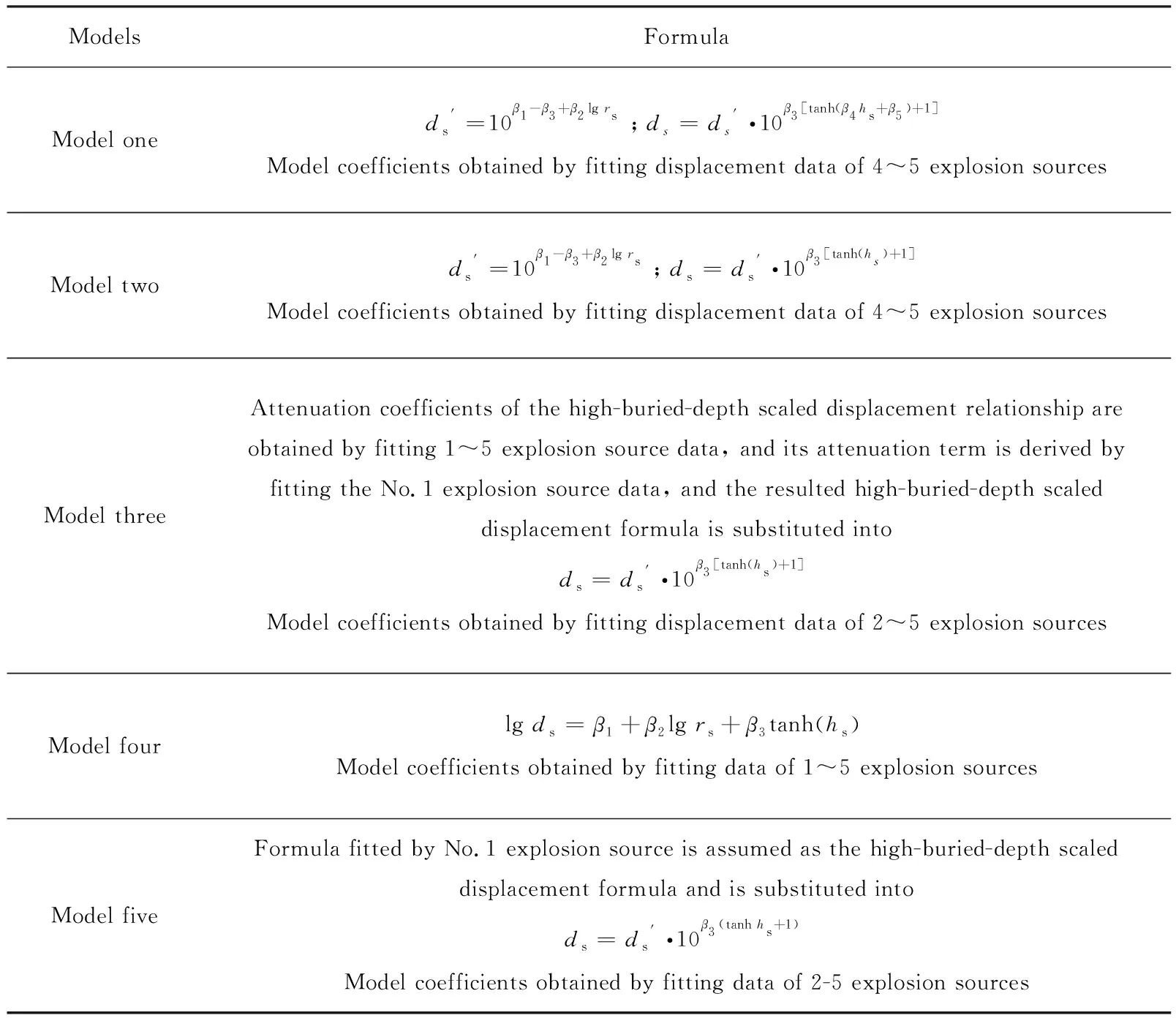
表2 土石混合场地模型的定义[44]

上述近地面前驱地震波模型,基于初至波首峰值建立当量和爆高(埋深)关系,适用中近区爆炸当量估计。对于远区情况,Pasyanos等[10, 24]基于近地面爆炸地震波能量耦合关系,采用地震波尾波包络法,建立近地面远区地震波模型,进一步拓展了近地面地震波模型的适用范围。图10为尾波包络法示意图[46]和典型反演结果[24]。

(a)Schematic diagram of coda-wave method

(b)Typical inversion results

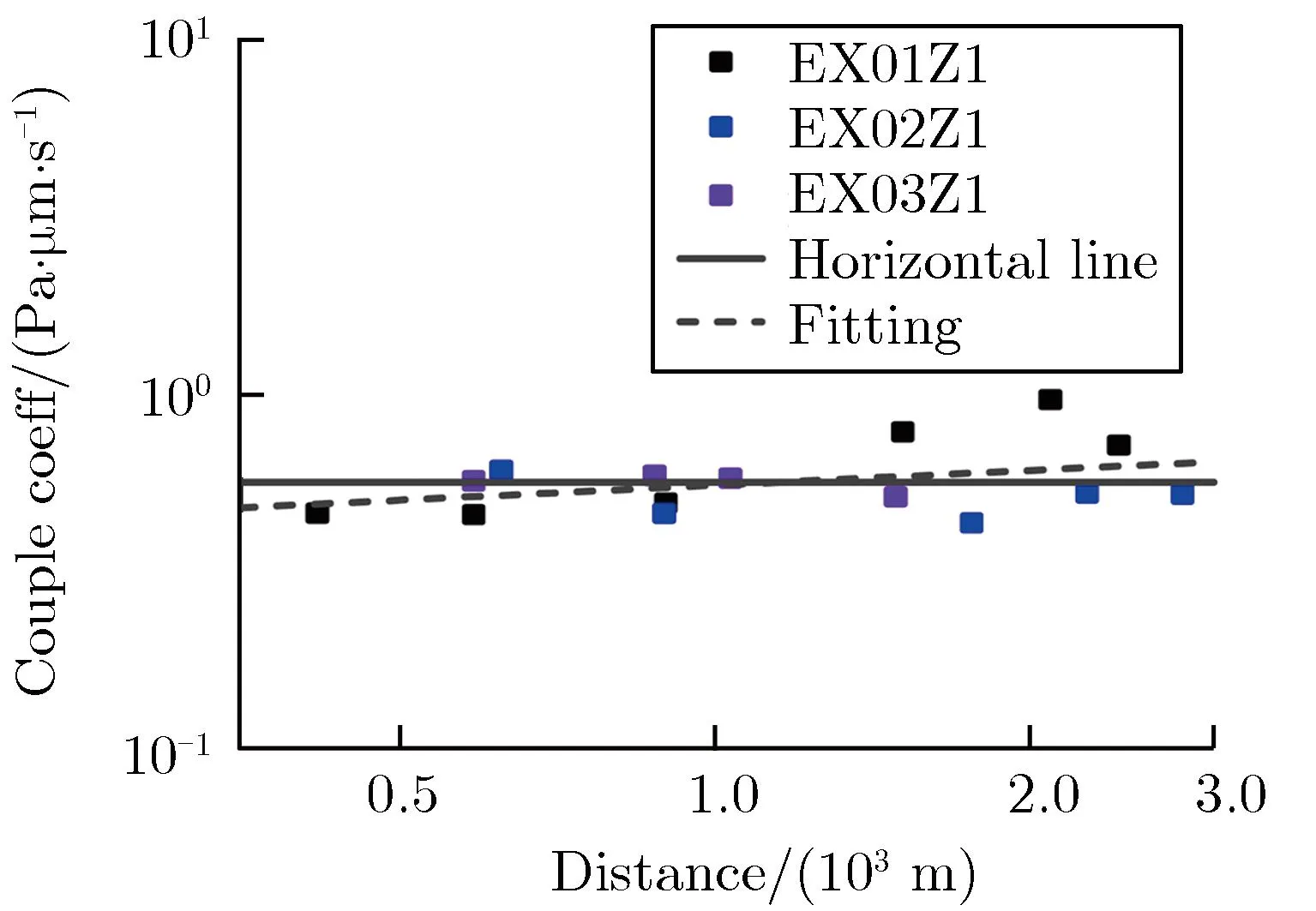
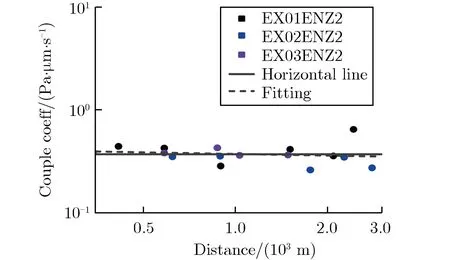
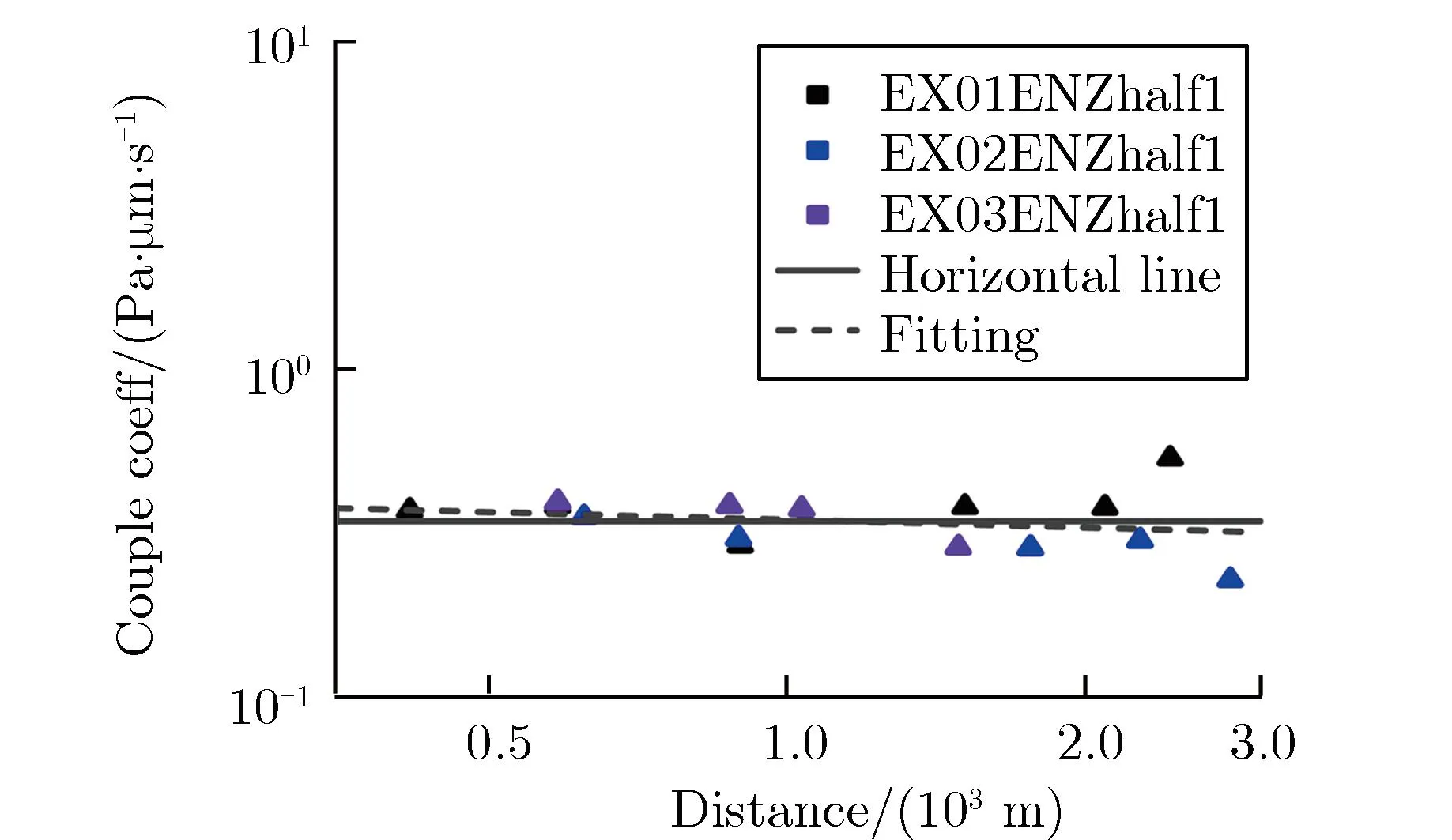
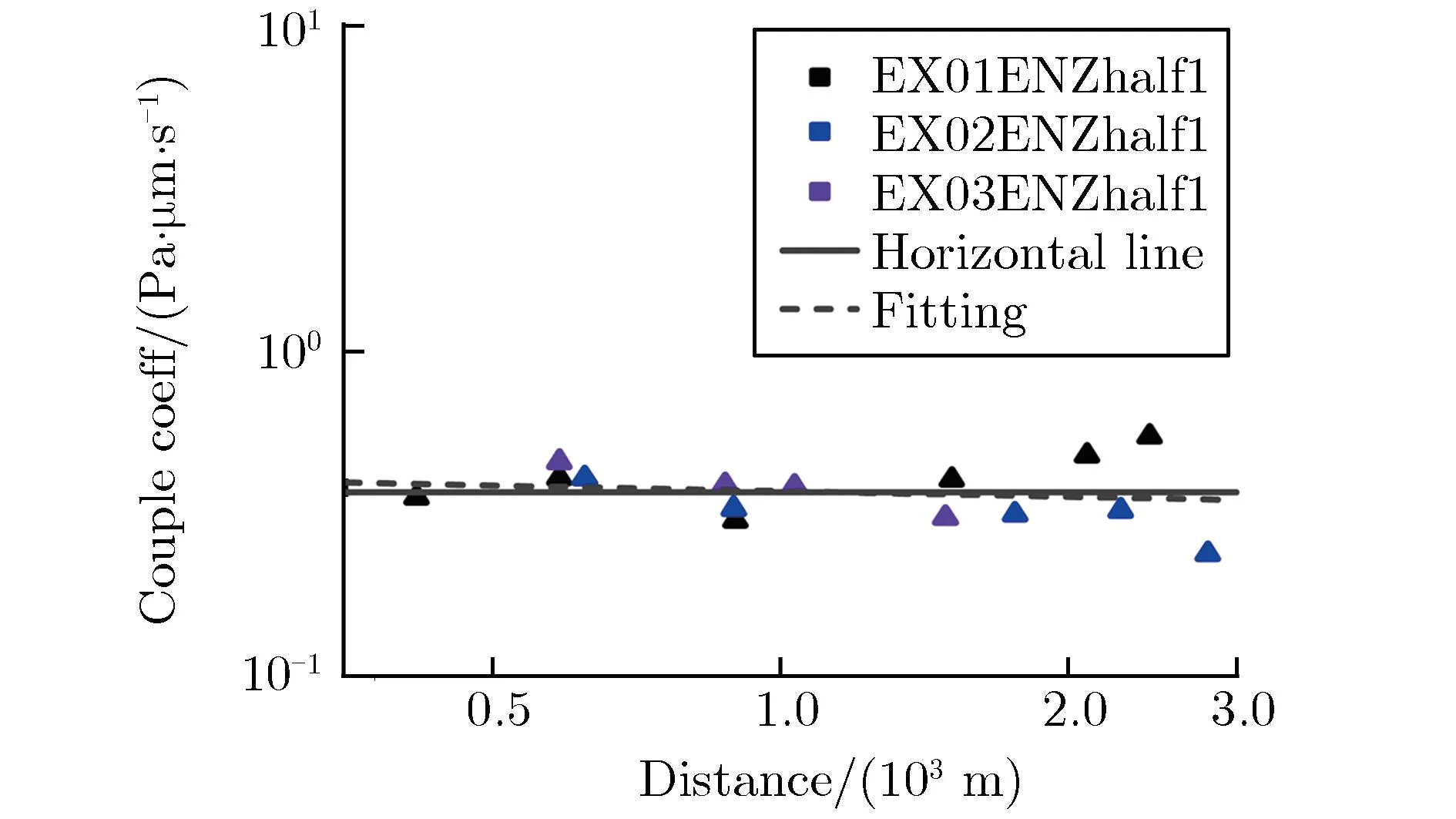
声耦合地震波模型可解决单一地震计的近地面爆源当量估计问题,为爆源参数反演提供除前驱地震波外的新途径,但相关研究较少。Zhang等[46-47]基于声耦合系数建立声耦合地震幅值和声学幅值之间的关系,确定沙土场地的声震耦合系数,并联合近地面声学模型建立声耦合地震波模型。沙场地声耦合地震波典型波形及耦合系数衰减特性分别如图11和图12所示[46]。表3为声耦合地震波特征值的定义[46]。

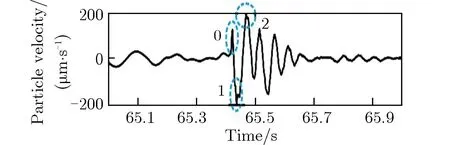
(a)East

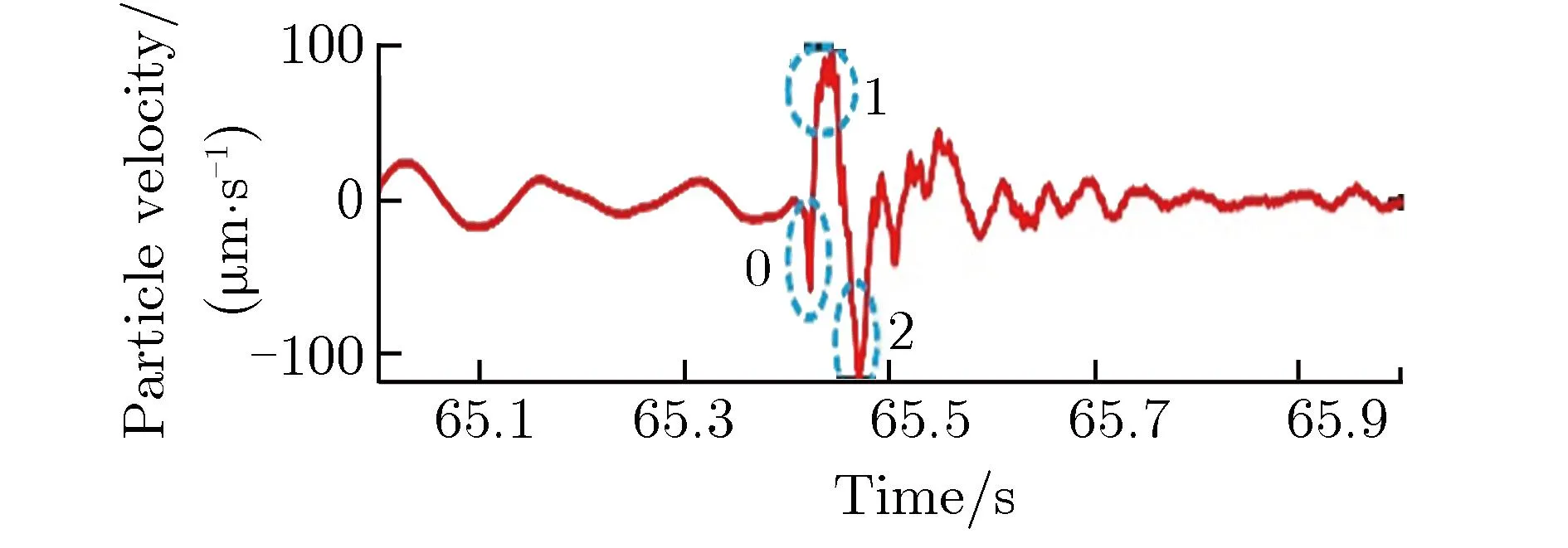
(b)North

(c)Verticle

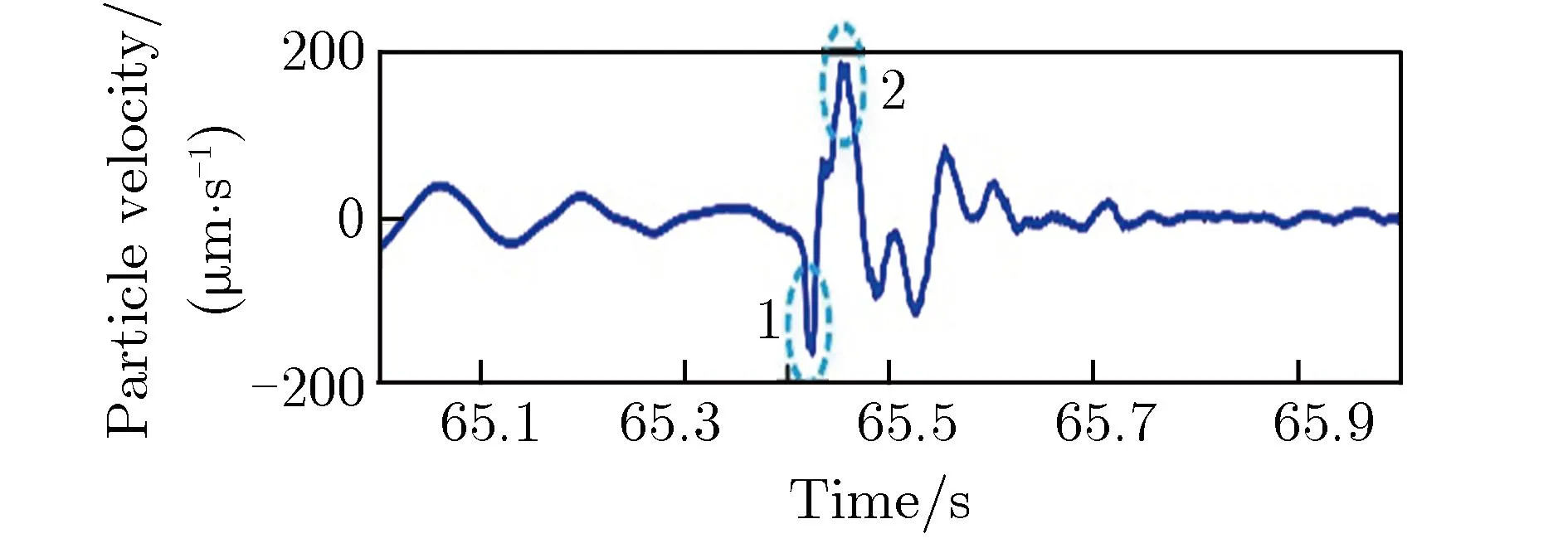
(a)Z1

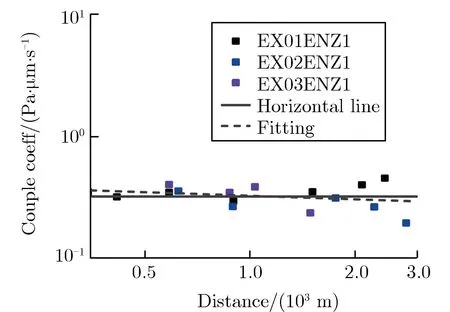
(b)ENZ1 1&2

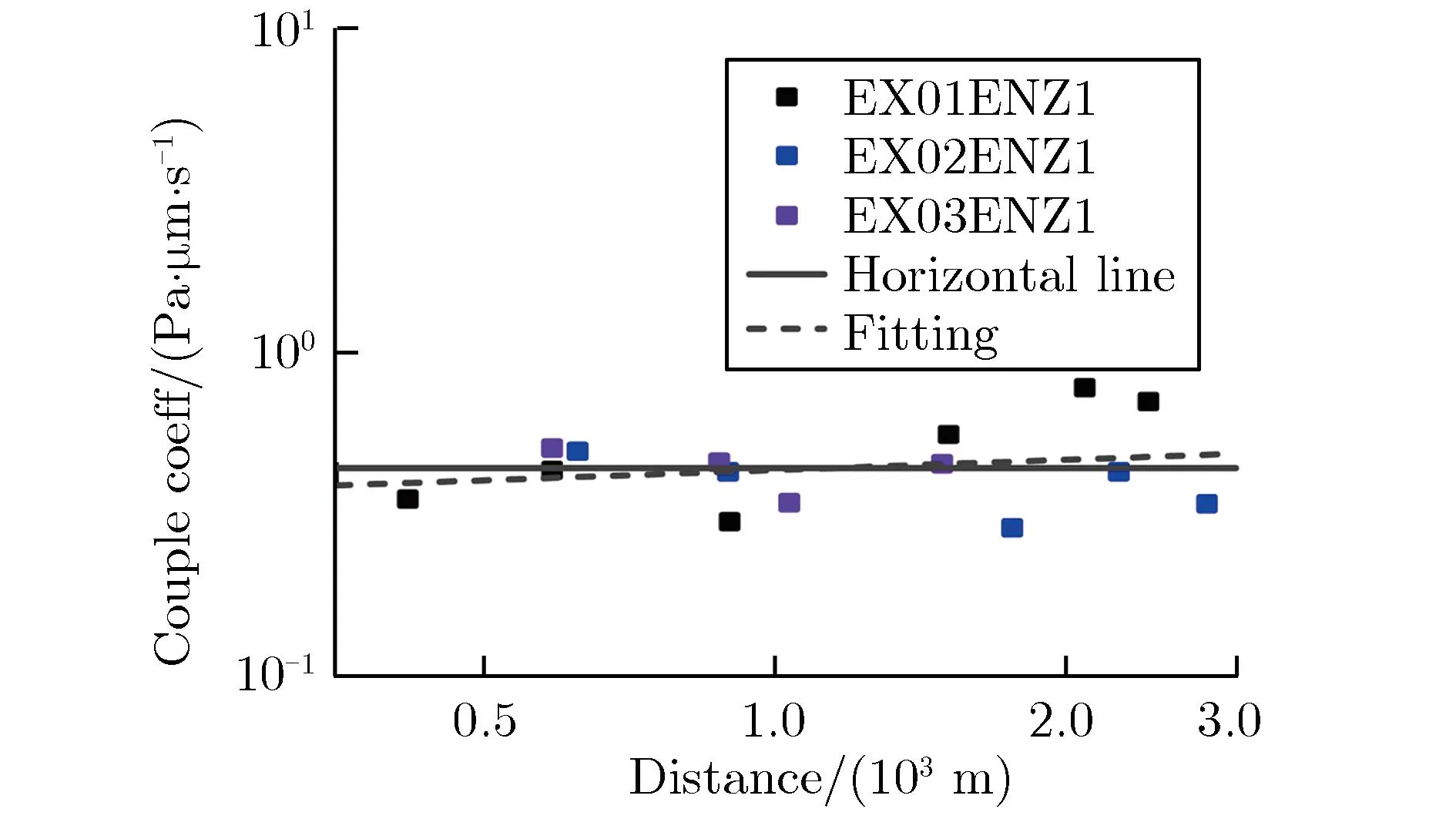
(c)ENZ1 0&1

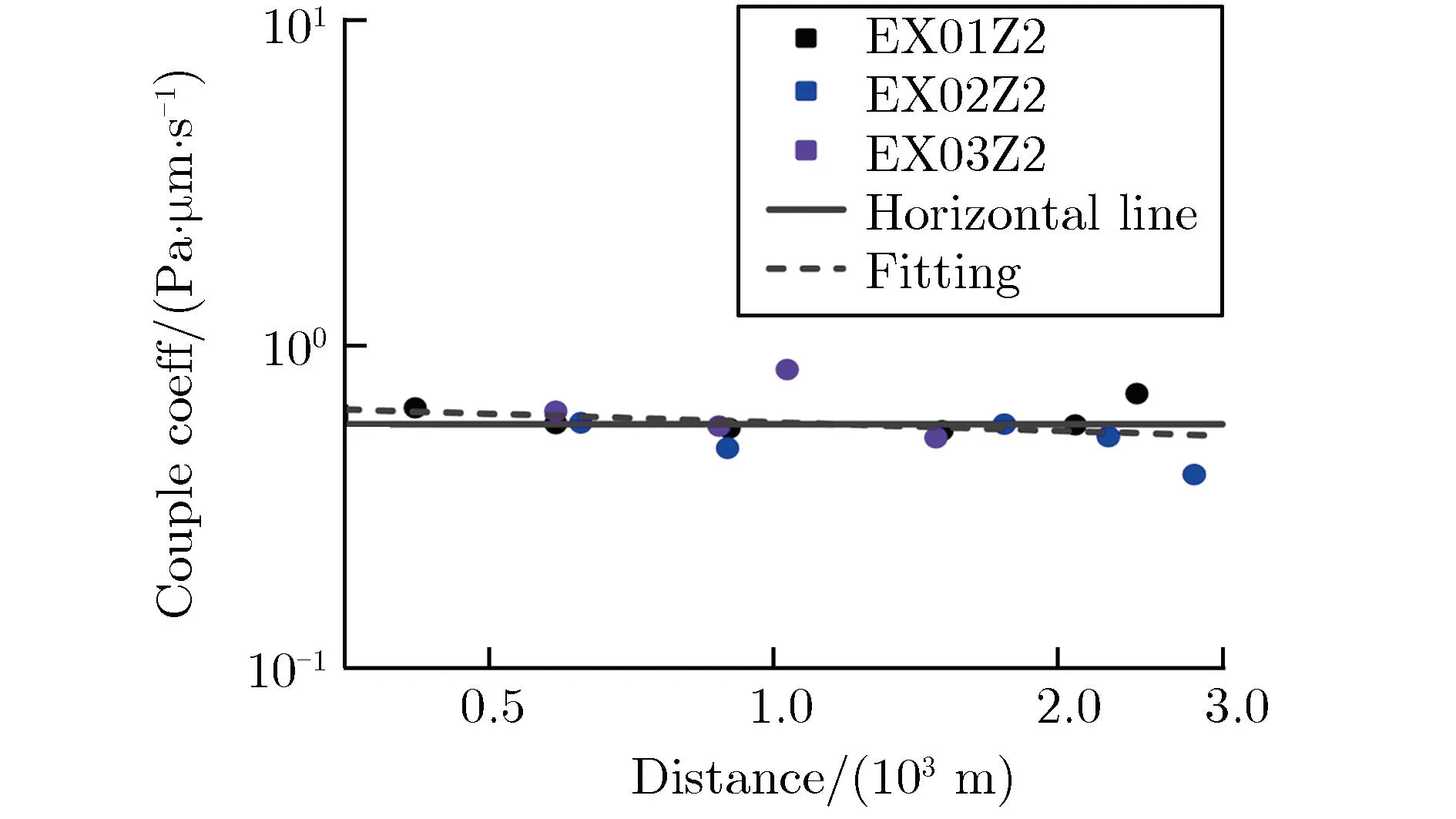
(d)Z2

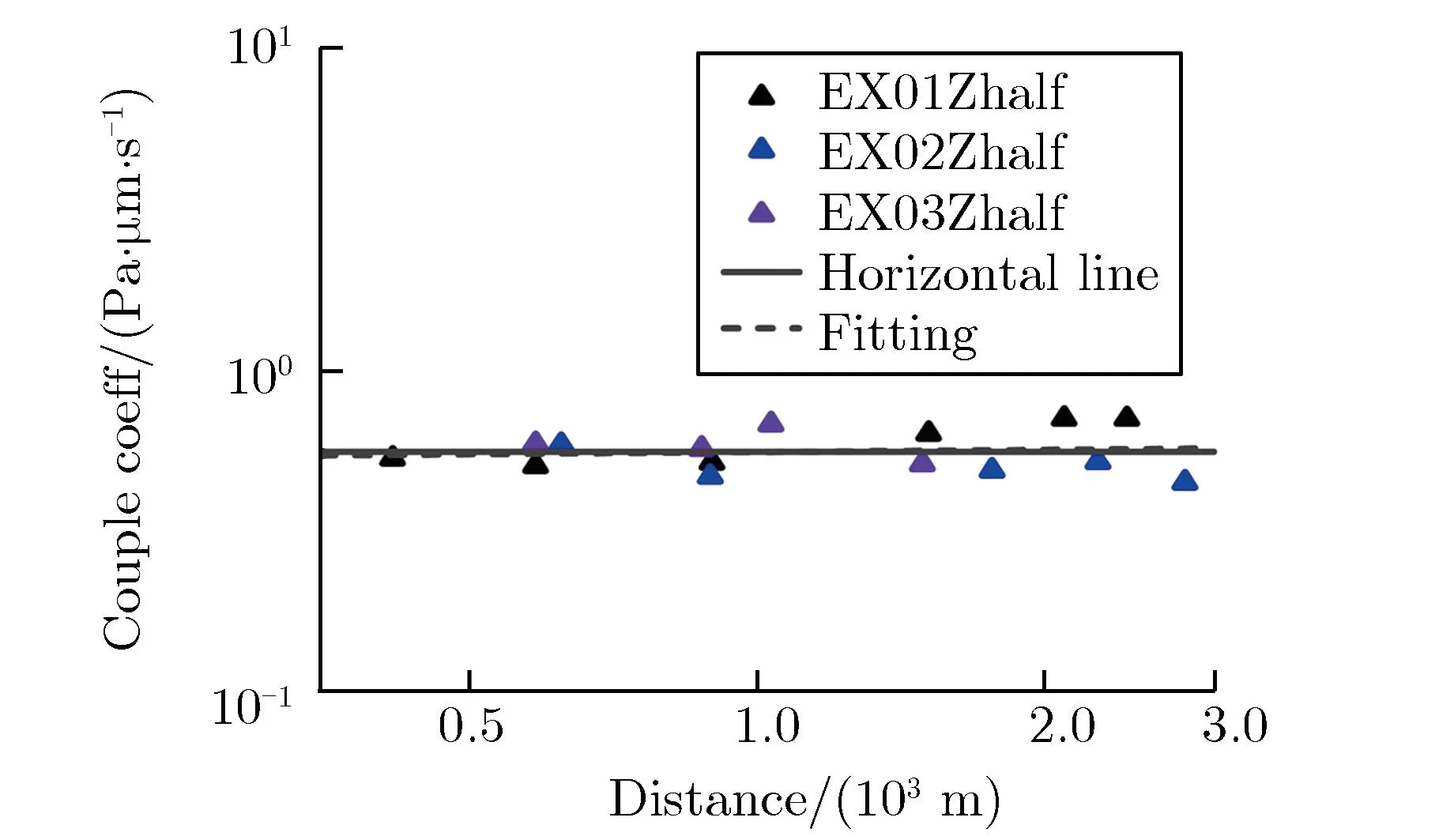
(e)Zhalf

(f)ENZ2 1&2

(g)ENZhalf1 1&2

(h)ENZ2 0&1

(i)ENZhalf1 0&1

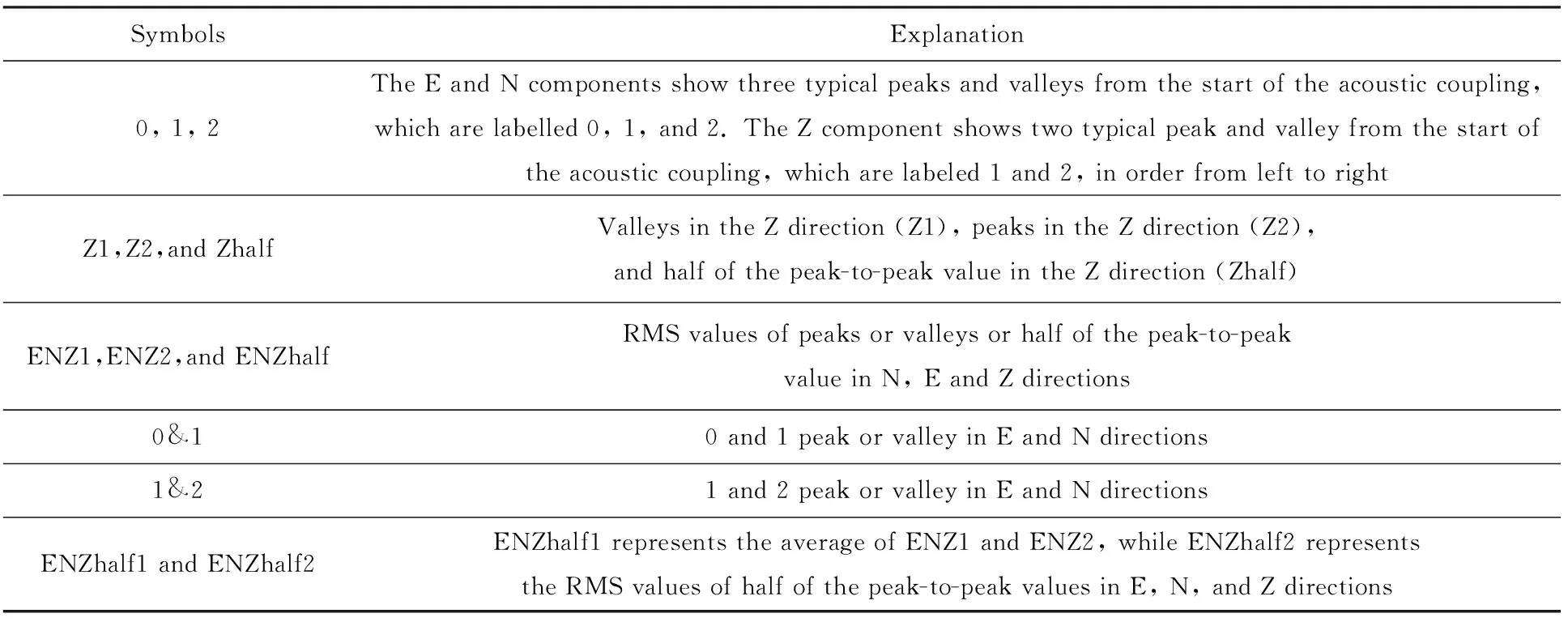
表3 声耦合地震波特征值的定义[46]

3 数据融合算法

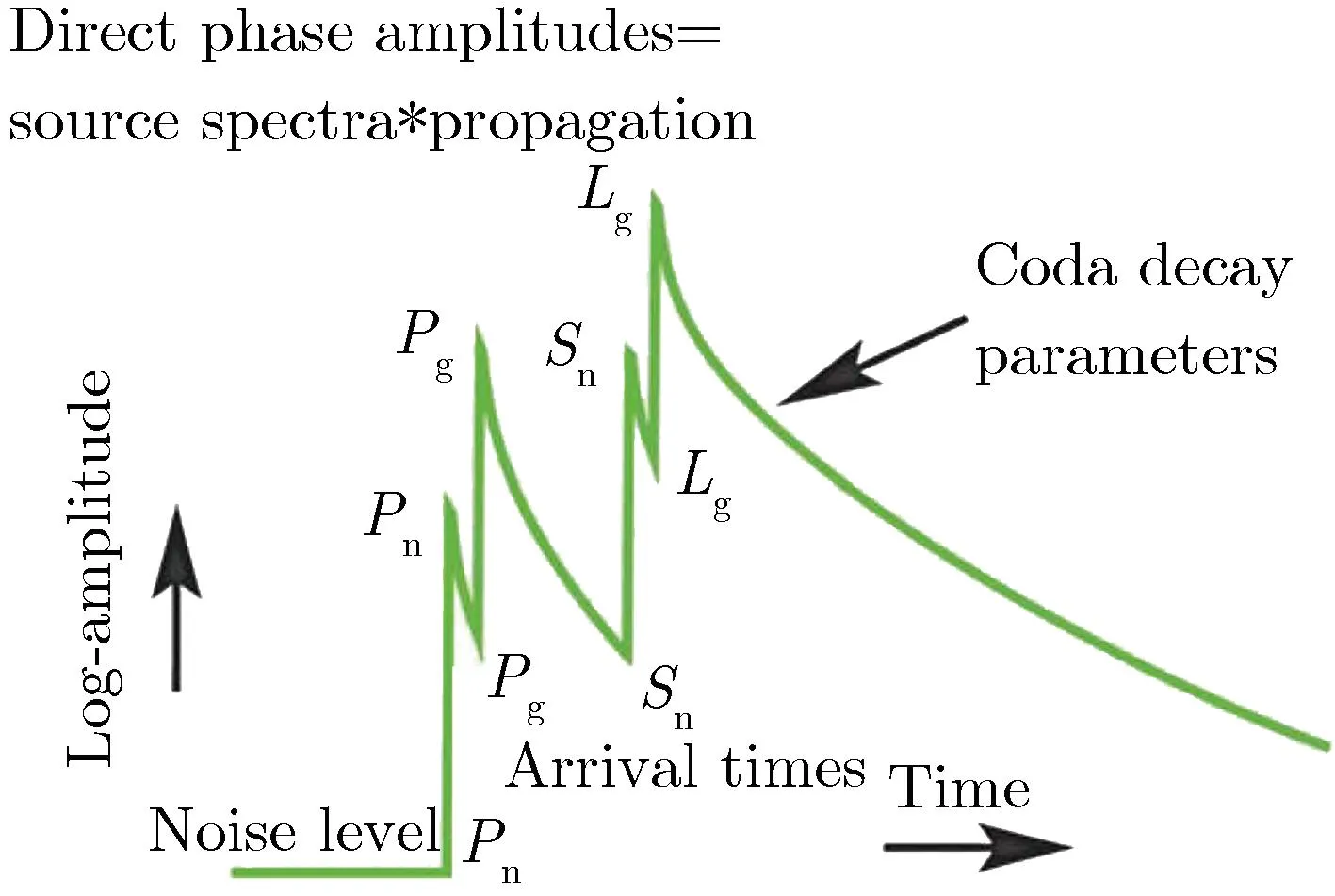
近地面爆炸能量会耦合到大气和地介质中,产生大气扰动(远场为声波)和地运动(远场为地震波)。图13为近地面爆炸产生的典型声震信号[23]。

(a)Seismo-acoustic energy distribution

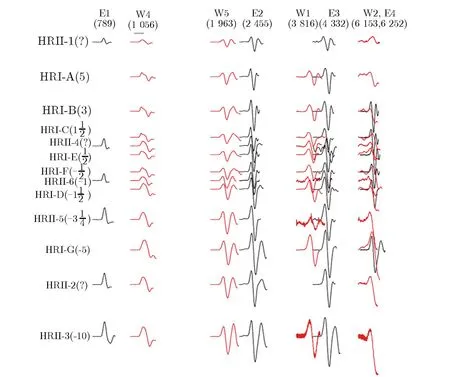
(b)Seismic data of HRI and HRII

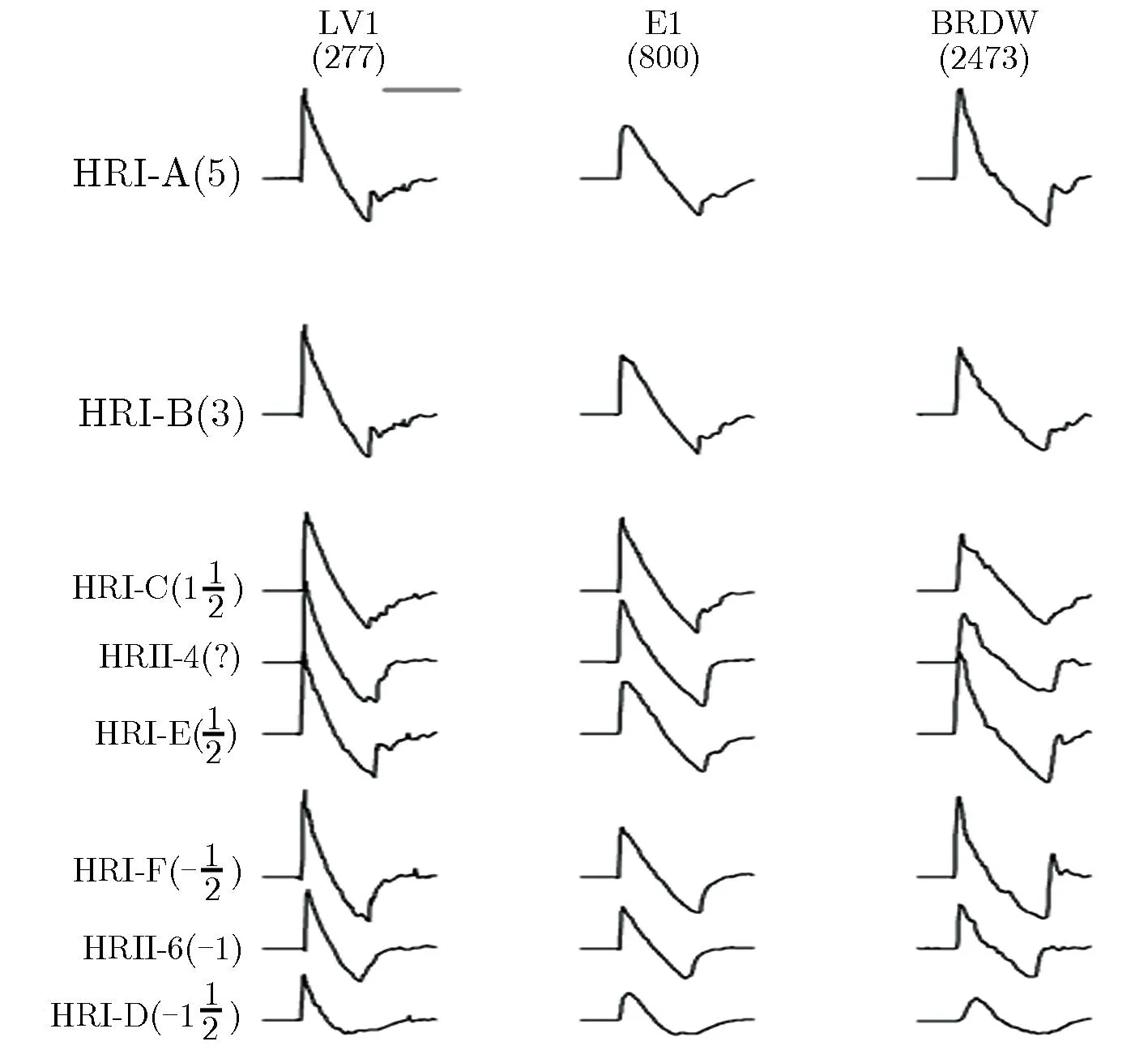
(c)Acoustic data of HRI and HRII

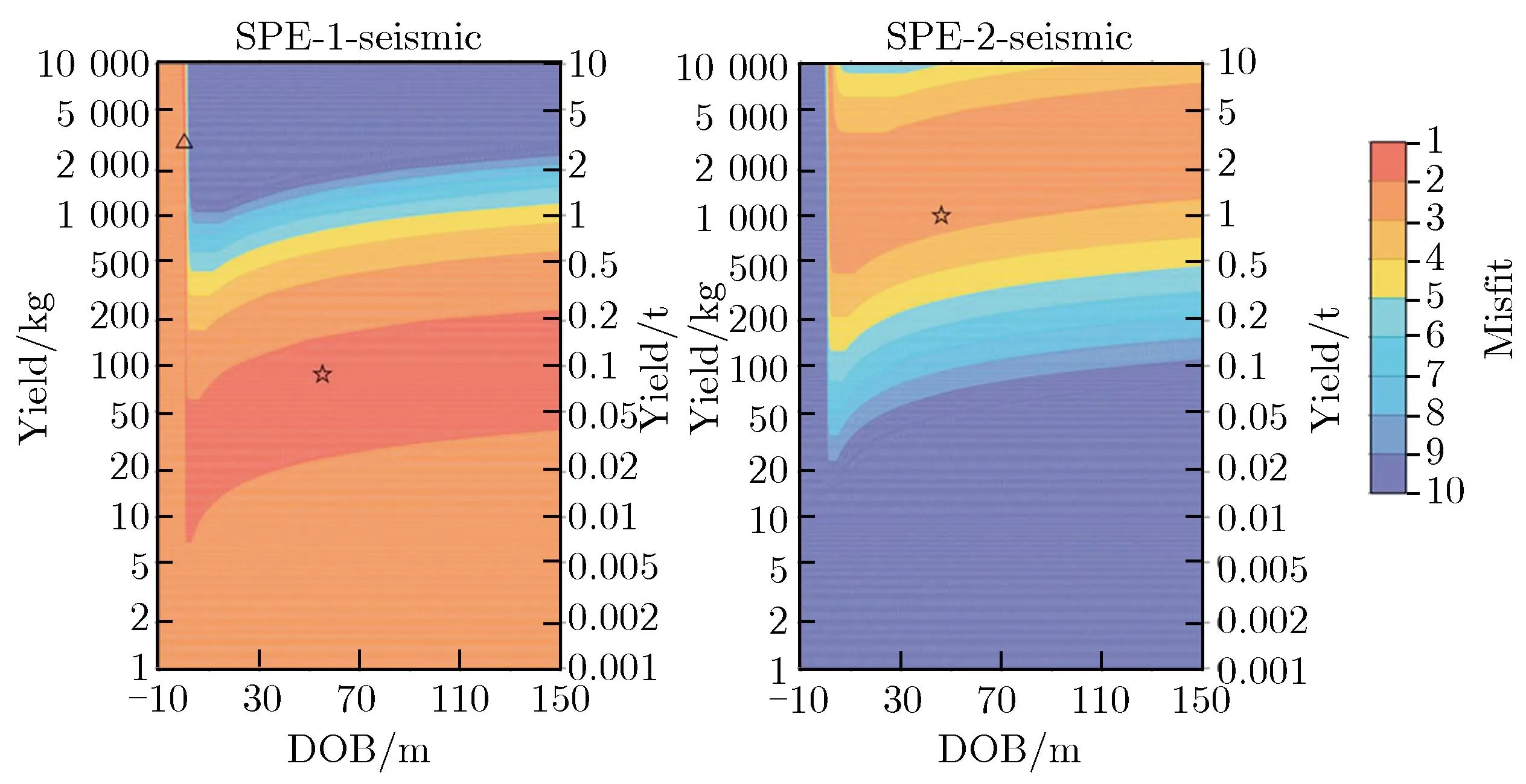
采用声学数据或地震波数据对源参数进行反演,当量和爆高(埋深)之间通常会存在明显的折中关系使求解不适定。而声震分析方法通过融合地震波(地运动)数据和声学(空气超压)数据使得反演问题变得适定,从而得到当量和爆高(埋深)估计值。图14为典型试验 (FSE-4) 的折中关系和声震分析结果[24]。图14中,五角星为真实值,空心三角形为地表处的最优点,实心三角形为整个区域的最优点。

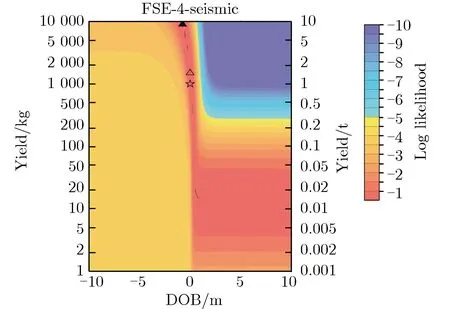
(a)Results by seismic data

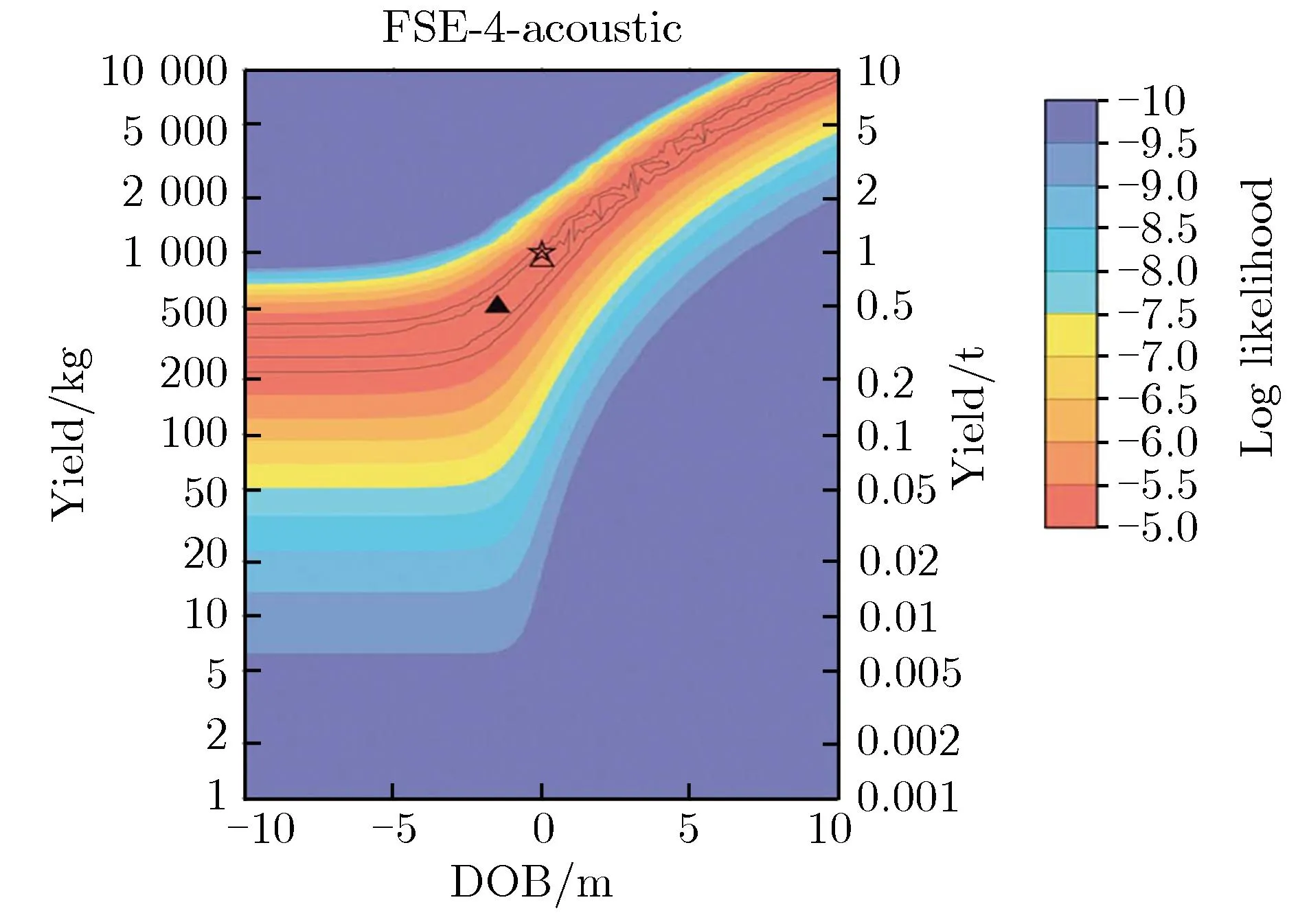
(b)Results by acoustic data

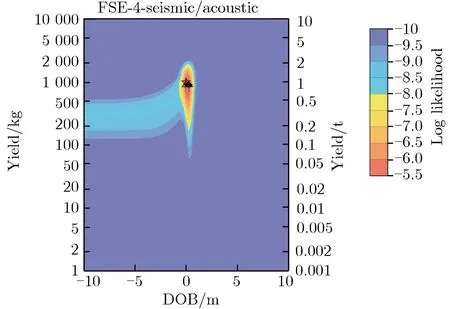
(c)Results by seismic and acoustic data

声震融合算法是声震分析的关键组成,随着声震分析方法的不断改进,声震融合算法从相对偏差法[22]、对数偏差法[23]及折中曲线交叉法[23]到似然函数法[24]和贝叶斯MCMC方法[25-26, 48]再到机器学习方法[27],得到了不断发展。表4为数据融合算法特点和计算公式。

表4 数据融合算法特点和计算公式

图15为不同数据融合方法的典型反演结果。表4列出的前4种方法没有考虑模型参数的先验信息,源参数缺少进一步约束,且计算采用格点搜索法,效率较低。贝叶斯马尔可夫链蒙特卡罗 (Markov chain Monte Carlo,MCMC)方法[25-26, 48]同时考虑了偏差信息和先验信息,采用统计的方法对爆源参数进行估计可给出更合理的统计解释,同时采用MCMC方法获得较高的求解效率。Johannesson等[48]给出了声震融合的贝叶斯MCMC反演框架,Zhang等[25]和Ford等[26]进一步发展了该方法,基于MCMC方法求解源参数,并应用于近地面爆源参数估计。图16为贝叶斯MCMC方法求解流程。以上数据融合方法基于已有的声震模型反演爆源参数和不同场地岩土类型具有不同的声震模型。数据融合方法的反演精度和声震模型密切相关。研究表明[42, 45],声震模型和场地条件的不匹配将导致较大的反演偏差。为减小因声震模型匹配程度带来的反演偏差,提高反演模型在不同场地的适用性,Stroujkova等[27]采用人工神经网络(artificial neural network,ANN)和贝叶斯正则化方法融合小样本声震数据来估计当量和爆高(埋深),尝试将机器学习算法应用在爆源参数反演。图17为基于深度学习的爆源参数反演流程。

(a)Method of relative deviation[22]

(b)Method of logarithmic deviation[23]

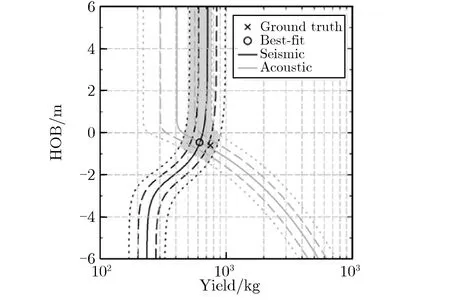
(c)Tradeoff curve crossing method[23]

(d)Likelihood function method[24]

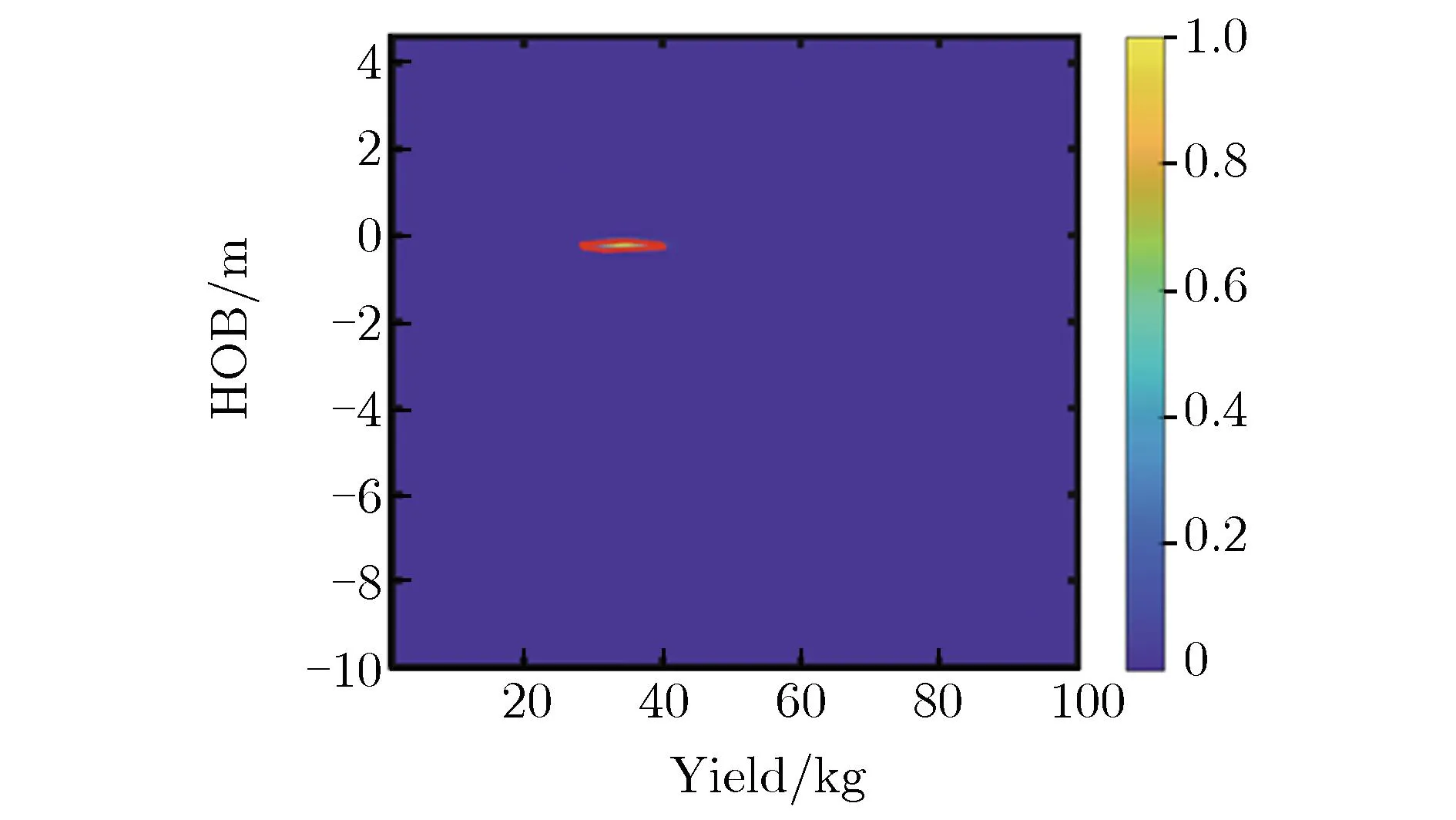
(e)Bayesian MCMC method[25, 26, 48]

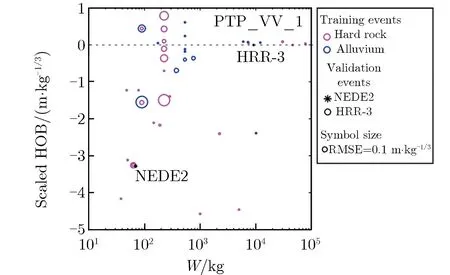
(f)Machine learning method[27]

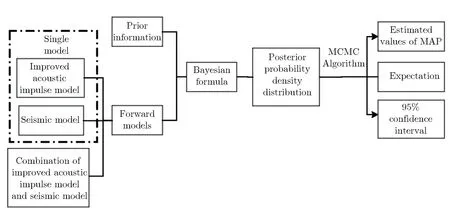
图16 贝叶斯MCMC方法求解流程[25]

图17 基于深度学习的爆源参数反演流程[27]

4 总结与展望

经过十几年的研究,发展了多种近地面声学模型和地震波模型,适用冲积土、沙土、沉积岩、花岗岩和土石混合体等多种地质条件,联合相对偏差法、折中曲线交叉法和贝叶斯MCMC等数据融合算法,或基于声震数据采用机器学习方法,可有效解决多种场地近地面爆源的爆炸当量和爆高(埋深)反演问题。声震分析方法虽得到了快速发展,但还需重点解决以下问题：

(1)近区声/震模型修正完善。受到场地条件限制,不同地质、不同爆高和不同距离的声震数据有限,还需更多的试验数据对近地面声/震模型进行补充、修正和完善,从而获取适用不同地质成分的通用模型。目前,声/震数据主要通过外场试验获取,需进一步发展基于微药量化爆模拟及超重力离心机等平台的实验室模拟技术。

(2)远区声/震模型快速建模。区域较大时,受地质地形和大气环境等因素的影响,近地面爆炸耦合的地震波和声波表现出复杂的传播特性,给远区爆源参数快速准确反演带来了巨大挑战。目前,声震分析技术以近区为主,需进一步发展大区域快速建模技术,实现远区爆源参数的快速准确反演。

(3)基于机器学习的快速反演方法。机器学习可有效解决数据融合和快速计算问题,但该方法在声震分析应用较少,需基于机器学习算法,进一步发展小样本声震数据反演技术及基于物理机制的大区域爆源参数反演技术。

(4)未知爆源位置的声震分析方法。目前声震分析研究是在爆源位置已知条件下开展的,未考虑爆源位置估计偏差的影响,需进一步开展基于声震数据的爆源位置、当量和爆高(埋深)的综合反演方法研究。可通过贝叶斯MCMC或机器学习方法建立爆源多参数的综合反演框架。