新课标视域下尺规作图学材思考
文|林志辉 陈柯柯
一、课改过渡期面临的学力尴尬
1.学习内驱力不足
尺规作图是指通过借助没有刻度的直尺和圆规进行有限次画图,可学生明明用刻度尺、量角器等测量工具就可以快速解决问题,利用尺规作图反而增加了学习难度。
2.教学知识序紊乱
现在使用的教材编排和新课标相关尺规作图的知识内容分布存在着出入。
面对课改期间的学力尴尬,该如何激活学生探索的兴趣,还有哪些内容可以加强探索?笔者通过本文尝试提出破解课改过渡期间困境的学材,以供同行参考。
二、适配过渡期的学材探索
小学阶段的尺规作图有别于初中的尺规作图,侧重于加深学生对图形特征的理解,激发学生的学习兴趣和创造力,培养学生的几何直观和推理意识。在尺规作图教学前,明确适配学生现行知识点编排顺序的教学内容是不可或缺的。为此笔者进行了“小初”尺规作图的共性内容对比梳理,尝试发掘更多的知识载体,通过系统的序列推进,进行适配过渡期的尺规作图通盘设计。
1.共性“小初”知识罗列
《义务教育数学课程标准(2022年版)》中安排了三个课例说明尺规作图的教学建议,对照初中的尺规作图的五个基本作图,笔者发现小学的例26 和例29通过作等长线段和通过作图认识三角形周长对应着初中的“作一条线段等于已知线段”。例32 侧重借由尺规作图理解三边关系,作一个相同的三角形对应初中的“作一个角等于已知角”。如张丹教授团队的研讨课中,学生在探究三边关系中,经历探索尝试到用尺规作已知三边的三角形,既感悟了三边关系又渗透了稳定性,充分尊重了学生的认知水平。
2.增性“尺规”内容梳理
《义务教育数学课程标准(2022年版)》中尺规作图看似内容前移,实则是丰富学生的经验感悟,正如核心素养的螺旋培养一样,小学阶段着重意识,初中阶段着重观念,而到了高中才是走向能力的培养。尺规作图也一样,笔者理解并不是单纯的知识前移,而是在学有余力的前提下,让学生进一步理解图形的特征,感悟数学的魅力,积累丰富的经验。小学阶段除了提及的这三个课例,是否还有其他可以探索尺规作图的知识载体呢?初中的另外三种基本作图学生是否也可以尝试呢?
(1)过渡增加:菱形
学生既然会尺规作三角形,那么尺规作四条边都相等的四边形(菱形)是否也可以尝试?菱形虽然是初中的教学内容,但小学生并不陌生,不揭示其本质属性仅以四边形视之,菱形其实是很好的尺规作图感悟素材。菱形隐含着四边形可以分成两个三角形的知识,学生用尺规作菱形可以分成两个以AB 为底的等边三角形(如图1 左所示),学生还可以以线段AB 为腰,作两个等腰三角形(如图1 中所示),而这样的点C和点D 可以有无数组,学生在画的过程中感受四边形的不稳定性,进一步对比加深对三角形稳定性的感悟(如图1 右所示)。
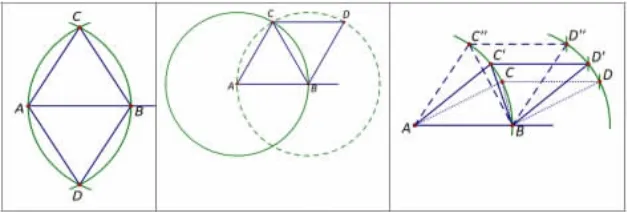
图1 以线段AB 为底作菱形(左)以线段AB 为腰作菱形(中)感悟四边形的不稳定性(右)
(2)拓展增加:角平分线和垂线
有了画菱形的经验,学生对于第四个点的形成具备一定的作图经验和感悟,画角平分线时自然而然迁移了画法经验,如图2左所示,画四条边相等的四边形,此时通过连接线段OC,说明三角形OCB 和三角形OAC 一样大,所以∠BOC 和∠COA 是一样大的。又可如图2 右所示,不拘泥于四条边都相等,作线段BC 等于线段AC,获得两个一般性的三角形OCB 和三角形OAC。但究其本质学生都是在迁移尺规作图两个等腰三角形OAB 和三角形ACB。角平分线看似是初中的知识,但小学生借由小学阶段的知识和经验也是可以初步感悟的,这样的感悟又丰厚了对四边形和三角形的特征理解。
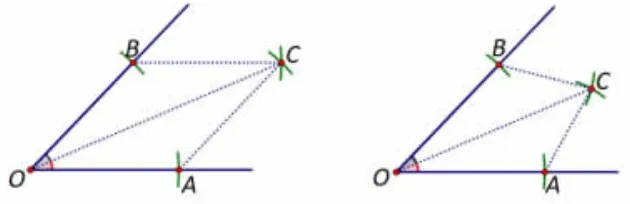
图2 角平分线的尺规作图(左)角平分线的尺规作图(右)
众所周知,尺规作图的实际应用中垂径定理是被高频使用的,但是小学生对于垂径定理确实存在很大的难度,笔者思考是否可以基于角平分线的基础,引导学生将直线看成平角,如图3所示,作线的垂线。聚焦这样的垂线作图,学生也是用尺规作三角形的方法推进,在方法经验的迁移下,感悟垂直作图的过程,拓宽学生的知识边界,将知识进行关联化的融通。

图3 尺规作图——垂线
三、基于实证性的通盘设计
基于可以尝试拓展的尺规作图内容,聚焦学生的知识、经验起点,将尺规作图的教学安排在六年级学习完《圆的认识》单元之后,如表1所示。笔者串联设计三课时,基于简单的学材,通过序列的螺旋推进,带领学生经历尺规作图,丰厚图形认识,通过描述、刻画的互译发展学生的几何直观,在综合运用知识的情况下,感受数学知识之间的联系,体会理性思维的魅力,激发数学学习的兴趣。
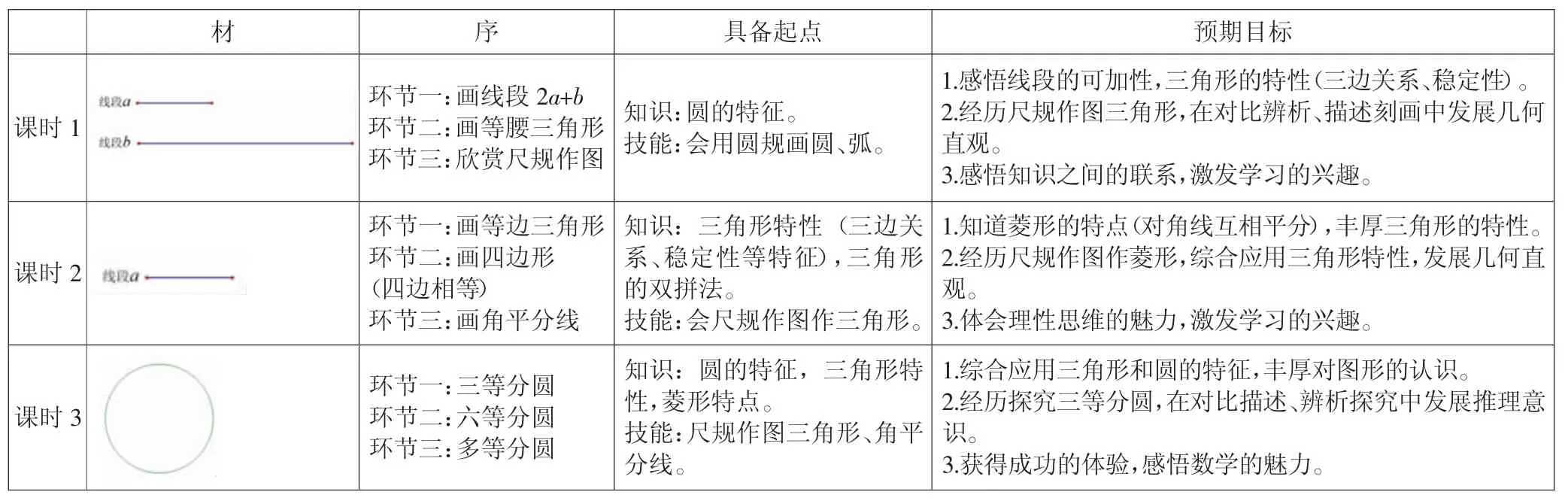
表1 尺规作图课例表
三节课皆是围绕着尺规作图三角形,不增加学生的知识难度,串联学生小学阶段的图形知识,如课时1 聚焦简单的两条线段,通过画线段的累加和等腰三角形,因为素材的巧妙设计(2a<b),感悟只能以线段a 为底,感悟三角形的三边关系,又在对比不同位置的摆放中感悟三角形的稳定性。课时2 通过画四条边都相等的四边形进一步感悟三角形的特征,理解三角形的双拼法和四边形的不稳定性。课时3 通过画三等分圆、六等分圆和多等分圆进一步融会贯通图形特征的感悟。
尺规作图在小学的引入是学生理解图形特征很好的载体,但笔者建议要求不宜过高,不必进行严格论述每一步的作图方法,只要能清晰说明自己的方法,在感悟为什么可以这样作背后的道理就可以。

