考虑地连墙槽段接缝影响的竖井应力和变形规律研究

吴国诚 周跃峰

摘 要：由地下连续墙（简称“地连墙”）筑成的圆形围护结构径向变形小，在竖井工程中得到广泛应用，但在计算中如何合理考虑其环向效应是亟待解决的科学问题。为揭示地连墙槽段接缝泥皮对圆形超深竖井应力变形的影响，在某输水隧洞超深竖井数值分析中，采用实体单元模拟地连墙Ⅰ、Ⅱ槽段接缝泥皮，并在地连墙-岩土、混凝土衬砌-地连墙、地连墙-缝间填充物之间均设置接触面，对泥皮缝宽、材料特性进行了参数敏感性研究，获得了竖井支护结构的受力特征。结果表明：地连墙受力以竖向应力与竖向弯矩为主，随缝宽的减小或者缝模量的提高，地连墙的径向位移、竖向弯矩与竖向压力均减小，而环向压力增大；在开挖至土岩交界面时地连墙径向位移与竖向弯矩最大，开挖至坑底时环向弯矩最大。圆形衬砌受力以环向为主，其与地连墙受力方向互补，弥补了地连墙槽段接缝泥皮的环向削弱作用。研究成果可为竖井的设计优化与施工提供技术支撑。

关键词：地连墙；槽段接缝泥皮；超深竖井；环向效应；接缝非线性

中图分类号：TU473                                             文献标志码：A

0 引 言

竖井支护是为了保证地下结构施工及基坑周边环境的安全，对竖井侧壁及周边环境所采取的支护措施，支护方法有很多种，如地下连续墙、排桩、土钉墙、水泥土墙等。针对竖井施工过程中各类支护结构与岩土体的共同作用机制，学者们开展了广泛的研究[1-7]。Kirkbride等[2]采用岩土弹塑性理论分析了竖井侧壁围岩的应力分布状态。Guz[3]采用理论分析与试验验证相结合的方法，分析了竖井施工过程中的围岩变形机制，提出了竖井围岩稳定性评价方法。陈恩瑜等[4]针对陡倾不良地质条件下大型调压竖井开挖支护问题，进行了方案比选与优化设计。李孟等[5]采用连续体板单元模拟地下连续墙，通过数值分析方法研究了不良地质条件下竖井的围岩稳定性、支护结构的变形与受力规律，提出了对围岩变形进行有效控制的措施。鲍利发等[6]通过数值分析方法研究了抽水蓄能电站深厚覆盖层中大断面土质竖井的围岩稳定性，从支护设计和开挖方案两方面综合采取措施，对围岩变形进行有效控制。过江等[7]针对冰碛土层中竖井采取的锚喷联合支护结构进行了受力变形分析，对比分析了不同施工方法的实施效果。

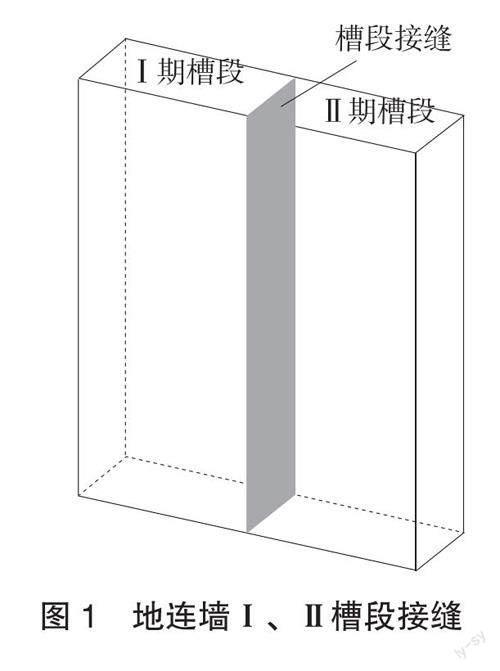
地下连续墙作为竖井的一种常见支护结构，是在地面上采用挖槽机械，在泥浆护壁条件下，开挖出一条狭长的深槽，在槽内吊放钢筋笼，然后用导管法灌筑水下混凝土筑成一个单元槽段，如此逐段筑成一道连续的钢筋混凝土墙壁[8]。由地连墙筑成的环形围护结构拱效应强烈，可以有效控制径向变形，采用环形地连墙的竖井支护案例不断增多[9]。地连墙的槽段混凝土常采用分期浇注，由于采用泥浆护壁，Ⅱ期槽段浇注时，在Ⅰ、Ⅱ期槽段间必然存在一定厚度的接缝泥皮[10]（见图1）。根据其受力特性可分为不抗弯不抗剪柔性接缝、抗剪不抗弯半刚性接缝以及抗剪又抗弯刚性接缝3种[11]。地下连续墙应力和变形的空间效应与槽段接头的力学特性紧密相关，在数值计算中合理考虑接缝作用是亟待解决的科学问题[12]。

环形地连墙环向刚度受槽段接缝刚度[13]、接缝数量和半径大小有关[14]，目前工程中尚无成熟的确定方法。早期将地连墙简化为单根梁，得到的墙体内力与实际相差较大。目前采用考虑圆形拱效应的平面竖向弹性地基梁法，在计算墙体的等效分布弹性支撑系数时引入了考虑槽段接头效应的环向刚度修正系数a，并建议a取0.4～0.7[15]，但a值与地连墙接缝的接头类型、施工工艺水平密切相关，如何定量取值并无定论，仅凭经验确定。裴颖洁等[16]采用二维有限元模型建立了地下连续墙与接缝的简化模型，研究了墙体水平位移以及支护体系受力特征受连续墙接头型式的影响规律。陈富强等[17]采用弹性理论的方法研究了地下连续墙接头的数量、槽段夹泥和三种接头作用效应的具体差异。当前，关于环形地连墙的接缝对于竖井支护体系影响的研究成果仍鲜有报道。

1 圆形超深竖井地连墙接缝设计

某输水隧洞超深竖井采用地连墙、内衬砌、冠梁等相结合的支护形式，该竖井深度83.5 m，直径31.6 m，地连墙厚1.2 m，内衬采用变截面厚度，在-7.5 m高程以上厚度为1.2 m，-7.5m高程以下厚度为1.5 m。冠梁尺寸为2.7 m×3.0 m，位于竖井顶部。工作井地连墙一期槽段长6.8 m，二期槽段长2.8 m（一、二期搭接0.4 m），一期槽、二期槽均为13幅，槽段设计见图2。

为探讨地连墙槽段接缝泥皮对竖井应力变形的影响，采用实体单元模拟地连墙Ⅰ、Ⅱ槽段接缝泥皮，设定0、2、4 cm三种缝宽，考虑缝间填充物软硬程度，并在地连墙-岩土、混凝土衬砌-地连墙、地连墙-缝间填充物之间均设置接触面，获得多个方案竖井支护结构的受力特征，为竖井的优化设计与施工提供技术支撑。

2 数值分析模型及计算步骤

有限差分数值模型如图3所示。模型包括108 328個单元、101 641个节点。模型的水平方向设定为X向与Y向，竖直向为Z向。模型长度、宽度均为150 m，超过竖井直径4.5倍；模型总高度140 m，底部边界距离竖井底部约60 m。模型四个侧向边界上施加法向约束，模型底边界施加三向固定约束。

施工期的竖井地下水位施加于模型顶面，土体范围内采用土水分算考虑地下水的静水压力作用。在地下水位以下的岩土层与地连墙交界处施加水压力，以模拟地下水对于基坑施工的环境影响。土体材料模型选取摩尔-库伦模型，衬砌混凝土结构采用弹性模型，计算参数见表1。

根据施工流程（见表2）模拟竖井开挖的全过程及其对周边环境的影响。利用软件中单元的“生死”功能模拟竖井工程地连墙施工、各层土体的开挖以及冠梁和衬砌的施工过程，计算得到地连墙、衬砌结构的应力变形以及竖井外侧地表的变形情况。计算方案见表3。其中，缝间填充物为“软”时填充材料按砂土考虑，性能参数参考文献[18]取值；填充物为“硬”时填充材料按水泥砂浆考虑，性能参数参考文献[19]取值；填充物为“中”时填充材料按砂土和水泥砂浆混合考虑，参数取值按照前两者的数量级取中值。各接触面按照摩尔-库伦准则进行简化，地连墙-缝间填充物之间摩擦系数参考同类计算实例取值为0.3。

3 竖井支护结构内力与变形统计

表4、表5分别为地连墙、衬砌与冠梁各方案内力与变形统计值。以强风化层底部为土岩交界面进行分析，距地表深度约为31 m。各方案的地层水平变形差异小于5 mm，沉降变形差异小于20 mm，缝宽4 cm软缝，开挖分节5 m时最不利，竖井沉降如图4所示。开挖至土岩交界面，地层水平变形最大值18.0 mm，地层沉降量最大值65.7 mm。开挖至坑底，地层水平变形最大值22.0 mm，地层沉降量最大值81.5 mm。

4 地连墙内力与变形分析

根据材料力学方法，将地连墙应力换算成对应的弯矩与轴力[20]。

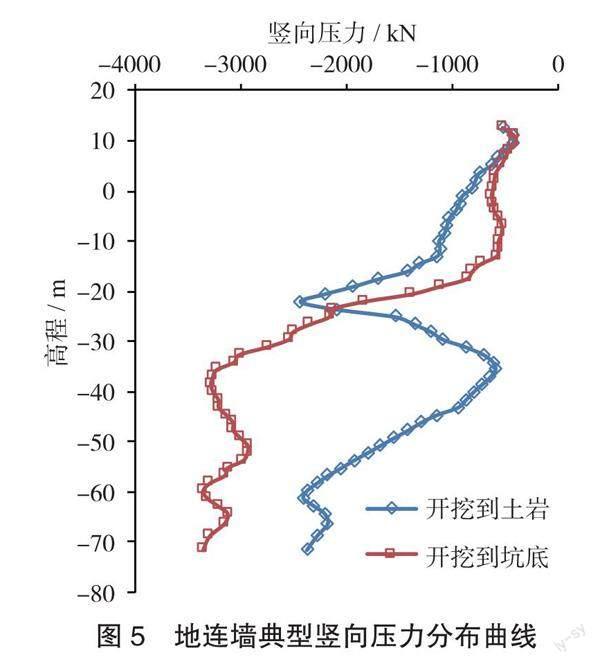
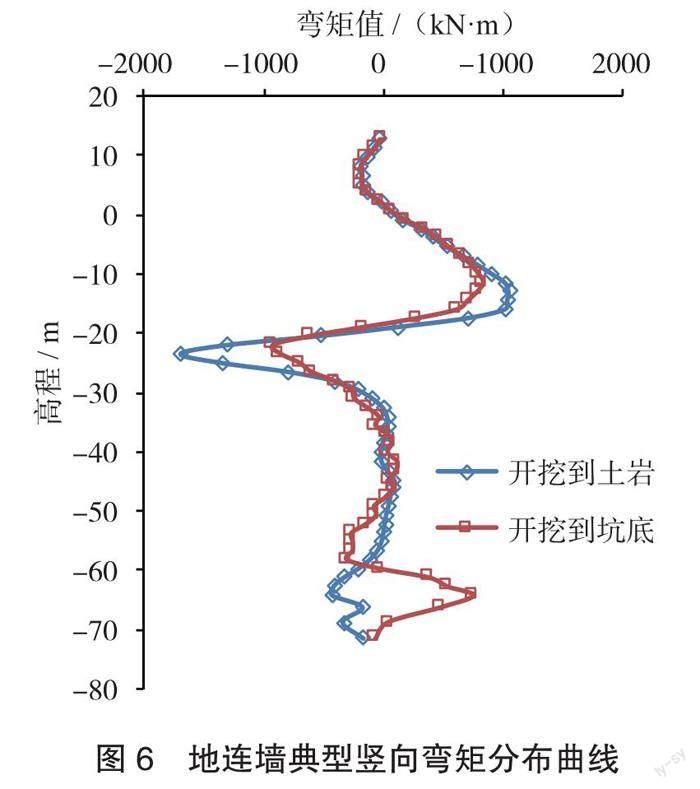
由于地连墙Ⅰ、Ⅱ期槽段之间有缝，其受力以竖向压力与竖向弯矩为主，图5与图6分别为地连墙典型竖向压力与竖向弯矩曲线。地连墙最大竖向拉应力发生在开挖至土岩交界面时，为2.6MPa，分布在土岩交界范圍地连墙外侧；地连墙最大水平向压应力为-10.3MPa（图5）。换算得到的各方案地连墙最大竖向弯矩为1 687 kN·m（图6），发生在开挖至土岩交界面时；最大环向弯矩为697 kN·m，发生在开挖至坑底时。地连墙开挖至坑底时最大竖向压力为-10 864 kN，最大环向压力为-14 493 kN（硬缝时）。

对比不同方案计算结果可知，随着缝宽的减小，地连墙的径向位移、竖向弯矩与竖向压力均减小，而环向压力增大。随着接缝弹性模量的提高地连墙的径向位移、竖向弯矩与竖向压力均减小，而环向压力增大。开挖分节对主要影响地连墙的径向变形，开挖到土岩交界面时，开挖分节3 m与分节5 m地连墙径向位移分别为7.2 mm与8.2 mm，而开挖到坑底时地连墙径向位移分别为17.7 mm与21.7 mm。分节5 m时地连墙的弯矩与压力相对较大，但与分节3 m时相比无明显差异性。

5 衬砌内力与变形分析

衬砌采用结构单元模拟，各方案衬砌径向位移开挖至土岩交界面时最大值为1.0 mm，开挖到坑底时最大值为7.6 mm，均小于地连墙径向位移。各方案环向弯矩、竖向弯矩、竖向压力、环向压力最大值均出现在开挖至坑底时。

对比不同方案计算结果可知，随着缝宽度的减小，衬砌的径向位移、环向弯矩、竖向弯矩、竖向轴力、环向轴力均减小。随着缝模量的提高，衬砌的径向位移、环向弯矩、竖向弯矩、竖向轴力、环向轴力均减小。开挖分节对衬砌的变形影响不大，但对衬砌的环向弯矩、环向轴力影响较大。

6 冠梁内力与变形分析

冠梁的受力与缝宽紧密相关，缝宽4 cm时冠梁为拉力，缝宽0 cm时冠梁为压力。开挖至坑底后，各方案冠梁径向位移最大值约0.9 mm，轴向拉力最大值为2 245 kN，轴向压力最大值为-441 kN。最大竖向弯矩为1 241 kN·m，最大环向弯矩为

846 kN·m。

对比不同方案计算结果结果可知，随接缝宽度的减小，冠梁的径向位移、竖向弯矩、环向弯矩均减小。随着接缝弹性模量的提高，冠梁的拉力、径向位移、竖向弯矩、环向弯矩均减小。开挖分节对冠梁受力没有明显的影响。

7 与规范计算结果对比

取单位宽度的墙体作为竖向弹性地基梁，根据《港口工程地下连续墙结构设计与施工规程》

（JTJ 303—2003）[21]附录C及《公路桥涵地基与基础设计规范》（JTG 3363—2019）[22]附录T，墙体环向效应及内衬的作用以等效支撑弹簧来替代计算（见图7）。考虑施工过程，采用基坑支护设计计算软件“理正深基坑”进行计算。

采用规范计算得到的正常运行工况地连墙弯矩最大值为2 256 kN·m，剪力最大值为1 150 kN；衬砌结构规范算法[20]弯矩最大值为1 864 kN·m，轴力最大值为9 810 kN。与数值计算得到的表4与表5对比，可知数值计算与规范法得到的地连墙与衬砌内力最大值大小基本相当，说明本文提出的计算方法能够反映地连墙槽段接缝对内力的影响。

8 结 论

针对某输水隧洞超深竖井，结合实际设计的地连墙、衬砌、冠梁等支护体系，建立三维数值模型，开展地连墙槽段接缝泥皮参数敏感性分析研究，得到如下结论。

（1）由于地连墙Ⅰ、Ⅱ期槽段之间有接缝泥皮，其受力以竖向应力与竖向弯矩为主。随接缝宽度的减小或者随着缝模量的提高，地连墙的径向位移、竖向弯矩与竖向压力均减小，而环向压力增大。

（2）地连墙最大竖向弯矩发生在开挖至土岩交界面时，最大环向弯矩发生于开挖至坑底。

（3）衬砌作为一个环向的整体，其受力以环向为主，其与地连墙受力方向互补，弥补了地连墙槽段接缝泥皮的环向削弱作用。

（4）冠梁的受力与接缝宽度紧密相关，缝宽4 cm时冠梁为拉力，缝宽0 cm为压力。

参考文献：

[1] 骆晓锋，邱伟，杜小凯，等. 竖井土质围岩综合力学参数反演及稳定性预测[J]. 人民长江，2021，52（增刊1）：296-300.

[2] KIRKBRIDE M，STRINGER N. Ultra-deep Shaft Construction[J]. Tunnels and Tunnelling International，2002，34（6）：38-40.

[3] GUZ A N. Establishing the Fundamentals of the Theory of Stability of Mine Workings[J]. International Applied Mechanics，2003，39（1）：20-48.

[4] 陈恩瑜，张宏山，彭会椿. 陡倾不良地质条件下大型调压竖井开挖支护施工[J]. 人民长江，2014，45（1）：69-72，81.

[5] 李孟，鄭月昱，杨小平，等. 深厚砂层深挖圆形竖井施工数值模拟及实测分析[J]. 地下空间与工程学报，2017（5）：1355-1362.

[6] 鲍利发，余雪松，吴喜艳，等. 深厚覆盖层中大断面竖井开挖支护设计[C]//抽水蓄能电站工程建设文集，2021：151-154.

[7] 过江，蒋倪明，程鑫. 富水冰碛层竖井施工过程数值模拟[J]. 黄金科学技术，2022，30（5）：733-742.

[8] 李学聪. 复杂地层地下连续墙施工关键技术[J]. 施工技术（中英文），2021，50（16）：38-41.

[9] 徐前卫，龚振宇，孙梓栗，等. 滇中引水工程超深圆形基坑施工变形和内力监测结果分析[J]. 土木工程学报，2022，55（6）：102-111.

[10] JTG 3363—2019，公路桥涵地基与基础设计规范[S]. 北京：人民交通出版社，2019.

[11] 诸以惇，陈卫忠，田洪铭，等. 考虑连续墙接头效应的软土大型盾构工作井稳定性分析[J]. 岩土力学，2011，32（10）：2937-2943，2950.

[12] 徐中华，李靖，翁其平，等. 超深圆形基坑计算分析方法及工程应用[J]. 施工技术（中英文），2022，51（1）：13-20.

[13] GUNN M J，CLAYTON C R I. Installation Effects and Their Importance in the Design of Earth-Retaining Structures[J]. Geotechnique，1992，42（1）：137-141.

[14] POWRIE W，KANTARTZI C. Ground Response during Diaphragm Wall Installation in Clay：Centrifuge Model Tests[J]. Géotechnique，1996，46（4）：725-739.

[15] 崔剑峰，胡建华，贺炜，等.圆形地下连续墙的环向刚度折减效应及修正方法研究[J]. 岩土工程学报，2017，39（11）：2132-2138.

[16] 裴颖洁，郑刚，刘建起. 两侧铰接地下连续墙的试验研究及数值分析[J]. 岩土力学，2008，29（1）：279-284

[17] 陈富强，杨光华，张玉成，等. 圆形地下连续墙结构设计中α系数取值探讨[J]. 岩土工程学报，2012，34（增刊1）：203-206.

[18] 顾晓鲁，钱鸿缙，刘惠珊，等. 地基与基础（第二版）[M]. 北京：中国建筑工业出版社，1993.

[19] 高鹏鹏，路永华，黄昭，等. 轻质聚合物水泥砂浆弹性模量的研究[J]. 建筑技术开发，2012，39（1）：22-24.

[20] 姚长春，于海龙，张洋. 基于FLAC3D软件求解衬砌强度安全系数的方法[J]. 四川建筑，2007（2）：115-116.

[21] JTJ 303—2003，港口工程地下连续墙结构设计与施工规程[S]. 北京：人民交通出版社，2004.

[22] CECS 137—2015，给水排水工程钢筋混凝土沉井结构设计规程[S]. 北京：中国计划出版社，2015.

Stress and Deformation Patterns of Vertical Shafts Considering the Effect of Grooved Section Joints of Diaphragm Walls

WU Guocheng1，ZHOU Yuefeng2，3

（1. Shenzhen Water Engineering Construction Management Center，Shenzhen 518036，China；2. Key Laboratory of Geotechnical Mechanics and Engineering of the Ministry of Water Resources，Changjiang River Scientific Research Institute，Wuhan 430010，China；3. National Dam Safety Engineering Technology Research Center，Wuhan 430010，China）

Abstract：Circular enclosure structures made of diaphragm walls are widely used in shaft construction due to their low radial deformation. However，it remains an urgent scientific problem to reasonably consider its loop effects in calculations. This study aims to reveal the influence of the joint skin of the groove section of the diaphragm wall on the stress and deformation of circular ultra-deep shaft. A solid unit was employed to simulate the joint skin of Ⅰ and Ⅱ groove sections of the diaphragm wall in the numerical analysis of an ultra-deep shaft in a water conveyance tunnel. Moreover，contact surfaces were established between diaphragm wall and rock and soil，concrete lining and diaphragm wall，and also  between diaphragm wall and interseam fill. A parametric sensitivity study was conducted to investigate the width of mudskin seams and material properties. Numerical modeling results show that the stress and bending moment of the diaphragm wall are mainly in vertical direction. As excavation progresses to the soil-rock interface，the diaphragm wall experiences the largest radial displacement and vertical bending moment. At the pit bottom，the circumferential bending moment reaches peak value. The load direction of circular lining in the top-down method is in the circumferential direction，which is complementary to the stress direction of the diaphragm wall，compensating for the circumferential weakening effect caused by the joint mud skin in the trench section of the diaphragm wall. The research results provide technical support for optimizing the design and construction of ultra deep shafts.

Key words：diaphragm wall；joint mud skin of trench section；ultra deep shaft；circumferential effect；nonlinearity of slot joint

收稿日期：2023-06-05

基金项目：国家自然科学基金项目（51979010）

作者简介：吴国诚，男，高级工程师，硕士，主要从事城市水网工程研究及建设管理工作。E-mail：158597438@qq.com

通信作者：周跃峰，男，正高级工程师，博士，主要从事水工岩土力学与工程研究。E-mail：zhou.yuefeng@163.com