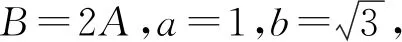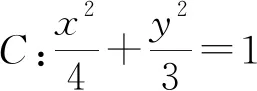研磨经典问题,寻根拓展提升
——以一道数学质检试题为例
卢燕霞
福建省龙岩市教育科学研究院 (364000)
1 试题析解
(龙岩市2022年高三3月质检第20题)记△ABC的内角A,B,C的对边分别是a,b,c,已知a,b,c是三个连续的正整数,且a (1)求a; 分析:本题意图考查解三角形的正弦定理、余弦定理和面积公式,以及三角变换公式等,考查分类讨论思想、函数与方程思想和转化思想,考查逻辑推理、数学运算、数据分析和数学建模等核心素养.本题的亮点在于已知条件“C=2A”,呈现内容丰富,表现在角的动态变化过程,与正、余弦定理有关,也与二倍角公式有关,还与平几知识有关联;第(2)问的“顺时针旋转”也生动刻画了角的旋转,与角的定义产生联系,形成新角,自然地与三角恒等变换有关联. 图1 (i)如图1,sin∠CAD= 图2 高考题的题根,或源于教材,或源于历年真题,或源于数学名题等,从中进行改编、整合.关注试题中的题干“三个连续的正整数”、“C=2A”,可以发现该题源于往年高考试题的加工与整合,在教材中也有背景. 高考题根1 (2021年新高考全国Ⅱ第18题)在△ABC中,角A,B,C所对的边长分别为a,b,c,b=a+1,c=a+2. (1)若2sinC=3sinA,求△ABC的面积; (2)是否存在正整数a,使得△ABC为钝角三角形?若存在,求出a的值;若不存在,说明理由. 高考题根2 (2014年安徽高考理科第16题)设△ABC的内角A,B,C所对的边分别是a,b,c,且b=3,c=1,A=2B. (1)求a的值; 教材题根:(必修5第25页复习参考题B组第3题)研究一下,一个三角形能否具有以下两个性质:(1)三边是连续的三个自然数;(2)最大角是最小角的2倍. 在研磨中,解题是师生努力的共同方向,但经典试题隐藏的价值才是真正的宝库,其中包含了解题思想、数学方法和学科核心素养等育人价值.本文试题中出现的“倍角”,其实也隐藏着一个结论,在往年高考题中频频出现,含金量高,其证明过程涉及丰富的数学思想,极大整合了解三角形部分的知识与方法,具有重要的解题指导意义. 结论在△ABC中,角A,B,C所对的边长分别为a,b,c,且A=2B,求证:a2-b2=bc. 分析:本题关键点是由角的关系转化为边的关系,正弦定理、余弦定理、射影定理和三角函数的定义都具备边角的转化关系;由A=2B可知a>b,角A可能是锐角,也可能是钝角. 证法1:(平几法)巧作辅助线,利用三角形相似得到比值相等获证. 图3 证法5:(定义法)利用三角函数的定义、点的坐标、二倍角公式推理获证.建系往往有简化计算量的功效,具有简洁、优美的特点,因而通过建系写出各顶点坐标,再建立等量关系,化简表达式,得到命题的结论. 图4 说明:本法实质是利用三角函数的定义;此证法是借助点坐标的不同表达,但它们是等量关系;证明过程中的bcosA=c-acosB的本质是射影定理. 倍角关系在解三角形中属于特殊情形,但在高考题中也屡见不鲜,受到命题者的青睐.在解题中若能熟练运用上述结论,就能快速求解有关的边、角问题,准确得到答案(选择、填空题中尤为明显),这里列举若干题,供大家参考. 真题2 (2012年天津高考理科第6题)在△ABC中,内角A,B,C的对边分别为a,b,c,已知8b=5c,C=2B,则cosC=( ). 说明:不仅在三角形中的倍角关系,在圆锥曲线中也有“倍角”关系,而且隐藏了动点的轨迹问题,能通过倍角得到轨迹是双曲线. 此外,2008年四川高考卷文科第7题、2009年湖南高考卷文科第14题、2013年北京高考卷理科第15题等都属于同类型,请读者查阅研究. 探究已知两定点的坐标分别为A(-1,0),B(2,0),动点M满足条件∠MBA=2∠MAB,求动点M的轨迹方程. 高考真题、高质量的模拟题是最好的训练题,是最佳的研磨素材.认真研究经典试题,有利于发现高考命题特点和命题趋势,从中总结规律,探寻解题技巧,研究隐含的思想方法,挖掘相关的变式拓展,便于回归教材,明确考试和复习的方向,更好地驾驭课堂,真正落实“考什么”、“怎么考”、“怎么解”、“为什么这样解”,对培养学生分析问题、解决问题的能力,培养探究意识和批判性思维,培养学科核心素养,提升教育教学质量,都有重要的现实意义.


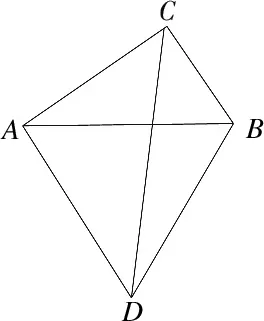

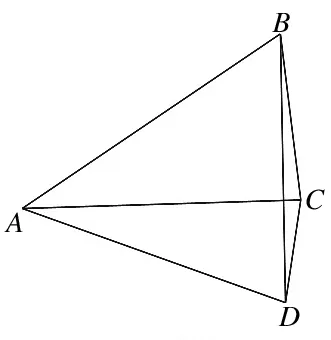

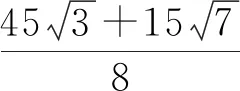
2 题根检索

3 拓展研磨


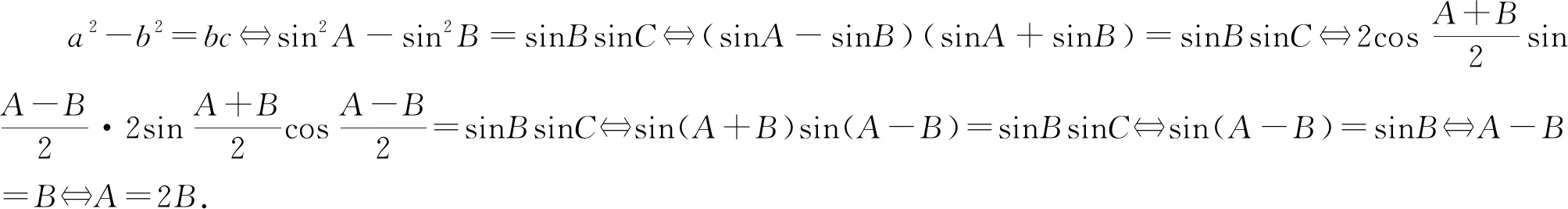

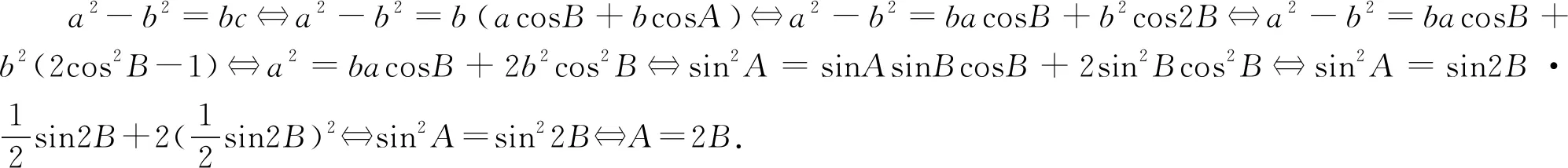
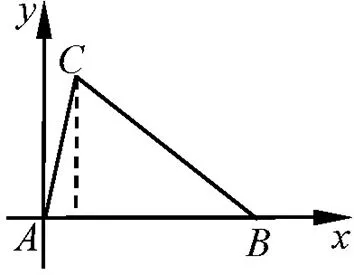

4 拓展应用