面向吊装路径规划的履带起重机运动学建模方法*

康玉伟,陈鹏宇,王 馨,刘 硕,武立波,林远山*

(1.大连海洋大学 信息工程学院,辽宁 大连 116023;2.辽宁省海洋信息技术重点实验室,辽宁 大连 116023;3.大连海洋大学 设施渔业教育部重点实验室,辽宁 大连 116023)

0 引 言

履带式起重机可以垂直升降重物,并进行短距离载物水平运动,满足了重物装卸、运载等作业的系列要求。因其具有灵活的机动性,目前,履带式起重机已经被广泛应用于陆地、海洋、空中等各类建设领域。

履带式起重机的智能化水平主要体现在其运动规划上,因此,有关于履带式起重机的吊装路径规划得到了国内外学者广泛的关注。学者们分别采用A*算法[1]、遗传算法(genetic algorithm,GA)[2,3]、蚁群算法[4]、概率路线图(probabilistic roadmap,PRM)[5]、快速扩展随机树(rapidly exploring random tree,RRT)[6,7]等方法,对起重机的吊装路径进行了规划[8-19],并取得了不少成果。

对履带起重机进行建模是其运动规划的基础和前提。机器人建模即是参考实体机器人的各项参数指标,在计算机仿真平台中,将其进行同比复刻。虽然机器人建模很难做到和实体机器人完全一致,但是它可以抓住被仿对象的关键特征,并利用计算机仿真技术,在计算机上生成具有真实感的仿真环境[20-22],实现对实体机器人的一些关键操作行为进行有效仿真的目的。

履带起重机的运动学模型描述了不同时刻其吊装动作所对应的起重机状态。通常可以利用其运动学模型来预测履带起重机的若干步位形点,并判断该动作是否可行,进而根据自身的动作信息做出相应的规划。

然而,作为进行吊装路径规划的基础,起重机建模并没有得到系统的研究。事实上,对于移动式起重机(如汽车起重机、履带起重机等),在外形、运动特点上与移动式机械臂有许多相似之处,即均有一个可移动的平台和一个可搬运物体的臂架系统,因此,移动式起重机可以看作是一种特殊的移动式机械臂机器人。而移动式机械臂目前已经得到了广泛而深入的研究,包括移动机械臂的建模、路径规划、运动控制等方面,均已取得了丰硕的研究成果,一些研究成果甚至已经被应用到实际的机器人产品中。

但是,这些研究大多数是针对全刚体机械臂,即其移动平台、机械臂的每个连杆和关节都是刚体。

徐文福等人[23]针对空间站遥操作机械臂(SSRMS)型7DOF冗余空间机械臂,提出了逆运动学求解的关节角参数化及臂型角参数化两种方法,同时用仿真算例验证了其有效性。禹超等人[24]针对机械臂腕部有偏置的情形,提出了一种基于虚拟球关节的方法,即用虚拟关节替换腕部的偏置连接,用球腕构成虚拟机械手,并进行了运动学仿真验证。

相比于刚体机械臂,目前针对带柔性连杆移动机械臂的相关研究不多。通过文献检索可以发现,徐秀栋、黄攀峰等人研究了空间绳系机器人和带弹性体的机械臂[25-31]。黄攀峰等人[25]针对空间绳系机器人的轨迹跟踪控制问题,提出了一种基于系绳释放特性的跟踪轨迹协调控制方法。徐秀栋等人[26]针对空间绳系机器人姿态控制失稳问题,提出了一种新姿态容错控制方法,并用仿真方法证明了其有效性。王东科等人[27]针对空间绳系机器人对目标逼近过程中的姿态协调控制问题,设计了一种基于可移动系绳点的姿态协调控制机制。

但是,目前尚未有带绳子柔性杆机械臂路径规划建模与路径规划的相关研究。

为此,针对柔性起升绳在运动过程中需保持竖直并可收缩的这一特性,笔者提出一种新的履带起重机运动学建模方法,即采用虚拟连杆和被动关节对刚柔混合的起升系统进行建模,在此基础上,确定履带起重机的位形空间,进而构建履带起重机的正向运动学和逆向运动学模型,最后通过对几个规划问题进行求解,以验证上述模型的有效性。

1 履带起重机建模

1.1 履带起重机结构与基本动作

作为一种可带载行走的起重运输设备,履带起重机的臂架有多样组合工况,如标准主臂工况、标准固定副臂工况、标准塔式副臂工况及其对应的超起型工况等。

为便于阐述,笔者以超起型主臂工况为例开展研究,如图1所示。

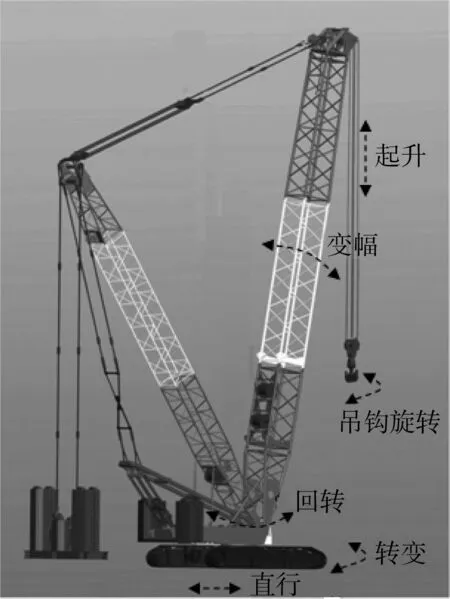
图1 履带起重机的超起型主臂工况

超起型主臂履带起重机主要由下车、转台、臂架、起升绳、吊钩五大部分组成。其中,下车包括两条履带、车架、回转支承(车架与转台的连接件);转台包括转台框架、起升卷扬、发动机;臂架包括主臂、超起桅杆。

而起重机的基本动作有直行、转弯、回转、变幅、起升。其中,行走和转弯是通过两条履带的驱动轮带动履带转动实现的,属于典型的差分驱动。起重机能够在不同曲率半径的圆弧或直线上运动,也能够原地转向,但不能沿着履带的垂直方向运动;回转是通过驱动回转支承旋转的方式实现的,可进行360°回转;变幅是通过变幅卷扬收放变幅钢丝绳的方式实现的;起升是通过起升卷扬收放起升绳方式实现吊钩的升降目的。

需要特别指出的是,整个吊钩分为吊钩滑轮组和吊钩两部分,吊钩是通过活孔与吊钩滑轮组连接的,其可靠人力绕垂直轴360°旋转。在实际吊装时,经常通过人力拨弄被吊物来旋转吊钩,以便被吊物能穿过狭窄的通道。此处,还有另外一个基本动作—吊钩旋转,只不过它不是通过起重机自身动力实现的。被吊物被挂到吊钩上后,履带起重机通过行走、转弯、回转、变幅、起升、吊钩旋转等基本动作,实现被吊物的搬运目的。

1.2 刚柔混合的起升系统建模

在进行刚柔混合的起升系统建模之前,首先要了解起重机吊装过程中的结构和运动特点。吊装过程中,下车、转台、臂架、吊钩等部件变形较小,可认为是刚体。而起升绳为柔性体,在吊装过程中存在以下特点:

(1)起升绳通常为钢丝绳,本身只能受拉不受压,容易出现摆动,但终会在吊钩或被吊物的重力作用下到达竖直状态(稳定静止平衡状态);

(2)柔性的起升绳可以收放(伸缩),实现吊钩升降的目的。

这两个特点是履带起重机与通常的移动机械臂最大的不同,也是建模的重点和难点。下面就对其进行详细讨论,并对其进行建模。

由于起升绳偏摆对起重机的影响比肉眼看到的要严重得多,所以,操作规程通常要求:起吊时起升绳要严格竖直,在吊装过程中要缓慢运动以尽量确保起升绳始终竖直。

另外,在吊装过程中下车、转台、臂架、吊钩等部件变形通常较小。为此,笔者做如下假设:

(1)下车、转台、臂架、吊钩为刚体,吊装过程不发生变形;

(2)起升绳始终竖直,弹性变形忽略不计。

在以上假设基础上,若不考虑运动的具体驱动方式,而仅关注相邻部件的相对运动关系,起重机显然可以采用连杆和关节来描述。具体是把下车、转台、臂架、吊钩滑轮组、吊钩等刚体看作连杆,转台连杆与下车连杆采用竖直轴的转动关节连接,臂架与转台采用水平轴转动关节连接,吊钩采用竖直转动关节连接到吊钩滑轮组上。

与通常移动机械臂不同,臂架到滑轮组该部分需要特别处理:

(1)把起升绳抽象为一个看不见、无形状尺寸的虚拟连杆,其可变长(收放)特性采用移动关节来等效,具体该移动关节坐标系设在起升滑轮组上,移动轴为虚拟连杆坐标系的一轴(具体为-Z轴);

(2)该虚拟连杆采用水平轴转动关节连接,并令该关节变量等于臂架仰角的负值。即臂架变幅关节旋转多大角度,该关节就反向旋转多大角度,以达到起升绳始终竖直的效果。

变幅关节与水平轴转动关节旋转角度关系,如图2所示。

图2 变幅关节与水平轴转动关节旋转角度关系

图2中,起重机臂架在转动一定角度时,起升绳向相反方向旋转。起重机在起吊臂架起吊时刻臂架状态基础上,逆时针旋转γ,此时起升绳为了保证竖直状态,需要顺时针旋转γ,即起升绳从图中虚线处旋转γ到实线表示的状态。总之,该关节与臂架变幅关节形成一种几何约束,令其成为一个被动关节。

根据以上的分析,可得到刚柔混合的起升系统,如图3所示。

图3 刚柔混合的起升系统

图3中的坐标系{i}(i=0,1,…,5)为连杆坐标系,垂直纸面指向读者为X轴、水平方向为Y轴、竖直向上为Z轴。而回转关节的旋转轴为转台坐标系{1}的Z轴;变幅关节的旋转轴为臂架坐标系{2}的Y轴;起升绳旋转关节的轴为虚拟起升绳坐标系{3}的X轴;起升移动关节的轴为起升滑轮组坐标系{4}的-Z轴;吊钩旋转关节的轴为吊钩坐标系{5}(与坐标系{4}重合)的Z轴。

1.3 履带起重机运动学建模

1.3.1 正向运动学

为了简化机器人工作空间的复杂规划场景,LOZANO-PEREZ[32]引入了位形间(C-space)的概念。位形空间由自由空间Cfree和障碍物空间Cobs两部分组成,这样就不需要明确定义障碍物。同时,任何情况下机器人的位形只能用q来表示,位形的维数与C-space的维数一致,连续的位形序列表示路径P。

笔者用1个七维向量q=(x,y,α,β,γ,h,ω)来描述履带起重机的位形,如图4所示。

图4 履带起重机位形(x,y)—起重机下车的坐标;α—下车的方向角,是起重机的履带方向与X轴正向的夹角;β—转台的回转角度,是起重机的上车方向与X轴正向的夹角;γ—臂架仰角;h—起升绳长;ω—吊钩旋转角

根据图3的构型可获得单开环运动链,如图5所示。

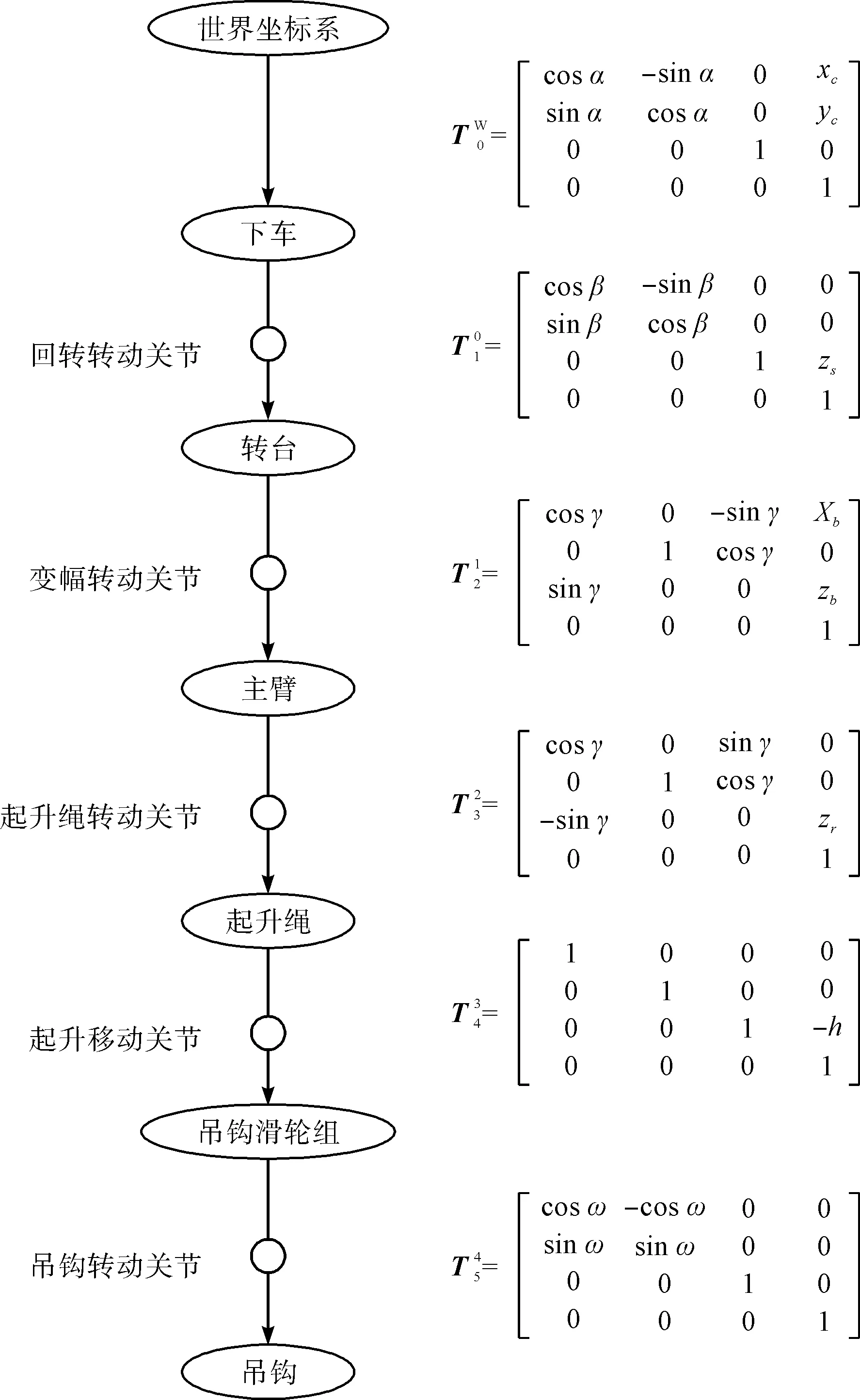
图5 履带起重机运动链

(1)

对于给定的履带起重机而言,zs、xb、zb、zr为已知,其中,zs为转台坐标系相对于下车坐标系在z轴上的偏移量,xb和zb分别为变幅转动关节坐标系相对于转台坐标系在x轴和z轴上的偏移量,zr为起升绳转动关节坐标系相对于变幅转动关节坐标系在z轴上的偏移量,详见图3。因此,一旦已知下车的位置(xc,yc)和方位角α,吊钩的位姿即可由β、γ、h、ω等关节变量求得,即根据式(1)建立关节空间到吊钩工作空间的映射。

将相应的参数代入式(1)可得:

(2)

其中：

cosθh=(cosαcosβ-sinαsinβ)cosω-(cosαsinβ+sinαcosβ)sinω;

sinθh=(sinαcosβ+cosαsinβ)cosω-(sinαsinβ-cosαcosβ)sinω;

t=(yb-zrsinγ)。

根据变换矩阵的特性可知,θh正好是吊钩在世界坐标系下的旋转角,变换矩阵的最后一列为吊钩在世界坐标系下的坐标,因此,吊钩的位姿表达式为:

(3)

下面,笔者将深入探讨下车位置(xc,yc)和方位角α的求解。

如前所述,履带起重机行走和转弯需要满足非完整运动学约束,且因起重机运动局限在平面上,故行走和转弯的运动学模型如图6所示。

图6 行走和转弯的运动学模型XOY—世界坐标系;Or—履带起重机的转弯中心;点P(xc,yc)—起重机的位置坐标;α—履带的方向角(世界坐标系下X轴到正向的角度);vL，vR—左右履带的线速度(vL、vR同向并大小相等时,履带起重机直线行走;当vL、vR反向且大小相等时,履带起重机原地转向;当vL、vR同向并大小不等时,履带起重机以R为转弯半径为进行转向);B—左右履带的轨距

若不考虑履带打滑,则起重机的行走和转弯所满足运动学约束可描述为:

(4)

(5)

在起重机行走和转弯过程中,对式(4)进行积分,即可求得下车的位置P(xc,yc)和方位角α;在此基础上,结合各个关节的变量通过式(3),即可求出吊钩的位姿。

1.3.2 逆向运动学求解

履带起重机的逆向运动学求解,是已知吊钩的位姿反求各个关节变量的值。而履带起重机在实际的吊装过程中,既可以带载行走,也可以下车固定,为此,下面笔者分别对这两种情况的逆向运动学求解进行分析。

(1)下车固定情况

由式(3)可知,根据吊钩位姿可得到4个方程,而下车固定即已知下车位置P(xc,yc)和方位角α,这时式(3)的方程组只剩下4个关节变量未知数,因此,可以唯一解析求得这4个关节变量。其具体步骤是:

首先,根据式(3)中的第1、2方程确定出β,具体见下式:

(6)

接着,把β代入第1个方程,求得γ,具体见下式:

(7)

然后,把γ代入第3个方程进而求得h,具体见下式:

h=zr·cosγ+zb+zs-Zh

(8)

最后,根据已经求得的β以及方位角α和θh确定出ω,具体可见下式:

ω=θh-(α+β)

(9)

(2)下车不固定情况

对于下车不固定的情况,逆向运动学求解则要复杂得多。

从式(3)可知,4个方程存在7个未知数,显然该方程组存在多解,这是因为当允许履带起重机行走时,起重机是一个存在冗余自由度的移动机械臂。而冗余机械臂逆向运动学一般采用数值法,获取其一个或几个可行解,该方法通常需要进行循环迭代。

下面,结合起重机吊装的特点,笔者给出一种逆向运动学的伪解析求解方法。

起重机的主要功用是吊装,因此,给定某臂长某型号的起重机会有一张起重性能表与之对应,这是起重机与机械臂的其中一个区别,该表是一张作业半径(吊钩到回转中心的水平距离)与额定起重量的映射表,表中每一个映射指示起重机在该作业半径下其额定的起升能力是多大。

根据起重机当前吊重和起重性能表,即可确定起重机的最小和最大作业半径。然后,再结合给定的吊钩位姿,即可确定起重机有效的站位范围,并且该范围为一个圆环,称为站位环,如图7所示。

图7 起重机吊装站位环

在此基础上,只要在站位环里随机选择一个点作为起重机的位置,并设定下车的方向,就可以把该逆向运动学问题转化为下车固定的逆向运动学问题,进而逆向运动学问题得到求解。

2 模型在路径规划中的应用

基于上述起重机模型的设计,笔者使用MoveIt中的路径规划来验证其可行性。

下面笔者以快速进行树(fast marching tree,FMT)[33]算法为例,构造3种路径规划,并展示模型在MoveIt下的路径规划,以验证其可用性和有效性。

2.1 起始位形已知的路径规划

一般来说,在起始位形已知的前提下,机器人路径规划问题都可以抽象为:在一个含碰撞区的状态空间中,寻找一条从起始状态到目标状态的无碰撞路径。为了成功构造一条所有位形点都在Cfree,并且它们之间的连接和Cobs无交叉的路径,笔者将履带起重机起吊时刻位形qpicking、就位时刻点位形qplacing和位形空间C输入到运动规划器中,根据选择的算法进行规划。

此处笔者以基于采样的FMT算法为例进行路径规划。一些算法涉及到的概念介绍如下:

(1)采样。即为了从位形空间中随机选择一个位形点,并将其添加到路线图中。如果随机采样的位形点位于自由空间中,则采用;反之,则舍弃,并重新采样。

位形点的产生过程具体为:

(10)

(11)

式中:Δβ,Δγ,Δω—回转、变幅、吊钩旋转的角速度;Δh—起升的线速度;

(2)距离度量。即给定两个起重机位形qi和qi+1,该过程返回一个值,表示从qi到qi+1所需要的代价。具体见下式:

d(qi,qi+1)=|xi+1-xi|+|yi+1-yi|+|r(αi+1-αi)|+
|r(βi+1-βi)|+|(lz(γi+1-γi)|+
|(hi+1-hi)|+|lS(ωi+1-ωi)|

(12)

式中:r—作业半径;lz—臂长;lS—被吊物长。

其中:qi=(xi,yi,αi,βi,γi,hi,ωi)和qi+1=(xi+1,yi+1,αi+1,βi+1,γi+1,hi+1,ωi+1)分别为位形空间中两个位形。

(3)选择邻居节点。该过程用于选择当前位形点的邻居节点。FMT选择基于上述距离度量小于规定的欧几里得距离的位形点作为邻居节点;

(4)局部最优一步连接。对于已经确定的节点x和其所有邻居节点y,该过程尝试在它们之间使用直线路径,忽略障碍物碰撞检测,建立连接;

(5)碰撞检测。这是一个返回值为布尔类型的函数,在连接两个位形点时返回成功或失败。如果连接路径未与Cobs有交叉,则连接成功;

(6)惰性碰撞检测。这是一个优化碰撞检测的操作,在寻找局部最优连接时,算法会忽略障碍物的影响,直接计算各个连接路径的代价值。

FMT-based吊装路径规划的伪代码如表1所示。

表1 FMT-based吊装路径规划

续表

为验证起始位形已知的路径规划的可行性,笔者构建了一个履带起重机吊装案例,如图8所示。

图8 FMT-based吊装路径规划环境搭建

图8中,A为履带起重机起吊时刻位形,B为履带起重机就位时刻位形,要求起重机能够在障碍物环境中,规划出一条能安全地将被吊物从A搬运到B的吊装动作路径。

该案例以利勃海尔的LR1400-2履带起重机作为吊装机器,其工况为标准型,臂长为49 m。笔者调用传统路径规划算法FMT,在验证正向运动学有效性的基础上,以起重机起吊时刻和就位时刻的位形作为输入数据,规划出一条符合任务需求的路径作为输出数据。

起重机模型在该案例上某次的无碰撞规划结果如图9所示。

图9 FMT-based吊装路径规划结果

该案例在给定了起吊和就位位形之后,可以成功规划出一条较为平滑的路径。起重机在场区中一个障碍物环绕的起吊位置出发,其成功避开了车身两边的障碍物,并通过位于两个障碍物墙壁之间的缺口,运动到位于障碍物墙壁外围的就位位置。其中,位于起吊位形A和就位位形B之间的多个起重机,就是规划出的吊装动作序列中,各个时刻起重机所对应的位形状态,吊装动作序列两端显示的是吊装系统的起吊状态和就位状态。

2.2 吊钩位姿已知的路径规划

上述研究是针对起重机起吊位形和终止位形均已知的情况,然而在实际吊装过程中,知道的仅是被吊物的起始和终止的位姿,并不清楚起重机的整体位形。为此,笔者在给定了吊钩位姿的情况下,通过公式推导确定出起重机的位形,然后调用传统的运动规划算法FMT进行求解,寻找可行路径。

2.2.1 下车固定

由于下车固定,则其位置P(xc,yc)和方位角α均作为已知条件;同时,给出了吊钩的位姿,即给出了Xh、Yh、Zh和θh的值。

笔者将履带起重机的位形q=(x,z,α,β,γ,h,ω)分解为两部分(qm,qu),其中,qm=(x,z,α)为履带起重机下车的3个关节,qu=(β,γ,h,ω)则对应上车部分转台、臂架变幅、起升绳收放、吊钩旋转等4个自由度。

根据公式(3),可以依次求得β、γ、h、ω的值。至此,由吊钩位姿即可求出相应的起重机位形,进而调用传统的路径规划算法进行路径规划。

IK-based被吊物位姿给定的吊装路径规划(下车固定)的伪代码,如表2所示。

表2 IK-based被吊物位姿给定的吊装路径规划

在吊钩位姿已知,并且下车固定情况下,为了验证路径规划的可行性,笔者同样构建一个案例以证明模型的正确性,如图10所示。

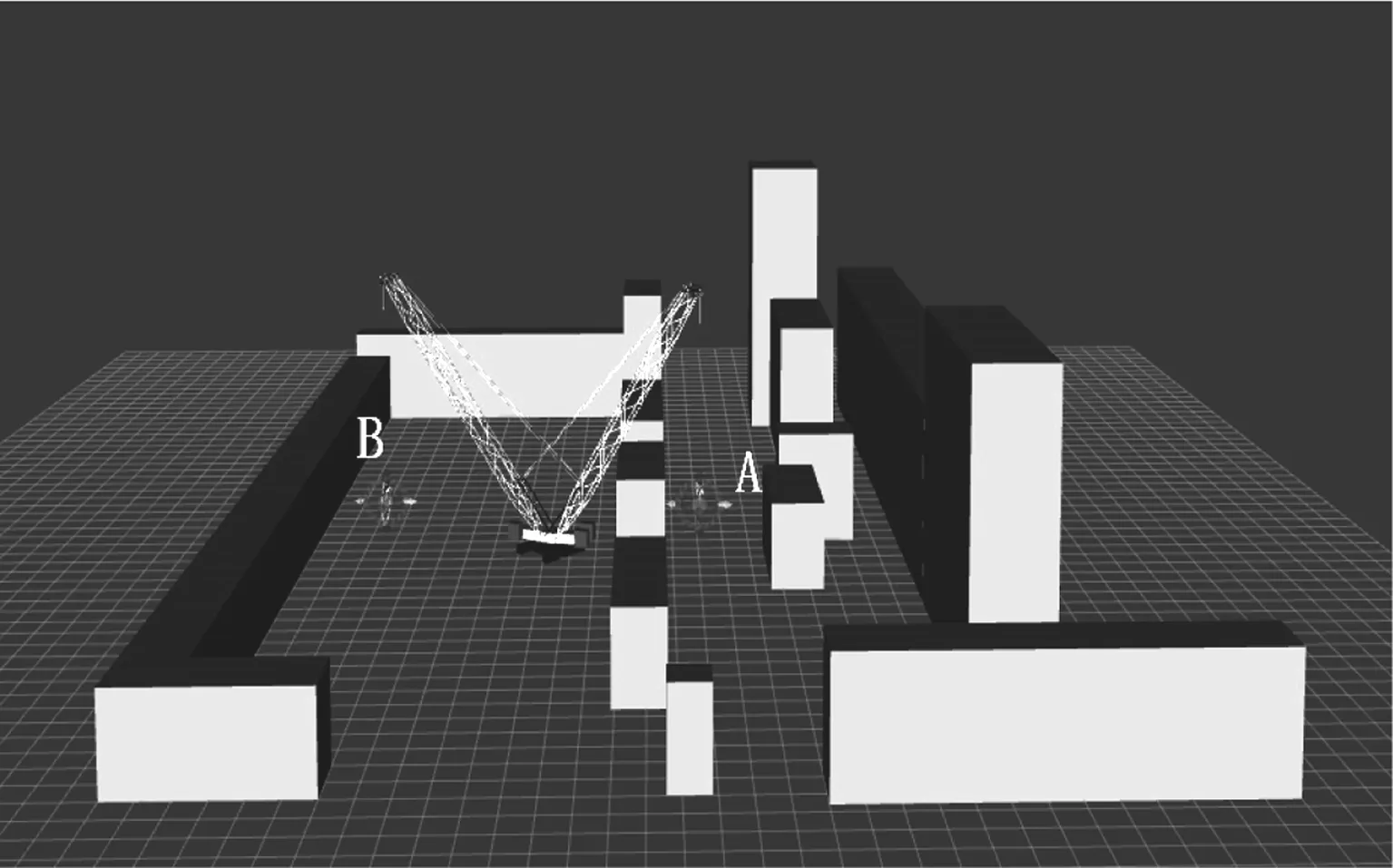
图10 IK-based被吊物位姿给定的吊装路径规划环境搭建(下车固定)

图10中,A为起吊时刻起重机吊钩位置,B为就位时刻起重机吊钩位置,要求起重机在保持下车不动的情况下,仅通过上车部分,即在四维空间中,根据起吊时刻吊钩位姿和就位时刻吊钩位姿,规划出一条能安全地将被吊物从A搬运到B的吊装动作路径。

该案例以起重机起吊时刻吊钩位姿和就位时刻吊钩位姿作为输入数据。首先,根据逆向运动学相关公式求解当前吊钩位姿下起重机的位形,在完成起重机起吊位形和就位位形的计算之后,规划出一条符合任务需求的路径作为输出数据。

起重机模型在该案例上某次的无碰撞规划结果,如图11所示。

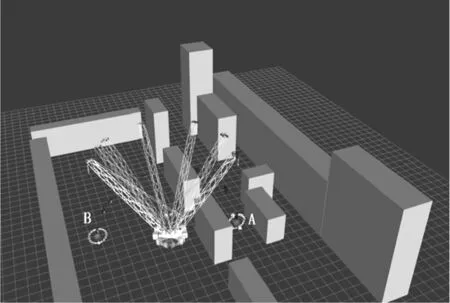
图11 IK-based被吊物位姿给定的吊装路径规划结果

该案例是在下车固定的前提下进行,即起重机在四维空间中进行规划,可以看到起重机成功避开了位于起吊时刻吊钩后方的障碍,在下车固定的状态下,将被吊物从场区中较为狭窄的两个障碍物墙壁之间的位置,用上车部分移动到较为宽广的区域。

其中,位于起吊位形A和就位位形B之间的多个起重机就是规划出的吊装动作序列中,各个时刻起重机所对应的位形状态,吊装动作序列两端显示的是吊装系统的起吊时刻吊钩状态和就位时刻吊钩状态。

2.2.2 下车不固定

当起重机下车不固定,并且仅给出吊钩的起吊、就位位姿,根据上述所提站位环可知,起重机会有多种位置取值,就会存在多解的情况。这里笔者将吊钩位姿p对应的起重机位形空间用集合C表示,即:

Csm={q|q=G(qm,p)|}

(13)

式中:G—履带起重机上车的逆向运动学。

这就会造成一个问题,即求解得到起重机位形,可能无法在位形空间中找到一条无碰撞路径。为此,需要反复求解起重机位形并且再次调用规划算法,直到获得一条可行的吊装路径。

IK-based被吊物位姿给定的吊装路径规划的伪代码,如表3所示。

表3 IK-based被吊物位姿给定的吊装路径规划

续表

在吊钩位姿已知,下车可在站位环中移动的情况下,为了验证路径规划的可行性,笔者同样构建一个案例以证明模型的正确性,如图12所示。

图12 IK-based被吊物位姿给定的吊装路径规划环境

图12中,A为起吊时刻起重机吊钩位置,B为就位时刻起重机吊钩位置,要求起重机能够在障碍物环境中,根据起吊和就位时刻吊钩位姿,规划出一条能安全地将被吊物从A搬运到B的吊装动作路径。

起重机模型在该案例上某次的无碰撞规划结果,如图13所示。

图13 IK-based被吊物位姿给定的吊装路径规划结果

该案例是在下车不固定,即在七维空间中进行路径规划,起重机需要从场区中一个位于障碍物环境外的起吊位置出发,然后,通过位于障碍物墙壁之间的狭窄过道到达就位位置。

其中,位于起吊位形A和就位位形B之间的多个起重机,就是规划出的吊装动作序列中,各个时刻起重机所对应的位形状态,吊装动作序列两端显示的是起重机起吊时刻状态和就位时刻状态。

3 结束语

针对履带起重机吊装路径规划过程中存在的建模、规划问题,笔者对柔性起升绳进行了分析,建立了面向吊装路径规划的履带起重机的模型。

笔者采用一个约束转动关节、一个虚拟连杆和一个移动关节等效起升绳,使履带起重机模型具有吊装过程中始终竖直并可变长的特性;在此基础上给出其正向运动学和一种伪解析的逆向运动学求解方法,使得能快速根据吊钩位姿求得起重机吊装状态;建立了吊装路径规划模型,给出了距离度量定义、路径长度定义、状态转移方程等基于随机采样路径规划方法所需的几个基本操作;最后,用仿真实验验证了履带起重机模型和路径规划数学模型的有效性。

研究结果表明:

(1)采用虚拟连杆抽象表达履带起重机的起升绳部件,符合起升绳的运动特性;虚拟连杆的水平轴转动关节与臂架变幅关节形成一种几何约束,令其成为一个被动关节,可时刻保持起升绳的竖直效果,稳定性较好;

(2)在仿真环境下,履带起重机的3组不同作业任务均可顺利完成,可以满足起重机吊装路径规划任务的工作要求。

笔者在建立履带起重机模型的时候,并未考虑基本动作的驱动方式,因此,得到的路径还需要做进一步处理,将其转化为驱动空间的输入量,才能控制驱动器,使起重机沿着所得路径运动。

在下一步的工作中,笔者将研究在驱动空间的建模,并把驱动方式融入到路径规划过程中。