均值-标准差质控图在检测实验室质量控制中的应用

谢静，於迪，丘晖饶，张琳颖，王永安，朱懋冠，黄文娟

（广州机械科学研究院有限公司，广州 510530）

实验室的质量控制体系文件中规定实验室需有质控程序与质控规划，以监控测试与校准结果的实效性。在质控数据超过预先确定的质量评估依据时，需使用有规划的措施来改善存在的质量问题，从而确保数据的准确性。质量控制不仅可有效保证实验室检测结果的公正性、准确性和可靠性，还可反映实验室的检测能力，促进实验室提高对检测质量控制的认识和结果评价工作[1-2]。

质控图是监视和分析检测数据质量的有效措施之一，也是实验室内部质量控制的一个重要手段[3]。1924 年，美国休哈特[4]首次用质控图实现了工艺管理，不但可以直接管理生产过程，还能保证生产质量，从而达到以预防问题为主的目的。

目前国内外针对均值-标准差质控图的应用及其影响因素的研究较少。在日常工作中，实验室的检测结果易受不确定因素的影响，从而产生偏离，若不能及时发现，可能会导致检测结果失效，造成严重影响。如何利用均值-标准差质控图对检测结果进行有效地监控，以及如何排除影响质控图的因素，均是实验室需要解决的关键问题，笔者对此进行了初步探索。

1 质控图原理

质控图是假设测试分析在可控制状态时，总体分析结果的质量特性是正态分布N（µs2），它的图形是来自于正态分布的曲线图。按照质控图的理论，正态分布概率见表1。

表1 正态分布概率分布表

由正态分布性质以及小概率原理[5]可知，当一个质量指标值与真实值的偏差：

(1)在±3 s内， 若只有正态的偶然变差，为“控制中”的值；如果在控制线之外，出现超过正态或偶然变差的因素，称之为“限制外”的值。

(2)在±3 s外，出现的概率为0.27%。

(3)测量值在µ-3 s与µ+3 s之间，概率为0.1%。

因此在质控图中，测定数值超出µ±3 s 范围是小概率事件，一旦出现，测定数值就会被判为异常。

±3 s 原理确定的质控图控制界限，被视为是最经济合理方式，一般使用此方式，按照统计原理来绘制常规质控图[6]。

2 质控图的绘制

2.1 数据的收集

选择在日常检测中积累了数据的样品，确定测量系统处于稳定或统计控制状态，将该样品进行至少20次重复测定，且每次测定的结果均满足规定的精密度和准确度，以确保数据对绘制出来的控制图的判断过程处于稳定状态。

2.2 统计量形式的确定

对样品中测试20个以上的数据展开分析，并按以下公式算出平均数、标准偏差s、平均极差等来确定控制图的统计量形式。

（1）总均值：Xˉ =（X1-X2）/2，X˭ = ∑Xˉ/n，X1和X2均为平行分析样品的测定值。

2.3 控制限的计算

根据GB/T 17989.2—2020《控制图 第2 部分：常规控制图》［7］表1“计量控制图控制限的计算公式”求得控制上限值UCL和控制下限值LCL，式中A2，A3，B3，B4，D3，D4是控制图系数，可由控制图系数表查得，计量控制图控制限的计算公式如表2所示。

表2 计量控制图控制限的计算公式

2.4 绘制控制图

以测定序号为横坐标，以质量特性值为纵坐标，中心线、±2 s 上下警戒限、±3 s 上下控制限，分别绘点制作控制图，结构如图1所示。

图1 质控图结构

通过数据节点是否处于上、下控制线之间以及数据节点的排列状况，来评估检测过程的控制状态[8]。测定结果的预期值为中心线；±3 s 为控制限域，限内表示可接受域；±2 s 超过此区域,即应受到注意的警告限域；±1 s 是核查检测数据质量的辅助指标域。

2.5 质控图状态的判定

质控图的判稳准则：（1）点全部在界限内；（2）界限内的点无排列缺陷。

质控图的判异准则：（1）点出界；（2）界内点排列不随机。

判异标准：GB/T 17989.2—2020《控制图 第2部分：常规控制图》附录A［7］，其中提到了8种典型的波动异常图形（1 个点落在A 区以外、连续9 点落在中心线同一侧、连续6点递增或递减、连续14点中相邻点交替上下、连续3点中有2点落在中心线同一侧的C区以外、连续5点中有4点落在中心线同一侧的C区以外、连续15点落在中心线两侧的C区内、连续8 点落在中心线两侧且无一在C 区内），分别如图2（a）～（h）所示。

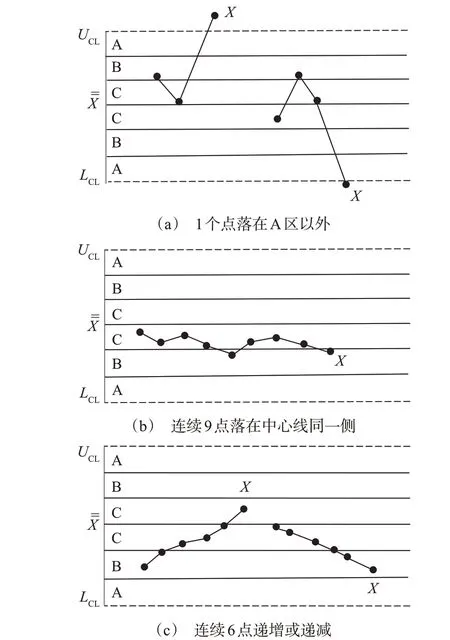
图2 8种异常质控图

质控图用于检测过程质量控制效果，在进行试样测定之前，可以先对质控样品进行测定，在计算质控样品测定结果的平均值、极差以及标准偏差后，再在控制图上画点，可以直观地反映实验室分析工作的质量[7-12]。

(1)若测量值位于中心线附近及上警告线或者下警告线的范围内，则表明检测过程受控，分析数据可信；

(2)若测量值超过上、下警告线范围，但在上、下控制界限之间的范围内，则表明分析质量较差，检测过程可能出现失控情况，需对检测过程做初步核查，并采取相应的处理措施；

(3)若测量值落于上、下的控制线以外，即表明测定过程不受控，检测数据不能采用，应立即核查检测过程，找出失控因素，并加以修正[7]。

3 质控图实际应用

以某水泥公司送检的齿轮油作为控制样品，按GB/T 7304方法测定酸值含量，检测设备为“奥秘一代酸值测定仪”，不同人测定的同一个样本中，共采集25 个子组，子组数量为5。每个子组为一个人员的测量值，分析数据见表2。以测定序号为横坐标，以平均测量值为纵坐标，描绘均值-标准差质控图。

表2 控制样测试数据

3.1 绘制标准差计量控制图

中 心 线CL=sˉ = 0.021；上 控 制 限UCL=B4sˉ =0.0439（B4=2.089）；下控制限LCL=B3sˉ = 0(B3= 0)。系数B3、B4均根据GB/T 17989.2—2020中“计量控制图控制限的因子”表查得，绘制的标准差质控图如图3所示。

图3 标准差质控图

3.2 绘制均值计量控制图

中心线CL=X˭=0.697；上控制限UCL=X˭ +A3sˉ =0.727（A3=1.427）；下控制限LCL=X˭－A3sˉ = 0.667。系数A3根据GB/T 17989.2—2020 中“计量控制图控制限的因子”表查得，绘制的均值质控图如图4所示。

图4 均值质控图

依据控制图的判稳原则与判异原则，图3和图4满足判稳原则,为连续25 个点，边界外点数为0；同时不属于8种判异质控图中的任意一种。此质控图表明测量系统处于统计的受控状态。

3.3 控制图检测过程监控

由图3和图4可以看出，两图联合可以监控检测过程是否受控，从而保证检测结果的准确度和精密度。通过质控图可以监控和评估实验室是否具有可靠的检测能力，数据点位于上限值以上位置或下限值以下位置，都表明该结果在质控图中呈现异常状况；超出上、下控制限，说明测定过程失去控制，分析结果不可采用，需及时查找原因并进行纠正，然后再重新测定前后批次的样品，确保数据的可靠性。

4 质控图的影响因素

质控图是由检测数据点绘制而成的，而检测数据的准确性易受到各方面因素的影响。检测数据的异常不但会影响质控图的判定，还会影响实验室检测活动能否顺利进行，应针对检测活动相关人、机、料、法、环等因素逐项分析，找出检测结果异常的原因并进行纠正[13-16]。

5 结论

（1）依据质控图的控制限及时发现数据的异常趋势，可以对实验室能力起到有效的监控，以及直观分析和评估是由偶然因素或者系统原因所引起的质量波动，以便指导操作者做出正确判定，必要时及时采取处理措施。

（2）质控图的类型有很多，子组样本量大于10以上的，利用电子设备来计算过程的控制限时，均值-标准差控制图不但能准确的监控实验室能力，还能提高工作效率。

（3）确保质控图的可控制状态，必须保证数据的可靠性，即为实验室检测活动中人员培训、仪器核查校准、方法标准学习、环境条件监控等提供参考依据。

（4）质控过程需要有重复性这样的统计规律，一次性或少数几次的过程目前不好应用在控制图进行控制。