复习课中突出本质、优化通法的教学思考*
蒋亚军
⦿浙江省宁波市第四中学
复习课是查漏补缺、完善技能、落实素养的基本课型,而一题多解、一题多变是常见的一种模式.传统复习课以教师讲学生听为主,学生的探究学习体验少,没有体现学生的主体地位,忽视了学生活动经验的积累.本文中通过一节关于椭圆中两直线斜率和(积)为定值与直线过定点的复习课,探究一题多解优化运算凸显问题本质,实现一题多变,多角度理解数学对象形成通法,引发对“一题一课、多解变式”复习课的教学思考.
1 题目呈现及前期准备
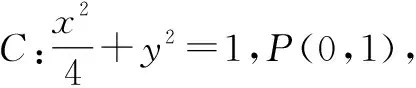
这是一道椭圆中的定点定值问题,题目难度适中,适合学生自主完成解答.考虑到课堂重心在于学生理解问题的本质,形成优化后的通性通法,将问题以作业的形式前置,便于了解学生的解答情况.
2 教学环节
2.1 一题多解凸显本质

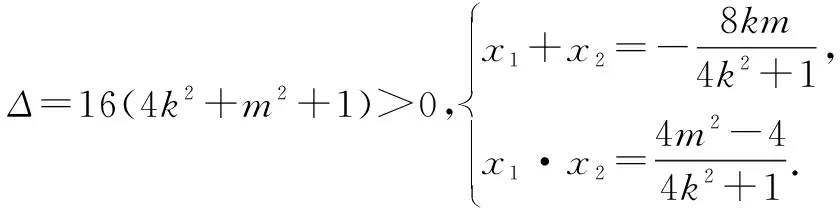
师:本题的已知条件和目标要求是如何联系起来的呢?
生1:先将PA,PB的斜率表示出来,再利用斜率和等于-1即可.当然最主要的还是在计算上不要出错.
生2:思路和方法我都会,就是计算的时候经常会出错,特别是在对斜率之和通分与代入化简的过程中,稍不留神就会出错.有没有一种能减少计算量的解法呢?
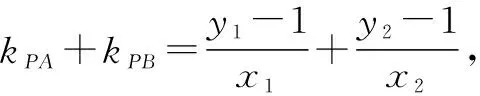
生3:kPA和kPB的结构是一样的,要出现含有y-1和x的式子,只需对椭圆和直线分别进行转化就可以了.
师:很好!你能对椭圆方程进行转化吗?
师:现在已经将椭圆和直线方程都转化为含有x和y-1的式子,接下来怎么办呢?联立方程,消元,利用韦达定理?
生4:这样不是与前面的解法一样了吗?计算量没有减少.
生5:椭圆方程两边同时除以x2!
生6:不行的,次数不统一,又不是齐次式.
师:那该怎么办呢?

生7:我还有新的想法,因为直线方程是自己构建的,所以把直线方程设为mx+n(y-1)=1,就不会出现分母m-1了.
师:同学们都很棒,从减少计算量这一目标出发,不断修正解题过程,最后圆满完成设定目标.数学解题就是一个不断深入本质、优化方法的过程,让我们一起整理一下优化后的解法——“齐次化”法.

点评:将学生的解法投屏,展示其思维过程,对题目的已知和所求进行分析,联系已有知识对所求目标进行转化和化归,架起解决问题的桥梁.学生出现了对斜率是否存在未讨论,或在联立直线和椭圆方程消元得到韦达定理时计算出错,或在代入斜率公式计算时出错等问题.通过对比,说明学生的运算求解能力需要加强.通过学生暴露出来的计算问题,以减少计算量提高准确率为目的,引导学生发现斜率之和(积)为定值这类问题的本质,构造关于目标斜率的齐二次方程,利用韦达定理进行转化和求解.这样就能使问题较快地得到解决,形成优化解法.
2.2 一题多变注重通法
师:用“齐次化”的方法可以有效减少计算量,但需注意的是要配成齐二次的形式.如果把条件kPA+kPB=-1换成kPA·kPB=-1,你能否很快解决吗?
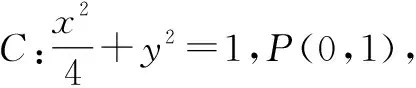
师:很好!“齐次化”的本质就是构建关于斜率的韦达定理.如果改变条件和结论的顺序,你能证明吗?
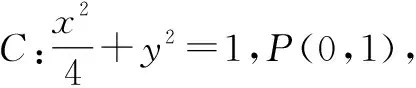
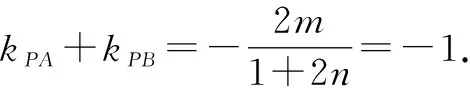
师:将点P从椭圆上移到椭圆外,得到变式3,你能求出定点吗?对更一般情况的变式4,你还能证明吗?抛物线和双曲线中还能用这种方法吗?
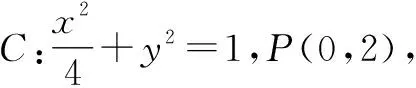
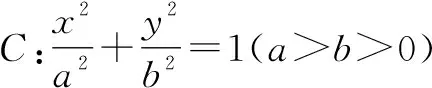
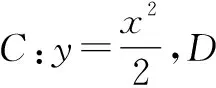
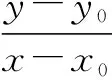
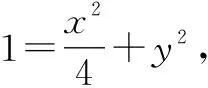
3 教学反思
3.1 基于学情选择合适的例题
复习课的定位应该是“基础知识的掌握、基本技能的提高、基本思想方法的落实、基本活动经验的积累”.因此,例题的选择要根据教学目标着眼于学生的最近发展区,“跳一跳,能摘到”,为学生提供适合的内容,调动学生积极性,发挥其潜能[2].解析几何中的定点定值问题是考试的热点,学生往往有思路、会方法,但由于计算问题不能顺利解出答案.针对这一现象,从一道高考改编题入手,通过师生互动启发,生生互动完善,挖掘定点与定值问题的本质,构造目标斜率的齐二次方程,在学生原有的解法上进行优化,总结形成解决这类问题的通性通法——“齐次化”.
3.2 基于学情进行合理变式
变式教学的目的就是突出数学本质、提炼解题方法,实现解一题通一类、解一类用一法的效果,使知识网络化、方法程序化.通过改变条件、结论、顺序等,有意识地引导学生思考变式怎么变、为什么这么变、还可以怎么变,激发学生的学习兴趣.围绕着“齐次化”这一通性通法,将定点定值问题深层次的本质挖掘出来.任何解决数学问题的方法背后都是有思考过程的,而理解又是思考的基础,因此对问题本源的思考与分析在课堂教学中是非常重要的[3].
4 结束语
圆锥曲线中的定点定值问题,是高考和模考的热点问题,学生往往有思路而解不出最终答案,因此得分率不高.直接运算是数学运算的低级水平,往往伴随着大量繁杂的计算;合理运算是数学运算的中级水平,利用转化化归的思想,减少计算量达到求简的目的;创新运算是数学运算的高级水平,既快又准地得到答案,追求至简的目标.通性通法重要,是学生必须掌握的方法和技能,在此基础上通过合理转化,往往会减少计算量.

