高中数学解题过程中学科核心素养培养探索
汤艳丽
⦿江苏省如皋中学
新时代素质教育改革提出中小学教育要以培养学生学科素养为教育教学价值导向,通过多元化学科课堂教学途径培养学生科学的学科学习思维、正确的人生价值观念以及高质量的自主学习能力.基于此,在高中数学教育教学过程中教师要充分利用数学学科核心素养,以培养学生综合学科素养为教学价值导向,进而全面提升学生综合素质.
数学学科核心素养是学生数学学习思维、方法、能力的统称,也是历年来高考命题考查的热点.培养与提升学生数学学科核心素养,就是要在数学教学以及学生进行数学解题训练过程中,注重培养与锻炼学生快速处理数值计算与分析能力、几何空间图形及其位置关系想象能力、数形结合与抽象具象转化能力以及逻辑联想与推导能力.据此,笔者以高中数学经典例题解析为参考,探究数学解题过程与学科核心素养价值导向间的相互融合.
1 数值计算与分析能力的培养
大量的数值计算以及通过数据对某一数学现象进行深入分析是高中数学学习的一大难关.在教学过程中教师不能够盲目夸大题海战术带来的数学计算能力培养的效果,否则不仅会加重学生数学学科的学习负担,且会让数学课堂变得枯燥,失去数学学科的教学意义.教师应该合理安排数值计算与分析题目的练习计划,通过精准、典型的数学例题,引导学生进行数学思考,帮助学生学会从数值中发现联系进而进行数值计算、数值建模、数值分析和后续的模型推导与总结.
例1某企业对三个工作车间的人数进行统计,其结果如表1所示.用分层抽样的方法分别从三个车间抽取30人,其中三车间有12人.
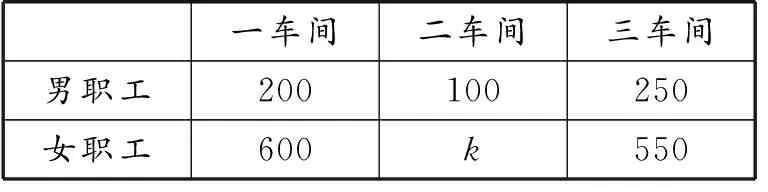
表1 三个车间人数统计 单位:人
(1)求第二车间女职工人数(k值);
(2)为了统计企业职工请休假情况,对一车间男职工进行001—200编号,用系统抽样的方法从中抽取5人,其全年请休假天数分别为75,79,82,73,81,且请休假73天的职员对应编号是145,问请休假75天的对应职员编号是多少?求所抽取5个职员请休假天数的方差.
分析:本题主要考查数据统计中分层抽样、系统抽样方法以及标准差、方差、极差的概念与计算.要求学生观察与理解表格数据信息并准确地进行数值计算与分析,对学生数据识别与处理能力要求较高.
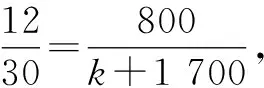
(2)由题意可知,系统抽样过程中的抽取间距为
设请休假75天的对应职员编号是m,则由145=m+(4-1)×40,解得m=25.
所以请休假75天的对应职员编号是25.
由题设已知条件,可求得
因此,所抽取5个职员请休假天数的方差为
2 几何空间图形及其位置关系想象能力的培养
高中数学学习中,空间几何图形的性质及动态变化图形之间位置关系是一大难点.解决此类问题需要学生具有良好的数学抽象思维、建模能力以及空间想象能力、几何判断能力.在教学中,教师要注重几何基础知识的讲解以及对学生空间想象思维的培养,通过解题训练锻炼学生想象能力,帮助学生学会从已知数学条件中发现问题并以扎实的数学基础探索解决问题的有效方法.
例2如图1,在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,且AC与BD相交于点O,点E是线段BP的中点,满足AP=CP,BP=DP.
(1)证明:AB⊥OP;
(2)设OP=2,求三棱锥A-BCE的体积.
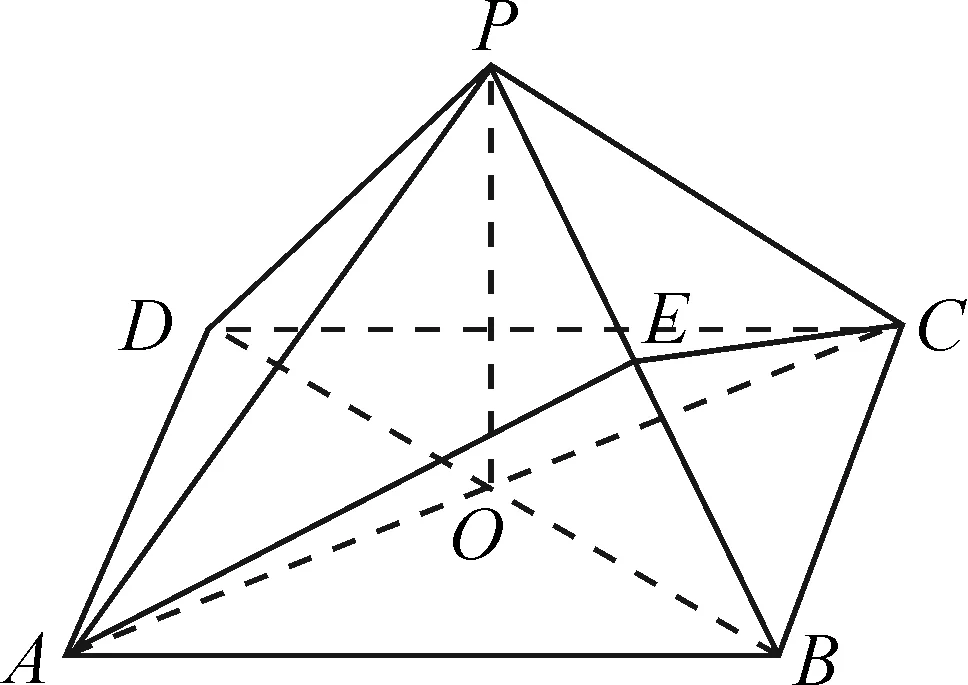
图1
分析:本题主要考查空间图形的判断及相应体积求解公式、空间中两直线的位置关系.要求学生具有一定的空间想象能力、逻辑推导能力并熟练掌握常见几何体的面积、体积公式.
解析:(1)因为棱椎的底面ABCD是正方形,且点O是AC与BD的交点,所以点O为AC,BD的中点.
又因为AP=CP,BP=DP,所以AC⊥OP,BD⊥OP.
因为AC∩BD=O,AC,BD均在平面ABCD内,所以OP⊥平面ABCD.
故AB⊥OP.
(2)由题设条件,易知

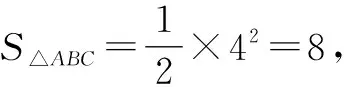
3 数形结合与抽象具象转化能力的培养
“几何直观”是新课程素质教育教学大纲所提出的高中数学关于培养学生数学思维的核心概念之一.因此,在教学中高中数学教师要注重对学生数形结合思维的培养.在相关题目解答过程中,教师要引导学生学会通过对事物的直接感知,发现数学问题背后事物的本质联系,依据想象构建清晰的数学图形并建立明确的数形联系,利用数形转换解决数学问题.
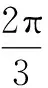
(1)求母线l的长度;
(2)求此圆锥的体积.
分析:此题主要考查几何图形间的位置关系、圆锥侧面展开图及其面积公式、圆锥体积公式等.要求学生将题中抽象的数学语言转换为直观的数学图形,从数形结合的角度找到解题关键点.
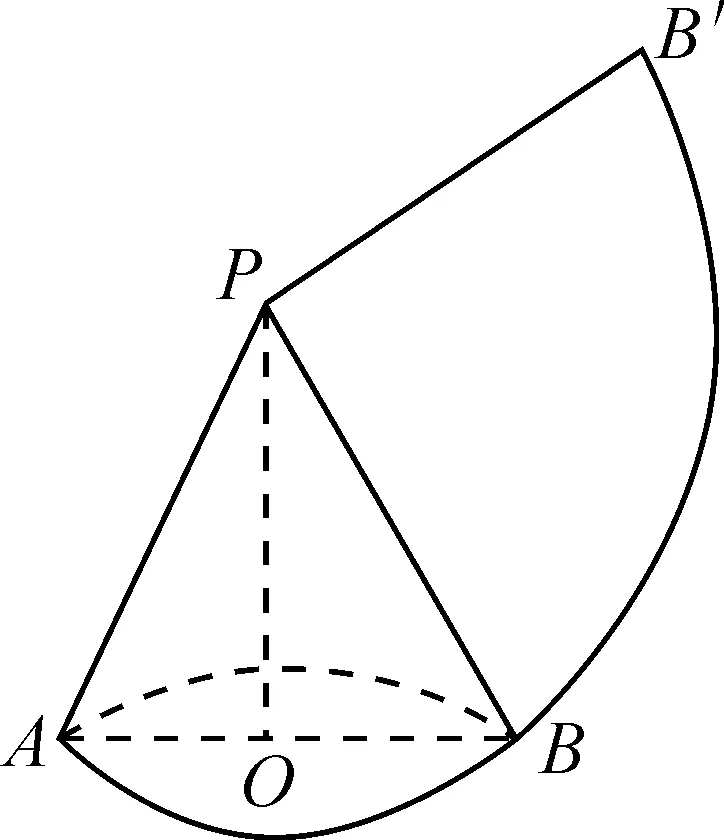
图2
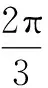
由2πr=2π,得r=1.所以圆锥的体积为
4 逻辑联想与推导能力的培养
逻辑联想与推导能力要求学生从现有的数学理论认知和相关数学命题出发,从一个问题切入点联想丰富的数学理论知识,以全面的数学视角分析问题并推断涵盖面更为广泛的数学命题.在高中数学解题中考查学生逻辑联想与推导能力主要体现在寻找数学规律上,如数列中的杨辉三角等数学问题.教师要充分理解此类数学问题的本质规律,在解题过程中训练学生逻辑思维.

(1)判断集合B={-1,0,1}是否为“闭集”,并说明理由;
(2)假设集合A是闭集,证明:若x,y∈A,则有x+y∈A;
(3)假设集合A是一个“闭集”,判断命题“若x∈A,则有x2∈A”的真假,并说明理由.
分析:此类题目是高中数学关于集合的概念与性质内容考查常见的出题方式,在学生已有的关于集合理论知识的基础上提出一个新的定义,要求学生在对集合概念与性质理解的基础上,利用逻辑推理对另外的数学命题加以判断,以找到命题之间的本质联系,理解其中的数学含义.
解析:(1)因为-1-1=-2∉B,所以由“闭集”定义可判断集合B={-1,0,1}不是闭集.
(2)证明:因为集合A是闭集,所以0∈A.若y∈A,则0-y=-y∈A.
所以由x∈A,可知x-(-y)=x+y∈A.
(3)因为x,y∈A,1∈A,所以x-1∈A.于是,当x≠0,且x≠1时,有
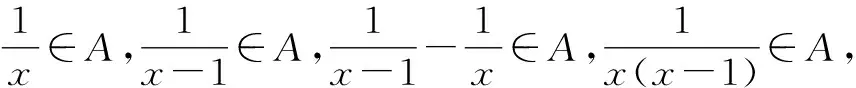
由(2)可知,x(x-1)+x∈A,即x2∈A.
故命题“若x∈A,则有x2∈A”是真命题.
通过数学经典例题的讲解以及学生对相关数学问题的解答与思考,能够帮助学生建立系统的数学思维模式,锻炼其发现并解答数学问题的能力.但教师要走出题海战术误区,从关注学生解题结果转向关注学生解题过程.教师要引导学生在解题过程中提高自身数值计算与分析能力、几何空间图形及其位置关系想象能力、数形结合与抽象具象转化能力以及逻辑联想与推导能力等,充分将数学学科核心素养与高中数学课堂教学过程相融合.教导学生解题时不能急于求成,而应反复斟酌与推敲,学会以不变应万变,帮助学生形成良好的数学解题习惯与思维模式,进而全面提升学生综合素质.这将对学生今后的学科学习大有裨益.

