追本溯源：2022年新高考Ⅱ卷第21题解法探究

李中勇 郭万里 秦 君

⦿四川外语学院重庆第二外国语学校

1 试题再现

(1)求C的方程；

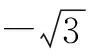
①M在AB上；②PQ∥AB；③|MA|=|MB|.

2 第(2)问解法分析

思路1：此题涉及直线PQ与双曲线相交，因此可以利用解析几何常规处理方法，先从设直线着手.设出直线PQ的方程，与双曲线方程联立，由韦达定理得出x1+x2，x1x2.以P，Q的坐标为载体，根据直线PM，QM的斜率，可以利用直线方程的点斜式写出PM，QM直线方程，联立得出点M的坐标，进而得出点M的轨迹方程.同时，可以用点差法研究AB中点N的轨迹.对照二者的轨迹方程，可以任意选择①③⟹②或①②⟹③或②③⟹①.

思路2：从条件入手，不同的条件对应不同的解法思路.

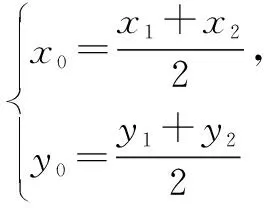
(2)参考新人教A版选择性必修第一册(2020年5月第1版)第128页习题3.2拓广探索第13题,根据直线PQ与双曲线相交，并结合|MA|=|MB|，可以联想到中点弦问题.

(3)参考新人教A版选择性必修第一册(2020年5月第1版)第68页探究与发现，根据①M在AB上，及③|MA|=|MB|，可以联想到利用直线参数方程中t的几何意义和倾斜角α来解决问题.

解法思维导图如图1所示.

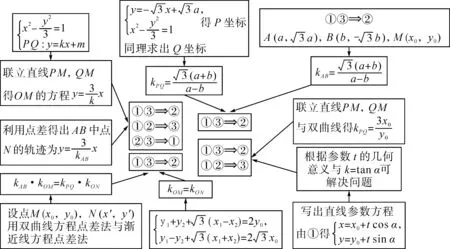
图1

3 具体解法

解法1：轨迹探索.

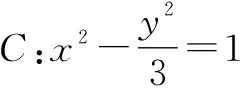
(3-k2)x2-2kmx-m2-3=0.

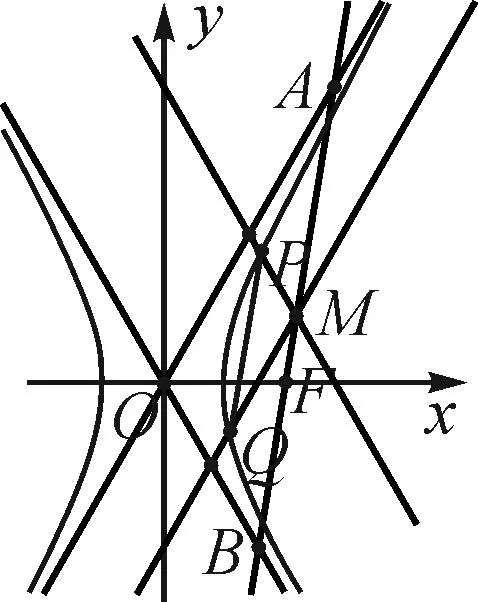
图2

设点M的坐标为(xM,yM)，则

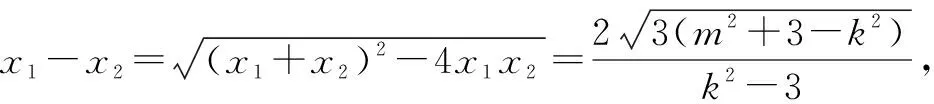
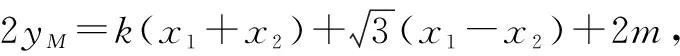
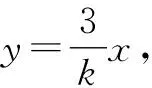
设A(x3,y3)，B(x4,y4)，AB中点为N(x0,y0).

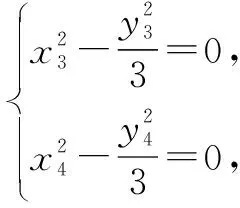
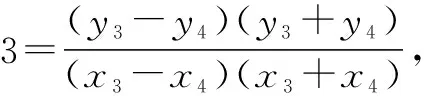
若选择①②⟹③.

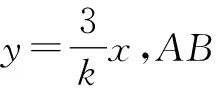
若选择①③⟹②.

若点M,N重合，则k=kAB，所以PQ∥AB.

若选择②③⟹①.

因为PQ∥AB，k=kAB，则M，N重合，所以M在AB上.

解法2：选择①③⟹②，通过寻找点之间的关系，利用中点和斜率坐标表示.

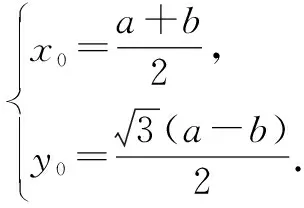
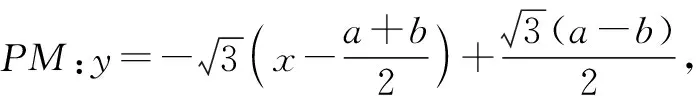
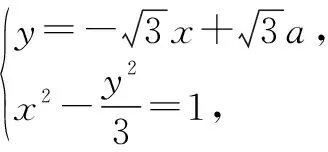
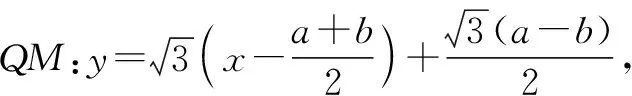
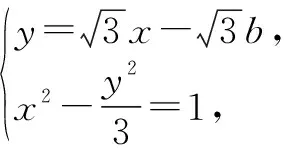
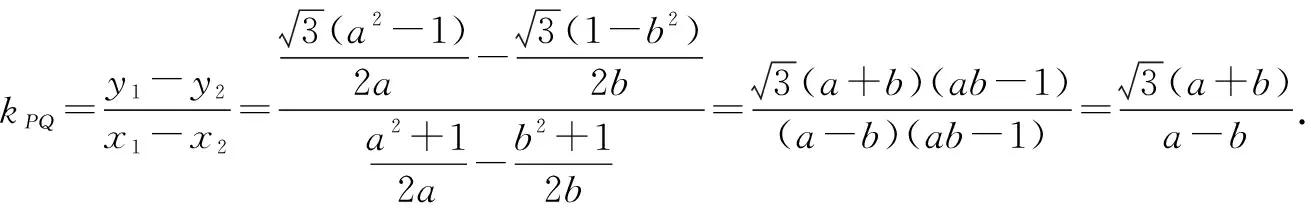
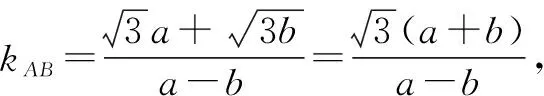
解法3：选择①③⟹②，双曲线的点差法与退化双曲线(渐近线)的点差法相结合.

由题意，可设P(x1,y1),Q(x2,y2)，M(x0,y0),N为PQ的中点.

前面已经由点差法得到kAB·kOM=3.

同理可得kPQ·kON=3.

即kAB·kOM=kPQ·kON

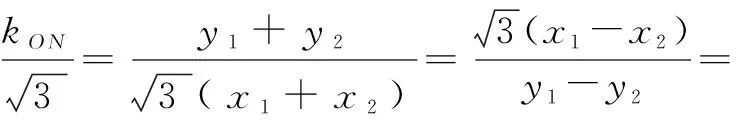
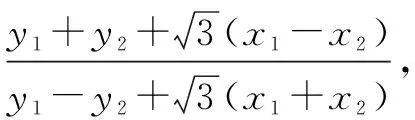
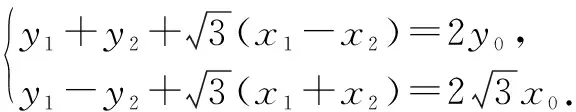
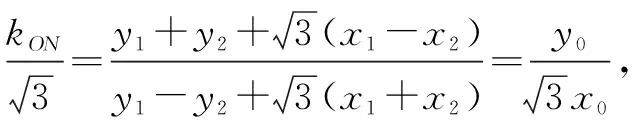
综上可得kAB=kPQ，即PQ∥AB.

解法4：设M(x0,y0)，则直线PM的方程为

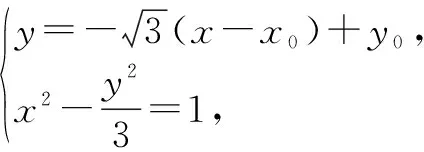
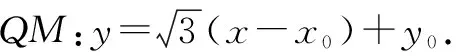
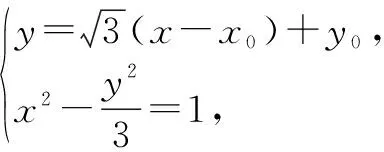
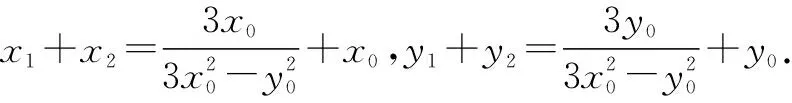
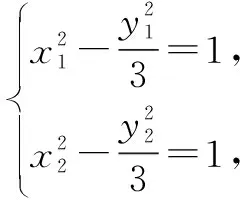
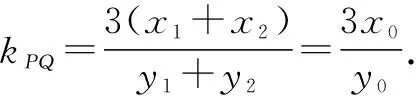
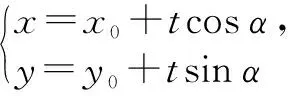
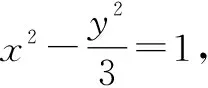
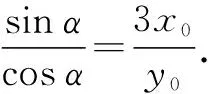
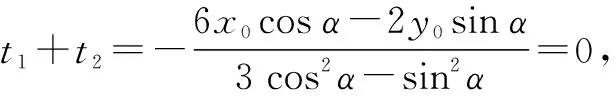
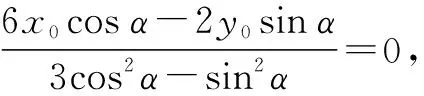
即kAB=kPQ，所以PQ∥AB.

4 思考与延伸

思考：在上述试题解法中，并没有用到直线AB过双曲线的右焦点F这一条件，因此直线AB不经过双曲线的焦点F，本题的结论依然成立.

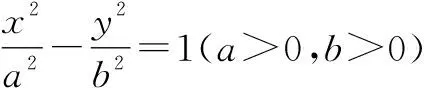
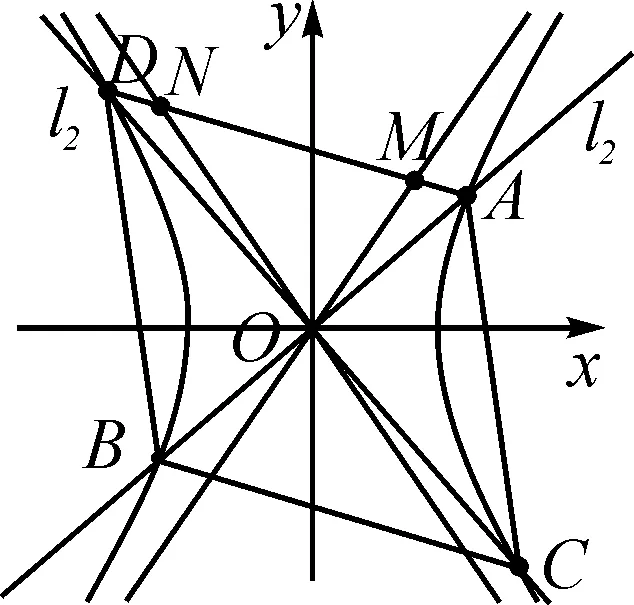
图3

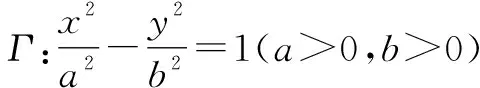
(1)求Γ的方程；

(2)如图3，过原点O作相互垂直的直线l1,l2分别交双曲线于A，B两点和C，D两点,A，D在x轴同侧.设直线AD与渐近线分别交于M，N两点，是否存在直线AD使M，N为线段AD的三等分点？若存在，求出直线AD的方程；若不存在，请说明理由.