两栖仿生机器人登陆自适应越障机构优化设计*

殷 谦，王 何，宋 震，尚建忠，罗自荣

(1. 长沙理工大学 能源与动力工程学院, 湖南 长沙 410114; 2. 国防科技大学 智能科学学院, 湖南 长沙 410073)

水陆两栖仿生机器人可在陆地、近海滩涂及其他两栖环境中工作[1]，在安全救灾、资源开发、环境勘探等领域具有广阔前景[2]。在两栖机器人工作中，机器人登陆需要克服沙滩、岩石等复杂地形环境，对其越障能力提出很高的要求。

根据仿生模本不同，水陆两栖仿生机器人主要包括鳍片多足结构[3]、仿青蛙或蝾螈结构[4-6]、仿海龟结构[7-8]、仿蛇形结构[9-10]、仿蟑螂结构[11-13]等类型，这些机器人通过模仿某一种两栖生物来实现运动，两栖环境适应程度有限，尤其是在浅滩登陆过程中，攀越复杂障碍能力不足。为提高机器人的登陆越障能力，一些学者采用水下和陆地两套驱动系统集成的方法。德国学者提出了仿蛇机器人Kairo[14]，其采用轮式驱动与多关节来实现陆地行进与水下巡游动作；文献[15]研发的仿蝾螈机器人在水下依靠紧贴身体的关节波动推进，陆地行走通过蜿蜒躯体实现。

一些针对陆地或水下机器人推进机构的研究，为两栖机器人的设计提供参考。一方面，陆地机器人采用轮和履带来实现复杂地形越障，例如：饶伟等[16]设计了一种关节履带机器人，其能够对台阶一点或多点接触实现越障动态稳定；Gong等[17]提出了一种轮履式越障平台并实现多机器人协同工作。另一方面，水下机器人采用波动鳍实现推进，例如：Curet等[18]通过PIV手段分析了波动鳍的三维流场和涡流；在此基础上，Hu[19-20]等对波动长鳍进行动力学建模，通过分析鳍面的水下运动性能优化其结构，实现水下推进效率大幅提高。

鉴于仿生波动鳍和轮分别在水下和陆地具有高效推进能力，本文将二者组合，设计一种轮鳍复合式水陆两栖仿生机器人，其兼具陆地与水下高效运动的优点。针对该机器人从水面至陆地的登陆过程，本文设计了独特的具有自适应攀爬功能的越障机构，优化设计机器人越障过程的结构与运行参数，通过仿真与实验验证了其自适应越障性能，较好解决了复杂两栖环境机器人登陆越障难题。

1 自适应攀爬越障轮机构的基本原理

轮鳍复合式水陆两栖机器人的原理结构如图1所示，由越障轮机构、波动鳍、螺旋桨、信号天线等部分组成。机器人水下运动由仿生波动鳍提供前进推力，车体前侧安装有两个螺旋桨，用于控制车体在水下的姿态。

图1 两栖机器人总体结构示意图Fig.1 Structure of the amphibious robot

机器人地面行走系统采用了独特设计的自适应攀爬越障轮机构，结构如图2所示，包括一套两级减速定轴轮系和一套两自由度行星轮系。定轴轮系由电机齿轮驱动，经一级齿轮和二级齿轮降低速度提升扭矩，驱动行星轮系的中心齿轮，以适应于桨叶轮翻转越障。行星轮系由越障行星摇臂、中心齿轮、传动齿轮和桨叶轮构成，中心齿轮带动两边的传动齿轮旋转，驱动桨叶轮的齿轮轴带动桨叶轮旋转。

图2 越障轮内部结构示意图Fig.2 Structure of the obstacle climbing wheel

机器人越障原理如图3所示：①在平路运动时，如图3(a)所示，越障行星摇臂不翻转，机器人的传动系统类似定轴轮系，电机驱动桨叶轮带动机器人水平前进；②当机器人桨叶轮碰到障碍时，如图3(b)所示，由于车轮受到堵转力矩，电机带动越障行星摇臂整体翻转，机器人整体前送；③当越障轮翻转后，桨叶轮搭上前方障碍并继续翻转，抬升躯体整体搭上台阶，如图3(c)所示；④当躯体前端高度超过了障碍后，越障轮继续翻滚并能同时向前运动，如图3(d)所示，使整个机器人跨越障碍。

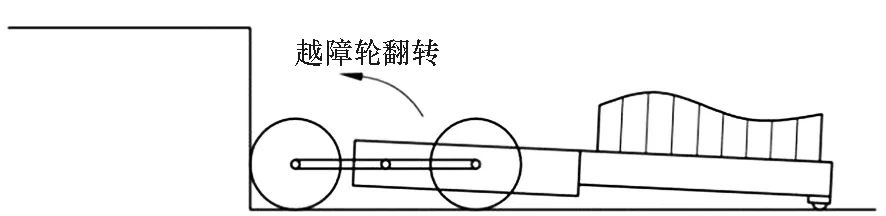
(a) 水平地直行(a) Go straight on the ground

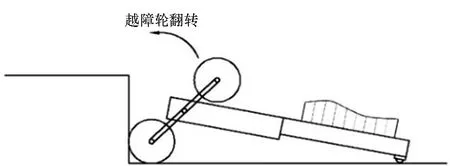
(b) 开始越障抬起后轮(b) Lift the climbing wheel

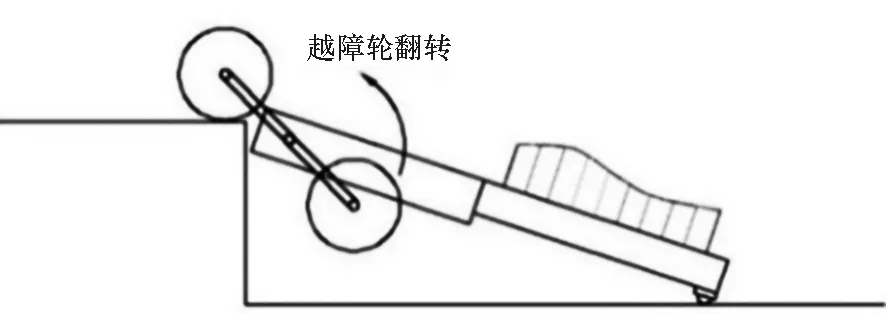
(c) 越障轮搭上台阶(c) Climbing wheel on the obstacle

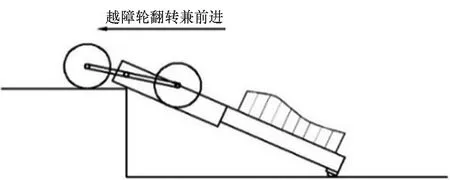
(d) 越过障碍(d) Obstacle climbing complete图3 机器人越障过程示意图Fig.3 Process of the obstacle climbing

2 攀爬越障轮机构的越障力学模型

建立机器人质心运动学与力学模型，如图4所示：固定坐标系x0O0y0，机器人坐标系x1O1y1，摇臂坐标系x2O2y2。后车体和行星摇臂质量分别为m1和m2，l1、R分别为摇臂中心至机器人车体尾端、越障轮摇臂的长度，Lc1为机器人车体质心与O1之间的距离，r为越障轮半径，α、β分别为机器人的俯仰角和前摇臂摆角。

图4 机器人在越障临界状态下的运动受力情况Fig.4 The force of the obstacle climbing in the critical state

前摇臂轮坐标系x2O2y2与机器人坐标系的变换矩阵可写为：

(1)

由上述分析可知，机器人质心在坐标系x1O1y1中的表达式为：

(2)

其中：m为机器人总质量；1p1和1p2分别为车体与前摇臂在坐标系x1O1y1中的坐标矩阵，可表示为

(3)

(4)

机器人在越障过程中，其质心坐标在固定坐标系x0O0y0中表示为：

(5)

其中，0T1为前摇臂在坐标系x1O1y1中与固定坐标系之间的变换矩阵，Px、Py和Pz为机器人坐标系x1O1y1在固定坐标系中的位置。

对机器人越障临界位置进行质点运动学分析，令机器人质心坐标为(Lx,Ly)，越障高度H为：

(6)

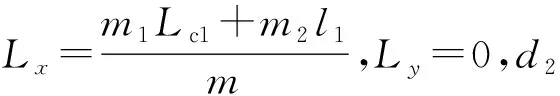
针对机器人越障临界状态进行力学分析，FN1、FN2和N2分别为地面、障碍台阶和障碍边缘对机器人的支撑力，F2为桨叶轮在台阶上转动产生的向前推力，fN2为地面对桨叶轮的摩擦力。T为行星摇臂中心齿轮轴的转矩，T1为桨叶轮中心轴转矩，左右侧的T1和T相等，机器人受力如下：

2FN2+FN1+N2cosα=(m1+m2)g

(7)

2(F2-μFN2)-N2sinα=0

(8)

其中，μ为桨叶轮与地面及台阶的动摩擦系数。

以前摇臂轮中心轴为基准，对机器人进行力矩分析，可得：

(9)

2(T1+T)+N2[l1-(Lx-d2tanα)+Rcosβ]-

(10)

其中，F′为前摇臂质心沿桨叶轮质心的作用力。

对行星摇臂进行受力分析，可得：

(11)

(12)

联立式(7)～(12)得单侧转矩T与机器人结构参数之间的关系，即：

[l1-(Lx-d2tanα)+Rcosβ-rsinα]-

(13)

其中：i48表示越障轮内中心齿轮与桨叶轮之间的齿轮组传动比。

3 机器人越障机构优化设计与分析

对于前述机器人越障过程中的临界位置，在给定m1、m2、r、H和d2的条件下，优化设计机器人的结构与运行参数l1、R、α以及β，使机器人在越障临界位置所需转矩T最小，优化问题的目标函数如下：

f(α,β,R,l1)=|T|

(14)

其中T由式(13)推导求得。

选取H为150 mm，优化问题的约束如下：

(15)

摇臂内的齿轮组为加速齿轮传动，选取μ为0.8，1/i48为3.8，轮子半径r为60 mm。

采用MATLAB遗传算法求解上述问题，表1为优化前后结果对比。由表可见，优化后机器人所需l1相比优化前减少91.2 mm，所需中心齿轮轴临界越障转矩T相比优化前下降718.4 N·mm，机器人车体长度和所需转矩均减少11%左右。

表1 优化前后机器人越障所需转矩与结构参数Tab.1 The optimized structure parameters and required torque for obstacle climbing compared with the values before optimization

如表2所示为本文提出的轮鳍复合式机器人与其他两栖机器人的越障能力对比。表中列举了机器人高度h与试验越障高度H，其比值H/h代表机器人越障能力，比值越大，机器人攀越障碍的能力越强。可见，相比于文献中两栖蟹、两栖球及六弧形足两栖机器人，轮鳍复合式机器人能够攀越相比其结构尺寸更高的垂直障碍，说明其结构能较好地适应复杂地形，越障能力较好。

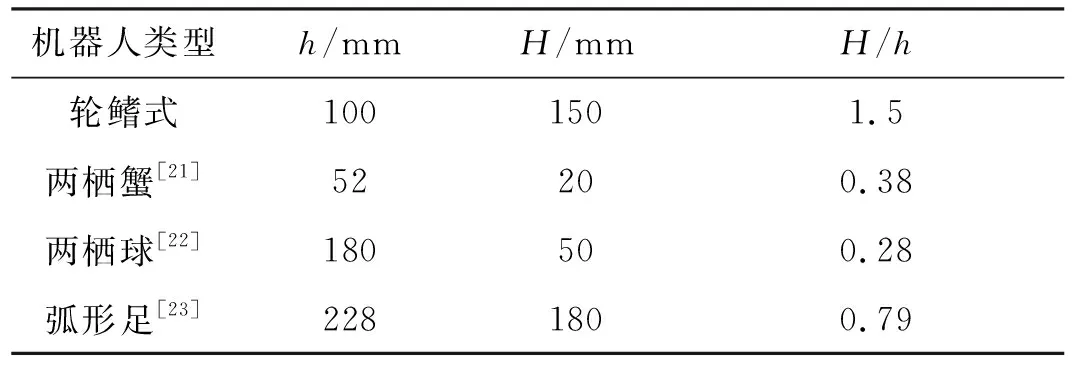
表2 轮鳍复合式两栖机器人越障能力与其他机器人的比较Tab.2 Comparison of the obstacle-climbing ability of the amphibious robot compounded with wheel and fin with other robots

如图5所示为不同β角下的机器人临界越障转矩的优化值Tmin，由结果可知，随着前摇臂与车体夹角β的增加，机器人临界越障所需转矩的最小值单调降低。当β为25°时，所需临界转矩最小，对应表1中的优化值。

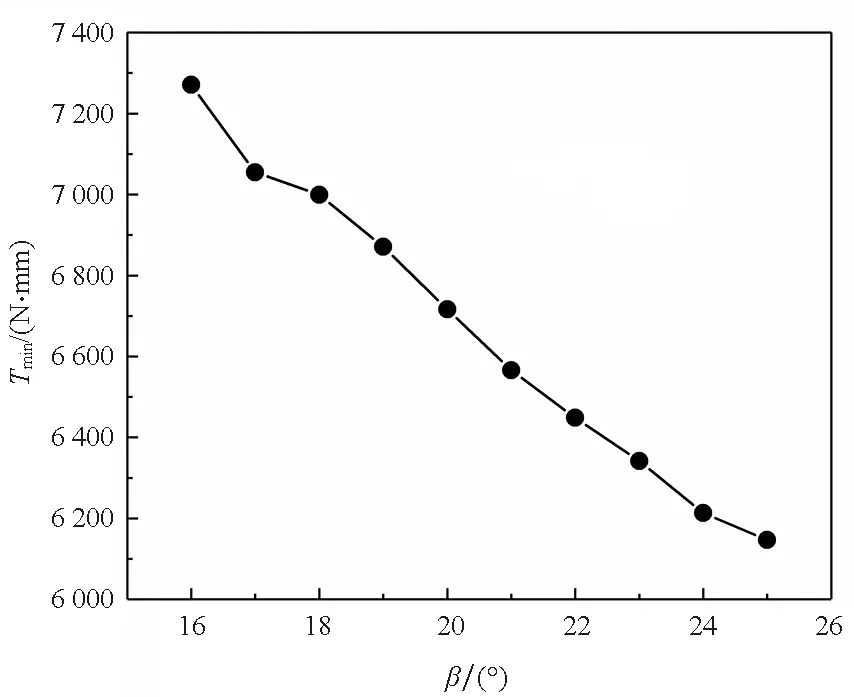
图5 机器人临界越障转矩随β的变化Fig.5 The critical torque of the obstacle climbing versus β

如图6所示为机器人在越障时前摇臂中心齿轮轴所需转矩T随俯仰角α的变化情况。结果表明，当机器人俯仰角α增加时，其所需越障车体长度增加，机器人越障所需转矩呈先减小后增加的趋势。在不同β角下，机器人越障所需转矩随着β的减小而增大，同时也印证了图5中的结果。

图6 机器人越障所需转矩随α的变化情况Fig.6 The required torque of the obstacle climbing versus α

如图7所示为机器人越障时地面、障碍物边缘对机器人的支撑力FN1和N2，以及桨叶轮转动时产生的向前推力F2随β的变化情况。由结果可知，当β角增大时，障碍物边缘对机器人的支撑力N2增加，地面对机器人车体的支撑力FN1降低，而机器人所受的前向推力F2维持在18 N左右。

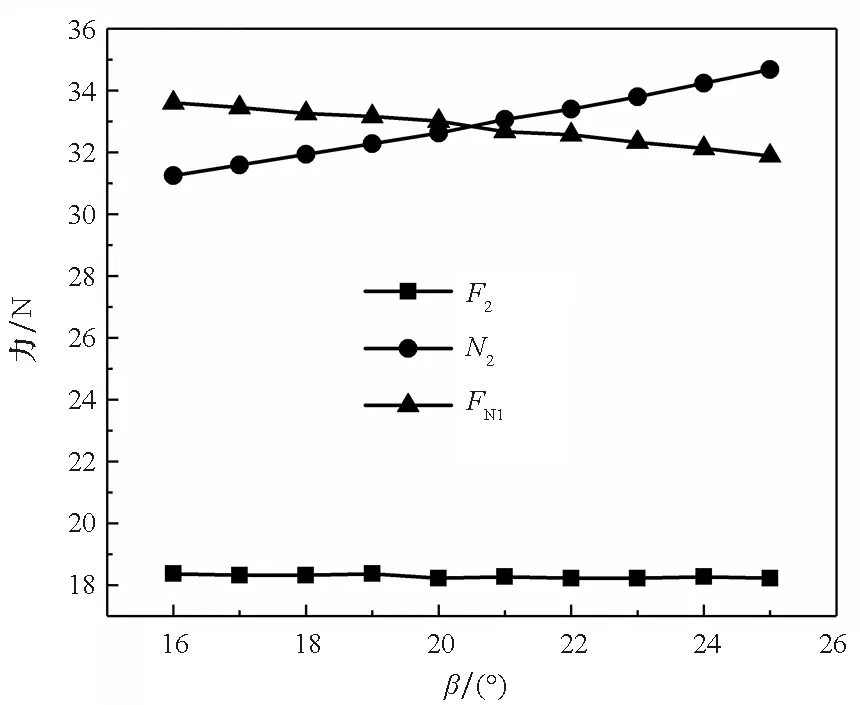
图7 机器人越障时的FN1、N2和F2随β的变化Fig.7 The FN1, N2 and F2 in the obstacle climbing versus β

如图8所示为FN1、N2和F2随俯仰角α的变化情况。结果表明，随着俯仰角α增加，障碍物边缘对机器人的支撑力N2由35 N减少至12 N左右，地面对机器人尾端支撑力FN1随之增加至50 N，可知俯仰角α对机器人越障时受力影响较大。

4 机器人研制与实验验证

4.1 机器人地面行进仿真分析

建模并进行Adams仿真实验如图9所示，障碍高度为150 mm，斜坡倾角为15°，机器人的电机转速500 (°)/s。

图9 机器人仿真示意图Fig.9 Simulation of the amphibious robot

图10所示为机器人位移和速度变化图，机器人在翻越障碍时，运动速度出现了一定的波动。越障过程存在越障轮翻转和前后轮交替支撑的现象，导致机器人运动速度不稳定，出现打滑。在爬坡过程，机器人克服自身重力，运动速度有所下降，整个过程中没有出现侧翻或者卡顿现象。

图10 位移和速度曲线Fig.10 Velocity and displacement of the robot

如图11所示为摇臂中心转矩随摇臂转角θ的变化情况，由结果可知，当摇臂转角从0°增加至200°的过程中，机器人接触垂直障碍并越过临界位置。在越障初始阶段，左右摇臂中心转矩先迅速增加，然后随着摇臂转角的增大而降低，转角为90°时转矩最小；当越障轮翻转超过90°时，后摇臂继续抬升车体，转矩又再次增大。

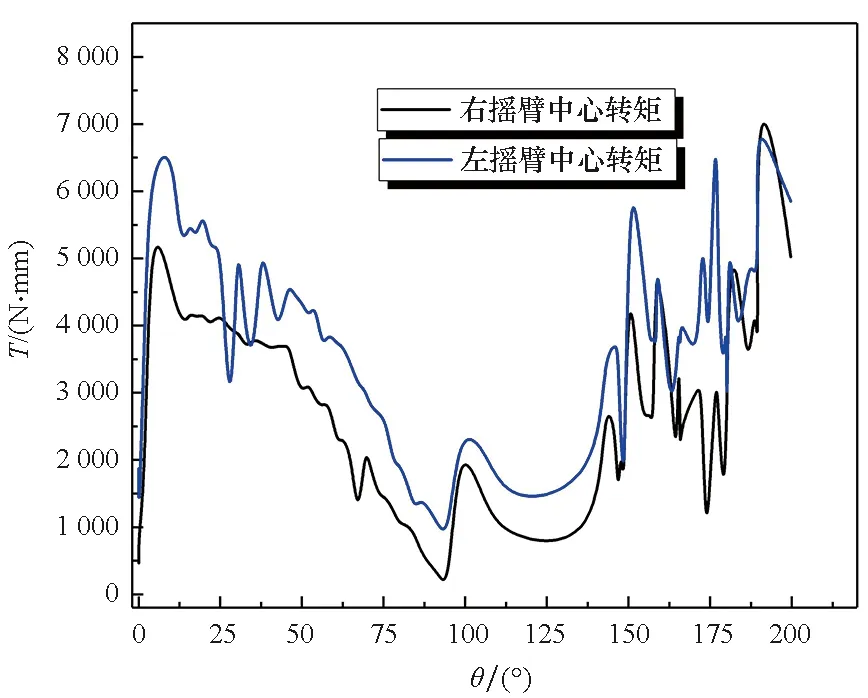
图11 摇臂中心转矩随运动角度的变化Fig.11 Torque of the rocker arm versus movement angle

如图12所示为越障过程中后轮、尾端万向球受力情况及摇臂中心转角随时间的变化。在Ⅰ阶段，机器人在平地前进加速运动，后轮和万向球的受力在10～20 N之间。在Ⅱ阶段，后轮被抬起，万向球所受地面支撑力增加，随后摇臂驱动桨叶轮从而带动车体攀越至障碍台阶上，直到尾端万向球与地面脱离接触。在Ⅲ阶段，后轮翻转搭上障碍并抬起尾端万向球，此过程持续2 s左右。在Ⅳ阶段，机器人在障碍台阶上且受力基本稳定。在V阶段，机器人爬坡，后轮和万向球受力增加。摇臂转角从0增加至190°，上坡过程维持在165°。

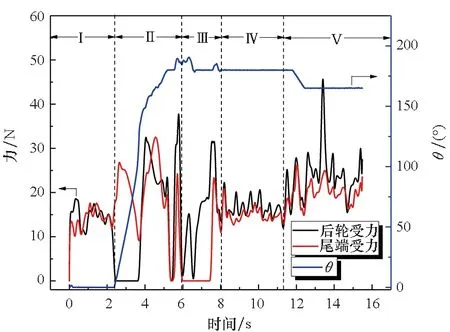
图12 机器人与地面接触压力曲线Fig.12 Contact force between the robot and land

4.2 样机试验

根据前文设计分析，选取最大扭矩为5 N·m、持续扭矩为2.8 N·m(500 r/min)的减速电机为动力源，研制了原理样机并开展越障试验，试验结果如图13和图14所示。由图可见，机器人行进过程中遇到垂直障碍或楼梯时，越障机构后轮翻转搭上障碍边缘，驱动机器人质心通过攀越，从而使整体攀越垂直障碍和楼梯，验证了前述设计。

图13 越障试验Fig.13 Obstacle climbing experiment

图14 爬越楼梯试验Fig.14 Experiment of climbing stairs for the robot

为验证两栖机器人水下运动性能，根据波动鳍的结构尺寸研制了波动鳍实验平台，其水下运动平台的试验结果如图15所示，可见，机器人水下运动速度随波动鳍频率呈线性增加的关系，当波动频率达到2 Hz时，水下推进速度达到300 mm/s。

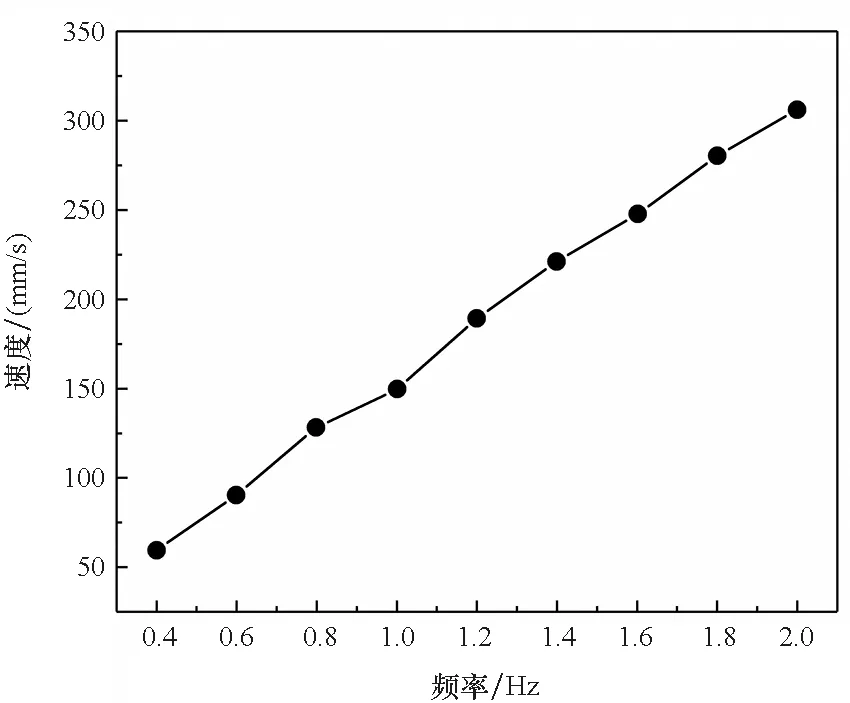
图15 水下运动试验结果Fig.15 Experimental measurements of the underwater propulsion

5 结论

1)通过将轮式运动和波动鳍波动两种运动型式进行组合，设计了轮鳍复合式两栖机器人的结构，并重点对越障机构的运动机理进行了分析，为机器人的设计提供了理论支撑。

2)基于质心运动学与机构力学分析，给出了机器人越障性能的优化设计方法，以机器人临界越障时所需转矩为优化目标，优化设计了机器人的结构与运行参数，结果表明，优化后机器人越障所需临界转矩相比优化前减少了11%左右。

3)针对机器人的行走与越障性能，通过Adams进行了仿真计算，获得了越障过程中运动速度与受力情况随时间变化的趋势，指导了越障机构的设计。

4)基于前述优化结构研制了实验样机，通过地面与水下试验验证了设计思路和方法。