基于KWAP-KNN分区聚类算法的室内定位分析
(河南工业贸易职业学院,信息工程系,河南郑州市,450000)张海霞
随着科技发展,定位技术发展越来越快,几乎延伸到了各行各业,人们对定位要求越来越精准,仅凭借全球定位系统(GPS)的室外定位已经无法满足人们需求[1-3]。因为移动通讯设备和Wi-Fi信号的广泛覆盖,基于Wi-Fi的室内定位算法凭借其成本低、定位精度高且无需其他外设等优点,逐渐成为现阶段的研究热点之一[4]。该定位方法在定位收集信号的过程中,基于Wi-Fi的室内定位仅依靠信号接受强度指示(RSSI)就可以完成定位,但由于障碍物遮挡、环境变化等多重因素引起的时效性、多径效应等问题,RSSI信号存在误差,在极大程度上影响着室内定位的精度[5]。因此,对基于Wi-Fi的室内定位研究十分必要。
1 分区聚类算法
1.1 WAP聚类算法
目前,通常可以选择在无线传感器网络(Wireless sensor network,WSN)应用系统中加入移动节点的方法来实现更加灵活地完成现场监测过程,但是如何对动态过程采用具备低能耗与高精度的WSN节点进行定位是现阶段众多研究人员需要解决的问题等。
AP聚类算法中以p作为节点为聚类中心的度量。由于环境、人员流动、多径效应等因素的影响,不同信号接收装置接收到RSSI信号值存在差异,仅凭借欧氏距离计算S,选取矩阵中值或者均值作为相似性度量,会导致定位结果不准确。针对上述问题,本文引入熵值法对S相似度进行优化后,对优化后的p进行加权处理,已获得更加准确的粗定位结果。
熵值法用来判断指标的离散程度。将每个节点的一组RSSI值作为输入计算权重,并将得到的权重作为不同信号接收装置对该节点的影响因子。其中,针对异质特征维数同质化问题,需要将特征维数的标准化处理。首先归一化处理数据,计算正向特征维数和负向特征维数数值。
正向特征维数:
负向特征维数:
将一组RSSI值作为输入,熵值法具体计算公式如下:
其中,RSSIij为指纹库中第i个数据点的第j个RSSI值,i=1,2,…,n;j=1,2,…,N,n为样本数,N为RSSI值数,j表示权重。则节点i,k之间的相似度计算方式为:
通过得到的权值计算数据点之间的相似度,对相似度进行均值加权处理,则p的值为:
1.2 基于KWAP-KNN算法原理及流程
距离信号发射装置越近,则RSSI信号接收更准确。且RSSI信号值在空间上区分能力有限,通常都在1m以上,所以为了避免相邻指纹信息在位置上二异性,两个信号发射装置布置距离应该在1m以上。以信号接收装置为圆心,根据实际环境确定覆盖区域半径,尽量保障大部分区域在划分的覆盖区域范围内。
区域划分依据为位置信息,选择K-means进行分区,该方法简单且容易实现,选取信号发射装置所在位置为K个聚类中心的位置,通过聚类对未覆盖区域和交叉区域进行分区。当对未知节点进行区域划分时,根据RSSI值差异确定归属区域,如果属于覆盖区域,直接进行WAP聚类,如果属于未覆盖或者交叉区域,通过K-means重新进行归类,当所有的节点被划分到不同区域时,划定小区域。最后通过KNN聚类在小区域内获取粗定位结果。整个区域划分及定位流程如图1所示。

图1 区域划分流程图
2 实验结果及分析
区域划分以实际室内环境和信号发射装置布置为准,以信号发射装置位置为圆心,固定距离为圆心,划分区域。实验在14m×11m的区域进行,现场布置了共6个路由器作为信号发射装置。
通过Matlab软件来仿真验证本文的定位算法。进行仿真测试时,按照表1数据来设定各项参数。在100m的范围内以随机方式设置共60个节点,将节点的通信半径设定为20m。节点分布图如图2所示。

表1 参数设置

图2 节点分布图
图3为AP聚类和WAP两种聚类的效果图。

图3 聚类效果图
选取一百组测试点进行实验,未进行区域划分之前,分别使用KNN、AP-KNN、WAP-KNN三种算法进行定位。可以得到如图4所示的误差累积图。图中可以看出,随着节点数目增加,WAP-KNN累积定位误差低于其余两种定位方法。

图4 平均误差累积
图5为三种定位方法误差累积分布图。100个参考点中,定位误差小于2.5m的概率,KNN、APKNN、WAP-KNN算中算法分别为72%、67%、62%,其中KNN算法概率最高。但是WAP-KNN算法所有参考点的定位误差均小于3.45m,AP-KNN均小于4.00m,WAP-KNN总体定位误差较小。而且APKNN和WAP-KNN这两种方法定位没有出现误差较大的点。之后对三种方法求解平均定位误差,并对其最小最大误差进行分析,可得如表2所示的定位误差表。从表中数据看出,WAP-KNN算法的平均误差、最大最小误差值都比其余两种算法要小。

图5 三种定位方法误差累积分布图
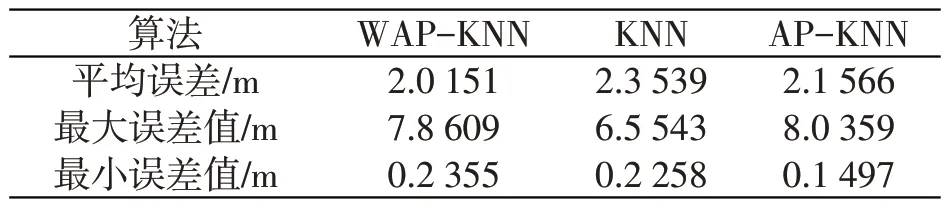
表2 三种定位算法定位误差表
3 结语
综上所述,针对单一聚类算法存在的多种问题,提出一种基于KWAP-KNN的分区聚类算法。实验结果证明,无论从样本点的之间相似性,还是从聚类时间来讲,WAP聚类算法都比AP聚类算法低,聚类效果更好。区域划分后,KWAP-KNN算法得到的粗定位结果更准确,定位精度可达到1.8m左右。

