“画数学”：发展学生几何直观能力的教学实践

江苏省南京市江宁开发区学校 刘 婷

一、缘起

（一）学生直观理解数学的能力亟待提高

教学中，我们常常要求学生对较复杂的数学问题采用画图的方式来分析和理解，可现实往往并非如此。学生缺乏主观能动性，尽管教师一遍遍强调要多“画一画”，但学生仍然很少画。其实，学生没有真正体会到构造几何直观对数学学习的作用。因此，在数学教学中，教师要充分借助形象直观的手段，实现从直观到抽象的跨越，使抽象的数学知识得以形象化、直观化，提升学生的数学思考能力，发展学生的几何直观能力。

（二）基于学科本质，是数学教学的基本要求

在数学教学中，教师应当注重发展学生的十大关键能力，同时，几何直观在整个数学学习过程中也发挥着重要的作用。利用图形描述来分析问题，有助于学生把复杂问题变得简单、形象，从而直观地理解数学。“画数学”，不仅可以外显学生的思维过程，启迪学生获得知识的意义建构，而且能促进学生对数学知识的理解。

（三）实践课堂深度学习的重要途径

课堂上的深度学习不是把知识直接平移、灌输，而是让学生在教师的引领下，围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程。课堂上引导学生操作材料，帮助学生 “经历”知识的发生、发展和建构的过程，这样的“重新经历”可以促进学生思考知识发现与建构的社会背景，体验探索的思想历程、价值追求、评价知识以及知识的建构过程，这样经历的过程才是实践深度学习的重要途径。而“画数学”恰好可以让学生的思维外显，描述解决问题的路径和方法以及存在的疑惑。

二、教学实践

（一）多元表征，抵达概念本质

数是对数量的抽象，在具体的情境中认识数，有助于学生理解数的意义。学生需要经历从具体到抽象、从数学意义的理解到数学概念的形成。在小学阶段，学生的思维主要以形象思维为主，因此教学中，让学生依赖于具体的、形象的支撑可以加深其对数的意义的理解，从而深刻构建概念的本质。

教学片段：“小数的初步认识”

师：想办法表示0.1元。可以画一画、涂一涂。

学生基于已有的认知与经验，画出对0.1元的认识（见图1）。

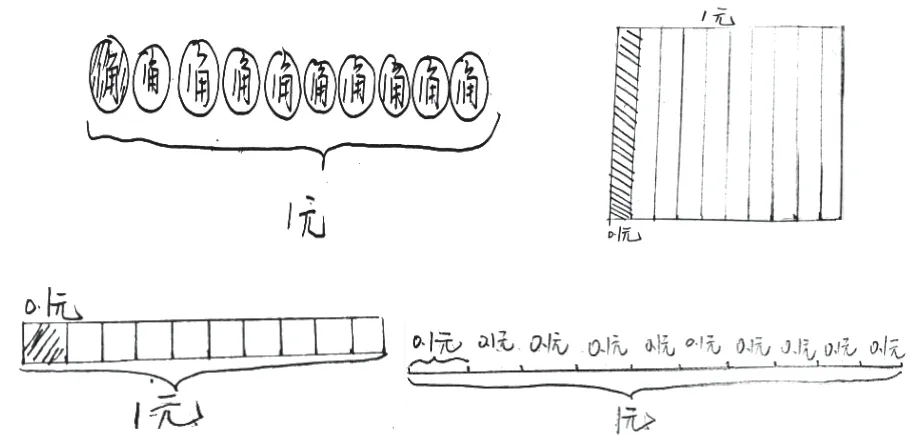
图1

师（追问）：这么多不同的作品中，有什么相同的地方，为什么都平均分成10份？

生在交流中得出：虽然画出来的图不一样，但都是把1元这个整体平均分成了10份，表示其中的一份，也就是1角，即十分之一元，小数表示是0.1元。

师相机出示图片（见图2）。

图2

师：在这个小长方形里除了可以找到0.1元，还可以找到哪些小数？在图上找一找、写一写、涂一涂，再说一说。

生交流后发现：十分之几就是零点几。

苏联心理学家和教育家赞科夫在《和教师的谈话》一书中指出，在儿童不能通过实物看见他所要了解的那些事物和过程的情况下，课堂上要赋予直观教学以显著的地位。小数对学生而言是抽象的，虽然看得见外在的形式，但摸不着它内在的本源，所以追根溯源，构建小数的意义十分重要。数学家弗赖登塔尔曾说，学习数学的唯一正确方法是实行再创造，也就是由学生把自己要学习的东西发现或创造出来。在上述教学中，学生基于已有的认知经验实现了再创造，展示丰富的思考结果，如10个“○”代表1元，每个“○”是1角，就是0.1元；直观的长方形、正方形以及线段图，形象、直观地表示出0.1元的含义。通过不同图形的比较，学生直观地理解0.1元的意义的过程变得生动。形的直观与数的巧妙结合，让学生主动沟通了十进制分数与小数的联系，抵达小数概念的本质——十分之几就是零点几，发展了学生的数学思考。

（二）画形明理，内化运算法则

数学新课标指出，在基本技能的教学中，不仅要使学生掌握基本技能的操作步骤与程序，还要使学生理解程序和步骤的道理。因此，在计算教学中，让学生明白算法背后的道理，学生才能更加灵活地运用运算法则。教师要充分考虑学生的认知特点以及数学本身的特点，采用生动、有效的几何直观手段，帮助学生理解算理，培养学生的几何直观能力，提升学生的运算能力。

如在教学“分数乘分数”时，教师出示例题，并让学生通过几何模型外显计算的过程，清晰展示计算的算理。

学生尝试画一画、涂一涂表示计算的结果，和同桌交流想法。

学生呈现图形（见图3），并说出思考过程。

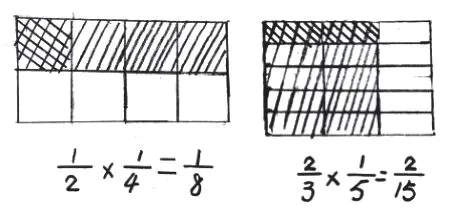
图3

算理是算法的依据，算法是对算理更高层次的提炼与概括。学生只有真正掌握了算理，才能在计算学习上学得更扎实、走得更远。在教学中，教师不仅要让学生知道“是什么”，还要明白“为什么”。分数乘分数的计算法则对学生来说比较容易掌握，学生即使不接受新课的学习，也可以依葫芦画瓢，完成计算。可是数学教学绝不仅仅止于会算，还要明白：为什么分数与分数相乘，分子相乘作为分数的分子，分母相乘作为分数的分母？教师引导学生尝试用图形描述的乘法意义，直观形象地理解“分了又分”——分母相乘的积作为分母；“取了又取”——分子相乘的积作为分子，学生对于算法的掌握和算理理解水到渠成。在计算教学中，让学生借助几何直观，可以把抽象的算理直观化、具体化，从抽象走向具体再到抽象，从而提炼算法，发展学生的运算能力。

（三）创造模型，深刻理解运算律

数学教学是为让学生拥有数学的眼光观察、数学的思维思考，以及建立模型思想。数学知识的学习过程，实际上就是对一系列数学模型理解和把握的过程。在教学中，笔者发现“乘法分配律”的掌握和灵活运用对学生来说是比较困难的。在教学实践中，学生要亲身经历乘法分配律的模型建构过程，引导学生自觉地用数学的方法去分析和解决实际问题。

如在教学“乘法分配律”时，教师可以这样引导学生创造几何直观模型，沟通“式”与“形”的联系。

出示例题情境（见图4），学生列式解决，通过计算发现两边结果相等。

图4

学生发现：（6+4）×24＝6×24＋4×24。教师让学生交流：除了可以通过计算发现两个算式的结果，还可以用什么方法说明结果相等呢？学生借助直观的点子图、矩阵图得出了结果相等的结论（见图5）。

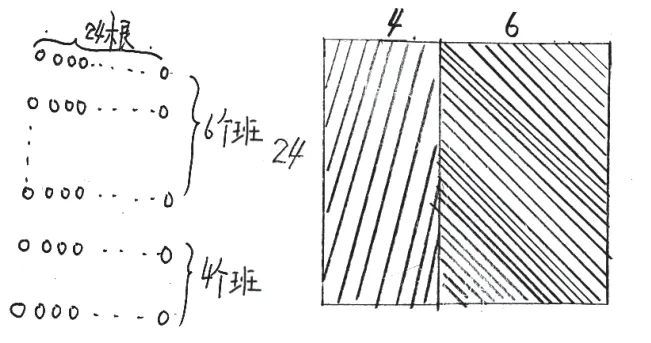
图5

将离散的点子图与图形面积相结合，丰富了学生的直观表现。

在此基础上，将长方形的长和宽改为字母（见图6）。

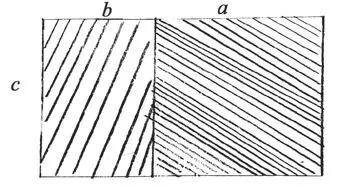
图6

这时，乘法分配律的几何模型应运而生，有助于学生加深对乘法分配律的直观理解，因为图中的a、b、c已经突破了整数的局限，长度也可以是小数和分数。

徐利治教授认为，直观就是借助经验、观察、测试或类比联想，所产生的对事物关系直接的感知与认识，而几何直观是借助基于见到的或想到的几何图形的形象关系产生数量关系的直接感知。让学生尝试用画一画的方式，通过数形结合，直观理解“先和再积”等于“先分别求积再求和”，逐步构建乘法分配律的“形”的雏形，接着通过不完全归纳，尝试总结、概括出乘法分配律“式”的表达，抽象出（a＋b）×c＝a×c＋b×c，构建出乘法分配律的几何模型，不断提升学生的直观理解能力。显然，其他运算律的教学也可以如法炮制。

（四）丰富评价，提升思维品质，形成思考模式

在教学实践中，让学生通过画图等方式参与学习的过程，是有视觉参与的一种思维方式。高阶思维的一大特征是评价，使思维外显，反省外显。评价是基于证据的推理和判断，而评价学生的思维能力，就是需要学生思维的外显，以思维品质的发展作为参考，如关注学生思维的清晰度、准确性、关联性以及深度、广度、逻辑性等方面。

如学习分数乘除法时，学生不太清楚单位“1”“量”与“率”等问题，教师可以设计以下题组，让学生通过画图表示问题中的数量关系。（见图7）

图7

通过画对比图，使学生的思维更清晰，从而更好地理解知识、掌握方法。（见图8）

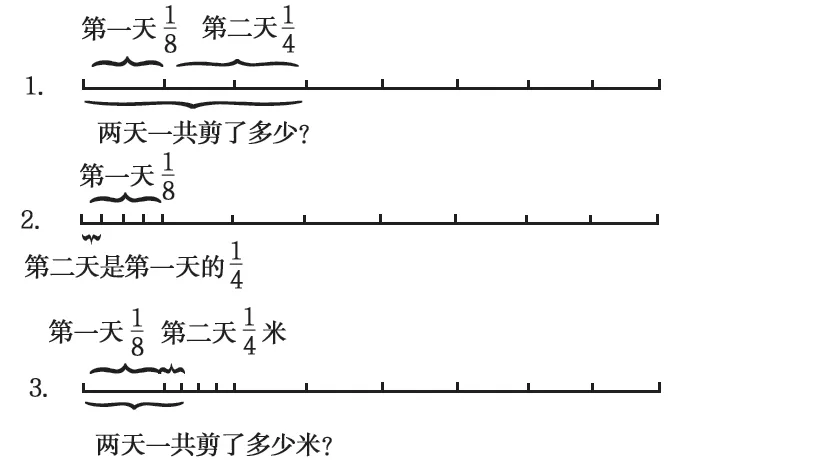
图8

如学习完负数，教师可以让学生“写一写或画一画对负数的认识”，加深对负数的理解，发展思维的准确性。在数学百分数后，教师可以通过问题发展学生思维的广度，如“这个问题与之前遇到的什么问题有关”，学生在画一画中思考，沟通外联，体现思维的广度，重新建构认知结构，针对学习中的难点，学生画图分析，呈现思考过程，展示思维的深度。“关于圆的面积计算公式，教材中将图形转化成平行四边形，还有别的方法吗？根据自己的经验，能不能画图说明？”这几个问题关注了学生的思维过程，使学生的思维更具逻辑性……

教学实践中，教师让学生经历“直观地看”“丰富地想”“形象地画”等思维过程，将抽象的数学知识等用图示表征出来，丰富了学生的个性体验，帮助学生积累了课堂学习的情感体验，转变了学生学习的方式，提升了学生的思维品质及几何直观能力，增强了学生的学习能力。

几何直观能力的培养，有助于提升学生的直观感知水平、直观理解水平，然而“画数学”，不仅能让学生的思维可视化，还能培养学生逐步形成构造直观的能力，养成用数学的思维方式分析问题、解决问题。纵观整个小学阶段，其实在一年级的教学中，很多教师就已经让学生学习用画图的方式表示数，表示计算的结果，后面的学习中让学生画示意图、线段图、长方形等图示表征出对概念、算法及运算律等数学知识的理解，借助画出的“形”来描述和分析，直观地理解数学本质知识。教学实践表明，让学生“画数学”的过程，就是让学生拥有构造几何直观的能力，也能发展学生的几何直观能力，对提高他们解决问题的能力都有显著的效果。