水下结构激振力与辐射声压关系的验证

王永富

（中国人民解放军海军91970部队，辽宁大连 116041）

0 引言

在研究水下结构的振动和声辐射时，不可避免会涉及流固耦合问题，对流固耦合规律的认识程度是实现对水下结构振动和声辐射预报的关键。文献［1］、文献［2］分别阐述了声学和流体力学的基本原理，文献［3］研究了有限元的声辐射，文献［4］、文献［5］则提出附加阻尼质量法，采用FORTRAN 代码计算外域流体附加质量和附加阻尼矩阵，采用结构有限元分析程序对结构和内域流体作有限元分析，采用DMAP 代码将附加质量和附加阻尼同结构质量矩阵和阻尼矩阵相叠加，实现了流固耦合计算。文献［6］依据不同域的特点，结构和流体内域采用有限元方法、流体外域采用边界元法，研发了计算水下大型结构流固耦合振动和声辐射的计算程序。一些学者认为水中结构流固耦合振动及其声辐射是一个非线性问题，然而大多数研究这一问题的文章均采用线性方程进行求解。本文着重对小振幅振动时的流固耦合系统进行研究，对激振力和辐射声压的关系进行数值和试验验证，深化对水下结构耦合振动规律的认识。

1 基本理论

结构在流体中振动时，本质上就是结构振动和流体的耦合。忽略介质对声波的粘性吸收，假定介质为均匀的理想流体，略去介质的热传导作用，考虑介质中传播的是小振幅波。在定解条件：固体壁面上的边界条件、有界条件、辐射条件下，由这些条件可以得到以速度势φ 控制的方程如下[5]。

式（1）是一个关于速度势φ 的线性定解问题，所以其描述的结构与流体耦合振动所组成的是一个线性系统。

2 试验验证及数值仿真

2.1 试验模型介绍

制造了一个加肋圆柱壳，在圆柱壳内部设计了基座和9 条等间距分布肋骨，在基座上方安装激振机（图1～图2）。其中，圆柱壳长1000 mm、直径800 mm，肋骨尺寸5 mm×25 mm，肋骨间距100 mm；基座面板375 mm×200 mm，端盖、壳体厚度分别为10 mm、3 mm；所用材料密度为7.85×10-9N/mm3，杨氏模量为206 000 N/mm2，阻尼、泊松比分别为0.06 和0.3。

图1 加肋圆柱壳模型

图2 基座及激振机布置

2.2 模型水下布置

对于水下结构声辐射的测量，比较理想的环境是消声水池或开阔的湖泊。本次试验是在某水库中进行，背景噪声较低，是比较好的声场环境。用压载铁对圆柱壳进行压载，并用软绳连接至双体船使圆柱壳在处于悬浮状态。模型水下布置见图3：圆柱壳轴线距离水面5 m（Z），水听器距离模型中心6.8 m（r）。在试验船的首部和左舷放置水听器（图4）。

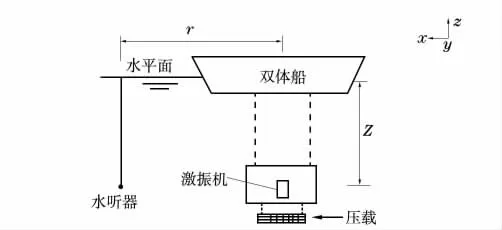
图3 试验模型水下布置

2.3 数值仿真

（1）对圆柱壳模型进行数值仿真，采用结构有限元耦合流体边界元方法并利用有限元软件PATRAN/NASTAN计算水下结构振动与声辐射[6]，在指定激振频率下计算不同激振力幅值时的辐射声压。

（2）有限元网格见图5，在基座面板施加垂向激振力F（图6），数值计算采用的圆柱壳模型材料属性见上文。

图5 模型有限元网格

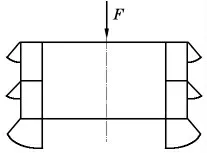
图6 激振力示意

（3）流体密度ρ 为1020 kg/m3，流体中声速c 为1450 m/s。

（4）模型放置的位置和声场计算点与试验状态完全相同（图3、图4）。

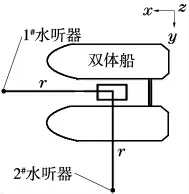
图4 水听器布置

2.4 数值仿真与试验结果对比

试验时，在指定激振频率下通过改变激振力的幅值得到对应状态下的辐射声压。图7 和图8 分别是激振频率为128 Hz 和155 Hz 时激振力与辐射声压响应曲线。由图可知，试验测得1#和2#水听器的激振力辐射声压关系曲线基本符合线性关系。数值计算结果同样表明激振力与辐射声压符合线性关系。

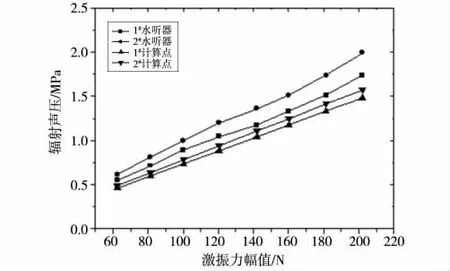
图7 128 Hz 激振频率下激振力与辐射声压关系

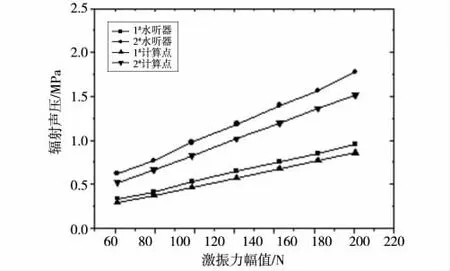
图8 155 Hz 激振频率下激振力与辐射声压关系

对比数值计算和试验测得的辐射声压值，换算为辐射声压级后最大不超过6 dB，导致这种误差的因素主要有圆柱壳建造焊接过程中的工艺对阻尼因子的影响、水中背景噪声的影响等。

上述结果表明，激振力和辐射声压是线性关系，从而验证了理论分析的结果。

3 结论

本文通过水下加肋圆柱壳振动与噪声试验，并采用有限元耦合流体边界元法进行了数值仿真及声辐射计算，结果表明，在指定激振频率下激振力和辐射声压呈很好的线性关系，验证了小振幅振动时壳体结构与流体耦合振动所组成的是一个线性系统这一理论。