基于滑轮组和永磁弹簧的变刚度关节设计与控制
张 明 马鹏菲 孙 凤 孙兴伟 徐方超 房立金
(1.沈阳工业大学机械工程学院, 沈阳 110870; 2.东北大学机器人科学与工程学院, 沈阳 110169)
0 引言
随着机器人参与人类日常生活生产的增加,机器人的人机交互安全性和环境适应性问题越来越受到重视。相较于传统的刚性机器人,变刚度机器人具有更好的环境适应性,并在人机交互中具备更好的安全性[1-3]。因此变刚度机器人一直被海内外学者所关注与研究。经过多年的探索,目前柔性变刚度机器人主要分为:具有柔性变刚度机械结构的机器人[4-5]和利用弹性材料产生刚度变化的机器人[6-7]。其中采用机械结构实现机器人刚度变化的变刚度方式,使用最为广泛。例如AWAS(Actuator with adjustable stiffness)系列[8-9],CompAct-variable stiffness actuator (CompAct-VSA)[10]、Hybrid variable stiffness actuator (HVSA)[11]、Variable stiffness joint (VSJ)[12]、Active variable stiffness elastic actuator(AVSEA)[13]等结构通过改变杠杆支点与输出末端之间弹簧的距离实现变刚度。Mechanically adjustable compliance and controllable equilibrium position actuator(MACCEPA2.0)[14-15]、Parallel-type variable stiffness actuator (PSVA)[16]等结构则应用特殊曲面实现刚度的变化。OSADA等[17]设计的人型机器人“Kojiro”中为其关节处加入了柔性变刚度模块,首次提出了线绳驱动变刚度模块被世界广泛认可,在变刚度关节研究中开辟了一个新的方向。文献[18]以非线性弹性元件(Nonlinear spring tension unit,NST)为基础,进一步的研究设计出了FAS(Flexible antagonistic spring)结构,其原理是使定滑轮位置可以发生变化,使原有的固定三角形结构随着拉力的变化而改变,从而实现更强的刚度变化。YONG-JAE等[19-21]基于NST线绳驱动的理念设计了LIMS(Low inertia manipulator with high stiffness and strength)系列7自由度机械臂,并在关节部分运用滑轮组结构,实现了输出倍数增长的效果和手腕处大范围转动。由于目前存在的机器人关节仍无法实现同时满足刚度变化范围、关节转矩和转动范围3种参数的最优化设计,为了进一步提高关节性能,需要不断对关节进行优化设计。
为了使变刚度机器人肘关节具有更接近人体肘关节的运动范围,同时具有更优良的刚度变化能力,本文设计一种基于永磁弹簧、滑轮组和类行星轮系结构的线绳驱动的变刚度机器人肘关节,阐述机器人变刚度肘关节的实现原理和机械构成。建立变刚度肘关节的刚度模型,以解决并联式绳驱变刚度肘关节的位置与刚度耦合的问题。以变刚度关节的动力学模型为基础,设计变刚度肘关节的刚度与位置的解耦控制器,并进行解耦验证和位置控制实验等,以验证变刚度机器人肘关节设计合理性和方案可行性。
1 变刚度肘关节原理分析
1.1 磁弹簧变刚度原理
图1为磁弹簧变刚度模块内部结构。通过将两块参数相同磁极相对的永磁环同轴心布置在变刚度模块的支撑结构和滑动导柱上,并在两个结构上分别设置定滑轮,当依次穿过其中的线绳受力变化时,线绳拉动滑动导柱使两永磁环之间的气隙Z不断减小。当两个永磁环逐渐靠近时,由于气隙变化产生的斥力F呈非线性变化来对抗线绳的拉力。动滑轮、定滑轮和绕在期间的线索呈等腰三角形布置,线绳长度变化量Δl随着气隙Z减小呈非线性关系增加。线绳上的拉力T随着气隙变化呈更强的非线性关系变化。因此在不改变线绳拉力的情况下,增加了线绳刚度变化范围。根据刚度公式并结合虚位移原理,变刚度模块的非线性刚度变化关系为

图1 磁弹簧变刚度模块Fig.1 Variable stiffness module of magnetic spring1.直线轴承 2、4.钕铁硼永磁环 3.滑动导向槽
(1)
式中k——刚度
1.2 动滑轮组原理
根据动滑轮力学特性,在肘关节内部(图2),将动滑轮组对称布置在转动盘两侧。滑轮组中一端固定在大臂定转动盘上,另一端固定在小臂动转动盘处,并随小臂转动。动转动盘和连接在其几何中心的支撑架,形成类似于行星轮和行星架结构。当其中一组动滑轮组受到拉力Tj时(j=1,2),可以推导求得滑轮组对小臂转动盘的拉力为

图2 肘关节内部绕线结构Fig.2 Internal wires structure of elbow joint
τ′=nηTj
(2)
式中η——线绳拉力方向矢量
n——滑轮组中线绳缠绕圈数
τ′——小臂转动盘拉力
因此电机对小臂的驱动力矩被放大n倍。
2 变刚度肘关节样机实现
基于以上两种原理设计了变刚度机器人肘关节结构三维模型,如图3所示。两套线绳驱动系统对称布置,线绳的一端固定在动滑轮上,依次穿过变刚度模块、线索导向结构,另一端固定在与电机固连的线绳绞盘上。整体肘关节通过控制两台电机的转动角,带动两根线绳实现收紧与放松过程,分别完成变刚度模块中磁环间隙减小和带动两片转动盘完成相对类啮合转动,实现对肘关节的位置和刚度控制。其中在关节的状态参数发生改变时,关节转动将会引起线绳长度变化,但磁弹簧变刚度并不会受关节转动而发生改变。两组滑轮组结构以圆心点O0和O1对称布置,形成和人体手臂肌肉相似的拮抗式结构。如图4所示,根据以上设计思想加工了变刚度关节样机。整体结构中使用线绳传动可以使电机后置,同时各零部件在设计中应用轻量化设计理念,有效减小了小臂质量。此种布置方式可以应用到多自由度复杂操作臂中,通过线绳驱动多级关节可以减小关节对电机性能的需求。在变刚度关节中,线绳转向的部分均使用滑轮作为导向,并在线绳转向处,滑轮均为中线相切布置,保证线绳传递的稳定准确。检测关节转角的编码器与转动保持架同步转动,实时检测关节转角,并推算出对应肘关节的实际运动位置。
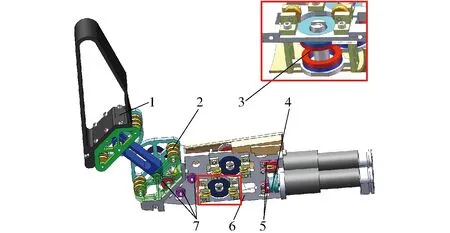
图3 肘关节三维模型内部结构图Fig.3 Internal three-dimensional structure of elbow joint1.小臂 2.动滑轮组 3.磁弹簧变刚度模块 4.线绳绞盘 5.传动支架 6.大臂 7.线绳导向机构

图4 肘关节样机Fig.4 Elbow joint prototype
3 肘关节刚度模型建立
根据关节结构设计布置可知,变刚度关节只在二维平面内运动,因此在平面内建立变刚度肘关节的坐标系如图5所示。基坐标系O0{x0,y0}位于固定转动盘的圆心处,动坐标系O2{x2,y2}位于与固定转动盘啮合的动转动盘的圆心处,且y2与小臂轴向方向同向。动坐标系O1{x1,y1}位于类行星架的末端,且y1与行星架的轴向方向同向,类行星架长度是固定转动盘圆心到动转动盘中心的距离。行星架随着动转动盘的啮合旋转而转动。由于两片转动盘半径相等,因此小臂旋转角度θ是类行星轮系结构转动角γ的2倍,即θ=2γ。

图5 肘关节二维平面简图Fig.5 Two-dimensional plan of elbow joint
通过对肘关节进行静力学特性分析可以降低后续计算的复杂性,由于两片转动盘可以形成类啮合转动,所以两片转动盘的转动接触点始终在O0O2连线上。对转动盘接触点,通过取矩可得关节在转动范围内任意位置时静力力学等式为
τ1r1+τ2r2-Grg=0
(3)
式中τ1——红色纯绳拉力G——小臂重力
τ2——蓝色线绳拉力
rg——小臂重力瞬时力臂
r1——红色线绳瞬时力臂
r2——蓝色线绳瞬时力臂
根据转动结构设计,在关节静力学简化模型中,变刚度肘关节的两片转动盘转动接触点O1始终在类行星轮系的圆心线O0O2上,使关节呈类啮合方式转动。对点O1取矩,根据肘关节内部结构,结合静力学平衡方程推导得到2条线绳作用力与小臂重力之间的关系式为
(4)
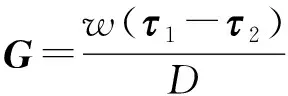
式中D——类行星轮系中圆心线O0O1距离
w——肘关节内部对称布置的两滑轮组之间的距离
联立式(3)、(4)可得肘关节运动方程为
(5)
式中J1——关节转动惯量
Bi——系统阻尼
变刚度肘关节中,驱动电机作为驱动输入单元,通过控制线绳变化实现各模块工作,由于变刚度肘关节中各传动部位均设置导向传动结构,所以线绳驱动系统中各模块线绳上的拉力近似相等。由此可将输入肘关节内部的线绳拉力近似看作磁弹簧变刚度模块中线绳的输出拉力,结合动滑轮的力学特性得到肘关节滑轮组对小臂作用的线绳拉力的近似表达式为
(6)
结合虚位移原理,当假设给定一个极小的输入转矩,变刚度肘关节小臂输出端将会产生一个极小的转动角,此时关节力学表达式为
(7)
通过式(7)的变形推导,可以得到变刚度肘关节的刚度矩阵Kθ。根据虚功原理得到
(8)
在肘关节中,通过控制线绳长度实现关节位置与刚度控制,将磁弹簧变刚度模块中线绳拉力Tj与转动角θ之间的关系变换为拉力Tj与线绳长度之间的关系
(9)
式中kj——变刚度模块刚度
lj——线绳驱动磁弹簧模块中线绳长度
ηj——线绳拉力方向矢量
将式(8)、(9)代入式(7)整理可得
(10)
式中 Δl1、Δl2——变刚度模块刚度变化引起的线绳长度变化量
为了实现肘关节位置-刚度的解耦控制,需要对关节转动而引起的线绳变化量Δlj进行分析求解。如图5所示,肘关节在初始平衡位置时,两条线绳的长度L0等于两转动盘圆心距,且两套滑轮组中滑轮圆心连线均平行于转动盘圆心线。在肘关节转动过程中,根据不同的转动方向,两根线绳分别进行张紧和收缩变化。从坐标系{O1}变换到坐标系{O2}时,点a1、b1相对坐标原点转动相同的角度运动到点a2、b2处,两根线绳长度变化量始终相同。推导线绳长度变化量与肘关节转动角之间的函数关系为
ΔL=|Lj-L0|=nwsinγ
(11)
式中Lj——肘关节转动到平衡位置之后的线绳长度
实际的关节样机在安装滑轮组时,线绳在肘关节中的缠绕方式分为水平缠绕和斜向缠绕两种,则式(11)可以变换为
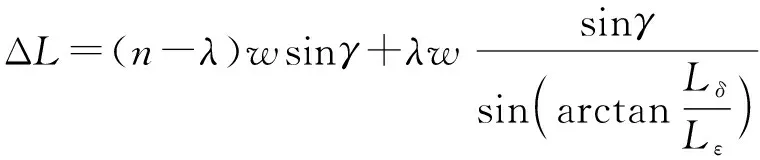
(12)
式中λ——斜向缠绕线绳数量
Lδ——O0O2圆心距
Lε——同一滑轮组中相邻两滑轮的间距
分析在不同刚度条件下,肘关节转动任意角度所引起的两根线绳长度变化。联立式(10)和式(12)可以实现变刚度肘关节位置和刚度的独立控制。
通过对关节位置与线绳长度的对应关系求导可以得到线绳速度与关节速度的对应关系为
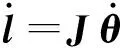
(13)
其中
(14)
式中J——机器人雅可比矩阵
根据关节转动角和磁弹簧变刚度模块可得整体肘关节的刚度模型为
(15)
为了得到变刚度关节的刚度变化规律,对式(15)进行理论计算分析。当线绳伸长量从 0 mm 变化到18.16 mm,即永磁弹簧刚度从 1.51 N/mm 变化到无穷大。根据式(1)理论上肘关节刚度变化范围从13.25 N·m/rad变化到无穷大。根据结构的布置设计,变刚度关节理论有效转动范围可以从-90°运动到90°。以关节线绳长度变化量16 mm条件下为例,如图6所示,关节位于不同位置时,关节刚度随着永磁弹簧刚度的增加呈非线性规律增加。关节刚度随着关节位置变化呈抛物线规律增加,且随着永磁弹簧刚度的增加,关节刚度随关节位置变化曲线陡峭程度增加。关节位于对称中心位置附近时可以实现刚度的调整范围最大,随着关节位置趋近两侧极限位置,关节刚度变化范围在减小。当前条件下,如图6a所示,磁弹簧变刚度模块的刚度变化范围为1.51~78.22 N/mm,如图6b所示肘关节刚度范围为13.25~6 210.9 N·m/rad。

图6 刚度模型仿真计算结果Fig.6 Simulation and calculation of stiffness models
4 关节动力学分析与控制器建立
4.1 动力学建模
为了实现变刚度肘关节刚度和位置的解耦控制,对关节进行了动力学建模。假定不考虑线绳自身弹性形变,通过在二维平面内建立关节简化模型,根据式(5)、(6),结合拉格朗日平衡等式建立整体关节动力学模型为
(16)
式中JM——电机惯性矩阵
R——电机上绞盘半径
ζj——线绳拉力方向矢量
TM——电机驱动力矩
η′——线绳拉力提升系数
JT——小臂输出转动惯量
4.2 控制器设计
根据变刚度肘关节的驱动原理,当线绳驱动整体关节发生运转时,关节会同时产生转动角和刚度的变化,从而使关节的位置和刚度参数发生耦合。为了实现更好的关节控制效果,设计变刚度肘关节刚度位置解耦控制器。以变刚度肘关节的工作原理作为基础,设计如图7所示的开环控制器,将肘关节的期望刚度Kd与期望转动位置θd作为控制器的输入,刚度模型中应用牛顿迭代法对由关节刚度变化引起的线绳变化量Δlj进行求解,根据式(12)得到关节由于位置变化产生的线绳变化量ΔLj,进行叠加后输入电机绞盘。则可以得到输入电机转角分别为
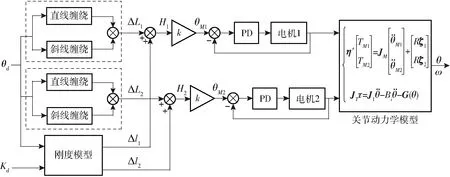
图7 肘关节解耦控制流程图Fig.7 Elbow decoupling control flow chart
(17)
式中Hj——线绳驱动系统中输入电机绞盘的总线绳长度变化量
经过计算得到相对应的线绳变化量,进行叠加得到总变化绳长Hj并通过线索绞盘转换成电机转角θMj,输入PD控制器调节电机Mj转动角,并将调节结果负反馈与初始值对比形成闭环控制系统。将得到的电机转角输入肘关节动力学模型,实现通过双线绳驱动系统实现关节的位置与刚度的解耦控制,从而得到关节转动角θ和转动角速度ω作为输出。
5 变刚度肘关节实验
磁弹簧变刚度模块中永磁环的主要参数如表1所示,肘关节结构中主要参数如表2所示。为了方便后续计算,对仿真得到的数据进行曲线拟合。仿真得到的拟合函数关系式为

表1 永磁环参数Tab.1 Parameters of permanent magnetic rings

表2 关节主要参数Tab.2 Main parameters of joint
τ=0.008 0Δl4-0.078 61Δl3+
0.157 32Δl2+1.51Δl+4.833 4 (18)
实验台搭建如图8所示,通过在上位机中应用Matlab/Simulink软件编译搭建的控制框图。在控制器DSpace1103中,分别将控制输入信号转换为电压信号,然后分别输入到两个驱动器ESCON70/10中,随后转换为电流信号控制伺服电机转动。在关节内部设置的编码器和驱动电机的编码器返回检测信号,可以实时检测关节和电机的实际转动角。
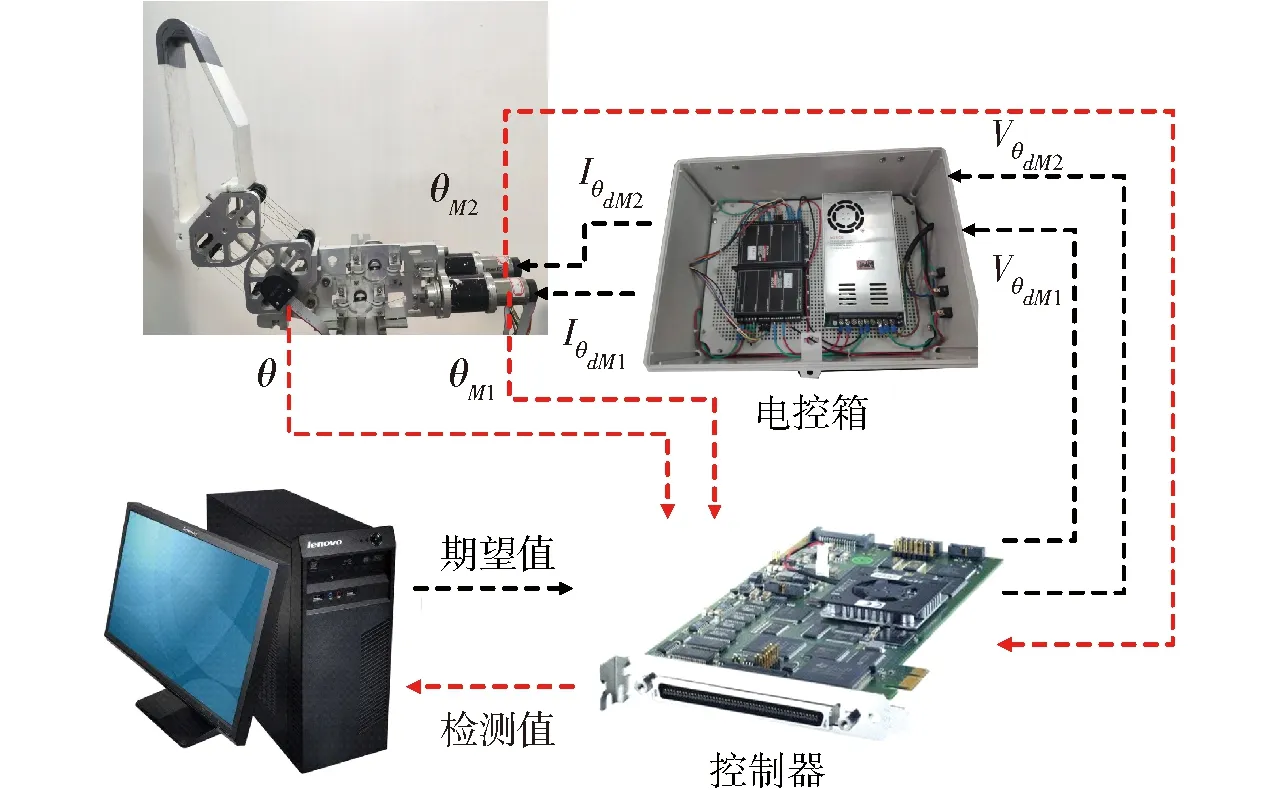
图8 肘关节实验平台示意图Fig.8 Schematic of elbow experiment platform
对比实验测试数据与现有的关节设计,如表3所示。相比于VSJPMM结构和LIMS结构,本文设计的肘关节可以同时具备转动范围大、刚度变化范围大的优点。并在此前提下,整体手臂质量减轻40%左右。

表3 肘关节性能参数Tab.3 Elbow joint performance parameters
5.1 关节解耦阶跃响应特性实验
变刚度肘关节位置和刚度解耦控制验证实验中,在肘关节输出小臂末端放置0.3 kg的负载以检测关节在不同状态条件下静刚度,对测量数据求取平均值并于期望关节刚度条件进行对比验证,检测静刚度与期望刚度误差在4%以内。首先将关节放置于初始位置,在解耦实验中对肘关节分别输入刚度阶跃信号与转动角阶跃信号,信号输入顺序为:刚度K1=50 N·m/rad,关节平稳后,在此刚度条件下输入期望转动角Δθ1=15°。待关节运动到-15°后,输入期望刚度K2=100 N·m/rad,并在此刚度条件下输入期望转动角Δθ2=15°。通过关节转角编码器与电机上的编码器返回检测值,如图9所示。 图9a 为转角编码器测量变刚度肘关节在输入不同信号条件下关节的位置轨迹。图9b为两台驱动电机的编码器在不同条件下输入阶跃信号后产生电机转动时所得到检测值。由于关节结构的设计,两台电机由于刚度引起转动时转动方向相同,且在关节中对称布置的磁弹簧变刚度模块同时进行刚度调整且刚度变化引起的线绳变化量基本相同,使关节所处的位置理论上不会发生变化。在不同刚度条件下时,关节响应特性也随刚度的增大有所提升,关节转动均可达到近似期望位置,肘关节的运动误差均在2.3%以内。当肘关节在刚度K2=100 N·m/rad条件下,关节运动的超调量相对更小,且关节运动达到平稳性的时间也更短,约为0.29 s。

图9 关节刚度位置解耦实验结果Fig.9 Joint stiffness position decoupling experiment
5.2 轨迹跟随实验
关节水平放置于初始位置,对关节输入连续正弦信号,振幅从-20°变化到20°,运动周期为6.3 s,小臂输出端长度为240 mm。通过两台电机联动,使关节呈正弦连续性摆动。分别在刚度K3=30 N·m/rad和K4=100 N·m/rad条件下,对肘关节进行连续性关节轨迹实验,如图10所示。由图10可知,在更大的刚度条件下变刚度肘关节运动时,关节运动位置相对于理想轨迹具有更好的运动跟随效果,且误差超调量也相对更小,说明刚度参数的设置对关节的连续性运动具有较为明显的影响。但关节刚度增加后,肘关节会在极限位置存在运动轨迹的误差,这是由于磁弹簧变刚度模块的拮抗式设计,使肘关节运动中,磁弹簧变刚度模块会抵抗线绳拉力的瞬时变化,导致关节在极限位置受到较大的阻抗力。
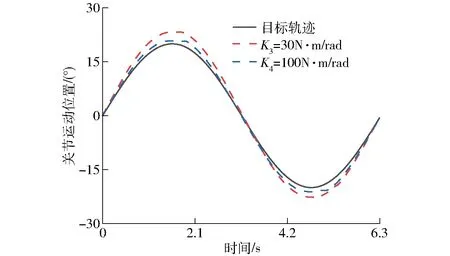
图10 正弦轨迹跟踪实验结果Fig.10 Sinusoidal trajectory tracking experiment
6 结论
(1)基于永磁弹簧、滑轮组和类行星轮系结构,提出了一种新型变刚度机器人肘关节。描述了运动控制过程与解耦控制器设计,并建立了三维模型与实物物理样机。
(2)利用模型间静力学关系和雅可比矩阵得到肘关节的刚度模型,并得到关节刚度随磁弹簧刚度和关节位置变化的规律。利用关节刚度模型和动力学关系,建立了变刚度关节解耦控制器,实现肘关节刚度和位置解耦控制。
(3)通过变刚度关节位置响应和轨迹实验得到变刚度关节位置控制精度和响应速度随着关节刚度的增加而增加的变化规律。

