河套灌区土壤质地克里金插值与平滑效应校正

万核洋 齐泓玮 尚松浩

(清华大学水沙科学与水利水电工程国家重点实验室， 北京 100084)

0 引言

土壤是与人类关系最为密切的环境要素之一，其中的元素迁移、分散和累积受到地域特征的制约，既表现出垂向和区域的结构性，又具有时空上的渐变性[1]。而土壤质地作为土壤的重要物理属性，在母质、气候、地形、人类活动等因素的影响下，也会在空间上呈现出特定的规律和结构性。研究土壤质地的空间分布规律，对指导土壤改良、灌溉排水管理、生态农业区划以及水土资源合理利用具有重要的现实意义，进而为灌区农业可持续发展奠定基础[1-2]。

土壤质地的空间变异性分析和插值方法有很多，其中基于变异函数理论的克里金法应用最为广泛，但是克里金法往往会产生平滑效应，即高估较小值却低估较大值。杨雨亭等[3]研究发现，克里金平滑效应会导致结果无法真实反映土壤水分空间分布的局部特征，李江等[4]在地下水位的克里金插值研究中发现平滑效应对极高值与极低值点的准确预测产生了较大的影响。

决定土壤质地类型的颗粒组成属于典型的成分数据，在插值中需额外满足各成分非负且和为常数 (1或100%)的约束条件。AITCHISON[5]提出了对数比转换的方法用于解决成分数据的闭合问题，后来有学者又进行了大量改进和研究[6-7]。对数比转换方法有很多种类，主要包括加和对数比(ALR)转换[5]、中心对数比(CLR)转换[5]、等距对数比(ILR)转换[6]和对称对数比(SLR)转换[7]。已有研究表明，与直接对原始数据插值相比，对于经过对数比转换的土壤颗粒组成进行插值的结果更加合理，精度也更高[8-11]。WAN等[8]研究表明ALR转换对克里金插值结果的平滑性产生了一定影响。但目前不同转换方法对克里金插值平滑性的影响分析研究较少。

此外，关于非成分数据克里金平滑效应的专门处理方法也有很多研究。随机模拟是重现区域化变量空间结构的方法，可以避免平滑效应，但是无法保证局部估计精度且结果不唯一[12-13]。OLEA等[13]提出的补偿克里金法全局最优性不如随机模拟，局部精度亦低于传统的克里金估计。JOURNEL等[14]的后处理方法较好解决了平滑效应问题，但也降低了局部估计精度。YAMAMOTO[15-16]提出的后处理方法会导致插值表面光滑性降低，而且仍局限在克里金法的理论体系内。段建军等[17]提出的极差平滑率和标准差平滑率等定量指标较好地评估了克里金的平滑效应，并且提出了简单易行的一元二次回归模型校正方法，但也存在特征点少、模型稳定性不够的缺点。目前，在土质插值中考虑组分数据克里金插值平滑效应及其校正的研究较少。

BP神经网络是一种应用最广泛的人工神经网络模型，结构简单，适用性强，具有较强的非线性函数逼近能力，在数据预测、样本分类等研究中均有较好的精度及应用价值[18-21]。在克里金插值中验证点的残差受到周围观测点及其克里金权重的影响，这也是产生平滑效应的原因，而决定克里金权重的变异函数一般是非线性模型，因此基于BP模型寻找残差与邻近点的关系就有了可能。

本文以内蒙古河套灌区的土壤质地为研究对象，基于普通克里金法进行空间插值，分析评估不同的对数比转换方法对克里金插值平滑效应和插值精度的影响，进一步建立基于BP神经网络的后处理模型，以期能够较好地改善克里金插值结果的平滑效应，提升插值精度，并得到较为合理的研究区土壤质地空间分布。

1 材料与方法

1.1 研究区概况

河套灌区位于内蒙古自治区西部的巴彦淖尔市境内(40.1°～41.4° N，106.1°～109.4° E)，是我国干旱区的最大灌区，也是亚洲最大的一首制灌区，东西长约500 km，南北宽20～90 km，灌区占地 1.21×106hm2，灌溉面积约7.3×105hm2(图1)。

河套灌区地处典型的中温带大陆性季风气候区，蒸发强烈，降水稀少。年平均气温6～8℃，自东向西升高；平均相对湿度40%～50%；年日照时数为3 100～3 300 h；年平均降水量为150～200 mm，自东向西递减；20 cm蒸发皿年蒸发量 1 900～2 300 mm。河套灌区种植结构十分复杂，作物呈插花式、细碎化分布。其中，春玉米、向日葵和春小麦是河套灌区的主要作物，占总种植面积的85%以上[22]。

河套灌区是由于黄河携带大量泥沙在狼山以南的陷落地带冲刷堆积而形成的冲积平原，土地肥沃，整体上地势西南高、东北低，高程在1 000～1 090 m之间，该地形特征为自流式引水灌溉提供了天然条件。灌区土壤类型主要以盐渍化浅色草甸土、盐土和灌淤土为主，质地偏砂，有机质含量约1%，含盐量较高。

1.2 土样采集与颗粒组成测定

本研究采用网格法和随机法相结合的方式进行点位设计，使得采样点不仅能均匀覆盖全灌区，而且采样点的间距也有大有小，共计采样298个(图1)。土样采集时间为2018年5月、2019年9月和2021年5月，采样点主要分布于农田内，利用手持GPS进行定位确定采样点的经纬度，采集表层土 0～20 cm 内的混合土样作为待测样品进行室内分析。

采用筛分法和比重计法测定土壤颗粒组成，根据美国农业部土壤质地分类法，利用土壤黏粒(Clay)、粉粒(Silt)和砂粒(Sand)的含量(质量分数)，将土壤质地类型分为黏土、砂质黏土、粉质黏土、粉质黏壤土、黏壤土、砂质黏壤土、壤土、粉壤土、粉土、砂质壤土、壤质砂土、砂土。由于灌区内土质不会在短期内发生变化，因此3年的采样数据一起处理和统计分析，通过R语言编程以及GS+ 9.0软件进行。

1.3 研究方法

1.3.1成分数据的对数比转换方法

AITCHISON[5]最早提出成分数据的对数比转换方法，用以解决成分数据在插值过程中的闭合效应和统计分析问题，后续又经过不同学者改进与发展。目前，对数比转换方法主要包括加和对数比(ALR)、中心对数比(CLR)、等距对数比(ILR)和对称对数比(SLR)4种转换方法，使用时均是先将各颗粒组分通过转换公式进行变换，然后对变换后的数据进行插值等操作，最后采用转回公式将结果转换为原始的成分数据形式，这样的变换过程能够保证插值后的土壤颗粒各组分总和为100%，满足定和、非负等约束。

加和对数比(ALR)转换公式和转回公式为[5]

yi=ln(zi/zD) (i=1,2,…,D-1)

(1)

其中

(2)

式中zi——第i种颗粒的质量分数(依次是黏粒、粉粒和砂粒)

yi——转换后的颗粒i质量分数

yj——转换后的颗粒j质量分数

D——颗粒组分种类数量，取3

中心对数比(CLR)转换公式和转回公式为[5]

(3)

(4)

等距对数比(ILR)转换公式和转回公式为[6]

(5)

其中

(6)

对称对数比(SLR)转换公式和转回公式为[7]

(7)

其中

(i=1, 2, …,D)

(8)

式中δi——样点中第i种颗粒最小质量分数(除0外)的1/2

δj——样点中第j种颗粒最小质量分数(除0外)的1/2

1.3.2普通克里金法

克里金法是地质统计学的主要内容之一。普通克里金(Ordinary Kriging, OK)是最早被提出和系统研究的克里金法，它实质上是一个线性估计系统，基本原理是利用半变异函数模型来拟合经验半变异函数，通过无偏估计和最优估计条件建立克里金线性方程式，求解各样本线性权重，最后用各样本及其权重表示未知点估计值[23]。

在二阶平稳假设条件下，对土壤颗粒组分的普通克里金估计公式为

(9)

式中Z(x0)——位置x0处的土壤颗粒组分估计值

Z(xi)——已知位置xi处的土壤颗粒组分观测值

λi——权重系数

n——用于估计的已知样点个数

在无偏和最优的约束条件下，可得克里金方程组

(10)

式中μ——拉格朗日乘数

γ——变异函数

通过式(9)、(10)求解，即可得到权重系数λ，进而求得估计值。插值结果的精度采用交叉验证法评价，即对任意一个采样点，利用除该点之外的采样数据进行插值得到该点的插值结果，其与实测值的差值作为误差，然后计算1.3.5节的精度评价指标。

1.3.3BP神经网络平滑性校正模型

BP神经网络是一种信号向前传递、误差反向传播的有监督人工神经网络，适用于非线性分类和回归问题，由输入层、隐含层和输出层组成。

输入层的特征变量为插值点周围的观测值序列。首先确定待插值点的位置，然后通过邻近法寻找距离插值点最近的n个观测点，这里的n与克里金插值时所用的插值点数量n保持一致，并将这n个点从近到远排序；在交叉验证中，每个采样点依次进行类似操作，通过汇总，可以得n个向量，每个向量是由距离插值点远近排序相同的观测点组成，其元素个数为采样点总数。比如对于不同插值点，对应距离最近的点组成第1个特征，第2近的点组成第2个特征，依次类推，可以得到n个特征向量。

其次确定输出变量。在交叉验证中，获得每个点的克里金插值结果后，计算插值残差，以此作为神经网络模型的输出变量。

根据交叉验证的结果，得到训练数据集，经过反复调整参数得到效果较好的BP网络模型。对于某个位置的插值结果，将插值点周围观测值特征序列输入模型，即可估算该插值点的残差，然后结合插值结果，得到校正后的最终插值结果。

1.3.4平滑性指标

克里金插值的平滑效应是指插值后原来的高值被低估，而原来的低值被高估，呈现一种趋中性，因此本研究采用极差平滑率、标准差平滑率指标来衡量平滑效应[17]，计算式为

(11)

(12)

式中CR——极差平滑率

CS——标准差平滑率

Ro——采样点观测值极差

So——采样点观测值标准差

RI——采样点估计值极差

SI——采样点估计值标准差

其中，CR和CS越大，说明平滑性越严重。

1.3.5精度评价指标

本研究在克里金插值中选择合适的变异函数模型，需要通过交叉验证法进行插值精度评估；其次在插值后构建BP神经网络平滑性校正模型时，需要评估模型精度。采用平均绝对误差(Mean absolute error, MAE)和均方根误差(Root mean squared error, RMSE)作为精度指标来评价模型，通常两个指标的值越小，模型的效果越好。

2 结果与分析

2.1 描述性统计分析

图2为土壤实测样本颗粒组成的小提琴分布图。砂粒、粉粒和黏粒表现出不同的分布特点。其中黏粒含量平均值为15.3%，与中位数接近；粉粒含量平均值为40.5%，低于相应的中位数；砂粒含量平均值为44.2%，高于其中位数。从数据的分布形状来看，黏粒分布的对称性更好，粉粒向高值一侧偏斜，而砂粒向低值一侧偏斜。黏粒含量相对较低，分布集中，粉粒和砂粒含量整体较高，说明土壤黏粒不是该地区主要的控制性组分。另外粉粒和砂粒的分布范围较广，几乎在0～100%内均存在，说明其变异性也较大。从极端值分布来看，黏粒中相对来说存在较多，在高值和低值区均存在，粉粒和砂粒的极端值相对较少。极端值的存在会影响插值结果的平滑性，一般来说，极端值越多平滑性越严重。在实际插值中，往往会将这些点视作异常值剔除，但是灌区中的确有沙地存在，为了反映客观事实和对插值平滑性的探索，本研究保留这些极端值。

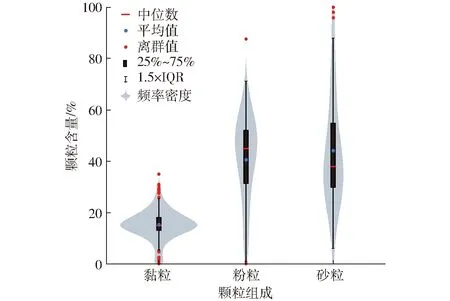
图2 土壤实测样本颗粒组成分布Fig.2 Distribution of soil particle-size fractions for observed samples

图3 为对数比转换前后的土壤组分数据的正态性分布。在转换之前，粉粒相对来说更接近正态性，黏粒由于两边极端值较多而偏离正态曲线较多，砂粒中高值部分偏离了正态曲线。原始土壤组分数据经过不同的对数比转换后，在正态性上表现各有差异。ALR转换后的第1成分ALR1除了两端少数点外的大部分点都在正态曲线上，第2成分ALR2除了较大的极端值偏离较多外，也基本都在正态曲线上。CLR和SLR转换后的3个成分均各自对应于原始数据的黏粒、粉粒和砂粒组分，CLR1和SLR1表现类似，都是低值部分偏离较多，其他大部分点都接近标准线；CLR2和SLR2也是低值部分偏离较多；而CLR3和SLR3则是高值部分偏离较多，主要是因为原始数据中黏粒和粉粒均存在极端的低值，而砂粒相应存在极端的高值。对于ILR转换，其中组分ILR1与ALR1类似，大部分值在标准线附近，而ILR2与ALR2不同，主要是极端的低值部分偏离了标准线。

图3 原始样本及对数比转换后数据的正态分位图Fig.3 Normal quantile-quantile plots for original and logratio transformed data

为了进一步说明正态性的变化，通过Kolmogorov- Smirnov(KS)检验得到原始样本和不同转换后的数据的p值结果，如表1所示。在剔除极端值之前，对数比转换前后差别不大，远不能满足正态假设；但剔除极端值以后，经过对数比转换的数据p值更接近甚至大于0.05，正态性明显得到了改善。综上可知，原始数据中由于存在离群值的情况，很难完全符合标准正态分布，即使经过对数比转换也很难使所有数据都靠近标准线，但是可以使除极端值之外的大部分数据更加接近正态分布。

表1 原始样本及不同对数比转换后数据的KS检验的p值结果Tab.1 p values by KS test for original and logratio transformed data

2.2 基于原始数据的OK插值

首先使用普通克里金法直接对原始的土壤颗粒组分数据进行插值计算，然后对交叉验证结果进行分析和评估。如图4所示，对原始数据直接使用OK插值的结果具有较明显的平滑性，平滑率基本都在0.3以上，其中粉粒的平滑性最大，极差平滑率和标准差平滑率均在0.4以上，黏粒和砂粒的平滑性较为接近，极差平滑率在0.3左右，标准差平滑率在0.35左右。

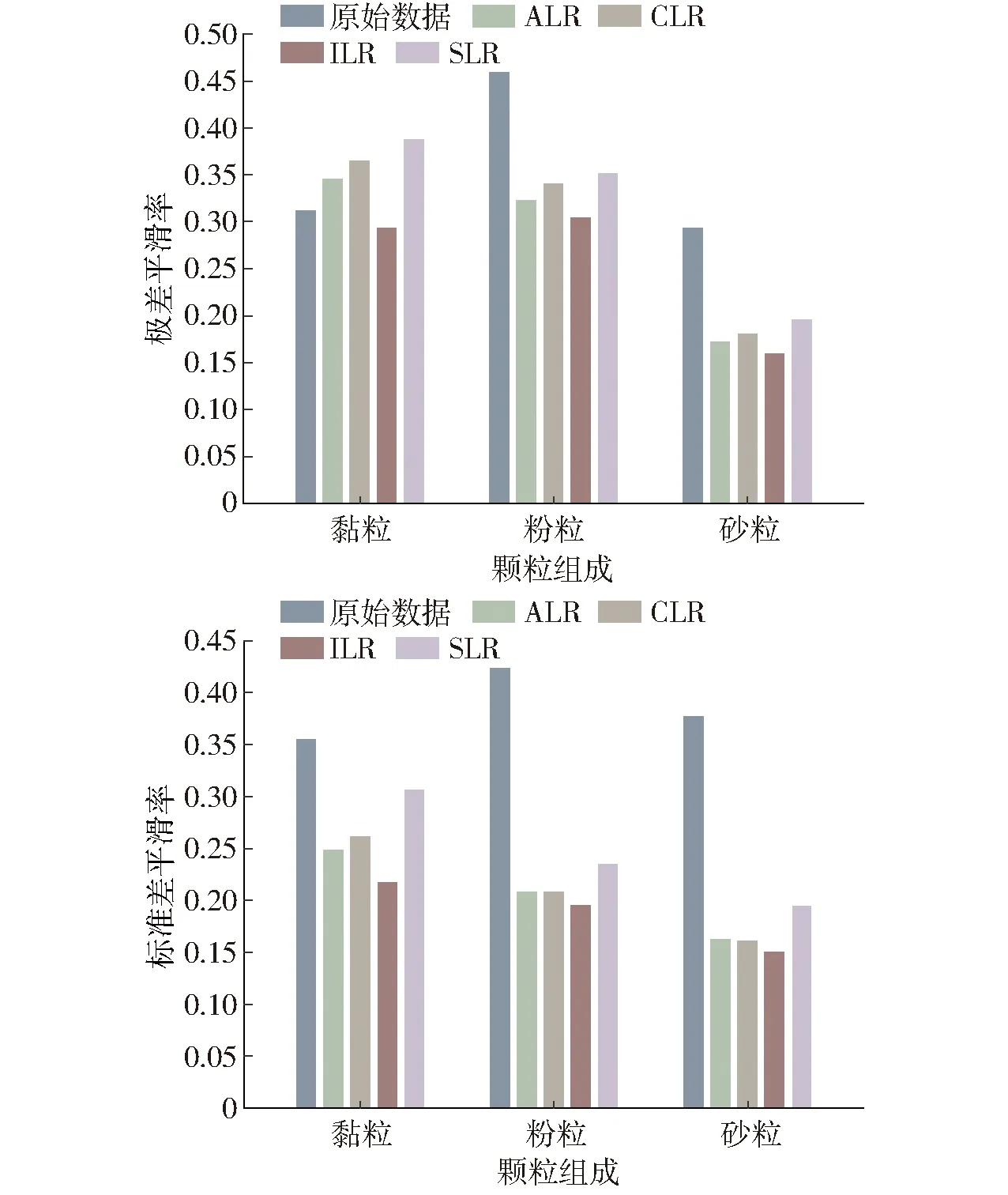
图4 土壤颗粒组成原始数据及对数比转换数据的插值平滑率Fig.4 Smoothing rates for interpolation of original soil particle size fractions and logratio transformed data

图5为原始数据的OK插值精度评价结果。从图5可以看出，不同组分的插值精度具有明显差异，其中黏粒的插值精度最高，平均绝对误差和均方根误差分别为4.4%和5.6%。插值精度最差的是砂粒，两个指标均大于12%，而粉粒精度介于黏粒和砂粒之间，平均绝对误差为10.5%，均方根误差为12.9%。

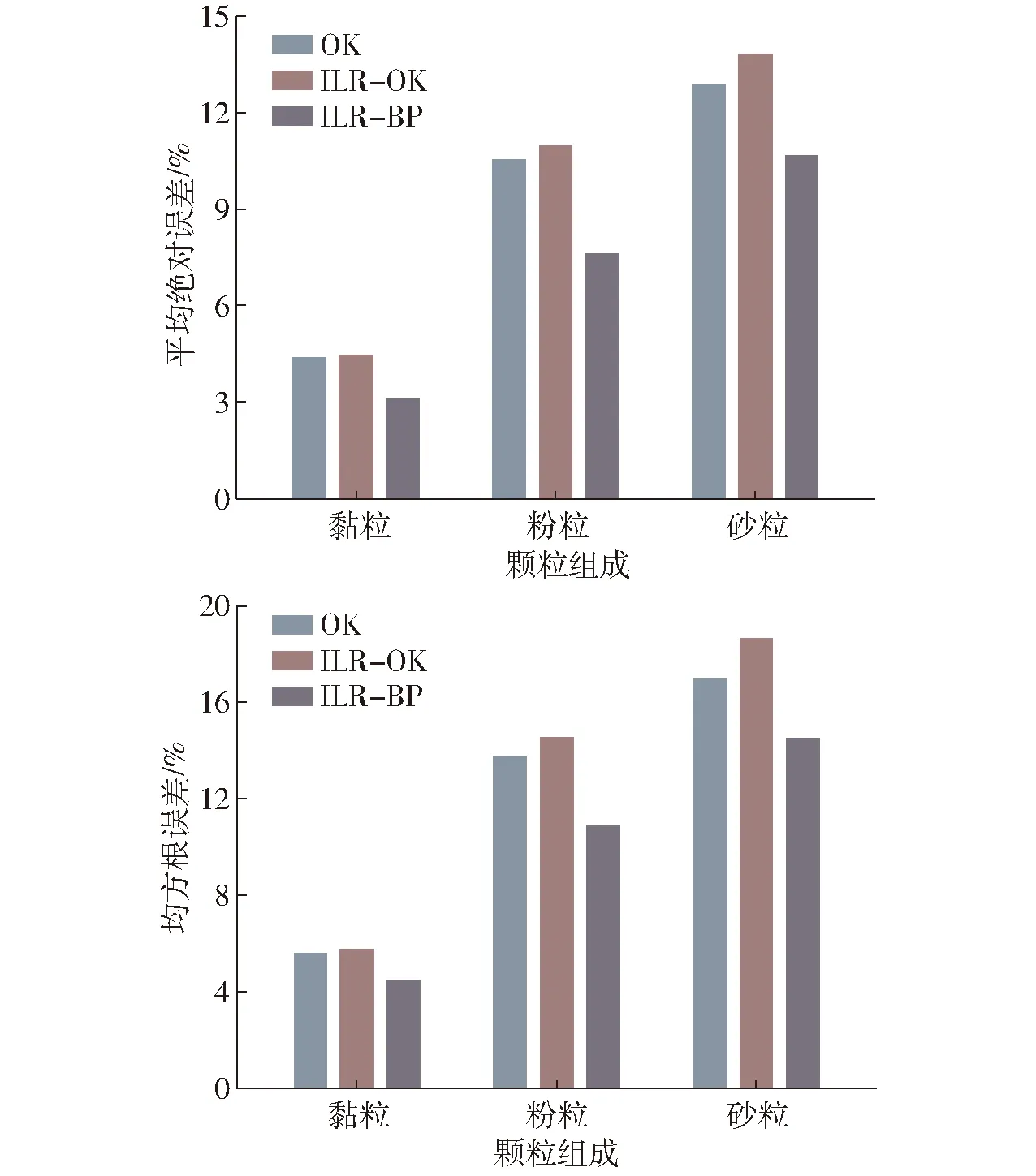
图5 不同方法插值的交叉验证精度Fig.5 Comparisons of accuracy indexes of cross-validation for different methods

2.3 基于不同对数比转换的插值平滑性评估

原始组分数据经过4种不同的对数比转换后，再用普通克里金插值，然后再使用转回公式得到最终结果，通过交叉验证结果评估插值的平滑性(图4)。与原始数据的直接插值结果不同，经过对数比转换后的插值结果中，砂粒的平滑性得到了明显改善，极差平滑率由0.3降低到0.2以下，标准差平滑率也由0.38下降到0.15左右。黏粒的插值平滑性改善效果相对较差，其中极差平滑率甚至大于原始数据，在3个组分中平滑性最严重。粉粒则位于两者之间，其极差平滑率由0.45下降到0.3左右，标准差平滑率也由0.43下降到0.25以下。

不同的转换方法对平滑性的影响程度也有所不同。从极差平滑率来看，SLR转换结果的平滑性最大，ALR和CLR相差不大，而ILR转换结果的平滑性最小，其中黏粒和粉粒分别为0.29和0.30，砂粒仅为0.16。对标准差平滑率而言，规律类似，ILR具有最小的平滑性，黏粒、粉粒和砂粒的标准差平滑率依次为0.22、0.20和0.15。总体而言，ILR转换方法在普通克里金插值中对平滑性的改善效果最好。与直接使用普通克里金插值的结果相比, 黏粒、粉粒和砂粒的极差平滑率分别减小5.8%、33.8%和45.6%，标准差平滑率分别减小38.6%、53.9%和60.2%。另外从图5中可以看出，基于ILR转换数据的插值(ILR-OK)对各颗粒组分的插值精度影响不大，甚至比直接使用OK还略差，其主要原因是对数比转换中考虑了组分数据的特性，相当于增加了OK插值的约束条件。

2.4 基于ILR转换和BP神经网络的平滑效应校正模型(ILR-BP)

与基于原始数据的普通克里金插值相比，对ILR转换后的数据插值可以改善平滑性，但还依然存在较大的平滑率，尤其是黏粒和粉粒仍具有接近0.3的极差平滑率，因此需要进一步修正以降低平滑性。在ILR-OK的交叉验证结果中，将目标点的插值残差作为训练目标，同时将目标点插值与周围邻近点观测值的残差构成的特征向量作为输入，通过构建BP神经网络模型拟合两者之间的关系，不断调试参数，将具有较好训练效果的模型作为最终的残差预测模型。

图6为3种颗粒组分的残差预测BP模型的拟合效果。由图6可见，不同组分的残差分布不同，黏粒的残差最小，粉粒次之，而砂粒的残差较大。另外，散点基本均匀分布在1∶1线两边，黏粒的拟合效果相对较好，平均绝对误差和均方根误差分别为3.24%和4.61%；粉粒和砂粒由于原始的残差比较大，变异性强，因此整体拟合效果不如黏粒好。大部分散点主要集中在0值附近，说明大部分插值点的平滑性不明显，而少数分布在两端的点是影响平滑性的主要因素，也是决定平滑性修正效果的关键点。总体可见，残差预测模型的拟合效果在可以接受的范围内，尤其是对于较大的残差，即平滑性严重的样点，有较强的拟合能力。

图6 基于ILR-BP的残差预测模型评估结果Fig.6 Evaluation results of residual prediction model based on ILR-BP

基于残差预测模型的预测结果，对ILR转换数据的交叉验证结果进行校正。根据平滑性校正前后观测值与交叉验证结果的对比(图7)可以发现，校正后的极差平滑率均为0，并且标准差平滑率也接近0(0.03 ～ 0.07)，说明平滑性得到了很大改善，相比只使用ILR转换，平滑性得到了进一步明显的削弱。其中粉粒的平滑性效果改善最大，从原来的0.4以上直接减小为0，而黏粒和砂粒的标准差平滑率比粉粒稍大，均为0.07，但总体上平滑性也已很小。从散点分布来看，校正后的散点比校正前分布更加离散，但是更加均匀地分布在1∶1线的两边，靠近均值的点变化不大，高值区和低值区的点则均有向1∶1线靠拢的趋势，更说明了校正模型对极端值平滑性的改善效果。从平滑性校正前后的插值精度对比(图5)可以发现，经过ILR-BP模型校正后各组分的插值精度均有所提高。黏粒的平均绝对误差和均方根误差分别减小29.4%和19.8%；粉粒的精度提高也较为明显，两个指标分别减小27.6%和21.0%；砂粒的精度提升效果不如黏粒和粉粒，两个指标分别减小17.1%和14.6%。因此，校正后的结果在平滑性得到极大改善的同时，还能保证插值精度有所提升。

图7 平滑性校正前后观测值与交叉验证结果对比Fig.7 Comparisons between observations and cross-validation results before and after smoothing correction

由于土壤颗粒各组分是单独进行插值，平滑性会直接体现在各组分自身上，但土壤质地类型是黏粒、粉粒和砂粒的含量共同决定的，因而各组分的插值平滑性会进一步影响到土质类型的预测结果。为了进一步比较ILR-BP模型校正后与校正前的土质类型变化情况，根据美国制标准，通过土壤质地三角来展示原始样本数据以及插值平滑性校正前后的交叉验证结果，如图8所示。由图8a可知，原始样本数据中，共有7种土质，主要为壤质砂土、砂质壤土、壤土和粉壤土，另外还有少量的砂土、黏壤土和粉质黏壤土。直接经过OK插值的交叉验证结果却只有4种主要的土质(图8b)，正是因为插值的平滑效应，各组分的结果都向中部集中，使得原始样本中存在的3种土质消失了。为了避免这种现象的发生，需要进行平滑性校正，校正后的土质分布与原始样本高度一致(图8c)，首先是分布的离散程度，相比校正前的趋中性，校正后明显更加分散；其次土质类型也包括了原始样本中的所有7种土质，但是也出现了个别原始样本中没有的砂质黏壤土，主要是因为原始样本中存在靠近砂质黏壤土与砂质壤土界限的一部分样点，分类的不确定性大。因此，通过土质类型的对比，可以看出ILR-BP模型校正后的结果能更准确地描述原始样本中的土壤质地类型。

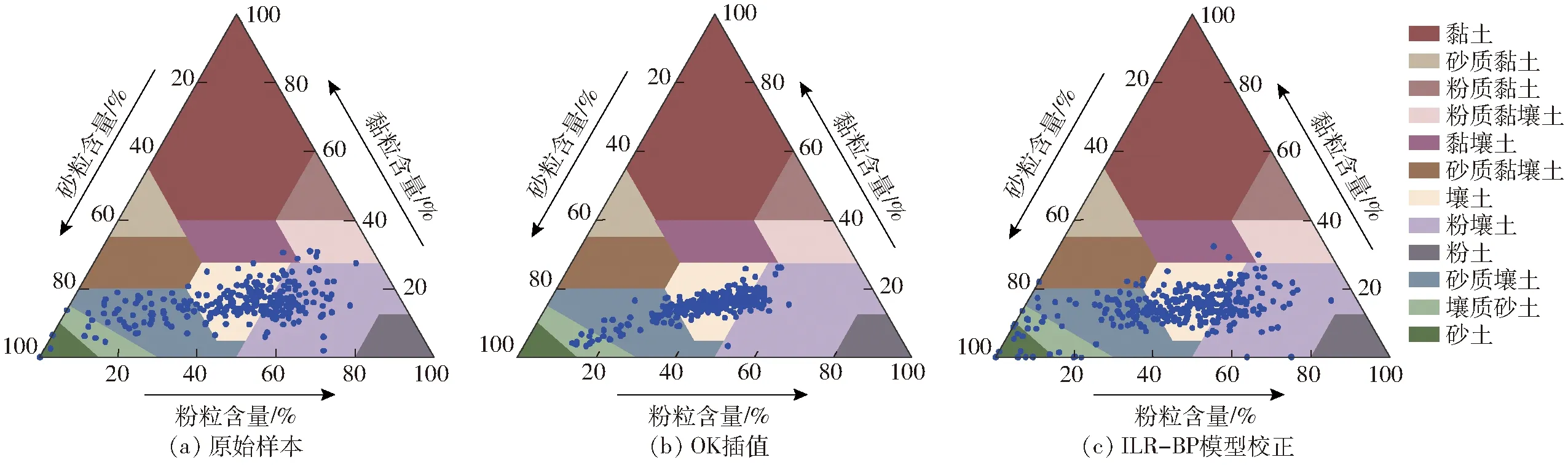
图8 原始样本点及平滑性校正前后交叉验证结果的土质类型对比Fig.8 Comparisons of soil texture types for original samples and cross-validation results before and after smoothing correction

2.5土壤颗粒组成及质地空间分布基于ILR-BP模型可以对研究区内表层土壤颗粒组分的空间分布插值结果进行校正，如图9所示，图中各组分的范围是根据原始样本数据设定的。图9a为直接用OK插值后没有经过校正的结果，由于平滑效应，插值的预测值都在相应阈值内，而且基本无法显示出极端值的分布区域。图9b为经过平滑性校正后的空间分布，黏粒在灌区中部和西部含量较低，在这两个地方也确实存在黏粒含量几乎为0的测量样本，但是校正前的黏粒分布中几乎不能体现这一特点。另外灌区大部分地区黏粒含量在15%～20%，东部存在零散的地区偏高。粉粒的分布特点与黏粒类似，校正后的分布更加精细，局部特征更明显，尤其是存在极端低值的样本区域，大部分地区的粉粒含量在40%左右。对于砂粒而言，几乎与黏粒和粉粒的分布趋势相反，主要是因为成分数据的定和约束，砂粒含量在灌区西部和中部偏南的部分地区较高，这也与实际采样的结果一致。校正前的砂粒分布虽然也有此规律，但是原本的极端高值由于平滑效应而消失了，另外灌区东部存在砂粒含量较低的区域，大部分区域的砂粒含量在50%以下。总体而言，校正后的颗粒含量空间分布更加明晰准确，局部变异特征更加明显，更能反映采样数据的空间特征。基于土壤颗粒组分的空间分布，根据美国制标准，可以计算出相应的土质类型的空间分布，如图10所示。由图10a可以看出，主要有4种土质类型，即壤质砂土、砂质壤土、壤土和粉壤土，与原始样本的主要土质一致，但是没有反映出其余3种分布较少的土质类型的采样点特征，这正是由于平滑效应造成的结果。由图10b可知，灌区中部和西部主要是偏砂性的土壤，与校正前相比，还显示出了砂土的分布特征；壤土和粉壤土的面积最广，其中壤土主要集中分布在中西部、东北部和东南部，粉壤土主要分布在北部和南部靠近黄河的地区；除此之外，灌区内还存在零星分布的黏壤土和粉质黏壤土，这与采样点的土质类型基本一致。因此，经过平滑性校正后，土质的空间分布既能保证整体规律不变，又能反映更加真实的土质类型，呈现出更加明显的交错分布特征。

图9 平滑性校正前后土壤颗粒组成空间分布Fig.9 Spatial distributions of soil particle size fractions before and after smoothing correction

图10 平滑性校正前后土壤质地类型空间分布Fig.10 Spatial distributions of soil texture types before and after smoothing correction

在河套灌区，平均2～3年农田就会深耕一次，土壤经过上下的频繁翻动，可以认为作物根系区的土壤质地较为均匀，研究中采用表层0～20 cm土样具有代表性。根据ILR-BP模型校正之后的河套灌区各土质类型面积及占比情况，如表2所示，壤土和粉壤土的面积占比分别达到41.7%和27.3%，二者覆盖了2/3以上的灌区面积；砂质壤土次之，占比15.8%；砂土和壤质砂土不到10%；其余3种占比很小，共占1.4%左右。

表2 河套灌区各土壤质地类型面积及相应占比Tab.2 Areas and proportions of different soil texture types in Hetao Irrigation District

3 讨论

3.1 插值平滑效应与插值精度的关系

克里金插值中的平滑效应主要指高值低估和低值高估现象，为了定量表示，采用段建军等[17]提出的极差平滑率和标准差平滑率，从数据离散程度的变化反映平滑效应。插值精度是用来衡量插值结果整体准确度的指标，本研究中采用使用广泛的平均绝对误差和均方根误差来表示。平滑效应和插值精度之间存在一定联系，但不完全同步变化。

以形式较为简单的极差平滑率和平均绝对误差为例。其中极差平滑率主要是通过最大值和最小值的插值前后变化来计算，本质上反映了极端值的插值精度。平均绝对误差的计算是把所有样本点的插值误差都考虑在内，当然也包括极端值的误差。从这个角度看，极差平滑率是构成平均绝对误差的一部分。如果经过插值方法改进，极端值的插值误差虽然减小但幅度不大，而其他样本点的总误差增大，那么就有可能导致平滑效应减小而插值精度却没有提高的现象，如ILR-OK的插值结果所示。但如果极端值的插值误差减小的同时，其他样本点的误差也都不同程度地减小，那么平滑效应和插值精度就同时得到改善，如ILR-BP的插值结果所示。因此平滑率并不能完全决定插值精度，两者也不存在绝对的同步变化关系。

3.2 对数比转换对平滑效应的影响

对数比转换是处理成分数据常用的方式。由于成分数据具有定和、非负的基本特点，在插值中为了保持这种性质，需要使用对数比转换公式。此外，转换前后数据的分布和数据维度会有所改变。根据前人的研究[9,24]，对数比转换一般能够改善原始数据的正态性，图3也说明了这一结论。从图3可以看到，除个别极端值之外的数据，正态性确实得到了改善，但是同时也说明了对数比转换不能很好处理存在极端值的情况。

对数比转换还会影响插值结果的平滑性。根据图4，经过对数比转换后，土壤颗粒含量插值结果的平滑性大都得到了一定的改善(黏粒的极差平滑率除外)。可能是因为转换后的数据具有更好的正态性，使得插值结果的统计特征与原始数据更加一致，极差平滑率和标准差平滑率也更小。同时不同的对数比转换对平滑性影响的程度也不同，但差别不大。从本研究可以看出，ALR和CLR表现相似，主要是因为两者的转换形式类似，SLR也是基于ALR和CLR的原理进行改进，表现却更差一些，但是ILR对平滑性的改善效果非常明显，可能是因为ILR转换方法符合Aitchison空间中同度量的转换，是直接对数据处理的方法[6]。

3.3 ILR-BP模型校正的作用及与其他校正方法对比

克里金插值的平滑效应主要原因包括：首先是克里金插值的本质是局部线性加权平均，插值结果会更靠近局部平均值，因此使用的邻近点个数会影响插值结果。邻近点个数越多，结果就会更加稳定地趋向平均值，平滑效应就越明显，所以不宜使用过多邻近点，但是邻近点又不能太少，否则插值结果不能反映空间变异规律。其次与地统计理论有关，克里金插值的算法基础是变异函数，它能反映区域化变量空间变异的规律，但在实际计算中，是通过拟合经验变异函数散点得到理论的变异函数模型，而且模型往往是非线性的。在变异函数拟合过程中，会抵消原始数据中的一部分变异性和随机性，使得插值系数会具有一定的平滑性，最终导致插值结果的平滑性。但总体上还是遵循地理学第一定律，即越近的点对插值结果影响越大。事实上，平滑效应是克里金法的一种固有特点，李超[25]研究指出，应当客观看待平滑性，要针对具体的研究目的进行分析。

由此可见，邻近点值的大小和距离插值点的远近是影响插值结果平滑性的主要因素。所以本研究提出使用按一定空间距离排列的邻近点序列作为输入特征，通过BP神经网络模型训练，建立邻近点特征与插值结果残差的关系，并结合对数比转换处理，建立了ILR-BP校正模型。ILR转换主要是为了预处理成分数据，在插值后再使用转回公式，这个非线性过程改变了数据的统计特征，导致极端值的插值预测比原始数据直接插值好，一定程度上削弱了平滑性。进一步削弱平滑性主要依靠BP神经网络模型的后处理方法，由于其直接基于残差规律修正插值结果，大部分样本点插值误差都会不同程度减小，尤其是极端值插值结果得到明显改善，因此平滑性得到了明显削弱，同时插值精度也有所提升。

ILR-BP模型有以下特点：首先，理论简单，不需要复杂的统计学理论，只需要找到合适的特征值预测残差的分布即可。而YAMAMOTO[15]提出的方法是基于标准差数来校正，需要通过一系列的统计计算，稍显复杂。其次，ILR-BP模型校正效果明显，在保证插值精度的基础上，能在很大程度上改善插值的平滑性。YAMAMOTO[15]校正方法中还需要使用克里金法去插值标准差数，从本质上来讲还是局限在克里金法之中；段建军等[17]使用一元二次回归模型来模拟残差的规律，虽然较为简单，但是特征点较少，模型不一定能反映真实的规律；而本文的ILR-BP模型方法是基于机器学习，拟合能力更强。最后，ILR-BP模型方法也存在一定的局限性，即对采样点的个数有要求，如果采样点太少，可能无法训练出较稳定的模型。

3.4 河套灌区土质空间分布的影响因素分析

河套灌区是由于黄河冲积作用形成的冲积平原，因此其中的母质大部分来自于上游的泥沙，整体上土质偏砂性。灌区西部位于河流上游，由于河流运动的分选和沉积作用，上游的颗粒偏粗，而中下游的颗粒更细，因此砂粒主要分布在灌区西部，而中东部更多的是粉粒和黏粒。但是由于人类活动和其他因素的影响，局部也会有异常现象，比如中部存在砂粒集中的区域，这在河套灌区也较为常见，灌区中零散分布着大小不一的沙丘，这正是黄河冲积作用的见证，后来由于人类耕作活动使得土壤得到了一定的改良。

4 结论

(1)基于对数比转换的普通克里金法对平滑效应有一定的改善作用，不同转换方法的改善程度也不相同。ALR和CLR的效果一般，作用类似，SLR的改善作用最小，ILR的效果最好，改善后的黏粒、粉粒和砂粒的标准差平滑率依次为0.22、0.20和0.15。

(2)基于ILR转换和BP神经网络相结合的校正模型(ILR-BP)能够较好地削弱克里金插值中的平滑效应。校正后的土壤组分交叉验证结果的极差平滑率为0，标准差平滑率为0.03～0.07，同时平均绝对误差和均方根误差都有一定的下降，这说明平滑性得到校正的同时，插值精度也有所提高。

(3)校正后的土壤颗粒组成和质地类型的空间分布更加精细，局部特征更加明显，并且能够很好地还原样本的特征，在极端值的表现上更加符合实际。河套灌区中部和西部主要是偏砂性土壤，壤土主要集中分布在中西部、东北部和东南部，粉壤土主要分布在北部和南部接近黄河的地区。

(4)基于ILR-BP的普通克里金法不但能够解决成分数据空间插值问题，同时能够削弱插值的平滑效应，得到较为真实的区域土壤质地分布，为河套灌区的水盐运移研究和水土资源规划提供了基础资料。