考虑输出刚度不确定性的柔顺机构拓扑优化设计

占金青 李翼丰 朱本亮 刘 敏

(1.华东交通大学载运工具与装备教育部重点实验室， 南昌 330013；2.华南理工大学广东省精密装备与制造技术重点实验室， 广州 510641)

0 引言

柔顺机构具有一体化加工、无噪声、无需润滑和高精度等优点[1-3]，广泛用于微纳操作、精密加工、仿生机器人和微机电系统(Micro-electro-mechanical system, MEMS)等领域[4-7]。柔顺机构的设计方法主要有伪刚体模型法和拓扑优化方法。与伪刚体模型法相比，柔顺机构拓扑优化设计无需从已知的刚性机构出发，在给定设计域、输入及输出作用等条件下获得最优的柔顺机构拓扑构型，并且使其某种性能达到最优[8-10]。然而，目前大多数柔顺机构拓扑优化设计研究都是在确定性条件下进行的。

实际上，柔顺机构在设计、制造及运行中存在大量的误差和不确定性，忽略不确定性因素可能导致设计的机构构型不一定最优，且容易导致机构运动精度降低。KOGISO等[11]基于均匀化方法建立了考虑作用载荷方向不确定性的柔顺机构稳健性拓扑优化模型，获得的机构输出位移标准差更小，具有更好的稳健性。罗阳军等[12]考虑载荷及材料属性不确定性因素，提出一种考虑不确定性的柔顺机构稳健性拓扑优化设计方法。LAZAROV等[13]采用随机配置方法量化材料和几何不确定性，进行柔顺机构稳健性拓扑优化设计研究。WANG等[14]引入田口质量损失函数的期望作为优化目标，建立了基于运动误差的柔顺机构稳健性拓扑优化模型，并通过实验验证了稳健性设计结果的有效性。ZHAN等[15]基于非概率有界场模型进行考虑材料不确性的无类铰链柔顺机构稳健性拓扑优化设计，分析了有界不确定场的相关长度对机构拓扑构型的影响。上述研究主要集中研究载荷、材料和几何尺寸不确定性因素。

通常，柔顺机构拓扑优化设计需要在输出端施加虚拟输出弹簧刚度用来模拟被操作对象的刚度，优化设计结果很大程度上取决于输出刚度，被操作对象的刚度存在不确定性，这会对设计的柔顺机构运行精度产生影响，因此需降低机构性能对输出刚度不确定性的敏感程度。CARDOSO等[16]考虑输出刚度不确定性进行柔顺机构稳健性拓扑优化设计，但是采用蒙特卡罗模拟方法计算机构输出位移的期望和标准差，需要利用大量样本进行不确定性分析，导致优化计算效率低。

本文提出一种新的考虑输出刚度不确定性的柔顺机构稳健性拓扑优化设计方法。采用区间模型描述输出刚度的不确定性，不确定输出刚度被视为均匀分布的随机变量，通过高斯随机变量的无记忆非线性变换获得其均匀分布；采用多项式混沌展开式结合Smolyak稀疏网格积分法计算随机响应统计矩；以机构输出位移的期望值最大化和标准差最小化为目标函数，以机构结构体积为约束，建立考虑输出刚度不确定性的柔顺机构稳健性拓扑优化模型；采用移动渐近线法更新设计变量。

1 输出刚度不确定性描述

区间模型[17]只需要指定不确定变量的上界和下界，可以相对容易地确定和描述不确定性的边界；本文采用区间模型描述输出刚度的不确定性，将不确定输出刚度kout视为均匀分布区间变量，其可表示为

kout∈kI=[kL,kU]

(1)

式中kI——区间集

kL——区间下界

kU——区间上界

区间均值与幅值分别记为

(2)

式中k0——输出刚度均值

kc——输出刚度幅值

输出刚度不确定区间变量可等效转换为均值与随机项之和，即

kout=k0+kcδ

(3)

式中δ——均匀分布随机变量，取[-1,1]

区间模型的均匀分布随机变量δ可由高斯分布随机变量通过无记忆非线性变换[18]得到

(4)

ξ——高斯分布随机变量

Φξ——标准高斯变量的累积分布函数

2 柔顺机构稳健性拓扑优化模型

为了降低柔顺机构运动精度对输出刚度不确定性的敏感程度，采用改进的固体各向同性材料惩罚模型[19-20]，以机构的输出位移期望值最大化和输出位移标准差最小化为目标函数，以机构体积为约束，建立考虑输出刚度不确定性的柔顺机构稳健性拓扑优化模型

(5)

其中

式中ρ——单元密度向量列阵

ρe——第e个单元的密度

ve——充满材料的单元体积

λ——加权系数

u0——机构输出位移

μ——机构输出位移期望值

σ——机构输出位移标准差

F——输入端作用的载荷列阵

U——载荷F作用产生的节点位移列阵

V——优化后体积

V0——初始设计域体积

f*——允许的材料体积比

N——有限单元数目

K——整体刚度矩阵

Ke——单元刚度矩阵

Kin——整体输入刚度矩阵

Kout——整体输出刚度矩阵

3 随机响应求解

不确定性输出刚度区间变量由标准高斯随机变量ξ表示，机构的输出响应U(ξ)可采用PCE[21-22]表示为

(6)

式中yi——多项式展开系数

ψi(ξ)——正交多项式基函数

正交多项式基函数满足

(7)

式中δij——Kronecker delta函数

E[·]——期望运算符

根据Askey策略[23]，对于不同的随机变量分布类型，采用相应的正交多项式基函数，其中对于高斯分布随机变量ξi，采用对应的Hermite多项式Hαi(ξi)(αi对应随机变量ξi的多项式阶数)，对多个随机参数，ψi可表示为

(8)

i=(α1,α2，…,αs)

式中s——随机变量数量

i——索引元组

多项式混沌展开的总阶数p计算式为

p=|i|=α1+α2+…+αs

(9)

数值计算中，一般将多项式(6)截断为指定阶数，即

(10)

根据给定的随机变量数量s和多项式阶数p，截断后PCE系数的项数表示为

(11)

多项式混沌展开式(6)中系数yi的表达是不确定性系统响应求解的关键，其表示为

(12)

(13)

式中nq——总积分点数

ω(q)——积分点对应的权值

U(ξ(q))——特定积分点下的系统响应，可通过有限元分析求解获得

基于Smolyak算法的稀疏网格积分法[25]依据随机变量的不同分布情况采用不同积分规则的稀疏网格类型，能够有效地减少计算成本并保证精度。本文采用Kronrod-Patterson(KP)规则获得稀疏网格积分点。输出位移期望值和标准差分别表示为

(14)

(15)

4 灵敏度分析

采用基于梯度的优化算法(Method of moving asymptotes，MMA)[26]求解柔顺机构稳健性拓扑优化问题，需要求解优化目标函数和约束灵敏度信息。

机构输出位移的期望值对单元密度ρe的灵敏度可表示为

(16)

机构输出位移的标准差对单元密度ρe的灵敏度可求解为

(17)

其中

(18)

式(18)的每个特定积分点ξ(q)(q=1,2,…,nq)的确定性输出位移相对于单元密度的灵敏度∂u0(ρ,ξ(q))/∂ρe，可由机构输出位移u0对单元密度求导得到

(19)

(20)

5 数值算例

通过夹持器与咬合机构来验证提出的设计方法的有效性。在两个算例中，设计域尺寸L×L为 120 μm×120 μm，厚度t为3 μm，实体材料弹性模量E0为180 GPa，空洞材料弹性模量Emin为1.8×10-7GPa，泊松比μ为0.3，允许体积比f*为0.25，最小过滤半径rmin为2.5倍单元尺寸；采用四阶PCE和基于五级KP规则的Smolyak稀疏网格积分法计算随机响应。

5.1 夹持器设计

夹持器机构设计域、边界条件和载荷作用如图1所示，设计域左边的上侧和下侧固定，设计域右边正方形空洞尺寸为30 μm×30 μm，载荷F作用在左边中点，大小为10 mN，输入刚度kin为1 000 μN/μm，输出刚度均值k0为100 μN/μm。由于夹持器设计域是对称的，取一半设计域进行设计，设计域离散为 7 200 个平面四边形单元。

图1 夹持器设计域Fig.1 Design domain of gripper

为了验证提出的设计方法有效性，首先进行夹持器确定性拓扑优化设计，获得的夹持器拓扑构型如图2所示，其输出位移的期望值和标准差分别为13.831 μm和0.770 μm。考虑不确定输出刚度幅值kc为25 μN/μm和加权系数λ为10条件下进行夹持器稳健性拓扑优化设计，获得的夹持器拓扑构型如图3所示，其输出位移的期望值和标准差分别为10.597 μm和0.261 μm。与确定性优化结果相比，稳健性拓扑优化获得的夹持器构型存在明显的差异，右侧区域的支撑杆件布局发生变化，并且其尺寸变大；夹持器的输出位移期望值有所减小，但是输出位移标准差减少66.2%；表明稳健性拓扑优化设计能够有效地降低夹持器对输出刚度不确定性因素的敏感程度，验证了提出的考虑输出刚度不确定性的柔顺机构稳健性拓扑优化设计方法的有效性。

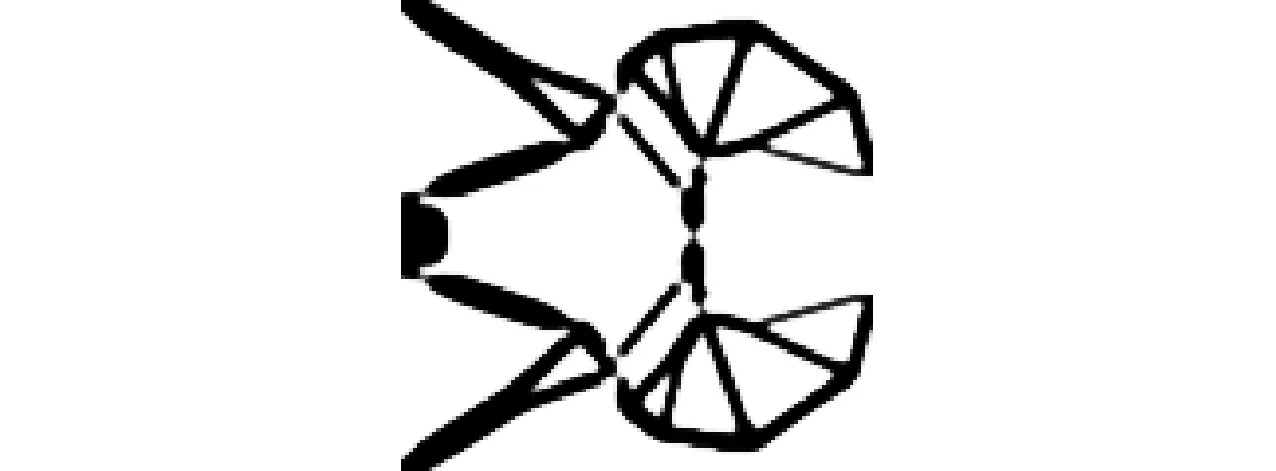
图2 夹持器确定性拓扑优化结果Fig.2 Gripper obtained by deterministic topology optimization

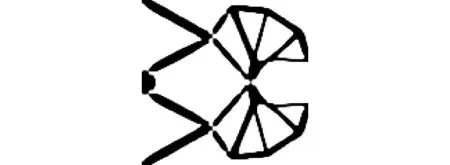
图3 夹持器稳健性拓扑优化结果Fig.3 Gripper obtained by robust topology optimization

为了研究不同的加权系数对拓扑优化结果影响，考虑不确定输出刚度幅值kc为25 μN/μm条件下，取加权系数λ分别为1、5、15进行夹持器稳健性设计，拓扑优化结果如图4和表1所示。由此可见，随着加权系数λ的增大，获得的夹持器构型有所不同，右侧区域的支撑杆件尺寸变大；夹持器的输出位移的期望值随之减小，输出位移标准差也越小。表明加权系数λ越大，可以获得更加稳健的夹持器，但夹持器的输出位移期望值越小。

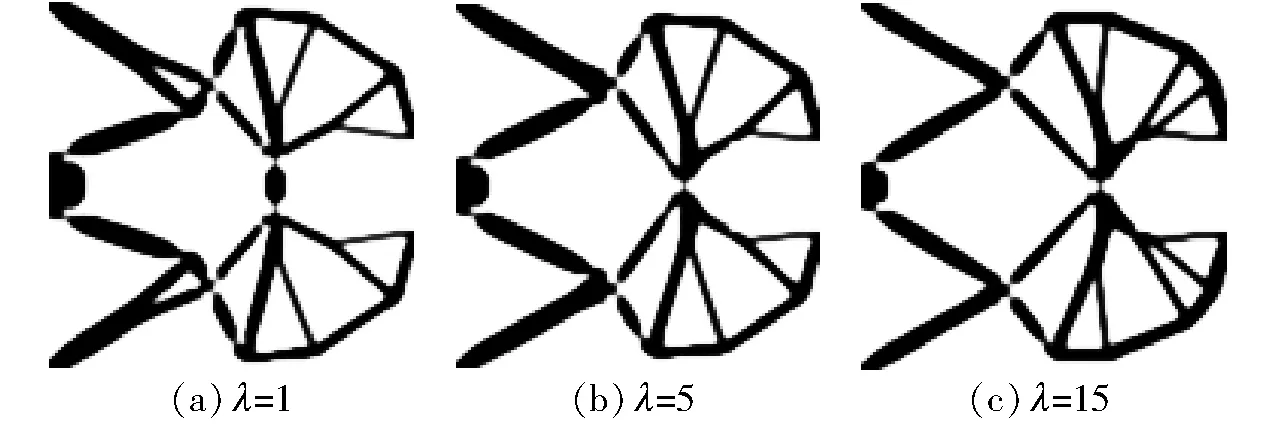
图4 不同加权系数λ的稳健性拓扑优化获得的夹持器构型Fig.4 Grippers obtained by results for robust topology optimization with different weighting factor λ

表1 不同加权系数λ的夹持器稳健性优化结果Tab.1 Results for robust topology optimization of gripper with different weighting factor λ

考虑加权系数λ为5条件下，采用不确定输出刚度幅值kc分别为20、30、35 μN/μm的条件下进行夹持器稳健性拓扑设计，拓扑优化结果如图5和表2所示。随着不确定输出刚度幅值增大，获得的夹持器拓扑构型差异不大；输出位移期望值随之减小，输出位移标准差有所增大。稳健性拓扑优化设计获得的夹持器输出位移期望值与标准差均比确定性拓扑优化更小。上述结果表明提出柔顺机构稳健性设计方法能够有效地降低夹持器对输出刚度不确定性因素的敏感程度，但夹持器输出位移期望值有所减小。

图5 不同输出刚度幅值kc的稳健性拓扑优化获得的夹持器构型Fig.5 Grippers obtained by results for robust topology optimization with different amplitude kc

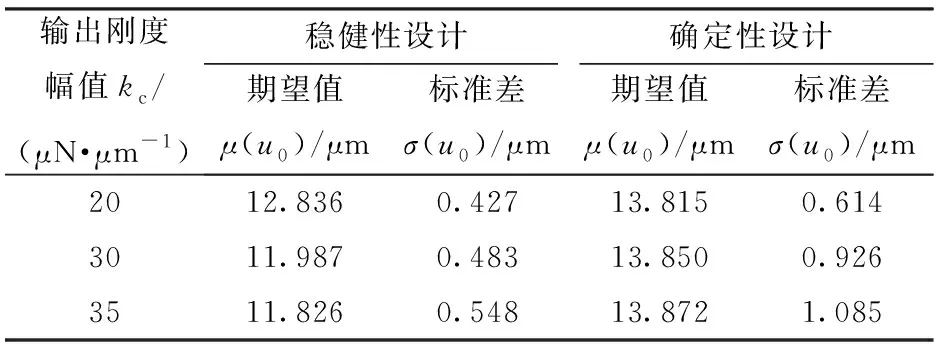
表2 不同输出刚度幅值kc的夹持器确定性与稳健性拓扑优化结果Tab.2 Results for deterministic and robust topology optimization of gripper with different amplitude kc

5.2 咬合机构设计

咬合机构设计域、边界条件和载荷作用如图6所示，设计域左边的上、下两端固定，载荷F作用在右边的上、下两端，大小为20 mN，输入刚度kin为1 000 μN/μm，输出刚度均值k0为1 000 N/m。由于设计域是对称的，同样采用一半设计域进行设计，设计域离散为7 200个平面四边形单元。

图6 咬合机构设计域Fig.6 Design domain of crunching mechanism

同样地，分别进行咬合机构确定性和稳健性(kc=250 μN/μm，λ=10)拓扑优化设计，获得的咬合机构拓扑构型分别如图7、8所示，输出位移期望值分别为9.318、7.509 μm，输出位移标准差分别为0.714、0.276 μm。与确定性拓扑优化结果相比，稳健性拓扑优化获得的咬合机构构型存在明显差异、更加复杂，存在更多支撑杆件，这样可以更好地承受输出刚度扰动的影响，具有更好的稳健性。稳健性拓扑优化获得的咬合机构输出位移期望值和标准差均比确定性结果小，同样表明稳健性拓扑优化设计能够有效地降低咬合机构对输出刚度不确定性因素的敏感程度，验证了提出的考虑输出刚度不确定性的柔顺机构拓扑优化设计方法的有效性。

图7 咬合机构确定性拓扑优化结果Fig.7 Crunching mechanism obtained by deterministic topology optimization

图8 咬合机构稳健性拓扑优化结果Fig.8 Crunching mechanism obtained by robust topology optimization

考虑不确定输出刚度幅值kc=250 μN/μm条件下，取加权系数λ分别为1、5、15进行咬合机构稳健性拓扑优化设计，优化结果如图9和表3所示。由图9可见，随着加权系数λ增大，稳健性拓扑优化获得的咬合机构拓扑构型更加复杂，出现更多支撑杆件，承受输出刚度扰动的影响能力更强，具有更好的稳健性。由表3可知，随着加权系数λ增大，获得的咬合机构的输出位移期望值与标准差均随之减小。这也说明随着加权系数λ越大，可以获得更加稳健的咬合机构，但是输出位移期望值越小。

图9 不同加权系数λ的稳健性拓扑优化获得的咬合机构Fig.9 Crunching mechanisms obtained by robust topology optimization with different weighting factor λ

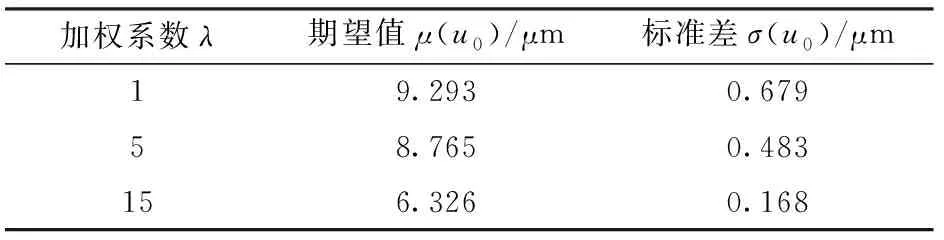
表3 不同加权系数λ的咬合机构稳健性优化结果Tab.3 Results for robust topology optimization of crunching mechanism with different weighting factor λ

当加权系数λ为5时，考虑不确定输出刚度幅值kc分别为200、300、350 μN/μm进行咬合机构拓扑优化设计，拓扑优化结果如图10和表4所示。随着不确定输出刚度幅值增大，获得的咬合机构拓扑构型差异不大；咬合机构输出位移的期望值随之减小，输出位移的标准差有所增大。稳健性拓扑优化设计获得的咬合机构输出位移期望值与标准差均比确定性拓扑优化更小。表明提出柔顺机构稳健性设计方法能够有效地降低咬合机构对输出刚度不确定性因素的敏感程度，但是咬合机构的输出位移期望值有所减小。

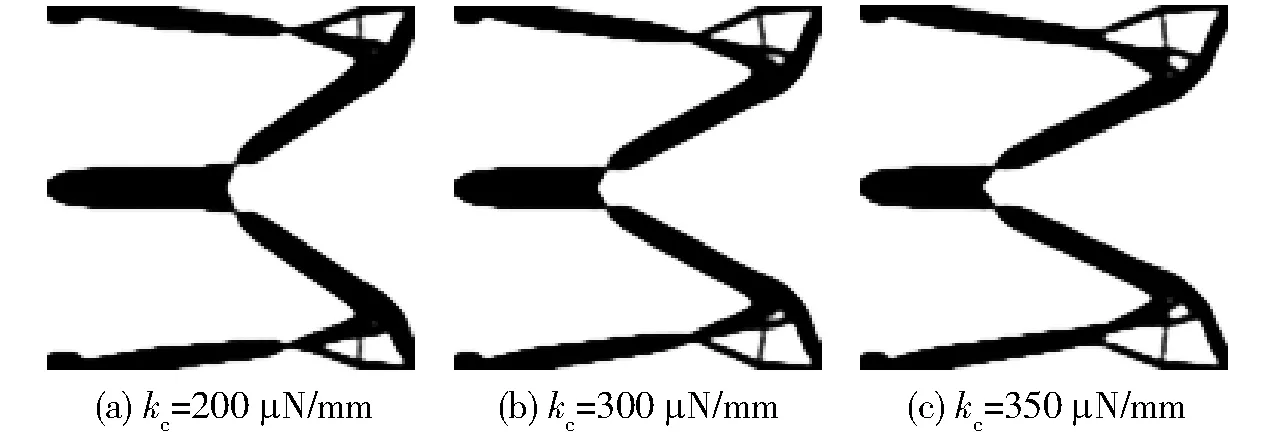
图10 不同输出刚度幅值kc的稳健性拓扑优化获得的咬合机构构型Fig.10 Crunching mechanisms obtained by robust topology optimization with different amplitude kc

表4 不同输出刚度幅值kc的咬合机构确定性与稳健性优化结果Tab.4 Results for deterministic and robust topology optimization of crunching mechanism with different amplitude kc

6 结论

(1)为了降低机构性能对输出刚度不确定因素的敏感程度，采用区间模型描述输出刚度的不确定性，利用多项式混沌展开式和Smolyak稀疏网格积分法计算随机响应统计矩，以机构输出位移期望值的最大化和加权标准差的最小化为目标函数，提出一种考虑输出刚度不确定的柔顺机构稳健性拓扑优化方法。

(2)与确定性拓扑优化结果相比，稳健性拓扑优化获得的柔顺机构拓扑构型存在明显差异，机构的输出位移标准差减小，能够有效地降低机构对输出刚度不确定性因素的敏感程度，机构具有更好的稳健性，但是输出位移的期望值也有所减小。

(3)随着加权系数增大，稳健性拓扑优化获得的柔顺机构拓扑构型有所不同，机构输出位移的期望值与标准差随之减小，机构具有更好的稳健性。随着不确定输出刚度幅值增大，获得的柔顺机构拓扑构型差异不大，机构的输出位移标准差随之增大，并且输出位移期望值有所减小。