神经网络化简非多项式混合布尔算术表达式
刘彬彬,凤维杰,郑启龙,2,李 京
1(中国科学技术大学 计算机科学与技术学院,合肥 230026) 2(中国科学技术大学 安徽省高性能计算重点实验室,合肥 230026)
1 引 言
混合布尔算术(Mixed Boolean-Arithmetic,MBA)表达式[1,2]是指混合使用位运算符(如&,|,~等)和算术运算符(如+,-,*等)的表达式,如表达式3*(x&y)-y+2.相关文献[1,3]给出了混合布尔算术表达式的形式化定义,并将其分类为多项式和非多项式混合布尔算术表达式.另外,文献[1,3]提出多种方法来产生大量的混合布尔算术恒等式,如x=(x^y)+y-2*(~x&y).混合布尔算术表达式主要被用于软件混淆领域中,其是一种先进的软件混淆技术[4,5].混合布尔算术混淆技术可以将一个简单的表达式替换为一个复杂的但语义等价的表达式,如将x替换为(x^y)+y-2*(~x&y).因此,混合布尔算术混淆技术已经被多个学术界和工业界项目所采用[4,6,7-9].
混合布尔算术表达式的大范围应用促使研究人员探索如何反混淆混合布尔算术表达式,也就是化简混合布尔算术表达式.相关实验结果表明,目前已有的计算数学软件都不能处理混合布尔算术表达式[10,11].故研究人员提出了多种不同的化简方法,包括:语义等价变换方法[4,11],bit-blasting[12],模式匹配[13],程序合成技术[14],和基于深度学习的解决方案[15,16].虽然这些方法都能够化简特定形式的混合布尔算术表达式,但是相关实验结果表明[3,11],这些方法都不能有效处理非多项式混合布尔算术表达式.并且,文献[3]提出使用安全性更高的非多项式混合布尔算术表达式替代已有的多项式混合布尔算术表达式.因此,化简非多项式混合布尔算术表达式是一个极具挑战的任务.
为了化简非多项式混合布尔算术表达式,本文提出一种字符串到字符串的解决方案NeuSim,该解决方案基于神经网络模型来自动化学习和化解表达式.首先,在序列到序列和图序列神经网络架构的基础上,本文构造并实现了NeuSim.其次,针对相关数据集匮乏的问题,本文收集并生成一个大规模的数据集,该数据集包含1000000条多种形式的非多项式混合布尔算术表达式.最后,本文在生成的数据集上训练NeuSim,并在测试集上进行测试.相关实验结果表明,与已有工具的化简结果相比,NeuSim的化简正确率是已有解决方案的8倍,并且化简时间可以忽略不计(低于0.01秒).
本文的主要贡献总结如下:
1)本文提出一种端到端的解决方案NeuSim来化简非多项式混合布尔算术表达式,并且构建了相应的序列到序列和图序列神经网络模型.本文是首个应用神经网络化简非多项式混合布尔算术表达式的研究.
2)本文构建了业界第一个大规模的非多项式多混合布尔算术表达式数据集,其包括各种形式的非多项式混合布尔算术表达式及其等价的简单表达式.
3)大规模的实验结果表明,相较于已有的化简方法,NeuSim的化简正确率至少提高7倍,并且化简时间至少快1个数量级.此外,与本研究相关的资源(代码,数据集,和神经网络模型)可在如下网址公开获取:https://github.com/nhpcc502/NeuSim.
本文接下来的组织如下:第2部分介绍混合布尔算术表达式的相关背景知识;第3部分介绍本文提出的字符串到字符串的解决方案NeuSim;第4部分介绍相关实验结果及其分析;第5部分是本文总结.
2 相关工作
2.1 混合布尔算术表达式
文献[1,2]提出了混合布尔算术表达式的概念,其是指混合使用位运算符(如&,|,~等)和算术运算符(如+,-,*等)的表达式,定义1给出了多项式混合布尔算术表达式的形式化定义.如果一个混合布尔算术表达式不符合定义1,那么它将属于非多项式混合布尔算术表达式[1,3],这说明多项式和非多项式混合布尔算术表达式之间是补集的关系.
定义1.一个多项式混合布尔算术表达式如公式(1)所示,其中ai为整数常量,ei,j(x1,…,xt)为n-bit变量x1,…,xt的位运算表达式.
∑i∈Iai(∏j∈Jiei,j(x1,…,xt))
(1)
文献[1]设计了一种基于真值表的矩阵乘法方法,并用其来产生大量的多项式混合布尔算术恒等式.在已有的混合布尔算术恒等式的基础上,文献[3]提出多种形式化的方法来产生众多的多项式和非多项式混合布尔算术恒等式.混合布尔算术恒等式主要被用于软件混淆(software obfuscation)领域[4,5],是一种先进的软件混淆技术.混合布尔算术混淆技术可以将一个简单的表达式等价替换为一个复杂的等价表达式,并用其来复杂化程序代码.
由于混合布尔算术混淆技术的理论正确性和使用成本低廉,该技术已被多个学术界和工业界项目所采纳[4,6-9],其也可被用于算法优化中[17].另一方面,研究人员开始探索如何反混淆混合布尔算术表达式,也就是理解复杂的混合布尔算术表达式并还原出一种语义等价的简单形式.由相关文献可知[10,11],常用的SMT求解器和符号计算软件都不能化简混合布尔算术表达式.因此,研究人员提出多种不同的解决方案来处理混合布尔算术表达式,包括:基于语义等价变换的技术[4,11],bit-blasting[12],模式匹配[13],程序合成技术[14],和基于深度学习的方法[15,16].这些化简方法都可以处理特定类型的混合布尔算术表达式,其中基于语义等价变换的方法是最有效的,它们能够高效处理多项式混合布尔算术表达式.但是,在面对非多项式混合布尔算术表达式时,已有的方法都表现出了明显的不足[3,11].并且,文献[3]提出使用安全性更高的非多项式混合布尔算术表达式等价替换已有的多项式混合布尔算术表达式.
2.2 神经网络处理数学表达式
文献[15]探索了如何使用神经网络化简多项式混合布尔算术表达式,其提供了一个大规模的线性混合布尔算术表达式(多项式混合布尔算术表达式的特例)数据集,并且用该数据集训练相关的序列到序列神经网络模型,实验结果表明其在线性混合布尔算术表达式上取得了较好的效果.文献[16]注意到已有的基于序列到序列模型在解决数学表达式时存在的潜在不足,进而提出使用图序列神经网络来处理数学表达式.相关实验表明,图序列神经网络相较于序列到序列模型,在处理有关数学表达式任务时具有更高的正确率.
此外,已有多个研究工作使用神经网络模型来处理数学问题.相关文献[18,19]使用序列到序列的模型来处理数学表达式,如表达式重写和数学表达式问答;文献[20]使用树神经网络来进行逻辑推理.然而,对于本文所研究的非多项式混合布尔算术表达式化简问题,目前业界尚无相关工作.
3 化简非多项式混合布尔算术表达式
化简非多项式混合布尔算术表达式的目标是给出一个简单的等价表达式,本节将详细介绍一种字符串到字符串的解决方案NeuSim,该方案使用神经网络来学习和化简非多项式混合布尔算术表达式.为了横向对比目前业界最为经典的各类数学表达式计算模型,本文构建并实现了两类神经网络模型:序列到序列架构的模型和图序列机构的模型.由于目前业界缺乏非多项式混合布尔算术表达式数据集,本文在相关文献的基础上,生成了一个大规模的非多项式混合布尔算术表达式数据集.
3.1 神经网络模型结构
本文基于编码器-解码器架构[21]来实现NeuSim,其结构主要分为两部分:负责从输入表达式中学习隐藏模式的编码器,以及根据学到的知识预测表达式化简结果的解码器,模型结构如图1所示.NeuSim的输入是一个以序列形式呈现的、长度可动态变化的非多项式混合布尔算术表达式.编码器通过学习输入数据的特征,并输出一个固定长度的隐藏状态向量来表示学习到的表达式特征.解码器是由循环神经网络组成,通过预先设定的字典,NeuSim可以将解码器的输出重构成一个简单的表达式,也就是对应的非多项式混合布尔算术表达式的化简结果.

图1 NeuSim模型结构示意图Fig.1 Architecture of NeuSim
为了全面比较不同的神经网络模型之间的性能差异,本文采用两类不同的神经网络架构来构建NeuSim的编码器:序列到序列的模型和图序列的模型.其中,构建基于长短期记忆网络LSTM[22],门控循环单元GRU[23],和注意力机制[24]的序列到序列的模型;同时,构建基于图卷积架构[25]的图序列网络模型.在序列到序列的模型中,NeuSim直接将输入的长度可变的非多项式混合布尔算术表达式输出给编码器.在图序列模型中,NeuSim首先需要对输入的非多项式混合布尔算术表达式进行预处理(将输入的表达式转换成有向无环图(DAG图)),然后将DAG图输出给图卷积编码器.
3.1.1 序列到序列神经网络模型
混合布尔算术表达式多以字符串的形式进行保存和处理,故本文首先研究如何构造一个基于序列到序列架构的NeuSim.在序列到序列的模型中,编码器和解码器都由循环神经网络组成,其输入输出也是由字符组成的、长度可变的字符串.为了对比各种不同的序列到序列神经网络模型对NeuSim性能的影响,本研究采用3种广泛使用的循环神经网络(长短期记忆网络LSTM[22],门控循环单元GRU[23],和注意力机制BERT[24])作为NeuSim编码器和解码器的核心构件,接下来将详细介绍这3种神经网络模型的结构.
本文构建的第1个模型是基于长短期记忆网络LSTM[22]的NeuSim.LSTM是自然语言处理领域最为经典的神经网络模型之一,它可以较好地解决长输入中相同字符相隔较远导致模型无法捕获长期依赖的问题.首先,在模型的编码器中构造一个嵌入层作为输入的非多项式混合布尔算术表达式接收器,该嵌入层通过独热编码的方式将输入的表达式向量化.在嵌入层之后,编码器构造了激活函数为tanh的4层LSTM层.通过时间依赖的迭代学习,编码器可以从输入的表达式中学习到相应地隐藏模式,并将这些隐式信息抽象化为一个固定大小的隐藏向量.在解码器中,其首先构造一个嵌入层,该嵌入层以隐藏向量作为输入,并将其输出给一个由4层LSTM组成的神经网络.最后,解码器的输出向量通过一个全连接层重新编码成一个新的表达式,该表达式即为对应输入表达式的化简结果.为了避免模型训练时的过拟合,本模型采用随机丢弃策略dropout,该策略可以随机丢弃神经网络中的神经元,从而避免模型产生过拟合的现象.
本文构建的第二个模型是基于门控循环单元GRU[23]的NeuSim.GRU作为循环神经网络的一种变体,它的结构更加紧凑、可学习参数量更少.具体来看,该模型的编码器首先构造一个嵌入层以独热编码方式向量化输入的非多项式混合布尔算术表达式,并用dropout策略随机丢弃该层的神经元以控制模型的拟合程度.嵌入层之后连接一个单层的GRU,其被用以学习输入表达式中各个字符之间的隐藏关系(如相同字符间的时序关系),并将这种隐藏关系抽象为隐藏向量.随后,该模型将隐藏向量输出给解码器.解码器按序分别由嵌入层、单层GRU以及全连接层构建,全连接层依据字符字典将输出的向量转换成相应的字符串,即输入表达式的化简结果.
本文构建的第3个模型是基于注意力机制[24]的NeuSim.注意力机制是目前自然语言处理领域最为有效的方法,其是一种放弃循环结构、全部采用线性层的模型策略,且能够对表达式序列中有价值的部分赋予更高的注意力(即权重),进而使模型学习到更有价值的信息.本文复现了目前业界最先进的基于注意力机制模型之一的BERT机制,并将其作为编码器的一部分.在编码器中,模型首先使用一个嵌入层将输入的非多项式混合布尔算术表达式以独热编码方式转换成向量;然后构建一个由8头注意力层和一个位置前馈层组成的基本单元,该基本单元内的各个组件之间通过正则化层进行连接;随后,将该基本单元前后连接若干次(本文使用5个基本单元).编码器的输出为一个隐藏向量,并将其输出给解码器.解码器由5个解码器基本单元组成,每个基本单元由掩码8头注意力层、8头注意力层以及位置前馈层组成,基本单元之间通过正则化层进行连接.最后,解码器的输出向量依据字符字典,通过全连接层转换成一个表达式,也即输入表达式的化简结果.
3.1.2 图序列神经网络模型
在序列到序列的模型中,以字符串形式呈现的混合布尔算术表达式不利于神经网络学习表达式中某些隐藏信息,例如在字符串序列表示中,算符的优先级需要通过添加额外的括号来明确化(如表达式x+(3*y)).为了克服序列到序列神经网络模型在处理数学表达式方面的潜在不足,目前已有研究工作应用图序列神经网络模型处理数学表达式.图序列神经网络模型通常用于输入是图输出为文本的任务中,例如视频标签生成、图像分类、蛋白质分子分类和化合物生成等任务.为了应用图序列神经网络模型处理数学表达式,首先需要将输入的表达式转换成图,如抽象语法树(AST树)和有向无环图(DAG图),该图在保留表达式相关语法语义信息的同时,可以丢弃无用的辅助信息(如括号).之后,模型对转换后的图进行处理,并且输出相应的结果表达式.
本文构建的最后一个模型是基于图序列神经网络[25]的NeuSim.首先,NeuSim需要对输入的非多项式混合布尔算术表达式进行预处理.预处理阶段通过遍历输入的表达式以生成对应的有向无环图(DAG图).基于该DAG图生成相应的特征矩阵和邻接矩阵,拼接这两类矩阵后将其送入到模型的编码器中.编码器由5层图卷积神经网络构成,后接一个全局最大池化层,且每层都使用relu作为其激活函数.编码器的输出为一个隐藏向量,该隐藏向量将输入给解码器.解码器由嵌入层、GRU以及全连接层构成,通过序列化学习生成一个输出向量,并通过字符字典得到输出向量对应的表达式,也即输入表达式的预测解.
综上所述,本文构建并实现了两类共4种不同的神经网络模型,相应的模型层数和参数大小如表1所示.

表1 神经网络模型层数和大小Table 1 Model layers and size of NeuSim
3.2 数据集
为了得到更好的化简效果,NeuSim需要大规模的数据来进行训练.然而,相关文献[3,6,17]只提供了少量非多项式混合布尔算术表达式(约1000个表达式)示例,这对于训练和测试NeuSim是明显不足的.为此,本文根据相关文献[3,6]中提出的方法来生成非多项式混合布尔算术表达式.这些方法的输入为一个简单的表达式,输出为一个复杂的等价非多项式混合布尔算术表达式.
通过进一步观察发现,文献[3,6]生成的非多项式混合布尔算术表达式具有一定的规律性和一致性[4],这些特性造成在训练Neusim时的过拟合现象.因此,为了增加非多项式混合布尔算术表达式的多样性和随机性,本文提出如下的表达式等价变换方法(用于替换的等价表达式均由文献[1]所提出的相应方法随机产生):
1)变量替换.该方法对(子)表达式中的变量进行等价变换,以期得到一个新的等价表达式,如将(x&y)变换为(((x|y)+(x&y)-y)&y).
2)常量替换.该方法将(子)表达式中的常量替换为一个等价的表达式,如将常量1替换为(x&y)-(x|y)-(~x&~y).
3)子表达式替换.该方法将表达式中的子表达式进行等价替换,如将((x|y)+(x&y))替换为x+y.
4)线性组合.该方法通过对多个表达式的线性组合,来产生一个新的等价表达式,如将表达式x+y+z=((((x|y)+(x&y))|z))+(((x^y)+2*(x&y))&z)和表达式z=(z|y)-(~z&y),线性组合为一个新的表达式x+y=((((x|y)+(x&y))|z))+(((x^y)+2*(x&y))&z)-(z|y)+(~z&y).
综上所述,本文首先通过文献[3,6]产生一个原始的非多项式混合布尔算术表达式,之后使用等价变换方法对生成的原表达式进行随机处理.从理论上说本研究可以产生无穷多个非多项式混合布尔算术表达式,但是从训练和测试NeuSim的实际出发,本文构建一个包含1000000条非多项式混合布尔算术恒等式的数据集.文献[10]指出,在实际的软件混淆场景下使用的都是3变量及其以下变量的混合布尔算术表达式.因此,数据集中包含800000个3变量及其以下变量的的非多项式混合布尔算术表达式,200000个多变量非多项式混合布尔算术表达式.
数据集中的每一条数据都是一个二元组(Eg,Ec),Eg表示一个简单的表达式,Ec表示相应等价的非多项式混合布尔算术表达式,相关表达式示例如表2所示.为了保证数据集中的每一个等式的正确性(Eg≡Ec),本文使用Z3求解器[26]对其进行验证,并且保证数据集中的每一条数据都通过了该验证.考虑到非多项式混合布尔算术表达式的复杂度和实用性,数据集共使用了10个不同的变量名.数据集中的表达式都是以字符串的形式进行保存,并且产生的表达式字符长度介于20到300之间.据本文所知,这是第一个大规模的非多项式混合布尔算术表达式数据集.
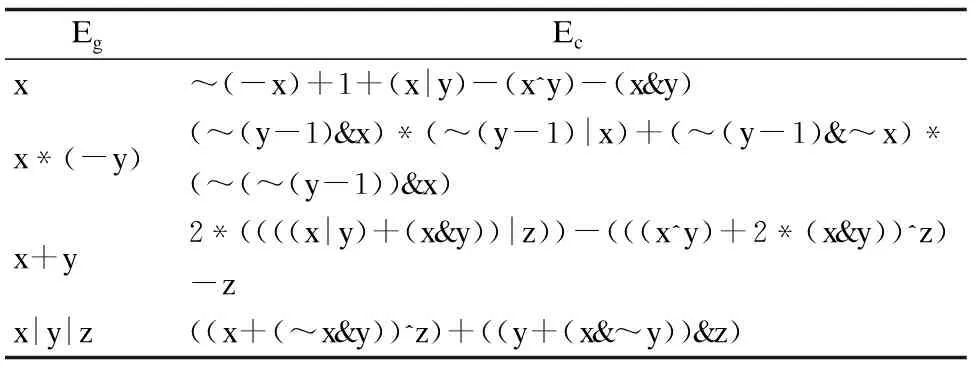
表2 数据集中的表达式示例Table 2 Samples in the dateset
4 实验与结果分析
4.1 实验设置
本文方法的实验环境为:实验操作系统为64-bit Ubuntu 20.04.4,CPU型号为Intel(R)Core(TM)i9-10980XE @ 3.00GHz,内存为64GB DDR4.本文实验使用2块NVIDIA GeForce RTX 3090 GPU训练相关的神经网络模型.本实验使用Python3编程语言,基于PyTorch框架以及PyTorch Geometric库实现本文所提出的相关神经网络模型,同时使用Python AST库实现图序列模型中的预处理操作.
针对3.1节中所描述的神经网络模型,本文使用相同的实验配置分别进行训练.首先,都对这些模型进行1000次的迭代训练,并将每次迭代的批次大小设置为128.同时在迭代过程中使用早停技术,该技术监控验证集损失下降程度来判断是否需要提前终止训练过程,进而避免资源浪费.其次,本文使用Adam优化器来学习神经网络模型中的参数,模型的初始学习率设置为1e-3,并在模型迭代的过程中使用ReduceLROnPlateau策略来动态调整学习率.最后,在模型预测阶段,本文使用Z3求解器来判断模型的输出与输入的表达式是否语义等价.
4.2 数据集设置
本实验依据概率随机抽样法从3.2节生成的数据集中随机采样100000条样本用以训练NeuSim的4个不同的神经网络模型,其中90%的数据作为模型的训练集,10%的数据作为模型的验证集.实验用的测试集是单独重新生成的,以确保每一个测试样本都不会出现在训练集中,测试集共含有10000个非多项式混合布尔算术表达式及其对应的等价简单表达式.
为了度量表达式的复杂度,本文使用以下3个指标来测量非多项式混合布尔算术表达式的复杂度,指标数值越大,也就意味着该表达式越复杂.
1)表达式中变量出现的次数.在一个表达式中,所有的变量重复出现的总次数.
2)表达式中操作符的个数.在一个表达式中,布尔操作符和算术操作符重复出现的总次数.
3)表达式长度.将一个表达式看成是一个字符串,该字符串的长度即为表达式的长度.
训练集和测试集中表达式复杂度的统计结果如表3所示,从表中均值一行可知,与简单的表达式相比,相应的非多项式混合布尔算术表达式的复杂度在几乎每一个指标上都上升一个数量级.训练集中的非多项式混合布尔算术表达式的概率分布图如图2所示.
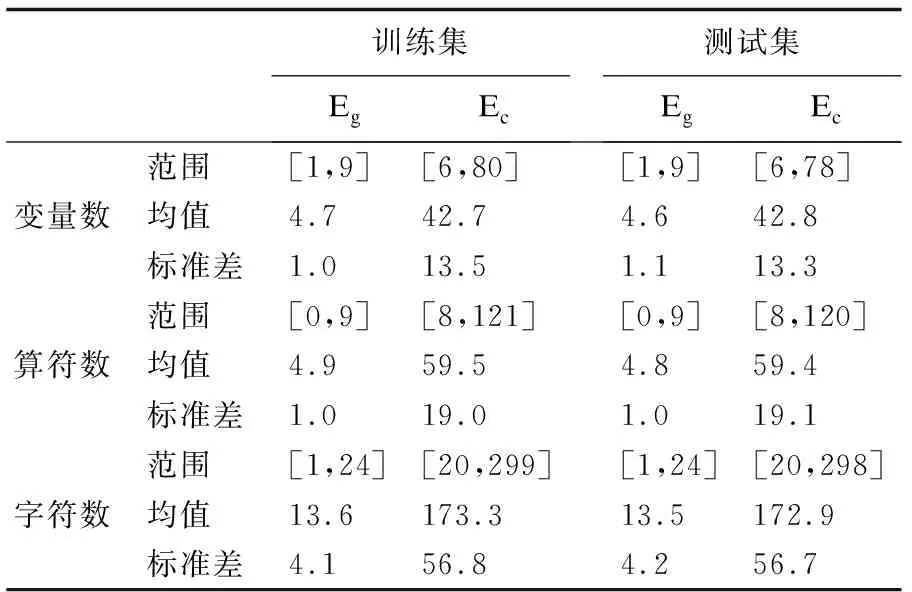
表3 数据集复杂度统计结果Table 3 Statistic of the datasets′ complexity
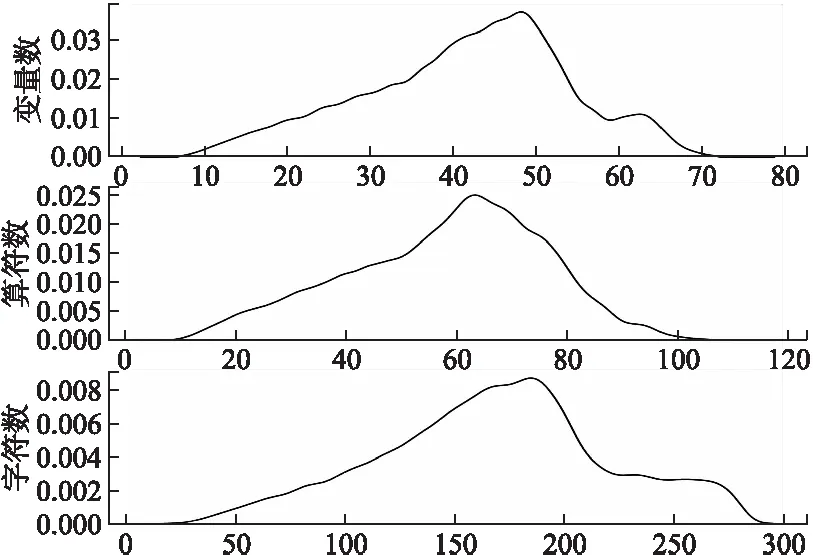
图2 训练集中复杂表达式的分布Fig.2 Distribution of the complex expression in the training dataset
从图2可知,表达式的复杂度分布基本都符合正态分布,这说明本文生成的数据集具有无偏性和随机性.
4.3 同类化简工具
从2.2节中可知,目前最先进的混合布尔算术表达式化简工具有:MBA-Blast,MBA-Solver,SSPAM,和Syntia.本研究从Github上获取了这些化简工具的源码,并在测试集中对其进行测试并记录相关实验结果.MBA-Blast可以高效化简2-变量的混合布尔算术表达式,但是MBA-Solver可以化简多变量的混合布尔算术表达式,它们都是一种语义等价的变换方法.SSPAM是一种模式匹配的化简方法,其通过一个混合布尔算术表达式规则库来进行表达式的替换和化简.Syntia是一种基于程序合成技术的化简方法,其通过学习混合布尔算术表达式的语义,产生一个语义等价但更简单的表达式.
4.4 评价标准
本文使用以下3个指标来全面测试非多项式混合布尔算术表达式化简工具的化简性能:
1)正确率:经过相关工具化简之后,化简结果与原表达式语义相等即为化简正确.本研究对化简结果通过Z3求解器进行验证,以确定其与原表达式是否语义等价,如果等价则记为Ceq.正确率的计算方法如公式(2)所示.

(2)
2)复杂度:该指标用于衡量化简后的表达式的可读性,复杂度越高意味着其可读性越低.本研究采用4.2节中的3个指标来测量化简前后表达式的复杂度.
3)求解时间:该指标衡量化简一个非多项式混合布尔算术表达式所耗费的时间.
4.5 实验结果与分析
基于以上的实验配置,本研究在训练集上分别训练NeuSim的各个模型,并通过网格搜索的方法使每个神经网络模型达到最佳性能表现.然后在同一个测试集上对各个模型的化简性能进行详细测试,并且与同类工具的化简结果进行比较.
本研究首先横向比较各种工具的化简结果正确性,所有化简结果都通过Z3求解器进行验证,验证时间阈值设置为1小时,对所有在时间阈值内无法给出结果的样本判定为无法求解,相关实验结果如表4所示.

表4 测试集上的化简结果Table 4 Simplification results on the test dataset
实验结果表明,已有的化简工具都不能有效处理非多项式混合布尔算术表达式(化简正确率都低于10%).其中,MBA-Blast和MBA-Solver的化简有效性依赖于对输入表达式中的子表达式求解:在化简表达式时,这两种方法首先需要识别表达式中可以被其处理的子表达式部分,然后通过化简子表达式来处理输入的表达式,最后处理表达式的其余部分,并给出最终的化简结果.然而,非多项式混合布尔算术表达式中的子表达式通常具有随机性和不确定性,在表达式中自动识别和正确处理相关的子表达式是极具技巧性的工作,而这导致MBA-Blast和MBA-Solver并不能很好处理非多项式混合布尔算术表达式.相比较于MBA-Blast,MBA-Solver能处理更多的表达式,这是因为MBA-Solver能够化简少量含有多变量的表达式.SSPAM在化简表达式时,其遍历该表达式与模式库中的规则是否匹配,若匹配则进行替换和化简.由于SSPAM中的模式库仅包含少量多项式混合布尔算术规则,其在匹配和替换非多项式表达式时可能会产生错误的结果.Syntia在化简表达式时首先进行表达式语义的输入-输出对采样,之后根据采样结果合成出一个语义等价的简单表达式.而非多项式混合布尔算术表达式具有形式多样性和语义复杂性的特点,这导致基于蒙特卡洛树搜索进行表达式合成的方法(Syntia)并不能有效输出语义等价的表达式.
与已有方法形成鲜明对比的是,本文所提出的字符串到字符串的解决方案NeuSim能够正确化简超过一半的非多项式混合布尔算术表达式,其中基于LSTM架构的神经网络模型的化简正确率超过66%,至少是已有工具化简正确率的8倍.同时,与现有工具的化简时间相比,NeuSim的平均化简时间为0.01秒,这比现有工具至少快1个数量级.此外,对于一个输入表达式,NeuSim的输出是一个语法正确的表达式,而不是无规则的随机字符串.从表4可知,基于GRU的模型相比于LSTM模型,其正确率稍有下降.这是因为基于GRU的NeuSim模型参数量只有基于LSTM模型的一半(表1可知),更少的模型参数量往往意味着更低的学习能力,但更少的模型参数量也表示更少的显存占用以及更短的训练时间.基于BERT的神经网络模型一般在海量数据的条件下会取得非常好的效果,但是本实验训练数据量有限(10万),这造成基于BERT模型的化简效果较差.另外,本文所研究的非多项式混合布尔算术表达式在表示成图后,图表示的复杂性将大幅高于相应的字符序列表示方式,这大幅提升了图序列神经网络学习非多项式混合布尔算术表达式语义的难度,进而造成图序列神经网络模型较难化简非多项式混合布尔算术表达式.
本文的第2个实验测试相关工具化简非多项式混合布尔算术表达式的化简效果,即比较表4中的正确化简结果在化简前后表达式的复杂度,实验结果如表5所示.

表5 化简结果的复杂度Table 5 Complexity of the simplification results
从表5可知,对于所有能正确化简的样本,各种方法化简后的表达式复杂度都有明显的降低,比如其表达式平均长度这一指标被控制在10个字符左右.但是,SSPAM的化简效果表现最差,这是因为该方法依赖模式库中的规则,对于不在模式中的规则其化简效果有限.相比于NeuSim,相关工具(MBA-Blast,MBA-Solver,和Syntia)的化简结果更为简洁.这主要是因为现有工具只能处理一些简单和规则的非多项式混合布尔算术表达式,而NeuSim可以处理更复杂多样的表达式,表6给出了一个具体的化简示例.
从表6可知,已有工具在面对表中的复杂表达式时,通常不能输出化简结果或者输出一个错误的化简结果.而在NeuSim的输出结果中,基于LSTM和GRU的模型输出正确的化简结果,基于BERT的模型输出语义正确但形式上稍显不同的结果,而图序列模型给出了一个错误的化简结果.

表6 化简示例Table 6 Simplification samples
最后,本文横向对比基于不同神经网络模型的NeuSim训练时间,实验结果如表7所示.从表中可知,基于图序列的神经网络模型训练时间最短,为1.0秒每批次,这得益于其模型参数较少,且非循环结构有利于模型的并行化处理,从而加速模型的训练进程.

表7 神经网络模型的训练时间Table 7 Training time of NeuSim
5 总 结
混合布尔算术表达式是指混合使用位运算符和算术运算符的表达式,它已经被多个软件混淆项目所采用.目前已有的反混淆方法都不能有效化简非多项式混合布尔算术表达式,针对该挑战,本文提出一种端到端的解决方案NeuSim.并且分别构建基于序列到序列架构和图序列架构的神经网络模型,并用这些模型来学习和化简非多项式混合布尔算术表达式.同时,本研究收集并构建了一个包含1000000条非多项式混合布尔算术表达式的数据集,并将其用于神经网络模型的训练.相关实验结果表明,NeuSim化简非多项式混合布尔算术表达式的的正确率大幅领先于已有的解决方案,并且其化简时间可以忽略不计.

