近似保序序列模式挖掘
刘 锦,武优西,王月华,李 艳
1(河北工业大学 人工智能学院,天津 300401) 2(河北工业大学 经济管理学院,天津 300401)
1 引 言
序列模式挖掘[1]是数据挖掘[2]的一个热门领域,在近年来获得了信息产业的极大关注.随着网络信息技术[3]的飞速发展,序列模式挖掘在大数据时代的重要性和必要性日益凸显,由于序列模式挖掘具有高效、可解释性强的特性,目前已被广泛应用在生物信息学[4]、疾病检测[5,6]、市场营销[7]、网络安全[8,9]等领域.时间序列数据[10]作为一种常见而重要的数据,广泛存在于人类的生产生活中,与字符序列不同,时间序列数据是按照时间顺序排列而成的数值序列,蕴含着大量的规律信息,为了快速有效地获得其中有价值的信息,研究者们提出了诸多时间序列分析方法,如序列模式挖掘方法[11]、离散短时傅里叶变换法[12]和逻辑回归法[13]等.
然而在一些实际应用中,有时元素值的变化趋势要比元素值本身更有意义.例如在股票分析中,股票的变化趋势要比股票的实际价格更值得研究;在气温预测方面,气温的变化显然比气温数值的大小更有意义,因此保序序列模式挖掘应运而生.保序序列模式挖掘是序列模式挖掘的一个新的分支,它适用于时间序列,关注的是元素值的变化趋势而不是数值大小,所以它能挖掘出现频率较高的趋势图.保序序列模式挖掘保证了时间序列的连续性,挖掘出的代表性趋势使得人们可以更好地认识事物的内在变化规律.为了可以灵活地挖掘保序模式,本文提出基于(δ-γ)距离的近似保序序列模式挖掘算法(Approximate Order Preserving Pattern Mining,AOPM),用来挖掘近似程度不同的保序模式.下面通过例1来说明近似保序序列模式挖掘问题.
例1.时间序列S=(19,16,21,18,20,13,8,22,5,11,18,15,19,12,6,11),minsup=2.
若采用近似保序序列模式挖掘算法,可以挖掘出时间序列S中频繁出现的趋势图(如图1所示).如当δ=0,γ=0时,可以挖掘出两个子序列S1(18,20,13,8)和S2(15,19,12,6),它们的保序模式完全相同,都为(3,4,2,1).当δ=1,γ=2时,则可以挖掘出更长的保序模式,如两个子序列S3(16,21,18,20,13,8)和S4(11,18,15,19,12,6),它们的保序模式分别为(3,6,4,5,2,1)和(2,5,4,6,3,1).S3和S4的保序模式虽然不完全相同,但与保序模式(3,5,4,6,2,1)具有很高的相似性,这是因为S3和S4与它在每个位置的局部误差都满足≤δ=1,总误差满足≤γ=2,可以认为保序模式(3,5,4,6,2,1)的相似趋势在S中出现了两次,满足最小支持度阈值,因此(3,5,4,6,2,1)是一个频繁的近似保序模式.
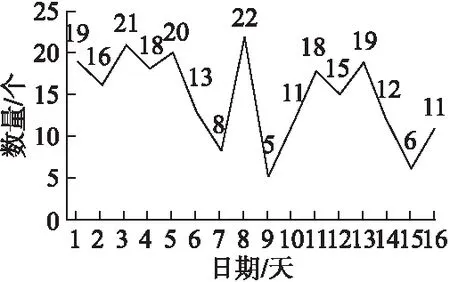
图1 时间序列S的趋势变化图Fig.1 Trend graph of the time series S
本文的贡献如下:
1)为了可以灵活地挖掘保序序列模式,提出了局部误差不超过δ且整体误差不超过γ的近似保序模式挖掘问题.
2)为了完备地解决这个问题,我们提出了AOPM算法.在生成候选模式方面,采用了前后缀拼接的模式融合策略,不会生成无意义的候选模式,减少了候选模式的范围.在模式支持度计算方面,首选获取候选模式的全部候选序列,然后在进行模式匹配.
3)在真实的时间序列数据集上进行了对比实验,验证了AOPM算法的完备性和高效性.
本文剩余部分安排如下:第2节总结相关工作;第3节给出了AOPM问题的相关定义;第4节提出AOPM算法,并分析算法的时空复杂度;第5节验证AOPM算法的性能;第6节得出了本文结论.
2 相关工作
序列模式挖掘作为当前的研究热点之一旨在快速找出满足用户特定需求的模式,针对不同问题,已经衍生出多种形式的挖掘方法,如间隙约束挖掘方法[14,15]、负序列挖掘方法[16]、高效用挖掘方法[17]、序列规则挖掘方法[18]等.序列模式挖掘方法可以采用多种形式进行划分,如模式支持度计算方式的不同和挖掘数据性质的不同等角度进行划分.
根据模式支持度计算方式的不同,可以将序列模式挖掘分为精确序列模式挖掘和近似序列模式挖掘.Lin等人采用PAA方法将时间序列进行分段并对求每段的平均值,然后再挖掘其中的频繁模式;Min等人根据数据波动将数字时间序列转换为字符型序列,并运用在具有弱通配符间隙的模式挖掘中,这些研究都属于精确序列模式挖掘.而Bae等人利用效用容忍因子计算模式的可信效用,进而从噪声数据库中提取鲁棒的高效用模式则属于近似序列模式挖掘.
根据挖掘数据性质的不同,又可以将序列模式挖掘分为字符序列模式挖掘[19]和时间序列挖掘[20].字符序列模式挖掘主要针对DNA序列和基因序列等由字符构成的字符型序列,挖掘字符序列通常是为了解决生物信息学中的问题.时间序列挖掘的对象则是由连续变化的数值构成的数值型序列,通常首先采用SAX算法将时间序列符号化[21,22],然后在使用不同的方法进行挖掘,如计算时间序列的先验移动平均的方法、线性回归的方法等.保序模式挖掘的对象就是时间序列,通过挖掘其中频繁出现的趋势图,可以帮助人们进行分析和预测,如股票市场的股价波动分析,某个地点的气温变化分析以及用户行为分析[23]等.
由于时间序列具有高维性、连续性等特点,直接对其进行挖掘是非常困难的,需要通过一系列转换将原始的数值型数据转换为其它域的数据再进行挖掘,转换的实质就是对时间序列模式来进行重新表示.保序模式匹配问题就与时间序列的次序关系表示紧密相关,基于次序关系的表示与数值型表示并不相同,数值型表示是原始的时间序列数据,而次序关系则是用元素在序列中的秩次进行表示的,所以有相对顺序的概念.Kim等人[22]首先将元素之间的次序关系定义为二元关系(<,>),并提出了相对顺序的前缀表示和最近邻表示,但没有考虑元素间数值相等的情况.然而两个数值之间的次序关系实际上是三元(<,=,>)的,因此Cho等人[23]对其进行了扩展,将二元关系扩展为三元关系,并设计了一种即使存在元素相等的情况,也能判断两个字符串是否顺序同构的算法.它要求模式与子序列的相对顺序完全相同,能快速定位与已知模式趋势变化完全相同的子序列,为此,Wu等人[24]提出了保序模式挖掘算法OPP-Miner,用来发现时间序列中的隐藏规律.上述研究属于精确匹配的研究.而在一定数据噪音存在的场景下,需要研究近似模式匹配,如Wu等人允许模式和匹配子序列之间存在数据噪声,提出了一种带长度约束的(δ-γ)近似预测方法,用来找到更加有价值的模式.又如Paw等人[25]提出基于Hamming距离度量相似度的匹配的精确度,若两个字符串在相同位置删除最多k个元素后具有相同的相对顺序则匹配成功,但该问题的匹配结果存在偏差,因为无法度量子序列与模式之间的局部近似度.Juan等人[26]提出基于(δ-γ)距离的相似度度量方法改善了此问题,采用局部-整体约束,提高了匹配的精确度.表1给出了相关研究工作对比.

表1 相关研究工作对比Table 1 Comparison of related research work
从表1可以看出:文献[24]与本文的研究最为相近,不同之处在于文献[24]是精确的保序模式挖掘,而本文是保序模式的近似挖掘.文献[26]是基于(δ-γ)距离的保序模式匹配,而本文研究的是保序模式挖掘.文献[25]是基于Hamming距离的保序模式匹配,而本文是(δ-γ)距离近似.本文将(δ-γ)保序匹配引入到保序模式挖掘中来,挖掘不同约束条件下的频繁趋势图,适应了更多的应用领域,更好地帮助人们进行分析和预测.
3 相关定义
定义1.时间序列:由n个有序的连续数值构成的时间序列可以表示为S=s1s2…si…sn(1≤i≤n),其中si可以称为元素.
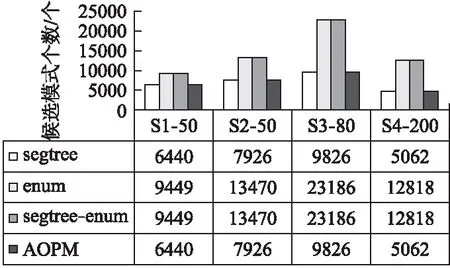
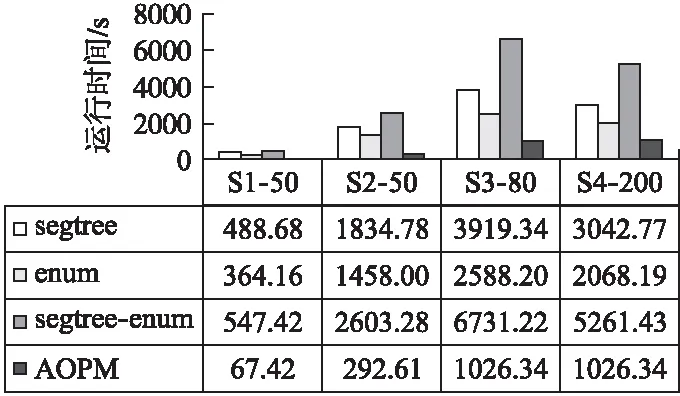
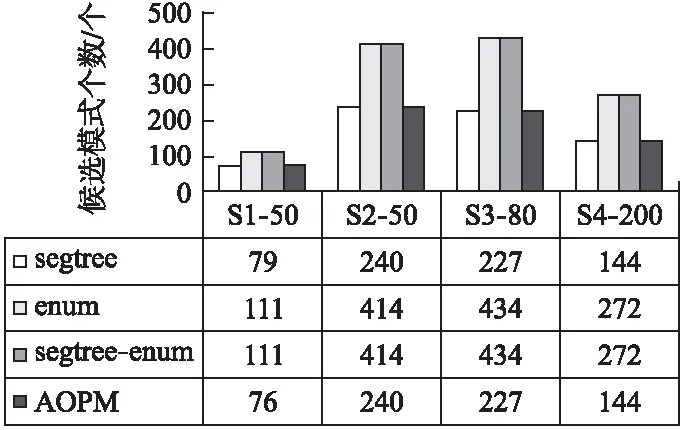
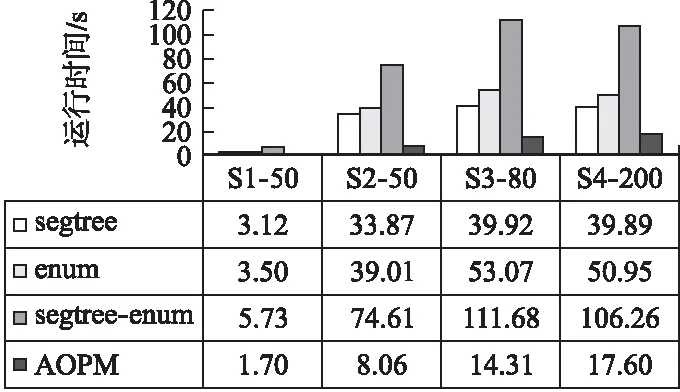
定义2.秩次:元素pi在长度为m的模式P=p1p2…pi…pm(1≤i≤m)中的秩次记作rankp(pi)=1+|{x|px 定义3.相对顺序和保序模式:长度为m的模式P的相对顺序为rankp(p1)rankp(p2)rankpp(p3)…rankp(pm),由相对顺序所表示的模式就是保序模式. 例2.给定模式P=(19,16,21,18),由于元素19在模式P中第3小,因此其秩次rankp(19)=3;类似的,元素16在模式P中最小,因此rankp(16)=1.进而其保序模式r(P)=(3,1,4,2). 定义5.(δ-γ)保序出现:对于一个长度为m的保序模式P,若在时间序列S中能找到一个长度也为m的子序列T,使得P与T的保序模式r(T)满足(δ-γ)距离约束,则称T是保序模式P在时间序列S中的一次(δ-γ)保序出现,其中δ和γ是两个给定的非负整数. 定义6.频繁保序模式:如果保序模式P在时间序列S中的(δ-γ)保序出现数不小于用户给定的最小支持度阈值(minsup),则称P为一个频繁的(δ-γ)保序模式. 例3.给定δ=1,γ=2,P=(3,2,4,1),S=(19,16,21,18,20,13,8,22,5,11,18,15,19,12,6,11).在时间序列S中可以找到子序列S1=(19,16,21,18),将S1转化为保序模式后得r(S1)=(3,1,4,2),P与r(S1)进行(δ-γ)保序匹配:|3-3|=0≤δ,|2-1|=1≤δ,|4-4|=0≤δ,|1-2|=1≤δ;0+1+0+1=2≤γ,因此,P和S1满足(δ-γ)距离约束,S1为P在时间序列S中的一次(δ-γ)保序出现.同理,P在时间序列S中的另外3个(δ-γ)保序出现分别为S2=(21,18,20,13),S3=(13,8,22,5),S4=(18,15,19,12). 定义7.近似保序模式挖掘:用户通过自定义参数值,在给定的时间序列S中找到所有满足最小支持度阈值的频繁保序模式. 例4.时间序列S=(19,16,21,18,20,13,8,22,5,11,18,15,19,12,6,11),δ=1,γ=2,minsup=4,挖掘出所有的频繁(δ-γ)保序模式. 在时间序列S中挖掘得到的频繁近似保序模式集F={(1,2),(2,1),(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1)(3,2,4,1),(3,4,1,2),(4,3,2,1)}. 当δ=γ=0时,近似保序序列模式挖掘转化为精确保序序列模式挖掘,因此本文研究是更具一般性研究. 对于近似保序模式挖掘,关键的两个步骤是候选模式的生成和(δ-γ)保序模式支持度的计算.4.1节介绍了候选模式生成策略;4.2节介绍了候选模式支持度计算策略;4.3节介绍了AOPM算法;4.4节对AOPM算法及其对比算法进行了时空复杂度分析. 4.1.1 枚举策略 枚举策略是一一列出所有可能出现的情况的策略,假设一个长度为m(1 例5.长度为3的频繁模式集合Fre3={(1,3,2),(2,1,3)},采用枚举策略生成长度为4的候选模式集C4,结果如下表2所示. 表2 基于枚举策略生成候选模式集C4Table 2 Generate candidate pattern set C4 based on enumeration strategy 以模式(1,3,2)为例,生成长度为4的候选模式有以下4种情形:1)新增加的元素小于原始的3个元素时则生成候选模式(2,4,3,1);2)新增加的元素的数值只比第一个大则生成候选模式(1,4,3,2);3)新增加的元素比最小的两个元素数值都大则生成候选模式(1,4,2,3);4)新增加的元素大于原始的3个元素时则生成候选模式(1,3,2,4).由于每个模式可以生成4个候选模式,那么2个频繁模式就可以产生出2×4=8个候选模式. 显然候选模式数量越多,挖掘速度越慢.下一小节中,本文将提出更加高效的模式融合策略减少候选模式的生成. 4.1.2 模式融合策略 定义8.前缀子模式和保序前缀子模式、后缀子模式和保序后缀子模式:给定序列模式P=(p1p2…pm),除去最后一个元素pm后剩余的子模式Q=(p1p2…pm-1)就是模式P的前缀子模式,保序前缀子模式就是前缀子模式的保序模式,记做prefixorder(P);除去第一个元素p1后剩余的子模式H=(p2p3…pm)就是模式P的后缀子模式,保序后缀子模式就是后缀子模式的模式,记做suffixorder(P). 定义9.模式融合:假设有两个长度都为m的模式P=(p1p2…pm)和Q=(q1q2…qm),当模式P的后缀子模式的保序模式与模式Q的前缀子模式的保序模式一致时,即suffixorder(P)=prefixorder(Q),则P和Q就可以拼接生成长度为m+1的超模式;这里存在3种情况: 情况1.p1>qm.此时产生一个超模式T,其中t1=p1+1,然后将qj(1≤j≤m)与p1进行比较,若qj>p1,那么tj+1=qj+1,否则,tj+1=qj. 情况2.p1=qm.此时产生两个超模式T和K,在拼接为模式T=(t1t2…tmtm+1)时,首先令t1=p1+1,然后将qj(1≤j≤m)与p1进行比较,若qj>p1,那么ti+1=qj+1,否则,ti+1=qj;在拼接为模式k=(k1k2…kmkm+1)时,km+1=qm+1,然后将pi(1≤i≤m)与qm进行比较,若pi>qm,那么ki=pi+1,否则,ki=pi. 情况3.p1 例6.给定保序模式P=(2,3,1),其分别与模式Q=(3,2,1)和模式R=(3,1,2)进行拼接. 首先求出模式P的后缀、模式Q和R的前缀模式分别为:suffix(P)=(3,1)和prefix(Q)=(3,2),prefix(R)=(3,1).他们的保序模式分别为:suffixorder(P)=(2,1),prefixorder(Q)=(2,1),prefixorder(R)=(2,1).因为suffixorder(P)=prefixorder(Q)=(2,1),且1<2,满足情况1,故P和Q可拼接为一个长度为4的模式T,因为p1>q3,所以令t1=p1+1=3,然后将q1、q2和q3别与q3进行比较,因为q2和q3都不大于p1,q1大于p1,所以(t2t3t4)=(4,2,1),综上T=(3,4,2,1). 又因为suffixorder(P)=prefixorder(R)且2=2,满足情况2,故P和R拼接可生成两个长度为4的模式T和K.在生成T时,令x1=p1+1,因为r3≤p1,所以令x4=r4,因为r1>p1,所以x2=r2+1,因为r2、r3≤p1,所以x3=r2、x4=r3、最终得到X=(3,4,1,2);在生成K时,令k4=r4+1,因为q1、q3≤r3,所以k1=q1、k3=q3,因为q2>r4所以k2=q2+1,最终可得到K=(2,4,1,3). 例7.本文使用与例5相同的频繁模式集Fre3,通过模式融合策略来生成4长度候选模C4. 3长度的频繁模式F3的第一个模式是(1,3,2),(1,3,2)的后缀模式为(3,2),它的相对顺序是(2,1),然后开始从上到下顺序遍历F3中的模式,当找到一个前缀的相对顺序也为(1,2)的模式时,就将这两个模式进行模式拼接,经过一次循环之后,能够在模式(1,3,2)的基础上生成(1,3,2,4)这个4长度的候选模式,再次对F3的第二个模式(2,1,3)进行同样的操作,不停地循环上述步骤,直到长度为3的频繁模式集合中的最后一个模式被处理完,这样就找到了全部的长度为4的候选模式,拼接结果如表3所示. 表3 基于模式融合策略生成候选模式集C4Table 3 Candidate pattern set C4 generated based on pattern fusion strategy 通过对比表2和表3可以看到,如果采用枚举策略会生成8个长度为4的候选模式,而当采用基于前后缀拼接的模式融合策略生成候选模式时,只生成了3个长度为4的候选模式.因此,模式融合策略可以有效地减少候选模式的数量,从而提高算法的挖掘效率. 算法1.Generate算法: 输入:长度为m的频繁模式Fm 输出:下一长度的候选模式数组C 1.fori=1 toFm.size do 2. forj=1 toFm.size do 3. q←suffixorder(Fm[i]) 4. r←prefixorder(Fm[j]) 5. if q=r then 6. if(Fm[i][1]=Fm[j][m])then 7. c1∪c2←Fm[i]⨁Fm[j] 8.C←c1 9.C←c2 10. else 11. c←Fm[i]⨁Fm 12.C←c 13. end if 14. end for 15.end for 16.returnC 4.2.1 候选序列查找 对每一个候选模式,在进行(δ-γ)保序匹配之前首先要从头到尾扫描时间序列S来找到它的所有候选序列,下面通过例8来具体介绍. 例8.给定S=(19,16,21,18,20,13,8,22,5,11,18,15,19,12,6,11),在minsup=4,δ=1,γ=2的情况下找到候选模式(4,3,5,1,2)的候选序列. 对每一个候选模式,我们通过从头到尾扫描数据库的方法来找到所有的候选序列,找的第1个候选序列是(19,16,21,18,20),第2个候选序列是(16,21,18,20,13),以此类推,直至到S的结尾.候选模式(4,3,5,1,2)的全部候选序列结果集C={(19,16,21,18,20),(16,21,18,20,13),(21,18,20,13,8),(18,20,13,8,22),(20,13,8,22,5),(13,8,22,5,11),(8,22,5,11,18),(22,5,11,18,15),(5,11,18,15,19),(11,18,15,19,12),(18,15,19,12,6),(15,19,12,6,11)}. 4.2.2 支持度的计算 为快速计算支持度,对每个候选模式,将它的候选序列通过排序算法都转化为保序模式,然后将该候选模式与它的所有候选序列进行(δ-γ)保序匹配,如果匹配成功,则该模式的支持度加一.将所有的候选序列匹配完成后,如果该候选模式的支持度大于等于给定的支持度阈值,则该模式就是一个频繁的(δ-γ)保序模式,将其存储到最终的频繁模式数组中.如此循环,直到找到该长度的所有频繁(δ-γ)保序模式. 算法2.Match算法: 输入:候选模式数组C 输出:满足最小支持度阈值的(δ-γ)保序模式 1.fori=1 toC.size do 2. c←C[i] 3. forj=1 toS.size do 4. Scan the time seriesSto generate the candidate sequences of c 5. The candidate c is matched with its candidate sequences to get the supportnumber 6. ifnumber≥minsupthen 7.Fm←c 8. end if 9. end for 10.end for 11.returnFm 例9.时间序列S=(19,16,21,18,20,13,8,22,5,11,18,15,19,12,6,11),δ=1,γ=2,minsup=4,挖掘出所有的近似保序模式. 长度为1的模式是一个点,不代表趋势变化,因此从2长度的模式开始挖掘.2长度的保序模式只有上升(1,2)和下降(2,1)两种趋势,即C2={(1,2),(2,1)},分别计算它们的支持度,它们的支持度都不小于给定的最小支持度,所以2长度的频繁模式F2={(1,2),(2,1)};然后用这两个2长度的频繁模式生成3长度的候选模C3={(1,2,3),(2,3,1),(1,3,2),(3,1,2),(2,1,3),(3,2,1)},分别计算它们的支持度,得到3长度的频繁模式F3={(1,2,3),(2,3,1),(1,3,2),(3,1,2),(2,1,3),(3,2,1)},迭代上述过程得到4长度的频繁模式F4={(3,2,4,1),(3,4,1,2),(4,3,2,1)},F5={}.最终挖掘得到的近似保序模式F={(1,2),(2,1),(1,2,3),(2,3,1),(1,3,2),(3,1,2),(2,1,3),(3,2,1),(3,2,4,1),(3,4,1,2),(4,3,2,1)}. 算法3.AOPM算法: 输入:序列数据集S,局部约束δ,全局约束γ,最小支持度阈值minsup 输出:频繁(δ-γ)保序模式集合F 1.Scan time sequenceS,calculate the support of each pattern in the candidate pattern set {(1,2),(2,1)} of length 2,and put the frequent pattern intoF2 2.m←2 3.C←Generate(F2) 4.whileC!=null do 5.Fm←Match(C) 6.m←m+1;C←Generate(Fm) 7.end while 8.returnF AOPM算法与其对比算法(将会在下节中介绍)的时空复杂度对比如表4所示,其中,m,n,N分别表示模式长度、序列长度和候选模式个数. 表4 相关算法时空复杂度比较Table 4 Comparison of time and space complexity of related algorithms 5.1节对本文的实验环境和实验数据进行了说明;5.2节介绍了本文所使用的对比算法;5.3节验证了AOPM算法的完备性和高效性. 实验运行的环境为:Intel(R)Core(TM)i7-6560U处理器,主频2.20GHz,内存容量16GB,Windows 10,64位操作系统的计算机,程序开发环境为VS2017.对比实验数据集分别为黄金、石油、罗素2000指数和纳斯达克指数的收盘价格.数据集的具体描述如表5所示. 表5 实验数据集Table 5 Experimental data sets 1)segtreeBA:为了验证AOPM算法中(δ-γ)保序匹配算法的高效性,将AOPM算法中(δ-γ)保序匹配算法替换为segtreeBA算法来进行对比.segtreeBA算法是文献” New algorithms for δγ-order preserving matching ”中使用的(δ-γ)保序匹配算法,该算法建立了一个树形结构即segment tree,并给segment tree建立了3个标准操作函数分别为:buildSegTree()函数、updateSegTree()函数和querySegTree()函数. 2)enum:为了验证AOPM算法中候选模式生成策略的高效性,将其与enum算法进行对比,enum算法使用了枚举的候选模式生成策略. 3)segtreeBA-enum:segtreeBA-enum采用了segtreeBA算法的模式匹配策略和枚举的候选模式生成策略来与AOPM算法进行整体运行效率上的对比. 5.3.1 近似挖掘 本文在δ=2,γ=4的条件下来进行近似挖掘,minsup则根据数据集的长度不同而采取不同的值.实验结果如图2和图3所示. 图2 SDB1-SDB4数据集中产生的候选模式数量对比Fig.2 Comparison of the number of candidate patterns generated in the SDB1-SDB4 data sets 图3 SDB1-SDB4数据集中4种算法运行时间对比Fig.3 Comparison of the running time of the four algorithms in the SDB1-SDB4 data sets 通过实验,可以得出以下结论: 1)因为这4种算法在每个数据集上都使用了相同的挖掘条件,所以这4种算法在SDB1-SDB4数据集上都挖掘出了相同数量的频繁保序模式. 2)由图2的挖掘结果可知:AOPM算法、segtreeBA算法生成了相同数量的候选模式,因为它们都采取了模式融合的候选模式生成策略;enum算法、segtreeBA-enum算法也生成了相同数量的候选模式,它们都采取了枚举的候选模式生成策略.因为模式融合策略不会生成无意义的候选模式,即会筛选掉一些不可能是频繁模式的候选模式,所以使用模式融合策略的算法要比使用枚举策略的算法生成的候选模式少. 3)AOPM算法与segtreeBA算法相比,采取了相同的候选模式生成策略但采取了不同的模式匹配策略.与AOPM算法相比,segtreeBA算法每进行一次(δ-γ)保序匹配都要使用querySegTree()和updateSegTree()函数来对segment tree进行更改恢复操作,这就增加了(δ-γ)保序匹配时的时间复杂度,而AOPM算法则无需更改原时间序列.由图3可知,在SDB1~SDB4数据集上segtreeBA算法的运行时间要比AOPM算法的运行时间长. 4)AOPM算法与enum算法相比,采取了相同的模式匹配策略而采取了不同的候选模式生成策略.enum算法使用了枚举的候选模式生成策略,生成候选模式的时间复杂度为O(mN),随着挖掘的进行候选模式m的长度会越来越大,所以与AOPM算法相比,enum算法会生成更多的候选模式进而增加了时间复杂度.由图3可知,enum算法的运行时间要比AOPM算法的运行时间长. 5)segtree-enum算法无论是模式匹配还是候选模式生成都采取了与AOPM算法不同的策略,所以segtree-enum算法的运行时间相当长,在图3的4个数据集上segtreeBA-enum算法所需的运行时间都是AOPM算法的几倍乃至十几倍,由此可知AOPM算法所使用的模式匹配策略和候选模式生成策略配合使用是非常高效的.综上所述可以得出:AOPM算法是一个完备性和高效性的算法. 5.3.2 精确挖掘 本文在在δ=0,γ=0的条件下来进行精确挖掘,minsup根据数据集的长度不同而采取不同的值.实验结果如图4和图5所示. 图4 SDB1-SDB4数据集中产生的候选模式数量对比Fig.4 Comparison of the number of candidate patterns generated in the SDB1-SDB4 data sets 图5 SDB1-SDB4数据集中4种算法运行时间对比Fig.5 Comparison of the running time of the four algorithms in the SDB1-SDB4 data sets 在相同的挖掘条件下,4种挖掘算法挖掘出了相同数量的频繁保序模式.由图4可知,当挖掘的频繁模式个数相同时,AOPM算法和segtreeBA算法生成了相同数量的候选模式,因为它们都采取了模式融合的候选模式生成策略;enum算法和segtreeBA-enum算法也生成了相同数量的候选模式,它们都采取了枚举的候选模式生成策略.在运行速度方面,由图5可知,与近似保序挖掘一样,因为AOPM算法所用策略使得挖掘过程更加简便,所以要比其它对比算法运行速度快,从而验证了AOPM算法在精确挖掘条件下也是一个挖掘效率较高的保序模式挖掘算法. 为了在时间序列中挖掘有价值的信息,本文提出了近似保序序列模式挖掘,并提出了近似保序序列模式挖掘算法:AOPM算法.该算法能够在时间序列中挖掘近似程度不同的保序模式,更好地帮助人们进行分析和预测.在候选模式生成方面,AOPM算法使用了模式融合策略.该策略在不遗漏任何有效解的情况下,显著减少了候选模式的数量.在计算模式支持度时,AOPM算法首选获取候选模式的全部候选序列,然后在进行模式匹配.但AOPM算法仍需重复扫描数据库来计算模式支持度,后期的研究可以着重于如何避免重复扫描数据库来提高挖掘效率.本文通过在真实时间序列数据集上的进行实验,实验结果表明AOPM算法是一个完备性和高效性的保序模式挖掘算法.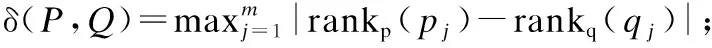
4 AOPM
4.1 候选模式生成


4.2 支持度计算
4.3 AOPM算法
4.4 算法时间和空间复杂度
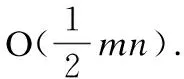

5 实验结果与性能分析
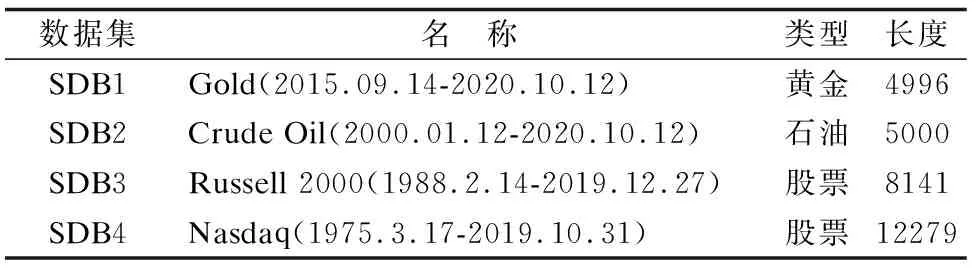
5.1 数据集
5.2 对比算法
5.3 挖掘实例
6 结 论

