基于宽度混合森林回归的城市固废焚烧过程二噁英排放软测量

夏 恒 汤 健 崔璨麟 乔俊飞

本文缩写词的详细解释见表1.

表1 符号说明Table 1 Symbol description

城市固废焚烧是目前世界范围内解决 “垃圾围城”困境的主要方式之一,具有无害化、减量化和资源化等显著优势[1-2].目前中国MSWI 的处理能力占比已超过50%,污染排放监管力度也逐渐加强[3].二噁英作为MSWI 过程排放的有组织废气中具有持久性和剧毒性的有机污染物[4],是造成焚烧建厂存在 “邻避现象”的主要原因[5],也是MSWI 过程必须最小化控制的重要环保指标之一[6-7].基于高分辨气相色谱/高分辨质谱的离线化验分析方法是目前DXN 排放浓度检测的主要手段[8],存在技术难度大、时间滞后性大、人力与经济成本高等缺点,已成为阻碍MSWI 过程实现实时优化控制的关键因素之一.因此,DXN 排放浓度的在线检测是MSWI 过程的首要挑战问题[3].

针对上述问题,利用可在线检测的DXN 关联物构建映射模型进而获得DXN 浓度的在线间接检测方法成为热点[9-10];然而,其存在设备复杂、成本高、干扰因素多、预测精度无法保证等问题[11],同时其在本质上也是一种结合数据建模的检测手段.相较于离线分析和在线间接检测方法而言,基于工业集散控制系统采集的易检测过程数据驱动的软测量技术是解决DXN 无法在线检测问题的有效途径,具有稳定、精准和快速响应等特点[3].软测量技术已在石油、化工和炼钢等复杂工业过程的难测参数检测中广泛应用[12-15].

目前,面向DXN 排放浓度的软测量研究可分为基于单学习器和基于集成多学习器两个方向.针对前者: Chang 等[16]采用遗传规划结合神经网络对欧美等多个国家焚烧厂的Polychlorinated dibenzop-dioxins/Polychlorinated dibenzofurans 排放进行建模,其数据涉及多种不同类型的焚烧炉,导致模型不具有良好的应用性;Bunsan 等[17]通过多次重复实验确定反向传播神经网络结构后构建软测量模型,但其不具有良好的移植性且BPNN 面对小样本时存在过拟合、稳定性差等问题;针对上述基于NN的软测量方法存的问题,肖晓东等[18]利用支持向量回归[19]构建基于国内MSWI 过程实际数据的软测量模型,但存在核函数、惩罚系数等超参数难以确定的问题;进一步,乔俊飞等[20]针对北京某MSWI 电厂的高维过程数据,设计了基于多层特征选择策略的软测量模型,但约简特征模型的泛化性能有待提高.

从机理视角,DXN 排放浓度与MSWI 过程的多个工艺阶段的众多过程变量均具有相关性,并且在不同工况下也存在差异性;此外,获取DXN 浓度检测真值存在难度大、成本高的缺点,使得建模数据的小样本、高维度特性成为DXN 软测量面临的主要问题.上述因素导致基于单学习器的软测量模型难以获得较佳检测精度.因此,基于集成多学习器的软测量模型成为当前的研究热点,其包括: 汤健等[21]基于选择性集成思想设计了一种自适应确定SVR 超参数的软测量方法,采用文献[22]的数据进行验证,但测量精度有待提高;在此基础上,汤健等[23]采用变量投影重要性评价和设定特征约简比率的策略对北京某MSWI 过程的DXN 建模数据进行维数约简后,构建能够自适应确定核参数的SEN 软测量模型,进一步提高了检测精度;针对上述方法存在的放弃部分特征可能导致的信息丢失问题,Xia 等[24]通过随机森林和梯度提升树的混合集成策略进行DXN 软测量模型构建,但模型结构过于复杂且运行时间较长,不适用于实际应用;进一步,借鉴NN 模式和非NN 模式深度学习在提取深层次表征特征方面的突出性能[25-26],Tang 等[27-28]提出了面向小样本高维数据的深度森林回归算法并用于构建DXN 软测量模型,但检测精度仍有待进一步提高;在此基础上,Xu 等[29]采用主成分分析对高维过程数据进行特征提取后再基于DFR 构建软测量模型,虽然提升了模型的泛化性能但约简后的潜在特征已不具备物理意义.显然,上述集成学习策略均存在训练难度大、模型复杂度高以及收敛速度慢等问题.

近年来,宽度学习通过先扩展模型网络 “宽度”再采用Moore-Penrose 逆矩阵[30]获取权重的方式构建模型,具有收敛速度快、超参数少和精度高等优势[31-32].现有的BLS 研究主要基于NN 模式,已在图像识别[33-35]、故障诊断[36-38]和工业过程控制[39-41]等多个领域广泛应用.但是,上述研究均是在低特征维数、大样本数据集的研究背景下进行的应用与探索[39,42].面向高特征维数、小样本数据集[43]的BLS研究还未见报道.

针对上述问题,以MSWI 过程DXN 排放浓度检测为目标,提出了基于宽度混合森林回归的建模算法.主要创新工作为:

1)基于BLS 框架的优势,提出了具有特征映射层、潜在特征提取层、特征增强层和增量学习层结构的BHFR 建模算法.

2)利用RF 和完全随机森林组成的混合森林组替代BLS-NN 神经元组,实现对高维特征向量的映射.

3)基于PCA 的潜在特征提取和互信息度量准则,以保证全联接混合矩阵中潜在有价值信息的最大化传递和最小化冗余.

4)通过增量式学习策略构建以混合森林组作为最小单位的增量学习层,采用Moore-Penrose 伪逆获得权重矩阵.

在高维基准数据集和MSWI 过程DXN 数据集上的实验结果表明了本文方法的有效性和优越性.

1 面向DXN 排放的MSWI 过程描述

MSWI 过程包含固废储运、固废燃烧、余热交换、蒸汽发电、烟气净化和烟气排放等工艺阶段,以日处理量800 吨的北京某炉排式MSWI 过程为例,其工艺如图1 所示.

图1 城市固废焚烧工艺流程图Fig.1 Process flow chart of municipal solid waste incineration process

结合DXN 分解、生成、吸附和排放的全流程对各阶段的主要功能描述如下:

1)固废储运阶段.环卫车辆从城市各收集站点将城市固废运输至MSWI 电厂,经称重记录后从卸料平台倾倒至固废储存池中未发酵区,然后由固废抓斗对其进行混合搅拌,再抓取至发酵区,经3～ 7天发酵和脱水以保证MSW 焚烧的低位热值[44].研究表明,原生MSW 中存在微量DXN (约0.8 ng TEQ/kg),并含有DXN 生成反应所需的多种含氯化合物[5].

2)固废燃烧阶段.固废抓斗将发酵后的MSW投放至进料斗,经进料器将MSW 推送到焚烧炉内,依次经过干燥、燃烧1、燃烧2 和燃烬炉排后,MSW 中的可燃成分随之完全燃烧;所需助燃空气由一次风机和二次风机从炉排下方和炉膛中部注入,最终燃烧产生的灰渣从燃烬炉排末端落至捞渣机,经水冷后送入炉渣池.研究表明,启炉和停炉期间因工况波动频繁导致所产生的DXN 量级远远高于正常运行期间[45].为保证原生MSW 中含有的以及焚烧时产生的DXN 在炉内能够被完全分解,炉膛燃烧过程需满足: 严格控制烟气温度在850 ℃以上、高温烟气在炉内停留时间超过2 秒、确保足够大的烟气湍流度等工艺要求[46].

3)余热交换阶段.炉膛产生的高温烟气(高于850 ℃)经引风机抽吸进入余热锅炉系统,先后经过过热器、蒸发器和省煤器设备,与锅炉汽包液态水进行热交换后产生高温蒸汽,进而实现降温处理,使余热锅炉出口的烟气温度低于200 ℃ (即烟气G 1).从DXN 生成机理的角度,高温烟气经余热锅炉降温时,导致DXN 生成的化学过程包括高温气相合成(800 ℃～ 500 ℃)[47]、前驱物合成(450 ℃～ 200 ℃)[48]和从头合成(350 ℃～ 250 ℃)[49]等反应,但目前还暂无统一的定论[50].

4)蒸汽发电阶段.利用余热锅炉产生的高温蒸汽推动汽轮发电机,机械能转变为电能,实现厂级用电的自给自足和剩余电量的上网供应,实现资源化和获取经济效益.

5)烟气净化阶段.MSWI 过程的烟气净化主要包含脱硝、脱硫、脱重金属、吸附DXN 和除尘(颗粒物)等一系列过程,进而实现焚烧烟气污染物排放达标的目的.采用活性炭喷射系统吸附烟气中的DXN 是目前应用最为广泛的技术手段[51],其吸附后的DXN 富集于飞灰中.

6)烟气排放阶段.经降温和净化处理后的含有微量DXN 的焚烧烟气(即烟气G 2)由引风机抽吸后经烟囱排放至大气中.MSWI 过程的不间断、长时间的运行特性导致烟囱内壁颗粒物中附着大量DXN (即记忆效应[52]),但在何种工况下存在释放的可能性还是目前业界未解决的研究难题.

目前,面向MSWI 过程的DXN 软测量检测研究主要集中针对排放阶段(即烟气G 3)的DXN 浓度检测,其对应的过程变量信息如表A1 所示.本文研究重点是构建G 3 烟气处的软测量模型.

表A1 DXN 数据集的过程变量信息Table A1 The process variable information for DXN datasets

表A1 DXN 数据集的过程变量信息 (续表)Table A1 The process variable information for DXN datasets (continued table)

表A1 DXN 数据集的过程变量信息 (续表)Table A1 The process variable information for DXN datasets (continued table)

表A1 DXN 数据集的过程变量信息 (续表)Table A1 The process variable information for DXN datasets (continued table)

2 基于宽度混合森林回归的建模策略

本文BHFR 建模策略包含特征映射层、潜在特征提取层、特征增强层和增量学习层4 个主要部分,如图2 所示.

图2 宽度混合森林回归建模策略图Fig.2 Modeling strategy of broad hybrid forest regression

各部分的主要功能如下:

2)潜在特征提取层.利用PCA 对由X与特征映射层输出ZN组成的全联接混合矩阵[X|ZN] 进行潜在特征提取,去除特征空间的冗余信息,进一步通过所提取的潜在特征与真值y的互信息确定潜在特征维数并得到新的输入数据

3)特征增强层.以X′作为输入,通过特征增强层的K个混合森林组进行特征映射,得到增强层输出矩阵HK;

4)增量学习层.以X′作为输入,以混合森林组为最小单位逐步增加并更新权重WK+P,直到训练误差收敛.

2.1 特征映射层

从本质上讲,BHFR 是以RF 和CRF 为基元构成的混合森林组作为基础映射单元取代原始BLS中的神经元.

以特征映射层的第n个混合森林组为例描述特征映射层的建模过程.对{X,y}进行Bootstrap和RSM 采样,获得混合森林组模型的J个训练子集,表示如下:

式中,L表示决策树叶节点数量,I(·) 表示指示函数,当预测样本属于当前叶节点的样本集时Rl),即将cl作为该样本的?预测值.cl采用递归分裂方式计算,其物理意义是: 第l个叶节点的预测值,由第l个叶节点中所有样本的加权均值所得.

进一步,RF 和CRF 的建模过程如图3 所示.

图3 RF 和CRF 的建模过程Fig.3 Modeling process of RF and CRF

RF 的基本思想为通过Bootstrap 和RSM 构建多个以平方误差为损失函数分裂生长的决策树模型后并行集成,建模步骤如RF 建模过程所示.RF中决策树的分裂损失函数 Ωi(·) 可表示为:

CRF 的基本思想为通过Bootstrap 和RSM 构建多个完全随机分裂生长的决策树模型后并行集成,建模步骤见CRF 建模过程所示.CRF 中决策树的分裂采用完全随机选择方式,可表示为:

被随机分裂的左右树节点输出值为样本真值的期望,如下:

通过上述过程,第n个混合森林组可表示为:

进而,第n个映射特征可表示为:

最终,特征映射层的输出ZN表示为:

式中,ZN包含NRaw个样本和 2N维特征.

算法1.RF 建模步骤

2.2 潜在特征提取层

为了避免信息传递过程中的信息丢失导致的过拟合现象,本文BHFR 采用全联接策略实现特征映射层与特征增强层、增量学习层之间的信息传递.同时,为了保证模型训练过程中信息冗余的最小化,此处采用PCA 提取全联接混合矩阵的潜在特征,再利用互信息进一步筛选与真值信息最大化相关的潜在特征,进而实现对高维数据的降维处理.

首先,原始输入数据X与特征映射矩阵ZN组合得到全联接混合矩阵A,可表示为:

式中,A含NRaw个样本和 (M+2N) 维特征.

接着,考虑到A的维数远高于原始数据,此处利用PCA 最小化A中的冗余信息,计算A的相关矩阵R,如下:

进一步,对R进行奇异值分解,得到(M+2N)个特征值和相应特征向量,如下:

式中,U(M+2N)表示 (M+2N) 阶正交矩阵,Σ(M+2N)表示 (M+2N) 阶对角矩阵,V(M+2N)表示(M+2N)阶正交矩阵.

式中,σ1＞σ2＞···＞σ(M+2N)表示由大到小排列的特征值.

然后,根据设定潜在特征贡献阈值η,确定最终的潜在特征数量QPCA,如下:

式中,QPCA≪(M+2N).

基于上述确定的QPCA个潜在特征,获得特征值集合对应的特征向量矩阵VQPCA,即A的投影矩阵.然后,对A进行特征投影以实现冗余信息的最小化处理,将获得潜在特征记为XPCA,即:

接着,通过信息最大化选择机制以保证所选择潜在特征与真值间的相关性,如下:

2.3 特征增强层

首先对新数据集{X′,y}进行采样,获取混合森林算法的训练子集,如下:

接着,以第k个混合森林组中第j个RF 的构建为例,如下:

进而,可得到特征增强层中第k个混合森林组中的RF 模型为:

然后,类似地以第k个混合森林组中的第j个CRF 的构建为例,如下:

进而,可得到特征增强层中第k个混合森林组的CRF 模型,其表示为:

通过上述过程,得到第k个混合森林组第k个增强特征表示如下:

最后,特征增强层的输出HK表示如下:

当不考虑增量学习策略时,BHFR 模型的表示如下:

式中,GK表示特征映射层与特征增强层输出的组合,即其包含NRaw个样本和(2N+2K) 维特征;WK表示特征映射层和特征增强层与输出层间的权重,其计算如下:

式中,I表示单位矩阵,λ表示正则项系数.相应地,GK的伪逆计算可表示为:

2.4 增量学习层

针对BLS 模型达不到预期建模精度的问题,文献[31]提出了增加特征映射节点和增加特征增强层节点两种策略.本文的BHFR 以混合森林组为基本单元,依据训练误差的收敛程度实现增量学习,具体如下.

首先,对新数据集{X′,y}进行基于Bootstrap和RSM 的采样,获取混合森林算法训练子集,过程如下:

接着,构建第p个混合森林组中的决策树其过程与特征映射层和特征增量层相同,此处不再赘述.

进一步,当增加1 个混合森林组后,特征映射层、特征增量层和增量学习层的输出可表示如下:

式中,GK=[ZN|HK] 包含NRaw个样本和(2N+2K)维特征,GK+1包含NRaw个样本和(2N+2K+2J)维特征.

然后,进行GK+1的Moore-Penrose 逆矩阵的递推更新,如下:

式中,矩阵C和矩阵D的计算如下:

进而,GK+1的Moore-Penrose 逆矩阵的递推公式如下:

进一步,特征映射层、特征增量层和增量学习层与输出层间权重的更新矩阵为:

式中,WK=(λI+[GK]TGK)-1[GK]TY.

由于采用上述伪逆更新策略只需要计算增量学习层混合森林组的伪逆矩阵,因此能够实现快速的增量式学习.

进一步,根据训练误差的收敛程度实现自适应增量学习.此外,定义误差的收敛阈值θCon用以确定增量学习中混合森林组的数量p.相应地,BHFR模型的增量学习训练误差表示如下:

式中,ℓ表示增量学习第p+1 个与第p个混合森林组训练差值WK+p+1-y)2)1/2表示包含p个和p+1 个混合森林组的BHFR 模型训练误差.

最终,本文BHFR 模型的预测输出为:

2.5 算法伪代码

BHFR 方法的伪代码如下:

算法3.算法伪代码

由上述伪代码可知,特征映射层、特征增强层和增量学习层是在相同方向进行扩展,算法程序在实现上按照与建模策略相对应的描述进行编写,进而在软测量的工业应用中只需要通过更新增量学习层即可实现模型的在线更新.

3 实验研究与应用

3.1 实验数据和评价指标描述

本文先采用高维基准数据集验证,再采用北京某MSWI 电厂的实际DXN 数据进行工业验证,详细信息如表2 所示.

表2 实验数据统计结果Table 2 Statistical results of experimental datasets

表2 中,CT 切片数据集和住宅建筑数据集源自UCI 平台数据库[55];橙汁近红外光谱数据集源于http://www.ucl.ac.be;DXN 数据源自于北京某MSWI 电厂.本文数据在文献[23]的基础上进行了样本扩充和特征删减,共涵盖了2009～ 2020 年的DXN 排放浓度建模数据141 组.其中DXN 真值为2 小时采样化验后的折算浓度,每组建模数据的过程变量均为同一时刻下的过程数据,采样频率为小时,对缺失数据和异常变量进行剔除后的输入变量为116 维,其相应取值为当前DXN 真值采样时间段内的均值.

本文选取均方根误差、平均绝对误差和决定系数共三个评价指标比较不同方法的性能,计算如下:

3.2 基准验证

本文BHFR 方法的参数设置为: 决策树叶节点最小样本数Nsamples为7、RSM特征选择数量为决策树的数量Ntree为10、特征映射层和特征增强层中混合森林组的数量NForest均为10、正则化参数λ为 1-10.

首先,根据特征映射层的输出ZN和原始输入数据的全联接混合矩阵A确定用于特征增强层和增量学习层潜在特征数量.在NIR、CT 和RB 数据集中A的特征维数分别为900、491 和303 维,其前60 个潜在特征的累计贡献率如图4 所示.

根据图4 所示,当潜在特征贡献率阈值η为0.9 时,NIR、CT 和RB 数据集中选择的潜在特征数量分别为3、19 和12 个.上述所选潜在特征与真值间的互信息值如图5 所示.

图4 基准数据集中潜在特征的贡献率曲线Fig.4 Contribution rate curves of latent features of benchmark datasets

如图5 所示,互信息阈值ζ分别为0.70、0.85和0.80 时,NIR、CT 和RB 数据集中被选的潜在特征数量分别为2、11 和1 个.

图5 基准数据集潜在特征与真值的互信息值Fig.5 Mutual information values of latent features and true values of benchmark datasets

接着,预设增量学习层的混合森林组单元数量为100,BHFR 模型的训练误差与混合森林组数量间的关系如图6 所示.

由图6 所示的训练误差曲线可知,BHFR 在NIR、CT 和RB 数据集上的训练过程均可收敛至某一确定下限值.

图6 基准数据集训练误差收敛曲线Fig.6 Training error convergence curve of benchmark datasets

采用RF、DFR、DFR-clfc、BLS-NN 与本文方法进行对比,相应模型参数设置为:

1) RF,决策树叶节点最小样本数Nsamples为3,RSM 特征选择数量为,决策树数量Ntree为500;2) DFR,决策树叶节点最小样本数Nsamples为3,RSM 特征选择数量为,决策树数量Ntree为500,每层中RF 和CRF 模型的数量NRF和NCRF均为2,总层数设置为50;3) DFR-clfc,决策树叶节点最小样本数Nsamples为3,RSM 特征选择数量为,决策树数量Ntree为500,每层中R F 和CRF模型的数量NRF和NCRF均为2,总层数设置为50;4) BLS-NN,特征节点数Nm为5,增强节点数Ne为41,神经元数量Nn为9 和正则化参数λ为 2-30.

将上述方法在相同条件下重复20 次实验,其统计结果和预测曲线如表3～ 表5 和图7～ 图9 所示.

由表3～ 表5 和图7～ 图9 可知:

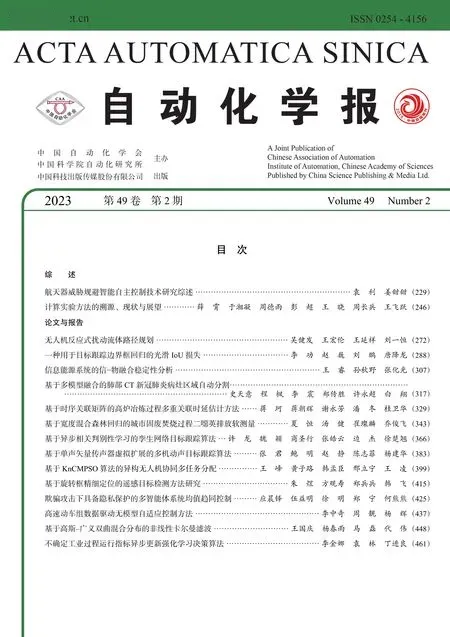
表3 NIR 数据集实验结果Table 3 Experimental results of NIR dataset

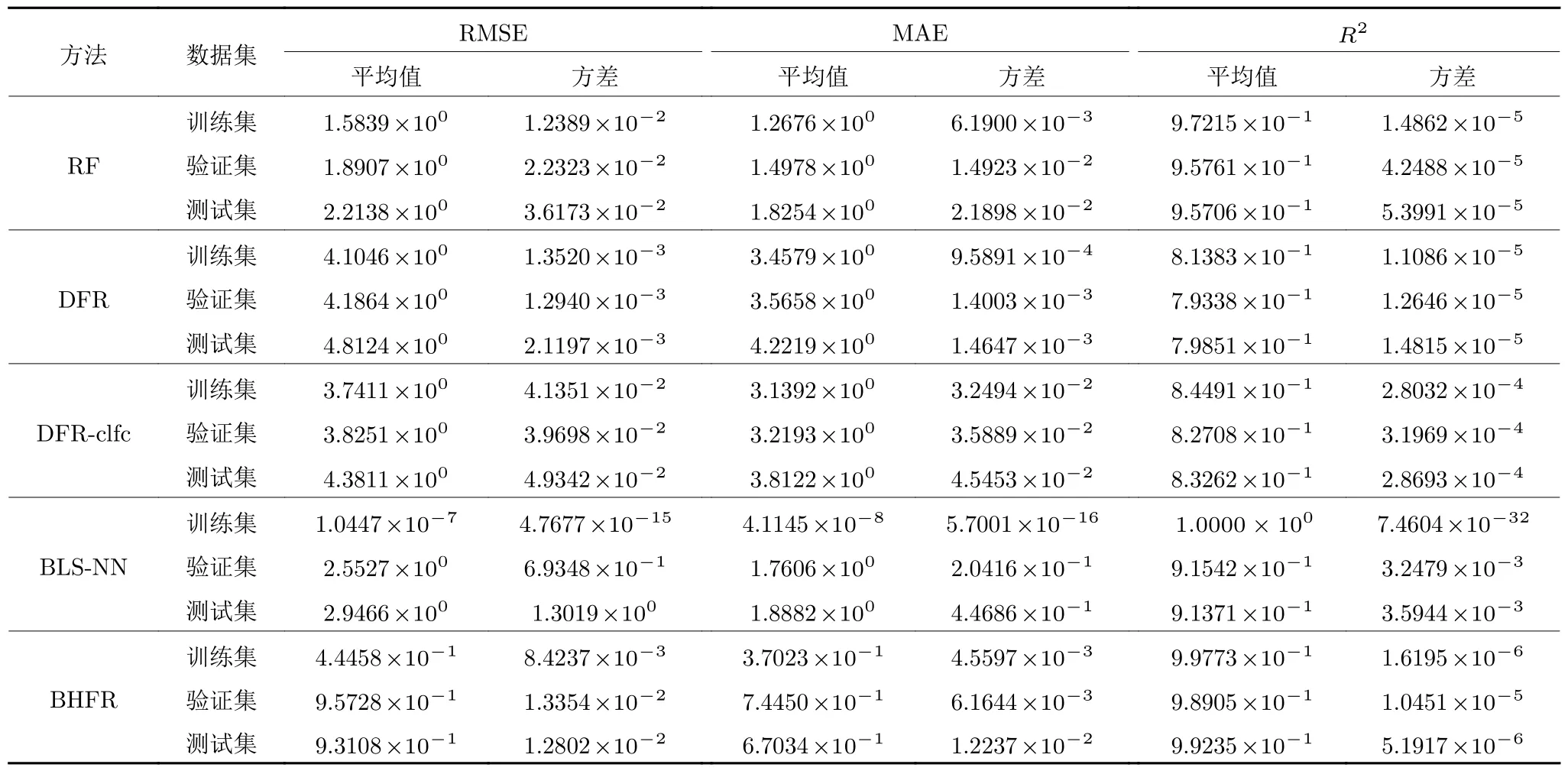
表4 CT 数据集实验结果Table 4 Experimental results of CT dataset

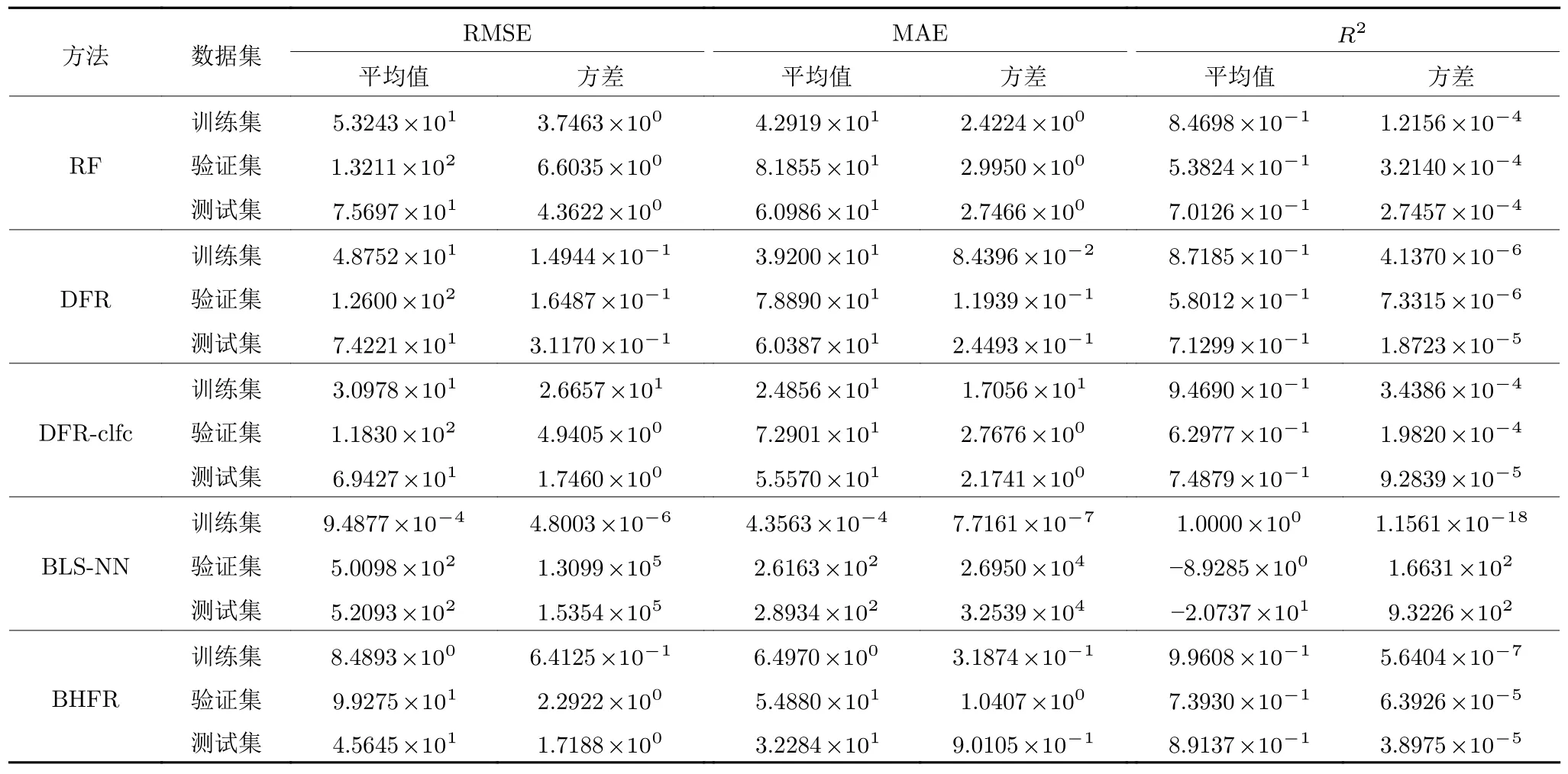
表5 RB 数据集实验结果Table 5 Experimental results of RB dataset

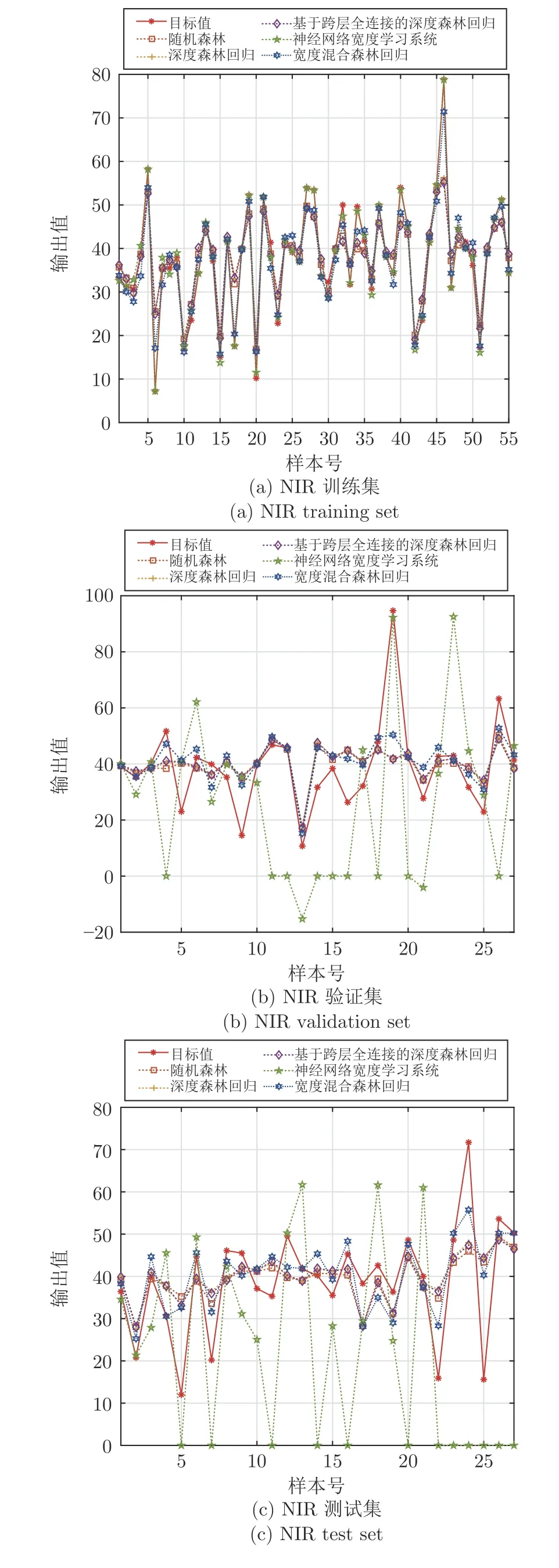
图7 NIR 数据集的拟合曲线Fig.7 Fitting curves of NIR dataset

图8 CT 数据集的拟合曲线Fig.8 Fitting curves of CT dataset

图9 RB 数据集的拟合曲线Fig.9 Fitting curves of RB dataset

1) NIR 数据集.在训练集中,RMSE、MAE 和R2指标的均值统计结果均以BLS-NN 最佳(7.4226×10-1、4.6530×1 0-1和9.9476×1 0-1),但方差统计结果弱于RF、DFR 和DFR-clfc,本文BHFR 在各项指标的均值和方差统计结果上的表现与BLSNN 接近;在验证集中,RF 的RMSE 和R2指标均值效果最佳(1.348×1 01和2.7181×1 0-1),DFRclfc 在3 个指标的方差统计结果最优,本文BHFR的性能整体不如RF、DFR 和DFR-clfc,BLS-NN在各项指标中表现最差;在测试集中,BHFR 在RMSE、MAE 和R2的均值统计结果优于其他方法,但其方差统计结果依旧低于RF、DFR 和DFRclfc;上述结果表明,BHFR 针对高维谱数据的泛化性能最强,但稳定性有待进一步增强.

2) CT 数据集.在训练集中,BLS-NN 的三个指标的均值和方差均表现最佳,BHFR 仅次于BLSNN,BHFR 的训练稳定性好于RF 和DFR-clfc;在验证集中,三个指标的均值统计结果均是本文BHFR 最佳(1.2459×1 00、8.5055×1 0-1和9.8148×10-1),其方差仅弱于DFR;在测试集中,BHFR 的表现与验证集一样,均值性能表现最佳,稳定性优于RF 和DFR-clfc,DFR 性能最稳定.上述结果表明: 相较于基于树的方法,BLS-NN 在训练时存在明显的过拟合现象;本文BHFR 的均值性能最佳,但其稳定性有待加强.

3) RB 数据集.训练集中,BLS-NN 的三个指标的均值和方差结果均为最佳;本文BHFR 的均值统计结果在验证和测试数据集中均优于其他方法,但BHFR 在模型稳定性方面依然弱于DFR 方法.上述结果表明,BLS-NN 存在过拟合,本文BHFR稳定性有待增强.

综上可知,上述小样本高维数据的实验结果表明了本文BHFR 具有比RF、DFR 及其改进版DFRclfc、BLS-NN 更佳的泛化性能.

3.3 工业验证

在DXN 数据集中,本文BHFR 的参数设置为:决策树叶节点最小样本数Nsamples为7,RSM特征选择数量为决策树的数量Ntree为10,特征映射层和特征增强层中混合森林组的数量NForest均为10,潜在特征贡献率阈值η为0.9,正则化参数λ为 2-10.

类似基准数据集,基于全联接混合矩阵A确定用于特征增强层和增量学习层的潜在特征数量,其维数为316 维,前80 个潜在特征的累计贡献率如图10 所示.

根据图10 所示,当潜在特征贡献率阈值η为0.9 时,DXN 数据集中选择的潜在特征数量为35 个.接着,计算35 个潜在特征与DXN 真值间的互信息值,结果如图11 所示.

图10 DXN 数据潜在特征的贡献率曲线Fig.10 Contribution rate curve of latent feature of DXN dataset

根据图11 所示,将互信息阈值ζ设置为0.75,DXN 数据集中被选的潜在特征数量为6 个.进一步,预设增量学习层的混合森林组单元数量为1 000,相应地BHFR 模型的训练误差与混合森林组数量间的关系如图12 所示.

图11 DXN 数据潜在特征与真值的互信息值Fig.11 Mutual information value of latent feature and true value of DXN dataset

由图12 所示的训练误差曲线可知,BHFR 在DXN 数据集上的训练过程可收敛至某一确定下限值.

图12 DXN 训练误差收敛曲线Fig.12 Convergence curves of DXN training error

然后,采用RF、DFR、DFR-clfc 和BLS-NN与本文BHFR 进行对比.参数设置为: 1) RF,决策树叶节点最小样本数Nsamples为3,RSM特征选择数量为,决策树的数量Ntree为500;2)DFR,决策树叶节点最小样本数Nsamples为3,RSM特征选择数量为,决策树的数量Ntree为500,每层中RF 和CRF 模型的数量NRF和NCRF均为2,总层数设置为50;3) DFR-clfc,决策树叶节点最小样本数Nsamples为3,RSM 特征选择数量为,决策树的数量Ntree为500,每层中RF 和CRF 模型的数量NRF和NCRF均为2,总层数设置为50;4) BLSNN,特征节点数Nm为5,增强节点数Ne为41,神经元数量Nn为9 和正则化参数λ为 2-30.上述方法在相同条件下重复20 次实验,其统计结果和预测曲线如表6 和图13 所示.

由表6 和图13 可知,1) RF 在训练、验证和测试中的RMSE、MAE 和R2指标均值统计结果均优于DFR,但在稳定性指标上弱于DFR;2) DFR 和DFR-clfc 在建模精度上与RF 接近,同时建模稳定性要好于RF,其中DFR-clfc 在训练、验证和测试集的精度略高于DFR,但DFR 的稳定性更好;3)BLS-NN 对训练数据出现了明显的过拟合,其在验证和测试集中的泛化性能和稳定性上均表现最差,表明BLS-NN 难以适用于本文中的真实工业过程的小样本高维数据;4) BHFR 在测试集中的RMSE、MAE 和R2指标的均值统计结果均为最佳,稳定性仅弱于DFR,表明BHFR 具有良好的泛化性能和稳定性.

图13 DXN 数据集中的拟合曲线Fig.13 Fit curves of DXN dataset

表6 DXN 数据集实验结果Table 6 Experimental results of DXN dataset

综上可知,DXN 软测量建模实验表明本文BHFR具有比经典RF、DFR 及其改进版DFR-clfc 更好的学习能力,同时在测试集上的建模精度和对数据的拟合程度也强于RF、DFR、DFR-clfc 和BLS-NN,体现了其在构建DXN 软测量模型中的明显优势.

3.4 算法时间复杂度分析

在RF、DFR、DFR-clfc 和BHFR 模型中采用的决策树算法均为二叉树,该类型决策树算法的时间复杂度可表示为 OTree(M ×N ×logN) (一个决策树模型的时间复杂度记为 OTree(#Tree)),其中M表示数据的维度,N表示数据的样本数量.下面仅考虑模型的主要结构部分,并给出了各模型的算法时间复杂度.

1) RF 的时间复杂度为:

式中,#Tree*=MRSM×N ×logN,Ntree表示RF的决策树数量(一个森林模型的时间复杂度记为ORF(#Forest)).

2) DFR 的时间复杂度为:

式中,NRF和NCRF表示每层中RF 模型和CRF 模型的数量,Layers表示DFR 模型的深度.

3) DFR-clfc 的时间复杂度为:

式中,#Forest*=#Forest×β,β为森林模型复杂度的系数,该系数由每层逐渐增加的特征数量决定.

4) BLS-NN 的时间复杂度可表示为:

式中,Nm表示特征节点数量,Ne表示增强节点数量,Nn表示每个节点中的神经元数量.

5)本文BHFR 的时间复杂度为:

式中,#Forest*=#Forest×α,α表示森林模型复杂度的系数且α＜1 (潜在特征提取层的降维作用使得特征增强层和增量学习层的输入特征维数显著减小).

由式(41)～ 式(45)可知,BHFR 的时间复杂度TBHFR要远小于传统深度集成方法DFR 和DFRclfc 的TDFR和TDFR-clfc,即相对于深度集成算法BHFR 在时间成本上具有明显优势.相较于BLS-NN方法的TBLS-NN,BHFR 的时间复杂度偏高,其主要原因在于混合森林组的时间复杂度 O (#Forest) 要高于单一神经元.因此,进一步的研究是考虑在不损失模型精度的情况下降低BHFR 的时间复杂度.

3.5 超参数敏感性分析

为进一步对本文BHFR 进行性能评估,本节对决策树叶节点最小样本数Nsamples、RSM 特征选择数量MRSM、决策树的数量Ntree、混合森林组的数量NForest、潜在特征贡献率阈值η、互信息阈值ζ和正则化参数λ等超参数进行敏感性分析,其设置区间如表7 所示.

表7 BHFR 超参数及其区间设置Table 7 Super parameters and interval setting of BHFR

实验中采用单因素分析策略,即每次仅将单一参数作为可变项,测试集的R2实验结果如图14 所示.

由图14 可知:

1)决策树叶节点最小样本数Nsamples.如图14(a)所示,其横坐标表示设置的叶节点最小样本数Nsamples(每个数据集的横坐标长度不同,设置区间详见表5),纵坐标表示模型的性能评价指标R2.随着Nsamples的逐渐增大,NIR、RB 和DXN 数据集中的R2逐渐变小,表明取相对小的Nsamples时模型的泛化性能更佳,反之则较差;在CT 数据集中,模型性能不受Nsamples变化的影响,即当决策树仅包含一个根节点时(即Nsamples等于训练样本数量),测试集具有非常好的泛化性能.可知,不同数据集对BHFR 模型中Nsamples的敏感程度具有差异性.因此,将Nsamples设置在[3,10]最为合适.

2) RSM 特征选择数量MRSM.如图14(b)所示,其横坐标表示设置的RSM 特征选择数量MRSM(每个数据集的横坐标长度不同,设置区间详见表5),纵坐标表示模型的性能评价指标R2.当MRSM增加时,CT 和RB 数据集中的R2逐渐变大后保持平稳,NIR 和DXN 数据集中的R2曲线却具有明显的震荡趋势.可知,NIR 和DXN 数据集对MRSM的数量更为敏感,CT 和RB 数据集只需选取较少特征即可建立较高精度的模型,即数据间存在差异性.因此,将MRSM设置为原始特征数量的1/10,可兼顾模型的时间成本和泛化性能.

3)决策树的数量Ntree.如图14(c)所示,其横坐标表示设置的决策树的数量Ntree(每个数据集的横坐标长度均为5～ 100),纵坐标表示模型的性能评价指标R2.随着Ntree的逐步增加,CT、RB 和DXN 数据集中的R2趋势总体平稳,NIR 数据集中的R2的变化却较为明显.可知,针对CT、RB 和DXN数据集,决策树数量对模型的影响较小,选取较少的决策树建模即可保证模型性能.因此,将Ntree设置为40,可使模型适用于不同数据集的建模需求.

4)混合森林组的数量NForest.如图14(d)所示,其横坐标表示设置的混合森林组的数量NForest(每个数据集的横坐标长度均为5～ 100),纵坐标表示模型的性能评价指标R2.随着NForest的增加,各数据集的性能表现与超参数Ntree相一致.可知,NForest的设置不宜过大,其值适当时模型的泛化性能最佳.因此,将NForest设置在[25,35]区间,模型建模精度较高.

5)潜在特征贡献率阈值η.如图14(e)所示,其横坐标表示设置的潜在特征贡献率阈值η(每个数据集的横坐标长度不同,设置区间详见表5),纵坐标表示模型的性能评价指标R2.其决定着从全联接混合矩阵特征空间A中提取的潜在特征数量,η越大表示潜在特征维数越高.实验表明,随着η增大,CT 数据集中的R2表现最稳定,NIR、RB 和DXN数据集中的R2在接近η=1 时,出现局部最小值(即模型性能最差).可知,本文方法对超参数η的敏感程度相对较低.因此,将η设置为0.9,可确保选择合适数量的潜在特征,进而保证建模精度.

6)互信息阈值ζ.如图14(f)所示,其横坐标表示设置的互信息阈值ζ(每个数据集的横坐标长度不同,设置区间详见表5),纵坐标表示模型的性能评价指标R2.理论上其决定特征增强层和增量学习层的输入特征维数,ζ越大表示输入特征维数越低.实验中,随着η增大,CT 数据集的性能不变,RB数据集的R2存在极小值,DXN 数据集的R2先变大后平稳,NIR 数据集的R2逐渐变小后接近稳定.可知,CT 和DXN 数据集,超参数ζ对模型性能的影响较小;但RB 和NIR 数据集,超参数ζ设置较小时模型性能更佳.因此,综合不同数据集的结果可知,将ζ设置为0.7 较为合适.

图14 超参数敏感性分析曲线Fig.14 Sensitivity analysis curves of super parameter

7)正则化参数λ.如图14(g)所示,其横坐标表示设置的正则化参数λ(每个数据集的横坐标长度不同,设置区间详见表5),纵坐标表示模型的性能评价指标R2.随着λ逐渐变小,NIR、CT、RB 和DXN 数据集的总体表现为先逐渐增大再达到稳定,其中RB 数据集在模型达到平稳后表现出明显的震荡现象.可知,正则化参数λ对不同数据集的影响是一致的,其中以RB 数据集最为敏感.因此,将λ设置为 1-10可使模型效果达到最佳.

综上可知,不同超参数针对不同数据集具有差异性,有必要进行全局优化.

4 结论

针对MSWI 过程关键指标参数DXN 排放浓度难以实时准确检测的问题,本文提出了一种基于BHFR 的软测量方法,其结合了宽度学习、集成学习和潜在特征提取等算法,主要贡献: 1)基于宽度学习系统框架,采用非微分学习器构建了包含特征映射层、潜在特征提取层、特征增强层和增量学习层的软测量模型;2)利用信息全联接、潜在特征提取和互信息度量对BHFR 模型内部信息进行处理,有效保证了BHFR 模型内部特征信息的传递最大化和冗余度最小化;3)采用混合森林组为映射单元实现建模过程的增量学习,通过伪逆策略快速计算输出层权重矩阵,再利用训练误差的收敛程度自适应调整增量学习,实现了高精度的软测量建模.基于北京某MSWI 电厂的真实数据验证了DXN 浓度软测量模型的有效性.

今后的研究工作是进行基于数值仿真的机理分析,实现面向生成、吸附和排放等多阶段的DXN 排放浓度软测量建模,为MSWI 过程污染排放运行优化控制提供有效支撑.