INS/GNSS/VO组合导航系统复合型异常检测与容错算法

胡晓强，武东杰，彭侠夫

（1.温州大学 电气与电子工程学院,温州 325035；2.厦门大学 航空航天学院,厦门 361101）

随着人类活动空间的不断扩展，上到卫星、火箭、飞机，下到汽车、轮船、潜器，各式各样的载体在人类的生产生活中得到了广泛的应用。导航系统为载体提供精确的位置、速度和姿态信息，是载体实现姿态控制、轨迹跟踪、自主巡航等功能的基础。惯性导航系统（Inertial Navigation System,INS）可以提供高频率、全维度的自主导航信息，常常作为主导航系统。其他导航系统提供辅助导航信息，以抑制惯性导航系统由于元件误差的累积而产生的漂移问题[1,2]。组合导航技术提高了导航系统的精度与应用范围，但辅助导航系统的使用也为其带来了新的问题，异常的辅助导航信息将使组合导航系统的输出偏离正常范围，甚至完全发散而无法使用。因此，组合导航系统的异常检测与容错成为现今导航领域的一大关键问题。

相比于其他领域，组合导航系统的异常检测问题具有其独有的特点：1）输出的动态性，组合导航系统在三维空间中做六自由度的运动，其传感器输出的导航参数并不会围绕若干个固定数值上下波动，因此构造残差数据成为导航系统异常检测所必须的预先操作；2）模型的简单性，组合导航系统的异常检测并不涉及具体的硬件结构，仅关注于传感器的输出参数，因此其本质上是一种数据的异常监测技术[3]。

惯性导航系统可以通过测量单元的冗余配置保证其完好性[4]。假设惯性导航系统正常工作，组合导航系统的异常检测算法常使用滤波算法的相关变量构建残差数据。残差卡方检测法通过滤波器的量测残差构建检测统计量，对幅值较大的突变型异常信号和快速增长的斜坡型异常信号具有良好的诊断效果，是一种经典的异常检测方法[5,6]。针对残差卡方检测法对缓变型异常信号检测不灵敏的问题，一些学者引入序贯滤波的思想，提出了渐消序贯概率比检验方法[7]。

随着人工智能的发展，基于知识的智能算法被引入到基于滤波残差的异常检测算法之中。其中，启发式算法的知识源于专家经验，其异常检测性能取决于规则的丰富程度与专家知识的准确性，对未建模的异常具有一定的局限性[8,9]。解析式算法通过残差的历史数据获取辅助导航系统的正常模式和异常模式，又被称为基于数据驱动的异常检测方法[10-12]。然而，带标签的异常数据获取难度大和检测模型可移植性差，制约了智能算法在现实中的使用与推广。卡方检测法仍然是导航系统中最常用的一种异常检测算法。

基于滤波器残差的异常检测算法，其性能受到故障跟踪效应或者滤波器方差增大问题的影响。为了避免故障跟踪效应的影响，增强残差诊断算法的异常检测能力，一些学者使用回归模型训练辅助导航系统的预测模型，以预测输出为基准获取残差数据[13-15]。在子系统短时失效的情况下，基于回归模型的异常检测算法可以使用预测值替代辅助导航系统的输出值，保证导航滤波器的稳定性。但是，在辅助导航系统长期失效或者载体做高机动运动的情况下，导航参数的预测模型具有一定的局限性。

实际中，导航系统的异常输出常由外部环境的干扰引起，表现为幅值较小的突变信号或者增长速率较慢的斜坡信号。上述异常检测算法对该种异常信号的监测能力较弱，故障跟踪效应更是加剧了异常信号在漏检之后的再检难度[16]。因此，在隔离异常子系统或异常观测量之外，一些学者采用异常检测结果构造权重系数对组合导航系统进行容错滤波。王融等[17]使用序贯概率比法评估滤波器状态，并使用评估结果修正状态估计的方差。Li T 等[18]对滤波器的标准化残差分量进行双阈值判定，构造测量噪声方差的权重因子。上述两个算法都忽视了各个导航滤波器之间异常检测结果的相关性。Xu J 等[19]使用双-状态卡方检测法计算状态的检测统计量，并以此设计向量式动态新息分配系数法，构造量测噪声的权重向量与联邦滤波器的动态信息分配系数。但是，动态的信息分配系数并不适用于观测数据长时间存在异常的情况。

为了增强异常检测算法对异常信号的监测能力，提高组合导航系统的导航精度，本文提出一种复合型异常检测与容错滤波算法，对滤波子系统的异常检测结果进行综合分析以增加异常数据与正常数据之间的差异；设置阈值比下界以改善量测噪声矩阵的调整策略；采用固定系数取代动态信息分配方案以增强导航系统在长时间输出异常下的稳定性；结合非全局融合阶段的异常检测隔离与全局融合阶段的加权容错滤波，实现组合导航系统的信息融合优化。

1 INS/GNSS/VO组合导航系统

1.1 卡尔曼滤波模型

以东北天坐标系为导航参考坐标系，右前上坐标系为载体坐标系。以惯性导航系统的误差模型作为滤波模型，系统的状态向量为：

滤波器的系统状态方程为：

系统的观测方程为：

式中，Zk为INS 与其他导航系统的三维位置误差；Hk为系统的观测矩阵；wk为量测噪声矩阵，其各元素服从零均值高斯分布。

1.2 局部更新与全局融合

第i个滤波子系统的时间更新为：

第i个滤波子系统的量测更新为：

式中，Ki,k为子系统i在k时刻的滤波器增益系数矩阵；Hi,k为子系统i在k时刻的观测矩阵；为子系统i在k时刻的系统量测噪声协方差矩阵；wi,k为子系统i在k时刻的量测噪声向量；Zi,k为子系统i在k时刻的观测向量。

联邦滤波器如图1所示，其全局状态估计为：

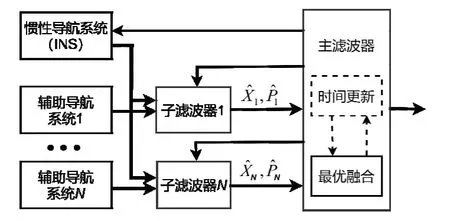
图1 联邦滤波器的结构Fig.1 Structure of federated filter

其信息分配过程为[19]：

式中，βi为子滤波器的信息分配系数，满足：

2 异常检测与容错算法

2.1 状态卡方检测法

状态卡方检测法通过比较状态递推器(只有时间更新的滤波器)与导航滤波器的状态估计差异实现组合导航系统的异常检测。状态递推器在k时刻的状态估计值为，导航滤波器i在k时刻的状态估计值为，若状态向量在k时刻的真实值为，则对应的估计误差分别为两个估计误差的差值为其协方差为：

在较短的时间内忽略量测更新的影响，可以假设滤波器残差向量r在正常情况与异常情况分别服从如下的正态分布：

正常状态Sn：；

异常状态Sf：。

构造r在两个分布下的对数似然比：

求u的导数并令，得到u的极大似然估计为u=r，对应的极大似然估计值为：

去除式(11)中的常值系数，得异常检测函数为：

在辅助导航信息正常情况，检测统计量fD服从自由度为n的卡方分布，即fD～χ2(n)。给定虚警率Pnf，就可由χ2(n)分布确定异常检测阈值TD。若fD＞TD，则判定辅助导航系统中存在异常输出。

2.2 归一化阈值比异常检测与容错算法

状态卡方检测法通过对比状态递推器与滤波子系统的差异，构造残差数据进行辅助导航系统的异常检测。但是，忽视不同滤波子系统异常检测结果之间的关联性，容易导致错误的容错处理。针对上述问题，本文设计了一种基于联邦滤波器的归一化阈值比异常检测与容错方法（Normalized Threshold Ratio-based Anomaly Detection and Tolerant Method,NTR-ADM），当辅助导航系统的观测信息输入滤波子系统时，对输入信息进行异常检测、分离和容错，整个量测更新过程如图2所示。

图2 异常检测与容错算法流程图Fig.2 Flow chart of anomaly detection and fault tolerance algorithm

首先，使用时间更新后的导航滤波器i构建相应的临时滤波器i，并直接使用观测向量对临时滤波器i进行量测更新：

对比临时滤波器与状态递推器的差异构建状态卡方检测量：

在惯性元件精度较低的场合，为了避免状态递推器长期缺乏量测更新而导致的状态卡方检测法异常检测性能急剧衰退，本文使用单一的状态递推器以获得更小的递推器重置周期。设置递推器的重置周期TRe，在周期结束时重置递推器的状态估计方差：

在联邦滤波器的全局融合阶段，构建检测统计量的归一化阈值比。为了避免量测噪声矩阵在导航信息正常时的错误调整，增强滤波系统的稳定性，在构建阈值比的过程中设置阈值比下界：

使用归一化阈值比作为量测噪声方差阵的权重系数，对联邦滤波系统进行容错滤波：

其次，为了避免导航参数长时间异常情况下异常状态的方差大幅度增加而导致的检测性能震荡问题，NTR-ADM 去除了向量式动态信息分配法(Vector-Form Dynamic Information Sharing Algorithm,VF-DIS)[19]的动态信息分配方案，使用式(7)对滤波子系统进行信息分配，并使用闭环修正后全局滤波器的状态估计结果重置状态递推器状态：

最后，在非全局融合阶段，使用状态卡方检测法的检测阈值TD,s对观测分量进行异常检测，并在子滤波器的量测更新中去除异常的观测信息，以保证组合导航系统在非全局融合阶段的稳定性。对照实验表明，全局融合阶段与非全局融合阶段采用不同的检测阈值，有利于提高组合导航系统的定位精度。

3 实验验证

3.1 硬件设备与实验设置

以INS/GNSS/VO组合导航系统为对象，验证本文算法的可行性。实验所用的无人车与导航设备如图 3所示，设备参数如表1所示。

表1 导航设备参数信息Tab.1 Parameters of navigation devices

图3 车载导航系统Fig.3 Vehicle navigation system

以实时动态差分系统（Real-time kinematic,RTK）的定位结果为参考基准。如图4所示，小车轨迹全长约1500 m，大致用时1200 s。载体的初始姿态为[0° 0° 90°]；全局坐标系采用地心惯性坐标系，全局初始位置Pg,0由RTK 提供，为北纬24.6109 °、东经118.3071 °与海拔29.1697 m；局部坐标系以小车的起始点为原点，采用东北天坐标系，局部初始位置PL,0设置为[0，0，0]（单位：m）；初速度为0 m/s。初始姿态误差标准差设置为[1° 1° 5° ]；初始速度误差标准差为0 m/s。通过对照实验，GNSS 与VO 位置观测误差的标准差分别设置为[0.7 0.7 1]与[1 1 1]（单位：m）。VO 采用视觉惯性导航系统(Visual-Inertial Navigation Systems,VINS)[20]的双目视觉模式获得小车的相对位置，再通过RTK 提供的初始位置PG,0将数据转化为地固坐标系下的纬度、经度与高度数据；GNSS 提供单点全局定位数据（纬度、经度与高度）。考虑到惯性器件误差参数影响较大，实验中INS、GNSS 与VO 中心点之间的空间位移小于40 cm，忽略导航系统间的杠臂效应，以两个辅助导航系统的全局定位数据作为组合导航系统的观测输入。以RTK 提供的定位结果为参考基准，辅助导航系统在局部坐标系下的位置误差曲线如图5所示。由于道路两旁树木的遮挡还有教学楼的影响，GNSS 的位置参数上存在着一定的导航误差。而由于VO 的误差累积问题与姿态估计误差，VO 的位置信息上存在着振荡的定位误差。两种误差使GNSS 与VO 的导航参数偏离了正常的数值范围，即其导航输出中包含有一定的异常信息。

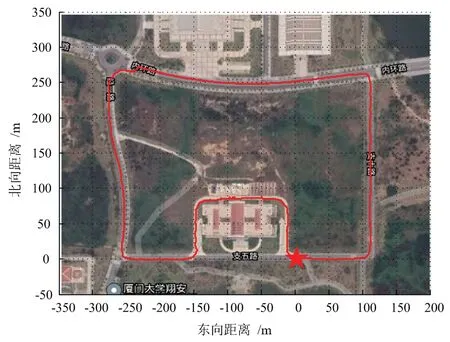
图4 实验轨迹的平面图Fig.4 Plane image of experimental trajectory

图5 GNSS 与VO 的位置误差Fig.5 Position errors of GNSS and VO

3.2 参数灵敏度分析

在基于滤波器残差的组合导航系统异常检测算法中，异常检测结果影响滤波器的量测更新过程，而异常检测结果又反过来受到滤波器状态的影响，两者之间的作用是相互耦合的。组合导航系统的定位精度受到异常检测的参数设置、异常输出的数值与持续时间、INS 的误差累积速度等因素的共同影响，难以通过理论分析确定参数设置对 NTR-ADM 性能影响。NTR-ADM 具有三个参数：阈值比值下界L，状态卡方检测阈值TD,s与全局融合阶段的检测阈值TD,g。为了可视化数值分析结果，固定一个参数的数值后设置剩余两个参数的对照实验，分析参数设置对NTR-ADM容错性能的影响。

首先，固定TD,s= 5，在0.5 到8 的范围内，以0.5为间隔，设置TD,g的对照组；在1 到5 的范围内，以1 为间隔，设置下界L的对照组。实验结果如图6(a)所示，在不同参数设置下，轨迹上各点的导航误差均值在4.194 m 到6.477 m 的范围内上下波动。以导航误差均值最小为指标，存在两条容错性能比较良好且稳定的参数带（图中的灰色部分）。其中，当(TD,g,L) =（7.5,1）时，NTR-ADM 各点的导航误差均值为4.194 m，达到对照实验组的最小值。

基于上一组对照实验的结果，固定L= 1，在0.5到8 的范围内，以0.5 为间隔，设置TD,g的对照组；在3 到7 的范围内，以1 为间隔，设置TD,s的对照组。实验结果如图6(b)所示，在不同的诊断参数设置下，轨迹上各点的导航误差均值在3.081 m 到8.513 m 的范围内上下波动。以导航误差均值最小为指标，存在两个容错性能比较良好且稳定的参数区间（图中的灰色部分）。其中，当(TD,g,TD,s)= (7.5,3)或者(8,3)时，NTR-ADM 各点的导航误差均值为3.096 m，达到对照实验组的最小值。

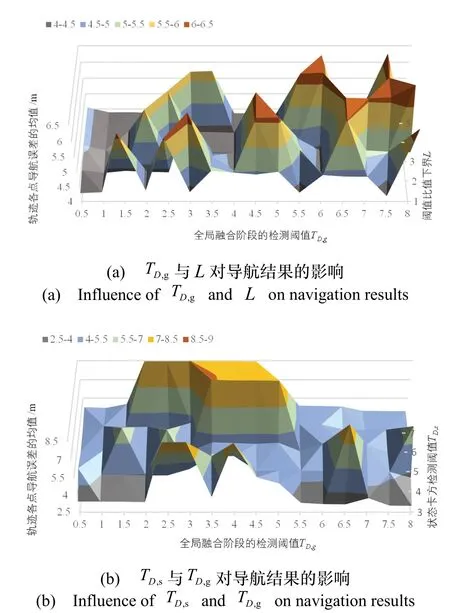
图6 NTR-ADM 的参数灵敏度分析Fig.6 Parameter sensitivity analysis for NTR-ADM

综上所述，针对使用中等精度惯性器件的INS/GNSS/VO组合导航系统，NTR-ADM 对其参数设置具有一定的鲁棒性，能在一定的参数区间内维持较为良好与稳定的容错性能。

3.3 算法对比

选取如下算法作为NTR-ADM 的对比算法：1）无诊断模式（None-Diagnosis Model,NDM），直接融合所有的传感器数据；2）残差卡方检测法（Residual Chi-Square Test,RCST），使用观测量预测误差构建观测分量的异常检测量；3）状态卡方检测法（State Chi-Square Test,SCST），使用状态预测误差构建观测分量的异常检测量；4）基于新息的异常点消除算法（Innovation-Based Outlier-Resistant Ambiguity Resolution,IO-RAR）[18]，使用标准化残差数据集与两个检测阈值构建量测噪声方差的权重系数；5）向量式动态信息分配法（Vector-Form Dynamic Information Sharing Algorithm,VF-DIS）[19]，使用双状态卡方检测量与检测阈值构建量测噪声协方差矩阵的权重系数与信息分配系数。

其中，RCST 与SCST 都增加了“综合容错策略”以抑制INS 的发散：当GNSS 与VO 的某一观测量都被判定为异常数据时，保留该分量进行量测更新。为了防止VF-DIS 发散，在求取fD,(i,j)与检测阈值的比值时，增加了比值下界L= 1。以轨迹上各点的导航误差均值最小为目标，在不同的检测阈值下，设置各个算法的对照实验，确定算法的最优参数，结果如表2所示。其中，NTR-ADM 使用参数灵敏度分析试验中的最优参数设置，即TD,s= 3，TD,g=7.5，L= 1。

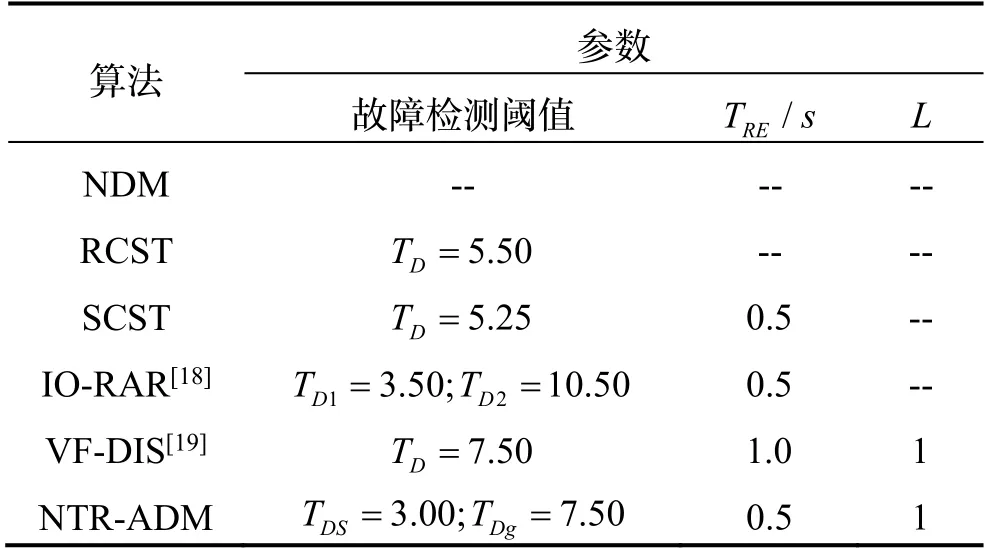
表2 故障诊断算法的参数设置Tab.2 Parameter setting of fault diagnosis algorithm

3.3.1 导航误差分析

轨迹上各点导航误差的统计结果如图7所示。由图7 中可以看出：

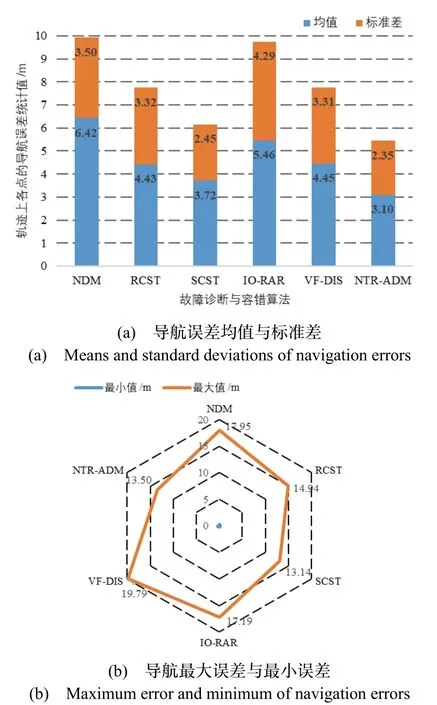
图7 各算法的导航误差统计结果Fig.7 navigation error statistics of the algorithms

1）在参数合理设置情况下，各算法的导航结果均优于NDM，轨迹上各点的导航误差均值较NDM 分别减小了31.1%，42.2%，15.0%，30.8%与51.8%；

2）除了IO-RAR 的误差标准差与VF-DIS 的误差最大值，各算法误差的变化范围均小于NDM；

3）NTR-ADM 各点的导航误差最大值、均值、标准差分别为13.5 m、3.10 m、2.35 m，相对于NDM 分别减小了24.8%、51.8%与32.7%。六种异常检测与容错算法中，NTR-ADM 的导航误差最大值为次小（最小为SCST 的13.14 m，相对于NDM 减小了26.8%）；NTR-ADM 的误差均值为最小，相对于次小的SCST（3.72 m，相对于NDM 减小了42.2%）减小了9.6%；NTR-ADM 的标准差为最小，相对于次小的SCST（2.45 m，相对于NDM 减小了30.0%）减小了2.7%，获得了最优的导航结果。

3.3.2 异常检测结果分析

在联邦滤波结构的组合导航系统中，前一时刻的异常检测与容错结果，将会影响后一时刻的异常检测过程。根据上一小节的导航误差分析结果，选取SCST、VF-DIS 与NTR-ADM 算法进行异常检测结果分析。

三种算法中位置状态分量的异常检测结果与导航误差曲线分别如图8-9所示，其中，检测统计量1-3分别对应于导航滤波器中载体纬度、经度与高度误差的检测统计结果。由图中数据可以看出：

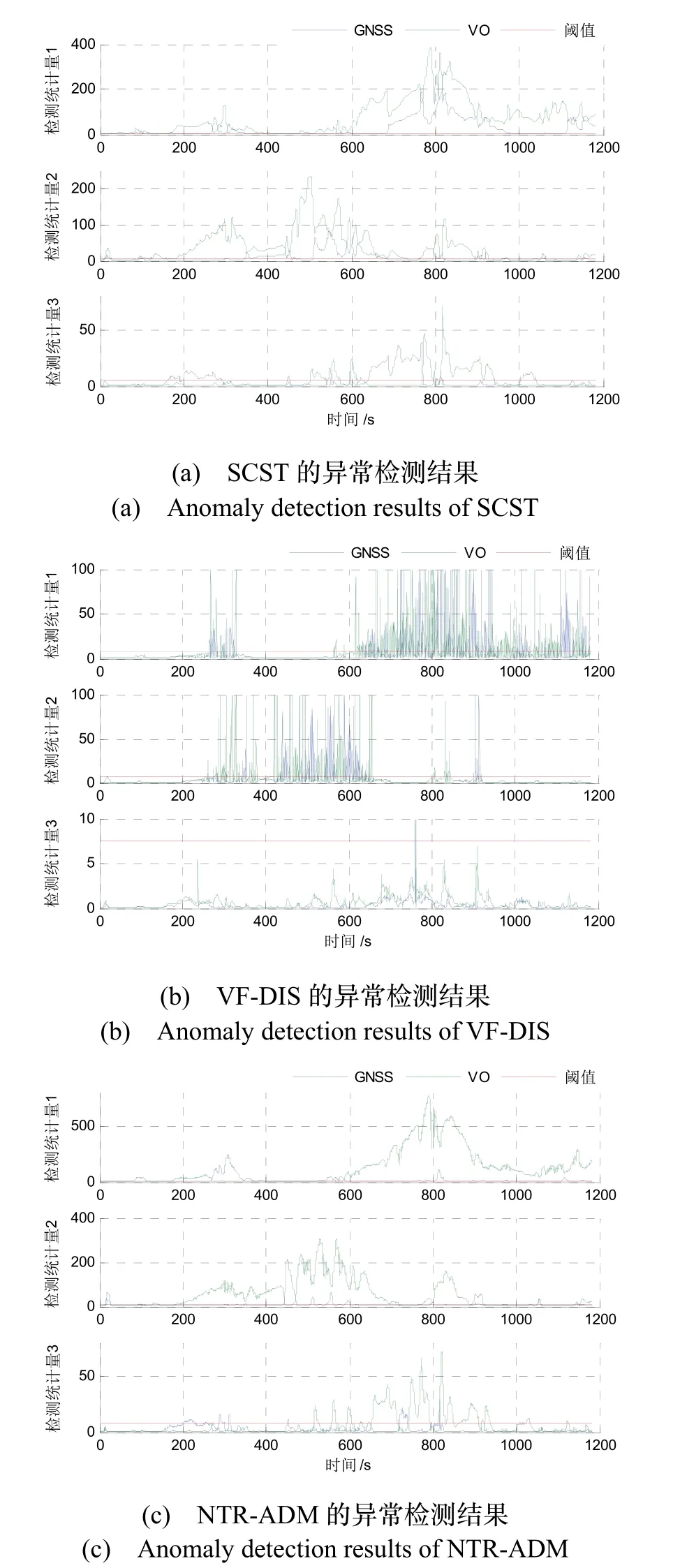
图8 各算法的异常检测结果Fig.8 Anomaly detection results of the algorithms

1) SCST、VF-DIS 与NTR-ADM 对高度误差的诊断结果都不够准确。由图5 可以看出，由于外部环境扰动或者本身算法的误差累积，GNSS 与VO 的高度输出上都长期存在着大约2～4 m 的误差数据（其中GNSS 的误差较大），造成高度输出异常。SCST 检测出了650～800 s 的GNSS 输出异常与800～950 s 的VO输出异常；VF-DIS 几乎没有检测出任何的高度输出异常；本文的NTR-ADM 检测出了650～950 s 的VO 输出异常。

基于上述的异常检测结果，在650～950 s 上，SCST与NTR-ADM 的高度误差较大且上下波动；而VF-DIS的高度误差波动较小。

2) NTR-ADM 对于水平误差的诊断结果优于SCST 与VF-DIS。由图5 的数据分析可以看出，由于误差累积与姿态估算误差，VO 在纬度与高度输出上存在着较大的误差，造成VO 的水平输出异常。SCST检测出了VO 在600～1200 s 上的纬度输出异常与200～700 s 上的经度输出异常，但也将GNSS 数据大量误检为异常数据。VF-DIS 的检测统计量上下波动十分剧烈，检测出了VO 在600～1200 s 上的纬度输出异常与300～340 s、355～380 s 上的经度输出异常，但检测区间上伴随着大量的GNSS 误检。使用单递推器的NTR-ADM，避免了异常检测曲线的剧烈波动，不仅检测出了VO 在600～1200 s 上的纬度输出异常与200～700 s 上的经度输出异常，对GNSS 还具有更小的误检率，仅在有限的区域（例如270～350 s 的纬度数据、450～470 s 的经度数据）上出现了GNSS 的误检与VO 的漏检。

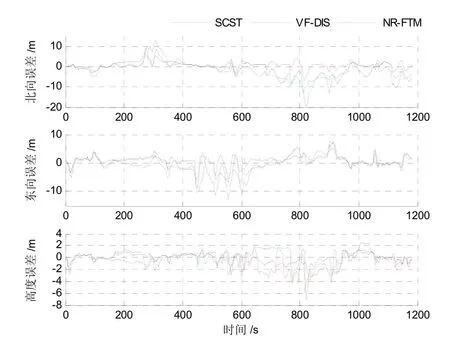
图9 各算法的导航误差曲线Fig.9 Navigation error curves of the algorithms

在“综合容错策略”下，GNSS 的误检数据与VO的异常数据将同时用于量测更新。基于上述异常检测结果，SCST 在700～950 s 上具有较大的纬度误差，在450～600 s 上具有一定的经度误差波动；VF-DIS 的水平误差分布与SCST 相似，但变化幅度更大；而NTR-ADM 仅在260～350 s 上具有较大的纬度误差，在440～600 s 上的经度误差波动也较小。

4 结论

为了提高INS/GNSS/VO组合导航系统在外部扰动下的定位精度，提出一种复合型异常检测与容错滤波算法（NTR-ADM）：在非全局融合阶段，使用状态卡方检测法进行异常数据的检测与隔离；在全局融合阶段，使用检测统计量构建量测噪声方差的加权系数，实现系统的容错滤波。

相对于改进前的VF-DIS，阈值比例下界的设置，防止了系统在正常情况下对量测方差进行错误的加权调整；归一化的检测阈值比，提高了松组合系统的导航精度；单状态递推器缩小了递推器重置周期，避免了异常检测曲线在低精度惯性器件下的剧烈波动。街道场景下小车的离线实验表明，NTR-ADM 各点的导航误差均值与标准差相对于无容错情况分别减小了51.8%与32.7%，相对于其他异常检测与容错算法至少分别减小了9.6%与2.7%，为各方案中的最优。