A robust filter for tightly coupled MEMS-INS/GPS integrated navigation in an urban environment

HE Tao ,ZHANG Huijun,LI Xiaohui,JIANG Nan,WANG Dongyu

(1.National Time Service Center,Chinese Academy of Sciences,Xi’an 710600,China;2.Key Laboratory of Precision Navigation and Timing Technology,National Time Service Center,Chinese Academy of Sciences,Xi′an 710600,China;3.University of Chinese Academy of Sciences,Beijing 100049,China;4.Kunming Shipborne Equipment Research and Test Center,China State Shipbuilding Corporation Limited,Kunming 650051,China)

Abstract:A robust filter model based on Kalman filter,named rubust Kalman filter (RFK),is proposed to improve the performance of tightly coupled MEMS-INS/GPS integrated navigation system in urban areas with the GPS signal challenge of short outages or disturbances.In the RKF procedure,the Kalman filter (Kalman filter,KF) with error detection and isolation (error detection and isolation,EDI) is constructed to overcome the challenge of abrupt faults in GPS measurements including pseudorange and pseudorange rate,then adjusts the GPS measurement noise by adaptive factor vector for high navigation solution.Then the field experiment is carried out on an urban road to test the availability of the RKF.Compared with the traditional KF,the horizon position errors decrease by over 30%,while the errors reduction on height position are approximately 50%with RFK,and the velocity errors are decreased by 17.5%.RFK can effectively reduce the navigation solution errors of tightly coupled MEMS-INS/GPS integrated navigation system in urban areas.

Key words:robust filter;error detection and isolation;adaptive filtering;tightly coupled;Urban environment;GPS

Combining the advantages of the global navigation satellite system (GNSS) and inertial navigation system(inertial navigation system,INS),the INS/GNSS integrated navigation system has been widely used in various scenarios.The main architectures of integrated navigation include loosely coupled (loosely coupled,LC)and tightly coupled (tightly coupled,TC) systems.For the same hardware,the TC architecture performs better than the LC architecture in terms of accuracy and robustness because the correlated measurements that arise due to cascaded Kalman filtering in the LC approach are eliminated;moreover,GNSS updates continue even if fewer than four satellites are visible,so the TC architecture is selected as the study case in this paper.Microelectromechanical system (MEMS) INSs with small sizes and low costs are integrated with GNSS receivers for cost-effective integrated navigation systems,although ramp errors may be introduced to navigation solutions in dense urban areas[1],where GNSS signals are challenged by short outages,multipath delays and interference because of buildings or obstacles around integrated navigation equipment[2,3].For land vehicles,slope and turning on urban roads may lead to changes in the motion state,which may impair the accuracy of navigation solutions.

In recent decades,error detection and isolation (EDI)has been investigated to eliminate GNSS abnormal data and obtain an accurate navigation solution when MEMSINS/GNSS works in urban areas.Yang (2014) described an enhanced quality control algorithm for use with a MEMS-INS/GNSS integrated navigation system to reduce the INS slowly growing error during GNSS outages and mitigate the effect of abrupt errors caused by GNSS multipath[4].Li (2017) made full use of a satellite selection algorithm to select an optimal satellite combination and eliminate the abnormal GNSS satellite measurement data for positioning accuracy in INS/GNSS tightly coupled systems[5].Wang (2022) proposed threedimensional light detection and ranging-based real-time fault detection and localization algorithms to achieve a high-precision and robust integrated system[6].In addition,other sensors,such as odometers,barometric altimeters and chip-scale atomic clocks (CSAC),can be integrated into navigation systems for reliable solutions in complex urban environments[7-9].Li (2018) used an atomic clock and barometric altimeter together to improve positioning accuracy and continuity[10].Lai (2020) reported a multisensor tight fusion (MTF) method systematically fusing the GNSS,INS,odometer,barometric,and clock model for vehicle navigation in urban environments[11].Han(2022) proposed a factor graph optimization algorithm of GNSS/INS with gross error online detection to improve the performance of the integrated navigation system under the interference condition of urban environment[12].

Moreover,the variance of measurement noise properties in urban areas due to GNSS partly denial or the urban road condition,such as turning or slope,also have a great influence on the performance of MEMS-INS/GNSS integrated navigation.Consequently,a series of adaptive Kalman filtering (AKF) algorithms have been constructed in recent years to address this problem.Yu (2012)employed an adaptive filter that can estimate measurement noise variance using the residual of the measurement for a better accuracy of position and attitude error estimation[13].Sun (2022) proposed an improved innovation adaptive Kalman filter (IAKF) to solve the vulnerability of Kalman filtering in challenging urban environments during integrated navigation[14].

To address the challenge in urban environments,GPS and MEMS-INS are selected to construct an integrated navigation system as study case,and a Kalman filterbased model named robust Kalman filter (robust Kalman filter,RKF),which combines the advantages of EDI and AKF,is presented in this paper for the reliable and accurate navigation solution of TC MEMS-INS/GPS integrated navigation systems.When more than four GPS satellites are visible,EDI is used to detect and isolate the abnormal GPS measurement data caused by multipath delays or interference.On the other hand,AKF is applied to update the covariance matrix of measurement noise by innovation covariance in real time to suppress the error introduced by GPS signal partly denial or road conditions such as turning or slope.Without adding sensors to the navigation system,the RKF model is proposed,and the TC MEMS-INS/GPS integrated navigation system integrated with the RKF is described.The effectiveness of the RKF is analysed.

This paper is organized as follows.Section 1 gives the TC INS/GPS integrated navigation principle briefly,and the integrated navigation solution errors introduced by GPS measurement data and measurement noise of the KF are analysed in theory.The model of the proposed RKF model is described in detail in Section 2,and the EDI and AKF integrated in RKF are presented as well.Finally,the improvement in the navigation solution of the TC MEMSINS/GPS integrated navigation system with the RKF model is tested and analysed by a vehicle-mounted experiment on an urban road.

1 Tightly coupled INS/GPS navigation system

1.1 Principle of TC integrated navigation

The TC INS/GPS integrated navigation system is realized in the range domain.The measurement input of the Kalman filter is the pseudorange and pseudorange rate from the GPS ranging processor,and the INS error,clock deviation and drift of the GPS receiver are estimated according to the measurement value.The output of the navigation system is the corrected inertial navigation parameter,which does not pass through the GPS navigation filter.The measurements of the pseudorange and pseudorange rate complement each other.Pseudorange derives from code tracking and is used to determine absolute position,while pseudorange rate derives from the carrier ring and is used to determine changes in position.

1.2 Kalman filtering model

1.2.1 State equation

Thekepoch state equation in KF for TC INS/GPS integrated navigation system is given as Eq.(1).

whereXkis the state vector ofkepoch;Fk,k-1is the state transfer matrix,including the error model of position,velocity,attitude,inertial sensor,receiver clock deviation and clock drift;Gk-1is the noise distribution matrix;andWk-1is white noise.

The state vector includes position error,velocity error,attitude error,gyroscope drift,accelerometer error,satellite receiver clock deviation and clock drift in the navigation coordinate system,as shown in Eq.(2).

1.2.2 Observation equation

The Kalman filtering measurement model in the discrete time domain is expressed as

whereZkis the measurement vector;Xkis the state vector;Hkis the measurement matrix;andVkis the measurement noise with covarianceRk.

In the TC INS/GPS integrated navigation system,the available measurements ofkepoch are pseudorange(ρk,INSandρk,GNSS) and pseudorange rateTherefore,as shown in Eq.(4),the measurement vector is the difference between the predicted value of INS and the measurement value of GPS.

1.2.3 Measurement noise and filtering gain

After the state estimate has been predicted by the Kalman filter,it needs to be corrected by the measurement.First,the minimum estimation of the root mean square error (RMSE) is achieved by calculating the Kalman filtering gain arrayKkbased on the measurement covarianceRk.The calculation of the gain array is given in Eq.(5).

As seen from the equation,Kkdepends on prior covariancePk/k1-and measurement noise covarianceRk.When a new measurement valueZkis obtained at thekepoch,it is compared with the predicted measurement valuebased on the prior state estimation,and then the difference is weighted byKkto update the prediction of the state vector to generate the best estimate.Therefore,the state estimation at epochkis given as Eq.(6).

According to Eq.(5) and Eq.(6),when the value ofKkis large,the measurement value will be given more weight;whenKkis small,the weight on the forecast is greater.In the TC INS/GPS integrated navigation system,when the GPS pseudorange and pseudorange rate measurement accuracies are high,the value ofKkis large,and the measurement covariance matrixRkbecomes relatively small.Otherwise,the value ofKkis small,and the measurement covariance matrixRkbecomes relatively large.In a practical environment,due to the change in the surrounding environment and navigation signal block,unforeseen GPS measurement error will be introduced into the navigation system,so the statistical feature of measurement noise is variable with observational error.However,the Kalman filter of conventional TC integrated navigation does not carry on EDI,and the stability of the filter and the precision of the navigation solution may be reduced due to the fixed measurement noise.Overall,it is necessary to detect and isolate the measurement errors and adjust the measurement noise according to the GPS observation conditions for filtering gain correction and adjust the weights of actual and predicted observations in the navigation system accordingly for a robust system.

2 Robust Kalman filter model

2.1 RKF model for TC MEMS-INS/GPS integrated navigation system

Fig.1 shows the RKF model proposed for the TC MEMS-INS/GPS integrated navigation system.The deviations of the pseudorange and pseudorange rate measurements from the GNSS receiver and the value predicted by the MEMS-INS are set as the measurement input of RFK.The navigation solution of position,velocity and attitude from the MEMS-INS are corrected by the output from RFK,and then the integrated navigation solution is obtained.RKF is constructed by the combined EDI and AKF procedure.In urban environments,the EDI is applied to eliminate outliers caused by GPS signal multipaths and interference when the number of visible GPS satellites (SVs) is more than four,while AKF is introduced to suppress the filtering divergence and generate the optimal integrated navigation solution.It should be noted that GPS observation EDI and AKF can be integrated into the TC INS/GPS integrated navigation system independently or simultaneously.The algorithm of EDI and AKF will be described as follows.

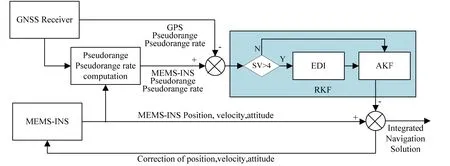
Fig.1 RKF model for TC MEMS-INS/GPS integrated navigation system

2.2 Error detection and isolation (EDI) procedure for GPS redundancy measurement

The EDI is based on the principle of innovation2χfault detection and is carried out when the number of visible GPS satellites is more than four.This section describes the2χfault detection and designs the EDI procedure.

2.2.1 Principle of innovation2χ fault detection

For the Kalman filter,the innovation vector of thekepoch is

In Eq.(8),Rkis the initial setting of measurement noise,Hkis the measurement matrix,andis the covariance matrix.

When a system fault occurs,the mean of the innovation vectorrkis no longer zero.Therefore,the mean value test of the innovation vectorrkcan also determine whether the fault occurs.The binary assumption is made for the innovation vectorrk:H0is no faulty,is faulty,.

The constructed fault detection function is given in Eq.(9).

whereλkis the2χdistribution obeying the freedom degreem,namely,λk～χ2（m）,which has been proved in reference.The amount ofmis twice the number of visible satellites.In this paper,we set the detection error ratePfas 10-6in EDI.According to the visible number,the preset thresholdTDis calculated as Eq.(10) in each measurement epoch in real time.Ifλk＞TD,the fault will be determined.

The innovation includes system model information and observation information,so the preset threshold can be used as the indicator of whether the state estimation is consistent with the observation value.For low dynamic vehicle-mounted INS/GPS integrated navigation systems,the navigation error caused by the system model is often much smaller than the observation error.Moreover,the system model error is controlled within a small range due to feedback correction in the closed-loop Kalman filter.Therefore,to a large extent,the innovation statistics reflect the anomalies of observations.

2.2.2 EDI

In general,the measurement value,including pseudorange and pseudorange rate of all visible satellites,will be given up due to the system error detected by the INS/GPS integrated navigation system,which will cause the waste of other measurement resources and the accumulation of measurement errors.To make full use of the observation epoch with fault,the detection and isolation method of observation fault process based on the principle of2χdetection of innovation is designed as follows:In the case that observation satellites have redundancy (the number of visible satellites is more than four),the fault detection function given in Eq.(9) is used to construct the fault detection function,and then the thresholdTDis calculated according to Eq.(10).Ifλk≤TD,no fault will be determined.In contrast,the calculated valueCkand theoretical valueAkof the innovation covariance matrix inkepoch can be obtained by Eq.(11) and Eq.(8).

By Eq.(12) to acquire the corresponding element difference of calculation values and theoretical value of innovation covariance matrix,then the observation error would be located from theiline position of maximum difference,so that the corresponding pseudorange and pseudorange rate measurement input are isolated from the measurement model of Kalman filter.In Eq.(12),Ck（i,i）andAk（i,i）are theirow andiline elements of diagonal matricesCkandAk,respectively;nis the size ofCkandAk.The adjusted satellite measurement information participates in the followed filtering calculation.

2.3 Adaptive Kalman filtering (AKF) algorithm

In the KF of TC integrated navigation,the measurement noise is a constant,but in urban environments,the navigation system will be affected by factors such as GPS signal observation conditions and carrier motion state changes,resulting in the corresponding change in measurement noise characteristics.Therefore,it is necessary to adjust the measurement noise adaptive according to the changes in the measurement data to improve the robustness of the filter.

In this section,an AFK algorithm based on innovation is presented.The adaptive filtering factor is constructed by the statistical average value of the innovation variance measurement and the theoretical value in the sliding window to adjust the initial setting measurement noise and further enhance the robustness of filtering.In the same Kalman filtering period,the occlusion or interference conditions of all observation satellites are different,so the adaptive factor will adjust the pseudorange and pseudorange rate measurement noise of each GPS satellite.

In the interval of sliding window lengthN,the statistical variance of measurement innovation of thekepoch is,which is used to represent the statistical characteristics of measurement innovation variance in the current period,and its expression is given in Eq.(13).

The statistical variance of theoretical innovation of thekepoch is,which is used to represent the statistical characteristics of theoretical innovation variance in the sliding window period,and its expression is given in Eq.(14).

The length of the calculated sliding window is set according to the changes in the surrounding environment of the vehicle.The window size can reflect the sensitivity of the constructed filter.The shorter the window is,the higher the sensitivity,which may lead to the insufficient characterization of the statistical characteristics of measurement noise.Otherwise,they lose the ability to track short-term changes.We set length of the sliding window as 5 in this paper.

iis set as the serial number of the observation satellite of thekepoch,Mis the number of satellites that can be used as measurement input after fault detection and isolation,andγkis the adaptive factor vector of thekepoch.The calculation method is given in Eq.(15).

TρandTρ˙are the detection thresholds for the pseudorange and pseudorange rate difference of the corresponding diagonal elements in the measurement and theoretical innovation matrices,and they are set as 5 and 4.5 in this paper.After adjusting the adaptive factor,the measurement noise of thekepoch is,and its expression is in Eq.(16).

3 Field test and analysis

To test the performance of RFK given in Section 2,vehicle-mounted experiments are carried out in the urban area of Xi'an,China,where GPS signals may be blocked by buildings and street trees,leading to fewer than four observation satellites,and disturbances may be introduced by wireless signal refraction.In addition,vehicle experiences large changes in their movement state due to turning or slope on urban roads.In this section,the experimental design and results analysis are presented.

3.1 Experimental design and device

3.1.1 Experimental platform

As shown in Fig.2,the field experimental platform includes two GNSS receivers,one inertial navigation device and one data processing computer.The specifications of the inertial navigation device are shown in Tab.1.Among them,one GNSS satellite receiver is NovAtel 718D,and the other is Trimble BD930.The INS is the Micro-Electro-Mechanical System (Micro-Electro-Mechanical System,MEMS) inertial navigation system Ekinox 2 produced by SBG Company,and the INS/GPS integrated navigation solution with high precision can be output by accessing the measurement data of the satellite receiver.The computer is used to achieve the experimental data acquisition and processing of RKF.

Fig.2 Field experimental platform

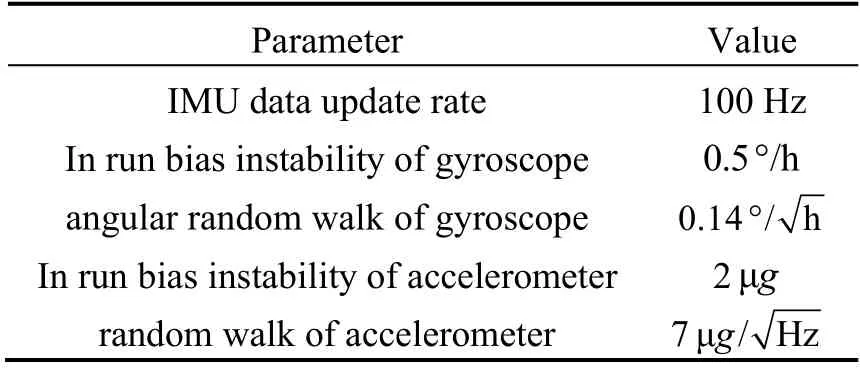
Tab.1 Specifications of INS

The connection relation of all experimental equipment is shown in Fig.3.GPS signals received by the antenna are transmitted to the Trimble BD930 receiver and NovAtel 718D receiver through the power distribution amplifier.The NovAtel 718D receiver simultaneously receives the RTK data to achieve differential positioning and inputs the measurement data to the SBG Ekinox inertial device.Trimble BD930 transmits the measured pseudorange and pseudorange rate data to the computer;SBG Ekinox inertial navigation transmits the measurement of the specific force and angular rate to the computer,receives the measurement data of the navigation receiver,and outputs the integrated navigation solution locally as the reference of the navigation solution due to its highest accuracy.The computer receives the measured values of the Trimble BD930 receiver and SBG Ekinox inertial navigation,GPS measurement is selected for integrated navigation system.We use the KF,EDI,AKF and RFK model to process the data respectively,and then analyses the experimental results.

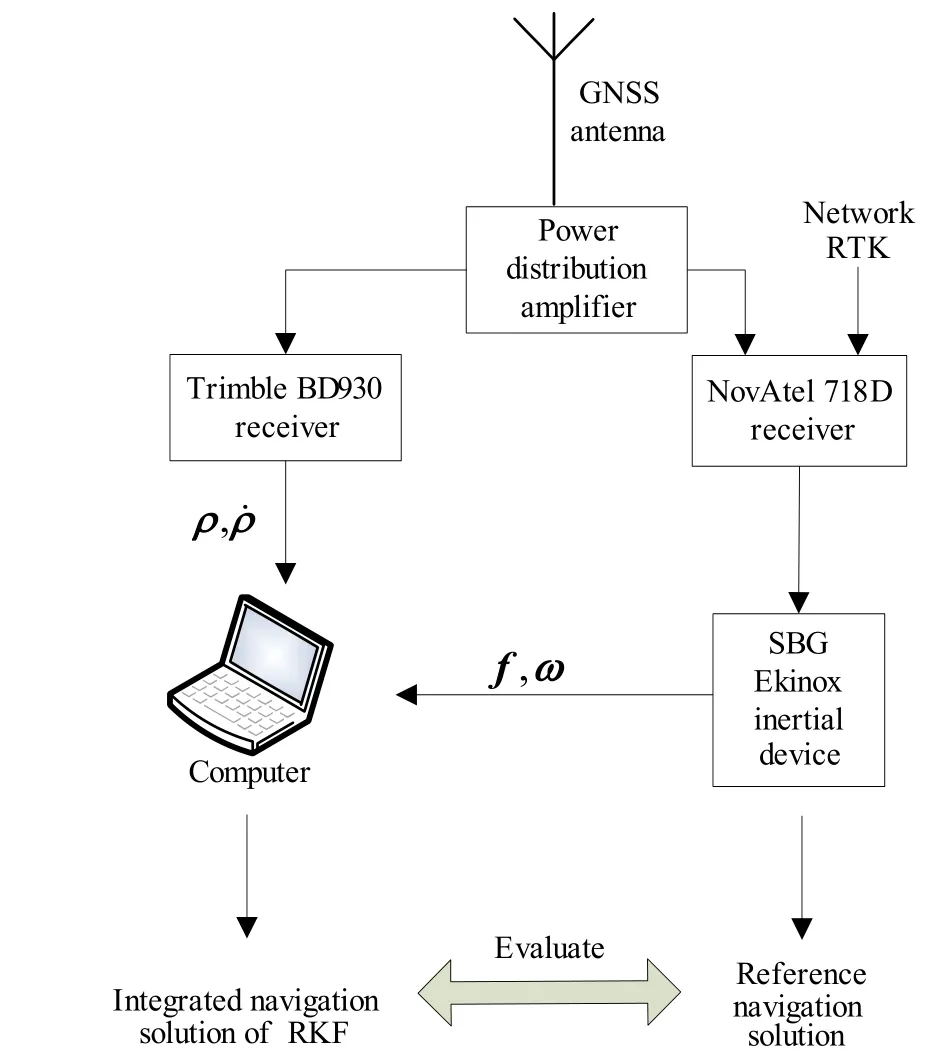
Fig.3 Connection relation and data flow diagram of the experimental device

3.1.2 Experimental design

The navigation solutions of KF,AKF and RKF are compared with the integrated navigation solution from SBG Ekinox,which is used as a reference to evaluate the effectiveness of the RFK model proposed in this paper.Fig.4 shows the reference trajectory,and the journey is nearly 10 km.GPS signal may be challenged by the urban environment.

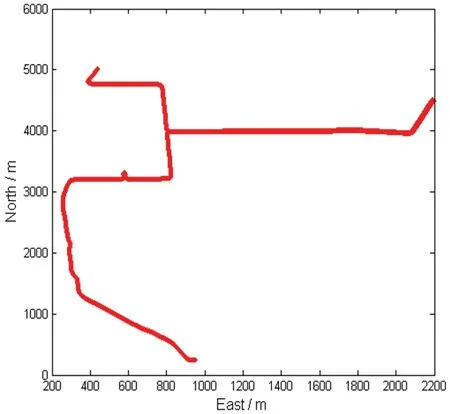
Fig.4 Reference trajectory

The total duration of the experime nt was 1200s,and the number of GPS visual satellites less than four was 45s,accounting for 3.75%,during which the navigation solution could not be obtained through the GPS.As is presented in Fig.5,the duration of PDOP (Position Dilution of Precision) value greater than 4 was 366 s,accounting for 30.5%.At some point,the PDOP value even exceeds 10.So we can draw a conclusion that GPS measurement with large errors may be entered into observation equation of Kalman filter during the journey.

Fig.5 PDOP

3.2 Experimental results and analysis

3.2.1 Analysis of general experimental results

According to the reference trajectory given in Section 3.1.2,the KF of TC integrated navigation,the EDI given in Section 2.2,the AKF presented in Section 2.3 and the RFK combined EDI with AKF algorithms are used to process whole measurement data and obtain the navigation solution of horizontal positioning,height and velocity.Using the navigation solution from SBG Ekinox as a reference,RMSEs are calculated to evaluate the performance.

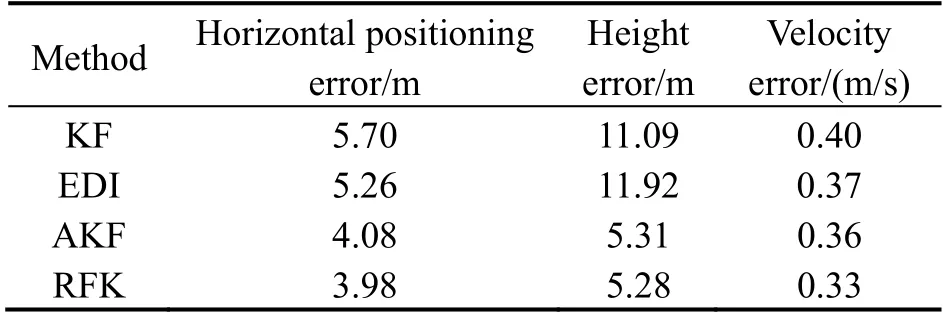
The experimental results are shown in Tab.2.Compared with the conventional KF of TC INS/GPS integrated navigation system,the accuracy of the navigation solution is improved whether the EDI algorithm or AFK algorithm is added to the TC integrated navigation system alone or both.However,the accuracy of the height solution was slightly impaired after the EDI is added alone to KF due to the loss of satellite resources.At the same time,it can be seen that AKF has a more obvious effect than EDI on navigation solution error suppression.The RFK model combined with the EDI and AKF algorithms has the most obvious suppression effect on position and velocity errors,especially for height errors.The position errors in the horizontal direction decrease from 5.70 m to 3.98 m,which is a reduction of 30.18%.The height error decreased from 11.09 m to 5.28 m,a reduction of 52.39%.The velocity errors decreased from 0.40 m/s to 0.33 m/s,which is a decrease of 17.50%.

Tab.2 RMSE of positioning and velocity

3.2.2 Performance analysis during GPS signal partly denial

During the experiment,the number of visible satellites will change correspondingly when the GPS signal is blocked by street trees or urban buildings,as shown in Fig.6.In the region where GPS signals are severely blocked (approximately 500 s,590 s and 800 s),the number of visible satellites is less than four and more than two,and the duration varies from 10 s to 30 s.At this time,navigation solutions by GPS satellite positioning cannot be conducted,and the horizontal position solution will produce large errors.At the positions of 500 s and 590 s,the horizontal position error of KF increases and exceeds 10 m.Meanwhile,it is obvious that the maximum error has exceeded 30 m at 800 s.RFK and AKF can effectively suppress the horizontal positioning errors caused by an insufficient number of visible satellites.At 500 s and 590 s,the maximum horizontal positioning errors are reduced to less than 5 m.At 800 s,the maximum error is less than 10 m.Besides,the EDI in RFK model restrains outliers of horizon positions at approximately 820 s.

Fig.6 Number of visible GPS satellites and errors of position

Due to GPS signal outrage,the velocity errors also increase correspondingly,as shown in Fig.7.The RFK model decreases the maximum velocity residual error at intervals of 500 s and 800 s.Furthermore,the EDI in RFK also eliminates the outliers of east and north velocities at approximately 820 s.

Fig.7 Number of visible GPS satellites and velocity errors

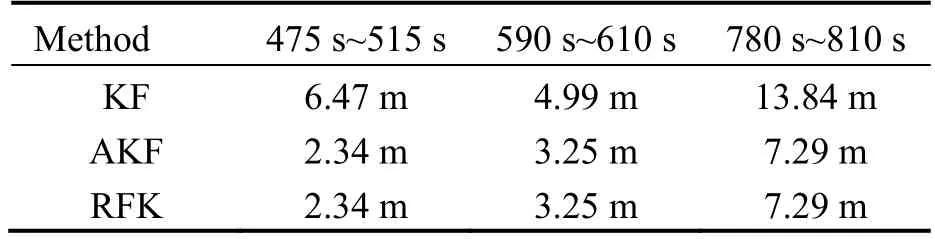
In Tab.3,the horizontal position errors of three periods are analysed when the visible satellite number is less than four.The RMSE of the KF,AKF and RFK algorithms within this period is calculated,and the improvement in the horizontal position error during GPS signal short outrage is presented.Compared with KF,the error of RFK decreases in these three intervals are 63.83%,34.87% and 47.33%,respectively.Due to the pause of the EDI when the number of visible satellites is less than four,the AKF and RFK have nearly the same accuracy.

Tab.3 RMSE of horizontal position during GPS signal partly denial

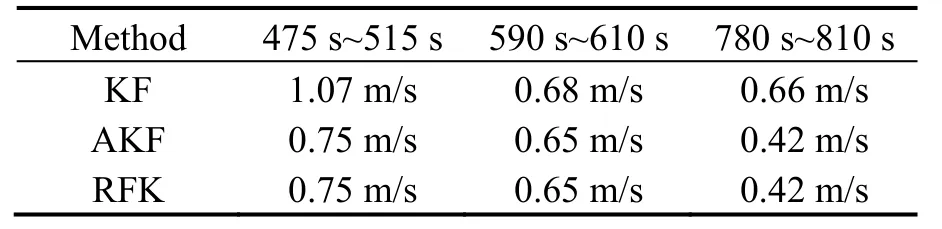
The height position errors of three periods of GPS signal short outrage are presented in Tab.4 when the visible satellite number is less than four.Compared with KF,the error of RFK decreases in these three periods are 36.80%,68.01% and 81.33%,respectively.So RFK has more obvious effect on height position error suppression than horizon position.The AKF and RFK have nearly the same accuracy due to the pause of EDI in RKF.The velocity errors in these three test periods are analysed in Tab.5,and the RMSE of the velocity solutions obtained by KF and RFK in the three periods are calculated.Compared with KF,the velocity errors of RFK are obviously reduced,and the decrease rates were 29.91%,4.41% and 36.36%.AKF and RFK also have nearly the same accuracy on velocity due to the same reason for position measurement.

Tab.4 RMSE of height position during GPS signal partly denial

Tab.5 RMSE of velocity during GPS signal denial partly

3.2.3 Performance of RFK in Urban Traffic Situation

The straight,turning and slope trajectories are the most common traffic situations in urban areas.The horizontal position precision for straight and turn running as well as the height trajectories are analysed in this section using KF,AKF and RFK for data processing correspondingly,and the navigation solution from SBG Ekinox is used as the reference (REF) for evaluation.The trajectories of straight and turn running are shown in Fig.8.Compared with the KF method,the AKF and RFK improve the horizontal positioning accuracy of both straight and turning running,and the improvement is more obvious in the turning section.The AKF and RKF share almost the same accuracy.

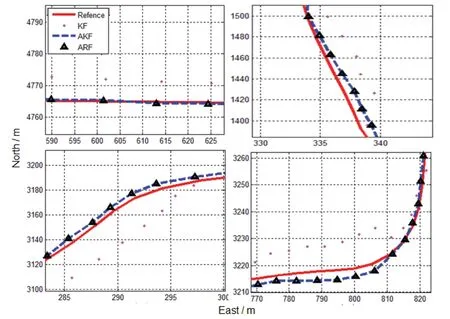
Fig.8 Comparison of straight and turning trajectories

To evaluate the accuracy of the height position,we compare the height tracks processed by KF,AKF,and RKF with the reference height position in Fig.9.Similar to the evaluation result of horizontal position accuracy,the AKF and RKF share nearly the same performance on height position measurement,and they both have great improvement on height measurement compared with KF,especially for the period with great change on height(650 s～1000 s),so RKF has the advantage of height measurement for the slope of urban traffic.

Fig.9 Comparison figure of height trajectories

4 Conclusion

A RFK model is proposed for the TC INS/GPS integrated navigation system in this paper.After GPS observation errors by EDI,an adaptive filtering factor is constructed by the innovation covariance,and then the measurement noise covariance is adjusted to enhance the robustness of the TC integrated navigation system.

The field experiment results show that compared with KF for TC INS/GPS integrated navigation,the errors of navigation solutions are reduced whether the EDI algorithm or AFK algorithm is added to the navigation system alone or both,and the RFK mode combined both algorithms has the most improvement.It can effectively reduce the velocity error and the position error in the horizontal direction and height direction by 17.5%,30.18%and 52.39%,respectively,and the position error in the height direction is the most effective.In addition,for the three test periods when the GPS signal is partially denied and the number of observable satellites is less than four,the RFK reduces the horizontal and height position error significantly compared with the KF.The horizon position error of one period decreases approximately 30% and the other two periods by 63.83% and 47.4%,while the errors reduction on height position are more obvious,they are 36.20%,67.75% and 81.99%,respectively.In terms of velocity error,the velocity error of one period decreased by nearly 5%,and the other two periods decreased by approximately 30%.Furthermore,RFK can effectively reduce the positioning error of TC integrated navigation systems on horizon and height direction,and the effect is more obvious in traffic situations such as turning and slope in urban areas.

The RFK model presented in this paper can effectively suppress navigation solution errors such as position and velocity in urban environments and effectively improve the robustness of TC INS/GPS integrated navigation systems.