USBL安装偏差联合模型构建与校准方法

刘慧敏，陆 凯，单 瑞,2，杨 源，李勇勇，杜 凯

（1.中国地质调查局青岛海洋地质研究所，青岛 266237；2.自然资源部海底科学重点实验室，杭州 310012；3.天津航海仪器研究所，天津 300131）

超短基线声学定位系统（Ultra Short Baseline System,USBL）广泛应用于水下科学考察、离岸海底勘探、海洋工程以及水下导航等领域。作为全球卫星导航系统（Global Navigation Satellite System,GNSS）、航姿参考系统（Attitude and Heading Reference System,AHRS）、声学测距与测向技术的结合，USBL 的安装偏差校准是维持不同测量系统坐标参考框架统一的关键[1-3]。USBL 的角度安装偏差是指USBL 换能器的仪器坐标系与船体坐标系之间的角度偏差，固定安装后一般保持不变，而随着测量距离的增加，角度安装偏差成为影响USBL 深海远距离定位精度的重要因素。因此USBL 在安装使用前，必须要进行严格的角度安装偏差校准。校准时一般利用提前布设的水下校准信标，将安装偏差校准等效于参数估计，可对换能器水平距离安装偏差和角度安装偏差进行最优估计。然而，受国外研发机构和商业公司对USBL 校准技术的商业保护，USBL安装偏差校准的数学模型、方程和数值算法研究均鲜有公开。

国际上，法国海洋开发研究所的Opderbecke[4]首次构造了含有角度安装偏差旋转矩阵的目标函数，并采用循环迭代的方式计算角度安装偏差。该方案执行相对简单，但无法估计安装位移偏差和声速误差的影响。中国台湾的chen 等[5]基于规则的几何航迹下角度安装偏差对定位误差的不同影响进行几何求解，但测量船要按严格的轨迹航行才能得到理想的校准效果。2005年，唐秋华和吴永亭等[6]人首次提出将参数估计方程拆为两步，第一步是根据距离交汇估计目标应答器或者安装位移偏差；第二步是采用一定的准则根据定位方程估计角度安装偏差。两步法校准方案提出后，国内武汉大学、海洋二所和哈尔滨工程大学都基本采用了该校准方程，并深入研究了该校准方法，取得了一系列有意义的研究成果[7-10]。2019年，孙大军等[11]提出利用矩阵分解对三个姿态角度偏差进行解耦，提高了校准精度，但需要已知参考信标的坐标。近年来，还有学者结合船载惯性导航系统或多普勒计程仪，通过构造含超短基线的角度安装偏差的误差方程，滤波解算USBL 的安装失准角，获得了较高的精度[12-15]。这类方法属于USBL 和组合导航设备直接的角度偏差校准，不属于本文研究范畴。

基于以上的研究成果，本文进一步研究了校准的联合数学模型和数值算法，提出一种USBL安装偏差校准方案。不同于以往将参数估计方程进行拆分的校准方案，本文首先结合克罗尼克积给出高斯-马尔科夫数学模型假设下的参数估计联合解，然后基于失准矩阵初始解和协方差矩阵求解其固定解。同时联合模型还可以对距离安装偏差、声速误差进行增广，提高模型的适用性。结合南海的USBL 校准试验验证了所提方案的性能。

1 USBL 校准原理与联合模型

如图1所示，校准前首先需要布设海底超短基线校准信标。校准过程中，安装有超短基线换能器的测量船沿着校准轨迹航行，同步采集并记录GNSS 定位数据、船的航向和姿态数据以及声学相对定位数据（测距和测向信息）。数据采集模式一般分为静态模式（定点）采集数据和动态模式（走航）。静态模式时校准位置位于信标的正上方的四个方位和等水深固定方位的四个校准点进行采集，每组采集的数据个数相同。动态模式基于船的直线航向，航迹规划一般可分为四方位和八方位的直线校准模式，通过对称的航迹采集数据[18]。

图1 联合海底信标的USBL 校准示意图Fig.1 USBL calibration schematic with the seafloor beacon

设k时刻GNSS 天线在导航坐标系下的位置为，USBL 校准信标在导航坐标系下的坐标为，GNSS 和USBL之间的固定安装距离偏差为为换能器相对于海底校准信标的声学相对位置，其数学关系如下：

传统的两步法计算方案首先对式(1)变形并求模，得到其距离观测方程：

不同于以往的两步法校准模型，本文直接将式(1)进行变形，并构造新的数学模型。首先，通过对式(1)移项并左乘，可得：

式(4)的左侧可视为已知的3×1 观测值矩阵，其右侧可视为系数矩阵和位置参数组合。设USBL 采集了m对校准数据，根据式(4)构造高斯-马尔科夫模型：

其中，Y为3×m的观测值阵，；A为 3m×3 的系数阵，；PU为m×3 的矩阵，且；QY为3m×3m的协方差矩阵；⊗表示克罗尼克积运算，且满足运算：表示求矩阵的拉伸向量，可将矩阵内的元素按列自左到右依次首尾相接，重组成只有一列的向量；E()·表示数学期望；D()·表示数学方差。

构造以上的高斯-马尔科夫模型并结合矩阵克罗尼克积与拉伸向量运算，便于直接求姿态旋转矩阵的初始解和条件协因数矩阵。将式(5)的高斯马尔科夫模型构造成代价函数参数估计问题：

2 联合校准模型的数值算法

2.1 联合模型的初始解

其条件协因数矩阵为：

初始解虽未考虑姿态旋转矩阵的正交性，但给出了姿态旋转矩阵在随机框架下的最小二乘最优解和条件协因数矩阵。

2.2 联合模型的固定解

若考虑姿态旋转矩阵的正交性，可以通过求解随机框架下的最小二乘最优解和条件协因数阵，即等价于求式(12)代价函数参数估计问题：

其中，λ为已知的阻尼矩阵。在迭代过程中利用残差向量与改正数构造迭代判断条件，通过选择合适的阻尼尺度因子与阻尼矩阵相乘或相除，使得阻尼矩阵可在迭代过程中自适应调整。

图2 为简化的迭代流程。

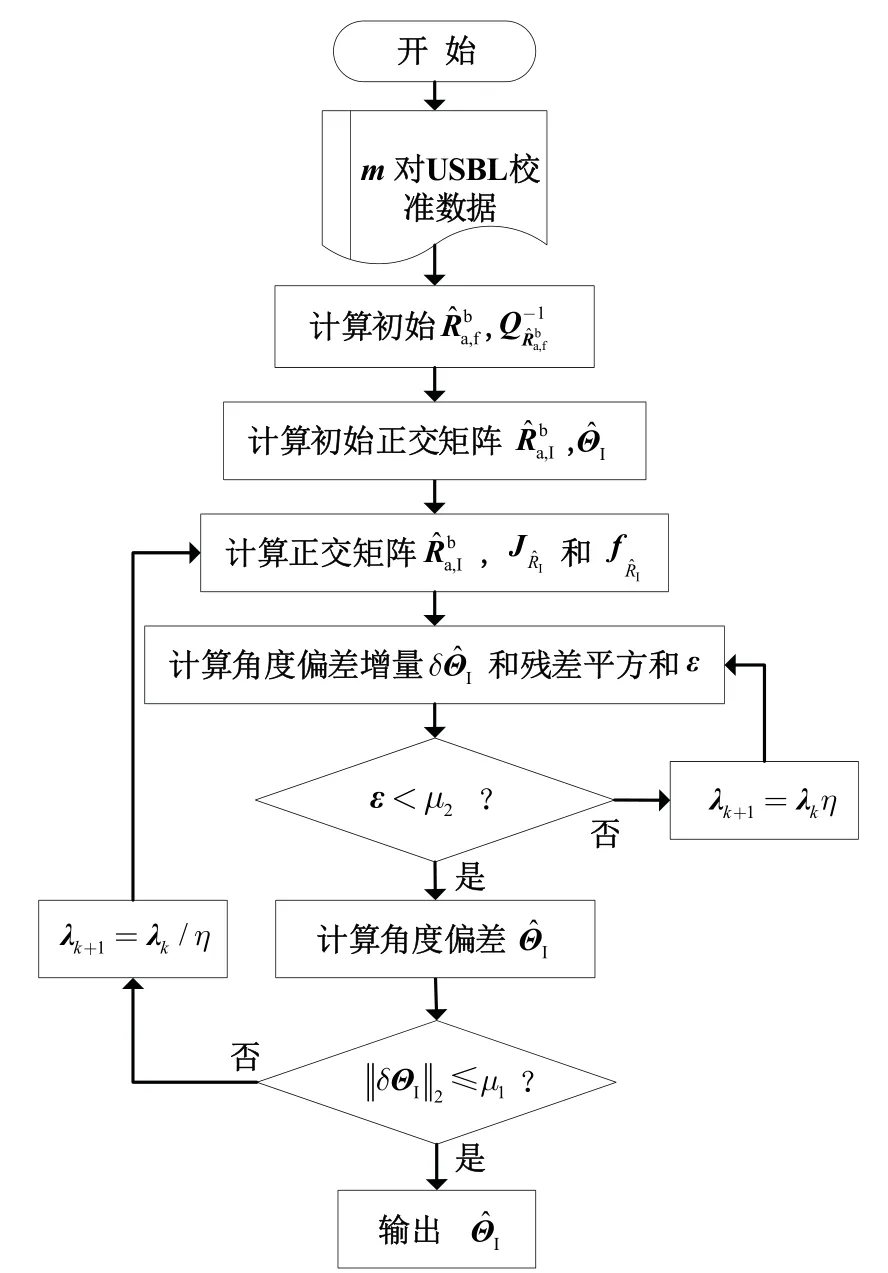
图2 基于LM 迭代法的角度安装偏差解算流程图Fig.2 Flow chart of angle installation deviation solving based on LM iterative method

（1）选择迭代终止参数μ1和μ2，可由经验或设备测距精度选择合理的较小值。阻尼矩阵λ初始值可选择为单位阵，阻尼尺度因子η通常为较小值。根据输入的，通过式(13)(14)计算。

（4）进行迭代判断：

如果ε＜μ2，则。如果，此时停止迭代，输出最优解。如果，则，并重新从步骤（2）继续计算。

如果ε≥μ2，则，并重新从步骤（3）继续计算。

（5）输出角度安装偏差的最优解。

得到角度安装偏差的最优解时，还可以基于角度安装偏差的最优解，计算校准信标更准确的坐标和其条件协方差矩阵。

3 联合校准模型的增广

3.1 换能器水平距离安装误差补偿模型

若考虑式(1)中换能器水平距离安装误差的校准，对式(1)增广为：

其中，B为3m×2 的系数阵，。将式(19)转化为构造代价函数的参数估计问题：

基于克罗尼克积的法方程表示为：

3.2 声速误差补偿模型

若校准过程中无法获得准确的声速剖面，由于USBL 校准航迹的入射角聚类清晰，本文给出一种简化的声线弯曲补偿增广模型[18]：

对式(22)变形并求模，其测距观测方程表示为：

4 实验验证

为验证本文提出的联合校准数值算法的精度，在南海海域进行了USBL 的校准试验，如图3所示。安装浮力衣的USBL 校准释放信标布放深度约为115 m，由测量船搭载的康斯伯格HiPap 102PMGC 超短基线定位系统进行了静态模式校准数据采集。定位系统采用Veripos APEX 差分GNSS 接收机，水平定位精度优于0.1 m。采用HiPap 102P MGC 集成的姿态测量模块提供姿态数据，并同步采集校准信标的相对位置。试验区的平均声速为1489.7 m/s。具体参与校准的导航设备性能参数如表1所示。

图3 USBL 校准试验概图Fig.3 The sketch of USBL calibration test

表1 设备参数Tab.1 Equipment parameter

图4 为静态模式下测量船依次在校准信标四个等距离（一般使用等水深）点采集的四组静态数据，距离信标的平面距离约100 m，然后在校准信标正上方的四个方向（90 °夹角）各采集四组静态数据，共八组。每个采样点取200 个声学定位数据，并结合GNSS和姿态数据构成校准数据对，共1600 对。

图4 USBL 静态校准的GNSS 采集位置Fig.4 Position of GNSS with USBL static calibration

图5 给出了校准过程中的航向角历元序列，表2给出八组数据的航向以及换能器与应答器之间水平距离的均值和方差统计量。静态模式开启动力定位后，航向角均方差保持在1 °以内，除第四和第六组数据外，其余的测距均方差优于1 m，测量船换能器的航向角和海面位置符合校准要求。

图5 USBL 静态校准的航向Fig.5 The heading of USBL static calibration

表2 测量船八组观测的空间位置统计Tab.2 Statistics of spatial position observed by eight groups of survey ship

如图6所示，依靠动力定位，纵摇角最小值和最大值分别为-2.3 °和2.1 °，平均值为-0.47 °；横摇角最小和最大值分别为-2.7 °和2.8 °，平均值为0.01 °。整个校准期间的航向数据和姿态数据维持稳定的状态，基本满足动力定位要求的3 m 以内的定位精度以及四级海况下横纵摇2.5 °左右，保证了校准期间的定位和姿态精度。

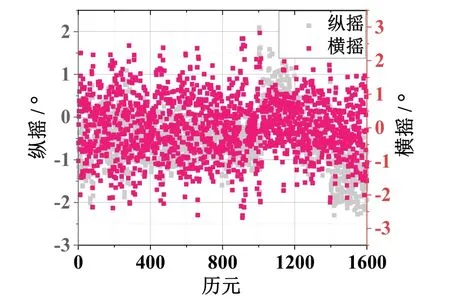
图6 USBL 静态校准的姿态数据Fig.6 The attitude of USBL static calibration

整个校准期间应答器的信噪比（信号/噪声）如图7所示，其中信噪比值越高，说明环境噪声越低。信噪比跟测量船与信标的相对位置有关。校准期间测量船在校四个等距离点时所采集的四组静态数据信噪比最高，而在信标的上方时，信噪比相对较低。

图7 USBL 应答器信噪比Fig.7 USBL transponder signal-to-noise ratio

USBL 未校准时，由于存在未校准的角度安装偏差（约5 °）和距离安装偏差，此时水下信标的平面位置较为分散，且存在一定聚集特征，如图8所示，图中DRMS 表示1600 组数据求出的平面定位均方根误差。

图8 USBL 未校准时的水下信标平面位置Fig.8 The horizontal position of underwater USBL beacon without calibration

为验证本文的联合校准数值算法的精度和有效性，同时采用了传统的两步法校准算法、联合校准数值算法和康斯伯格配套的后处理软件APOS 校准模块最终解算报告进行对比分析，其中，APOS 后处理软件解算的距离安装偏差和角度安装偏差与联合校准法基本一致，图9 给出两步法和联合法的平面定位散点图。

图9 两种方法解算的信标平面位置Fig.9 The horizontal position of USBL with two methods

传统的两步法校准算法和联合校准数值算法解算的信标位置残差在北向、东向和垂直方向统计如图10-12所示。可知无论是两步法还是联合法都可以求得信标的坐标、距离安装偏差和角度偏差，基本满足USBL 的校准需求。与两步法相比，联合法的北向、东向和垂直方向的定位残差高斯分布概率密度曲线的对称轴更接近0，更为细长且对称分布。原因在于，处理过程中对参数进行联合解，顾及了USBL 的方向信息对海底信标位置和距离安装偏差的影响，从而三个方向的定位残差更接近0，具有更好的聚敛性，进而提高了校准的精度。

图10 两种方法解算的北向定位残差统计图Fig.10 The position residual bar in northing with two methods

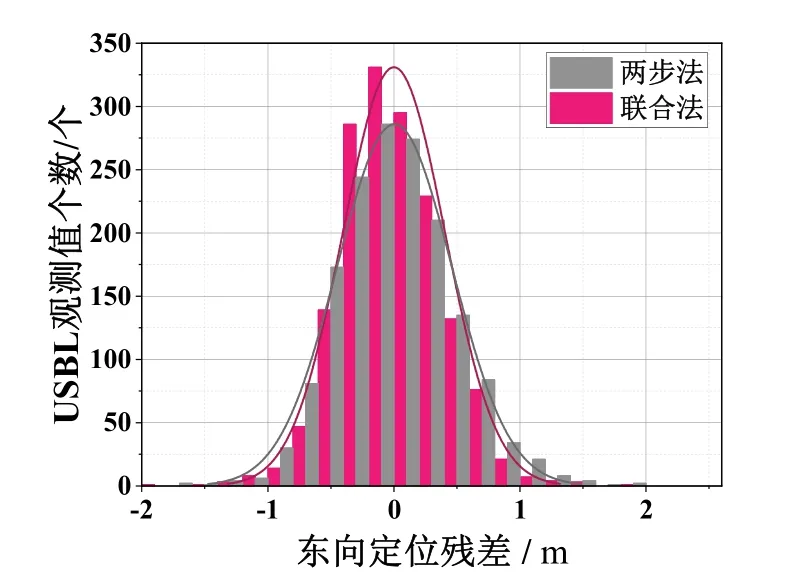
图11 两种方法解算的东向定位残差统计图Fig.11 The position residual bar in easting with two methods

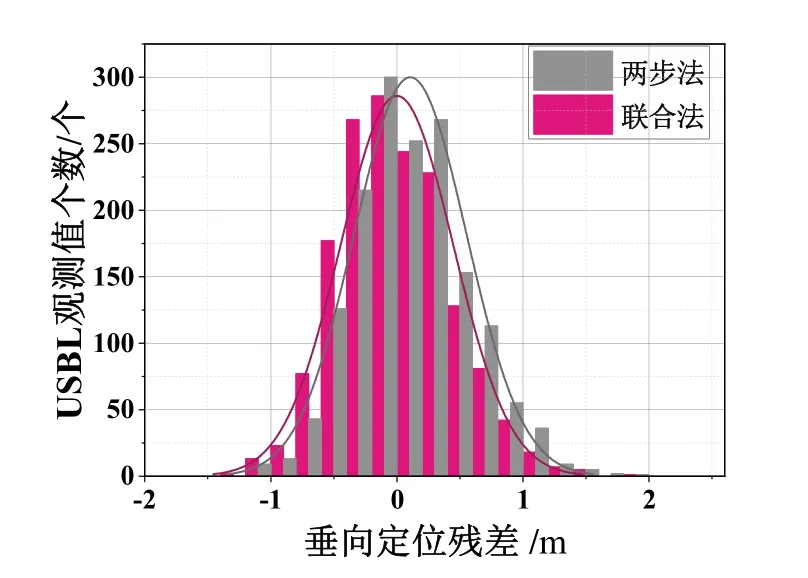
图12 两种方法解算的垂直方向定位残差统计图Fig.12 The position residual bar in vertical with two methods

进一步比较联合方法的精度，对信标定位误差、距离安装偏差和角度安装偏差进行了统计，如表3所示。同时采用康斯伯格公司配套的后处理软件APOS对距离安装偏差和角度安装偏差进行了同步的标定。对比三种方案的结果，两步法水平定位偏差的RMS约为0.69 m，联合法的RMS 约为0.60 m，提高了0.09 m，本文方法求解的信标水平位置的RMS 提高了约13%，垂直定位精度与两步法相当。联合法解算的水平距离安装偏差RMS 为0.04 m，两步法RMS 为0.26 m。USBL 校准观测的平均斜距约为137 m，根据式(25)以及水平定位偏差的RMS计算角度安装偏差精度，两步法解算的精度为0.29°，而联合法约为0.25 °。联合法同APOS 软件结果相比，二者结果非常接近，分析可能造成不一致的原因在于本文需要验证两种算法的理论精度未舍去稍微超限的6 组数据。

表3 信标定位误差、距离安装偏差和角度安装偏差精度统计表Tab.3 Positioning error,distance installation deviation and angle installation deviation accuracy statistics

为了验证本文提出的增广模型的有效性，采用六种方案进行两组实验，并进行对比分析。方案1：未考虑换能器水平距离安装误差的联合法；方案2：考虑换能器水平距离安装误差的两步法；方案3：考虑换能器水平距离安装误差的联合法；方案4：未考虑声速误差的联合法；方案5：考虑声速误差的两步法；方案6：考虑声速误差的联合法。其中方案1、方案2和方案3 对换能器水平距离安装误差补偿模型进行测试；方案4、方案5 和方案6 对声速误差补偿模型进行测试。

实验一：设换能器水平距离安装偏差为[2 m,1 m]。

基于式(26)给出了方案1、方案2 和方案3 解算的测距相对误差。

对比三种解算方案，如图13所示。由于方案1未考虑换能器水平距离安装误差的影响，其解算的精度最差。特别在第二组和第三组采样时，由于GNSS接收机、换能器与校准信标的相对位置的关系，其测距误差受到的影响最大。而考虑到水平安装距离偏差，本文方法解算的测距相对误差明显优于传统的两步法，验证了本文方法对测距安装误差和角度安装偏差进行联合求解的有效性。

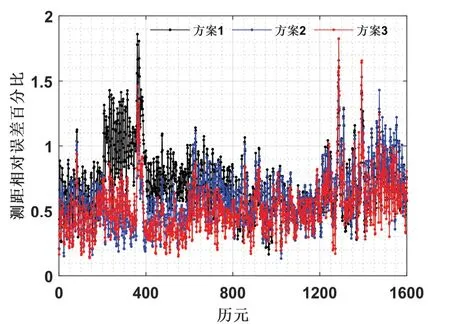
图13 方案1、方案2 和方案3 解算的测距相对误差Fig.13 Distance relative error for scheme 1,2 and 3

实验二：设声速误差为10 m/s。

对比三种解算方案，如图14所示。由于方案4未考虑声速误差的影响，其解算的测距精度最差。考虑声速误差，本文方法和两步法解算的测距相对误差基本一致，主要原因是本文方法和两步法同样对观测模型进行了求模运算，二者求解的声速误差一致。实验验证了本文方法对声速误差和角度安装偏差进行求解的有效性。

图14 方案4、方案5 和方案6 解算的测距相对误差Fig.14 Distance relative error for scheme 4,5 and 6

5 结论

本文提出了一种超短基线定位系统联合校准的数值算法。与以往仅用距离观测解算校准信标位置的两步法思路不同，本文方法充分利用了USBL 的方位观测信息，结合克罗尼克积给出高斯-马尔科夫数学模型假设下的校准信标位置和姿态失准角参数估计联合初始解，基于失准矩阵初始解和协方差矩阵利用Levenberg-Marquardt 迭代法计算三个姿态失准角。联合校准模型顾及了USBL 的方向信息对海底信标位置和距离安装偏差的影响，并对换能器水平距离安装偏差、声速误差等校准参数进行增广，可根据实际情况选择和解算USBL 校准参数。南海实测试验结果表明，相比传统的两步法，本文方法求解的信标水平定位偏差RMS 提高了0.09 m，水平距离安装偏差RMS 为0.04 m，角度安装偏差RMS 约为0.25 °，其距离和角度安装偏差与APOS 后处理软件结果基本一致，通过对参数进行联合解，提高了校准精度，具有工程应用价值。