基于旋转双棱镜的光束复合跟踪控制技术

王俊尧，宋延嵩，刘洋，张季丰

（长春理工大学 光电工程学院 光电测控与光信息传输技术教育部重点实验室， 长春 130022）

0 引言

近年来，光电跟踪技术快速发展，并在空间激光通信、激光武器等领域得到广泛应用［1-4］。传统光电跟踪系统多采用多轴伺服转台或光学反射镜来实现光轴调整，以确保对目标的准确跟踪。然而，它们通常具有较大的体积和质量，载荷的大转动惯量带来的动态滞后需要更高功率的伺服电机克服，并且对于振动的过度敏感性也对其动态跟踪性能产生了影响。为了解决上述问题，一些小尺寸大视场的新型光电跟踪系统受到广泛关注，如光学相控阵、旋转双棱镜、微型反射镜等［5-7］。其中，旋转双棱镜是小惯量光束伺服系统的典型代表，它由一对具有特定楔角的圆形光学棱镜构成，两个棱镜以相同的中心轴旋转实现光束的快速偏转，具有精度高、转动惯量小、光束指向快、振动敏感性低等优点［8-9］，这使得双棱镜系统在激光通信、干涉测量、光电探测等领域具有重要的实用价值［10-14］。

实现双棱镜目标跟踪的关键是揭示光束传递的非线性变化机制，并制定有效的棱镜控制策略。各国对于旋转双棱镜进行了大量研究，LAVIGNE V等［15］提出了一种基于旋转双棱镜的步进凝视成像系统，通过双棱镜的同轴旋转可实现连续的视轴偏转。LI A等［16］探讨双棱镜结构参数对于扫描盲区的形成规律，指出了光束扫描奇异性是限制光束扫描区域的重要因素。周远等［17］研究了光束指向与双棱镜角度的解析关系，并采用光线追迹方法来探讨其光束偏转机制。邱赛等［18］采用光线矢量传播方法建立了光束指向模型，并分析了旋转双棱镜系统误差对激光通信的指向精度的影响。WANG Z等［19］提出了一种基于旋转双棱镜的成像系统，用于实现超分辨率成像和视场扩展系统。LI A等［20］通过迭代求解方式得到了双棱镜系统的逆向公式，用于在给定光束指向的情况下获取双棱镜的旋转角，但缺少对于双棱镜跟踪系统的建模及瞄准控制策略，因此难以对移动目标进行成像跟踪。WANG J等［21］提出了一种针对超表面Risley天线的相位方法，给出了波束方向预测和偏转方向恢复的解析式，并将新方法与传统近轴近似方法进行了比较，揭示了两者之间的联系和区别。ZHOU Y等［22］研究了出射光束的回转率和两个棱镜所需的角速度，提供了有效的解析解，但还需要进一步分析目标运动和棱镜角速度之间的关系才能应用于动态目标的成像跟踪。LI A等［23］提出一种使用双棱镜的闭环视觉跟踪系统，并演示了径向-周向解耦控制策略，该方法虽然可以实现视线调整，可较长的视轴解算耗时令其难以获得良好的动态跟踪效果。ROY G与LI A 等［24-25］还探索了两组双棱镜的组合模式，通过扩大跟踪视野和粗精耦合方法进行目标跟踪。然而，两组棱镜级联令控制策略变得更加复杂，并牺牲了系统的实时跟踪性能，导致其不适用于动态成像跟踪领域。

以往对于旋转双棱镜的研究多集中在其模型求解与扫描成像问题上［26-27］，而在动态视轴控制和跟踪领域的研究较少。本文提出了一种基于旋转双棱镜的光束复合跟踪技术，通过建立双棱镜的光束传递模型，得到了动态跟踪时的棱镜旋转与光束偏折关系。在此基础上，提出采用快速反射镜（Fast Steering Mirror，FSM）修正双棱镜光轴偏差的复合跟踪系统，通过光轴解耦补偿和改进控制器以提高双棱镜的跟踪性能，最后搭建实验系统验证了基于旋转双棱镜的光束复合跟踪技术的可行性。

1 双棱镜系统的光束传递建模

1.1 双棱镜光束偏转模型

双棱镜光束传递的建模求解是实现光束跟踪的重要环节。基于近轴光学理论，将折射棱镜等效为主截面顶角很小的光楔，假定棱镜对光束的偏转矢量与入射光束方向无关，其大小恒定且只由棱镜的顶角和折射率决定，则两个棱镜的光束偏转角可表示为［28］

式中，δ1和δ2为棱镜的光束偏转角，β1和β2为棱镜的顶角，n1和n2为棱镜的折射率。设双棱镜的旋转中心轴为z轴，在垂直于z轴的平面上建立直角坐标系，水平方向为x轴，垂直方向为y轴。假设偏转矢量的方向永远朝向主截面的底边，对于沿z轴传输的光束，可以得到偏转光束在xy平面上的投影，如图1。

图1 双棱镜光束偏转示意Fig.1 Schematic of beam deflection by double prism

图中z轴即为双棱镜的中心光轴，为棱镜的偏转矢量，其大小分别为δ1和δ2，当棱镜旋转时，两偏转矢量将分别以O和O1为中心形成圆锥型的光束偏转范围。总偏转矢量是由每个棱镜的偏转矢量叠加而成，则总偏转矢量在x轴和y轴上的投影，既横向偏角和纵向偏角分别为

式中，θ1和θ2分别为两个棱镜绕z轴的旋转角度，则总偏转矢量可以通过以下两个角进行描述

式中，ρ表示垂直于z轴的光束径向偏离角，φ表示沿z轴的光束轴向旋转角，Δθ=θ1−θ2表示双棱镜夹角。可以看出径向偏离角仅与双棱镜夹角有关，当Δθ=0时出现最大径向偏离角ρ=δ1+δ2，同理当Δθ=π时有最小径向偏离角ρ=|δ1−δ2|。

此时可以在已知棱镜转角的情况下计算出射光束的偏转方向，为了进一步实现指定的光束偏转，还需要在已知目标方向的情况下获取棱镜的旋转角。对于已知δ1和δ2，当给定光束径向偏离角和轴向旋转角时，等价于横向偏角和纵向偏角已知，则根据余弦定理可得两个棱镜各自的偏转矢量与光束总偏转矢量间的夹角为

通过图1可以看出，对于任意目标位置，存在两组可逆的棱镜转角，它们以总偏转矢量为对称中心分布在两侧，则双棱镜的两组期望旋转角可表示为

1.2 双棱镜的旋转非线性分析

当双棱镜的结构参数相同时，可以避免偏转角出现盲区，则有δ1=δ2=δ，此时的光束偏转范围为锥角为ρ=2δ的圆锥范围。在理想情况下，双棱镜系统能够指向其最大光束偏离角绕光轴旋转所成圆锥所包围的任意角度位置，但在对应不同偏转矢量与所需要棱镜转动间存在非线性关系。设δ为7.5°，图2展示了光束径向偏离角随双棱镜夹角的变化关系。

图2 光束径向偏离角随双棱镜夹角的变换关系Fig.2 The transformation relationship between the radial deviation angle and the included angle of the prism

从图中可以看出，当Δθ=π时ρ=0，ρ与Δθ具有近似线性关系。随着Δθ减小，光束逐渐偏离中心光轴，当Δθ=0时ρ=15，ρ与Δθ的非线性愈发明显。可以发现，光束径向偏离角在大部分区域与双棱镜夹角具有较好的线性关系，但是当光束径向偏离角接近于到达极限时，这一关系的非线性特征变得格外明显。根据双棱镜模型，当径向偏离角较小时，对于特定的目标运动时，会出现需要的棱镜的转速和角加速度急剧增大的情况，以目标在光轴附近做匀速的纵向直线运动为例进行分析，图3所示的是跟踪过程中目标运动对双棱镜旋转的影响。

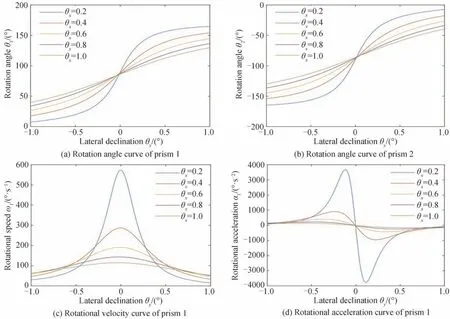
图3 跟踪过程中目标运动对双棱镜旋转的影响Fig.3 The influence of target motion on the rotation of the biprism during the tracking process

如图3，目标的纵向运动速度为2°/s，在θy逐渐接近0的过程中，随着θx的减小，棱镜的转动范围增大，此时棱镜的转速和角加速度也将迅速增加，且随着运动轨迹靠近中心光轴，转速和角加速度的突变越剧烈，在控制器的控制作用不变的情况下，这一情况将使控制精度下降。在这种情况下，双棱镜难以做出及时响应，致使出射光线无法准确指向目标位置，这会导致跟踪误差增大。当θx无限接近0时，将需要棱镜转速无穷大，此时无法进行跟踪。根据上述分析，当目标靠近中心光轴或视场边缘时，棱镜旋转的非线性问题将对光轴偏转性能造成严重影响，跟踪过程中需要尽量远离视场中心和边缘地带，以尽可能降低非线性区域的影响。

2 双棱镜复合跟踪技术

2.1 双棱镜复合跟踪方案

设计了如图4所示的双棱镜复合跟踪系统，采用两个能够独立旋转的折射棱镜组成光束偏折机构，每个棱镜在伺服电机的带动下旋转，并由编码器测量旋转角度，光轴偏转经过矢量叠加后形成一个圆锥形的光束控制范围。在双棱镜跟踪系统中，跟踪性能的限制因素主要有两点，一是棱镜的控制精度，二是视轴的调整误差。前者可以通过改进控制器来解决，对于后者，由于双棱镜的模型误差将耦合到光轴误差中，为解决这一问题，在双棱镜的后方增加一个电磁式快速反射镜来修正光轴，经过棱镜的光束由快速反射镜进行二次偏转，最终到达探测相机视场中心。

图4 双棱镜复合跟踪系统Fig.4 Double prism compound tracking system

其中，旋转双棱镜负责大范围的光轴调节，系统中加入了一个大视场的观靶相机以便于搜索目标位置和光轴初始对准。快速反射镜用于补偿双棱镜的光束控制误差，跟踪相机作为系统中的目标探测元件，用于实时获取光轴的瞄准误差。惯性测量单元（Inertial Measurement Unit， IMU）安装于光学基台上，不同于传统二维伺服转台，由于旋转双棱镜系统特殊的结构和光束偏转机理，无法像传统二维伺服转台一样，通过轴上陀螺反馈实现光轴稳定，因此需要通过姿态解耦以实现对光轴的动态补偿。

2.2 双棱镜的光轴扰动解耦与补偿

双棱镜系统在跟踪过程中，光学基台的姿态扰动会耦合到偏转光轴中，导致跟踪精度下降。不同于传统二维伺服转台，由于旋转双棱镜系统特殊的光束偏转机理，无法像传统二维伺服转台一样利用轴上陀螺反馈实现光轴稳定，因此设计了双棱镜系统的捷联前馈稳定方案以补偿光轴扰动，提高跟踪精度。

根据几何约束可以得到光学基台到偏转光轴的角速度耦合约束关系为

式中，θx，θy为双棱镜的出射光束的方位角和俯仰角。考虑到双棱镜系统的二维偏转特性，设双棱镜的出射光轴在方位和俯仰的等效补偿量分别为ωx，ωy，则有

式中，ω1和ω2分别为棱镜1与棱镜2的转速。在补偿扰动的过程中，双棱镜旋转所产生的光轴偏转会随着姿态扰动一起耦合到光轴运动中，此时有

式中，ωox，oy，oz为光轴的空间扰动，由于ωox对应了光束的轴向转动，其作用等效于目标旋转，而ωoy和ωox对应了光束沿俯仰和方位方向偏转速度，因此需要令ωoy=ωox=0以实现光轴稳定，则双棱镜旋转轴上的等效补偿量为

2.3 双棱镜跟踪控制器设计

双棱镜系统在跟踪目标时，不但需要给出准确的偏转指令，还需要控制器能够尽可能减小出射光轴与目标间的偏差。对于双棱镜系统，由于光轴耦合的特点要求两个棱镜的控制性能完全一致，而模型参数不确定及外部干扰等问题严重降低了光束偏转性能，为改善双棱镜的控制性能，设计了一种改进自抗扰内模控 制 器（Internal Model Control Phase Lead Active Disturbance Rejection Controller， IMC-PLADRC）（如图5），并融入了扰动解耦与补偿环节，以提高动态跟踪性能。

图5 双棱镜跟踪控制器Fig.5 Double prism tracking controller

根据现代控制理论，若系统满足可观性，则可以通过输出和输入信号对其状态进行观测。对于自抗扰控制，将所有与串联积分器不同的动态统一为总扰动，在伺服电机带动下的旋转棱镜的动力学模型可以描述为

式中，b0为控制增益，u为控制信号，f表示外部扰动和未建模动态的总和。则被控对象的状态方程可描述为

式中，h=通过扩张状态观测器可以实现对总扰动的估计和补偿，建立的三阶线性扩张状态观测器可表示为

式中，β1，β2，β3为观测器增益，基于带宽参数化方法对增益配置进行配置，则观测器误差传递矩阵的特征方程为

此时得到观测器增益为

式中，ωo被定义为观测器的带宽［29］。理想情况下当ωo足够大时，观测器能精确的估计总扰动，通过设计合适的控制器即可实现良好的跟踪性能。但现实中ωo显然不可能无限增大，因此观测器对扰动的估计存在滞后，这造成了控制系统性能损失。为改善这一问题，在扰动估计中加入相位超前网络

式中，c为相位调节因子，λ为时间常数。则经过相位校正后的扰动估计项的微分方程为

式中，z3l=F(s)⋅z3，根据观测器方程可得到改进的总扰动估计传递函数为

假设存在总扰动f(t)=At，则观测器的扰动估计可表示为

通过拉普拉斯逆变换得到扰动估计的时域表达式为

当t→∞时，系统的总扰动估计误差为

令e3l(∞)=0，得到时间常数的表达式为

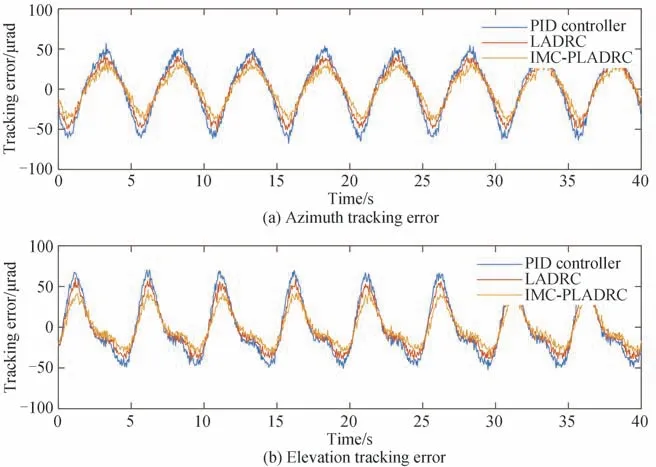
其中相位调节因子c的取值范围为(0，1]，此时时间常数可以随着观测器带宽和相位调节因子的改变实现自动调整，在观测器带宽确定后，相位超前网络中需要调节的参数仅有c，这使参数整定变得非常简单。对于确定的观测器带宽ωo，当c=1时，超前网络的传递函数为1，观测器等效为传统线性扩张状态观测器，当0

在条件允许时应尽可能增加观测器带宽ωo以有效地降低观测器的总扰动估计误差，然而过高的带宽会将高频噪声引入闭环系统，不利于系统的稳定。降低c能够改善扰动估计的响应，减少扰动估计的相位滞后和幅度衰减，但会削弱系统抵抗高频噪声的能力，因此考虑到噪声和采样率的限制，需要根据工程需求对观测器带宽和相位调节因子进行适当选取。

转角控制器采用内模控制框架进行设计，以获取更好的鲁棒性和跟踪性能。经过扰动补偿后的系统模型转化为纯积分器串联形式，此时经过速度闭环后的被控对象名义模型为

式中，k为转速控制器，在保证稳定的条件下应尽量增大k以提高系统响应速度。棱镜系统的转角控制闭环传递函数被期望为低通滤波器形式，设其传递函数为f(s)，则内模控制器可表示为

式中，G−1(s)为被控对象的逆模型，T为快速因子，用于调节控制器的跟踪性能，适当减小T将有助于减小跟踪误差。改进的控制器极大地简化了控制系统的设计难度，做到双棱镜控制性能一致，并有效提高跟踪性能。

3 实验与结果分析

为验证所提出的基于旋转双棱镜的光束复合跟踪性能，搭建了如图6所示的实验验证装置。棱镜的有效口径为50 mm，选择目标波段为1 053 nm，对应的双棱镜最大径向偏离角为15°，考虑到棱镜的色散效应，不同波长的光束穿过双棱镜系统后，传播方向会发生不同程度的偏折，因此在光路中通过镀膜和设置窄带滤光片以过滤杂散光。棱镜的转动角度由各自的光电编码器采集后反馈到棱镜控制器中形成闭环，跟踪相机视场为3 mrad，输出帧频为200 Hz。采用STM32F4型MCU作为主控制单元，闭环控制采样周期为1 ms。惯性测量单元安装于光学基台上，并通过光学标校保证其坐标轴与双棱镜的中心光轴重合，以保证扰动解耦的准确性。电磁式快速反射镜具有二维的偏转自由度，角分辨率≤1 μrad，线性度≥99.80%，与光学系统适配后的单轴偏转行程为2°，闭环伺服带宽为500 Hz。其偏转角度实时传递给视轴解算单元用于修正双棱镜的旋转角度。

图6 复合跟踪实验系统Fig.6 Compound tracking experimental system

在沿旋转双棱镜的中心轴线方向使用准直器产生近似平行光以模拟远距离目标，旋转双棱镜系统固定在六自由度摇摆台上，用于模拟动基座平台的姿态扰动。实验开始前，控制双棱镜进行光轴指向以保证光斑进入视场，考虑到视场中心和边界的非线性效应，将初始径向偏离角−9°，轴向旋转角0°的位置设定为跟踪中心。

在动态跟踪实验中，通过摇摆台输入姿态扰动幅值为5°，频率为0.2 Hz，以模拟动基座条件下的目标跟踪。图7展示了改进自抗扰内模控制器与传统比例-积分-微分（Proportion Integral Differential， PID）控制器以及线性自抗扰控制器（Linear Active Disturbance Rejection Control， LADRC）的双棱镜控制精度对比。

图7 双棱镜的转角控制误差Fig.7 Angle control error of double prism

可以看出，采用改进自抗扰内模控制器的双棱镜转角控制误差最小，其控制精度明显优于PID控制器和线性自抗扰控制器。当采用传统PID控制器时，棱镜1和棱镜2的控制误差分别为0.50 mrad与0.49 mrad，当采用线性自抗扰控制器时，棱镜1和棱镜2的控制误差分别为0.31 mrad和0.31 mrad，而采用改进后的自抗扰内模控制器时，棱镜1和棱镜2的控制误差分别降低为0.21 mrad和0.21 mrad。改进自抗扰内模控制器相较于传统PID控制器以及线性自抗扰控制器的平均控制精度分别提高58.33%和32.81%。控制精度的提高能有效改善双棱镜系统跟踪精度。图8展示的是没有视轴补偿的情况下，通过改进控制器带来的跟踪性能的提升。

图8 双棱镜系统的光轴跟踪误差Fig.8 Optical axis tracking error of the double prism system

可以看出，改进自抗扰内模控制器使双棱镜的跟踪精度明显提高，采用传统PID控制器时方位轴的跟踪误差为34.44 μrad，俯仰轴的跟踪误差为34.91 μrad，合并两轴的误差得到总跟踪精度为49.03 μrad。采用线性自抗扰控制器时方位轴的跟踪误差为27.24 μrad，俯仰轴的跟踪误差为27.75 μrad，合并两轴的误差得到总跟踪精度为38.88 μrad。当采用改进自抗扰内模控制器后，方位轴的跟踪误差为22.07 μrad，俯仰轴的跟踪误差为21.98 μrad，合并两轴的误差得到总跟踪精度为31.15 μrad。在此基础上，开启快速反射镜对双棱镜进行视轴补偿，图9为加入视轴补偿前后的双棱镜系统跟踪误差对比。

图9 双棱镜的复合跟踪误差Fig.9 Compound tracking error of the double prism

开启视轴补偿后，双棱镜系统进入复合跟踪模式，其跟踪精度进一步提高。其中，方位轴跟踪误差由22.07 μrad减小到5.43 μrad，俯仰轴跟踪误差由21.98 μrad减小到5.16 μrad，总体复合跟踪精度为7.49 μrad，相较于补偿前提高4.16倍。

4 结论

通过开展基于旋转双棱镜的光束复合跟踪控制技术研究，建立了旋转双棱镜的光束偏转模型，详细推导了光束总偏转矢量与双棱镜转角间的关系，分析了双棱镜在目标跟踪过程中的非线性问题。设计了光束复合控制系统，引入快速反射镜对双棱镜的光轴误差进行实时修正，通过建立双棱镜光轴与光学基台间的扰动耦合关系，实现对了双棱镜光轴的捷联稳定，并设计了一种改进自抗扰内模控制器以改善棱镜的控制性能。在此基础上搭建了实验系统，对基于旋转双棱镜的光束复合跟踪技术进行验证。实验结果显示，改进的控制器能明显提高双棱镜的控制精度，相较于采用PID控制器和线性自抗扰控制器时双棱镜的平均控制误差分别减小58.33%和32.81%，并使动态跟踪误差由采用PID控制器和线性自抗扰控制器时的49.03 μrad和38.88 μrad降低为31.15 μrad。开启视轴补偿后跟踪性能进一步提高，总跟踪误差减小至7.49 μrad，相较于补偿前跟踪精度提高4.16倍。双棱镜复合跟踪系统所展现出优异性能，验证了双棱镜控制技术的正确性和有效性，为基于旋转双棱镜的小惯量伺服技术的发展提供实验参考与理论支持。后续研究将继续深化对于旋转双棱镜跟踪系统的改进，继续优化跟踪性能。考虑到视轴补偿在复合跟踪中的重要作用，针对以快速反射镜为核心的精跟踪单元的优化也是未来的重要工作之一，通过调整光路结构，改进硬件电路的设计，优化控制流程以及采用更高性能的跟踪相机等方法将有助于进一步提高复合跟踪精度。