基于特征圆靶的单目视觉位姿测量算法研究

丁江，宋朝成，，马翠，何凯，左启阳

（1 广西大学 机械工程院， 南宁 530004）

（2 中国科学院深圳先进技术研究院， 深圳 518055）

0 引言

随着工业机器人［1-2］的应用越来越广泛，基于机械臂的自动锁螺丝机器人［3］，室内喷涂机器人［4］，缺陷检测机器人［5］等的精度需求也越来越高，其中机械臂与工作平面的相对位姿的准确度往往是最为关键的一环。而圆作为生活中常见的几何特征，往往多出现于各种物体和工件之上。鉴于单目视觉位姿测量［6］较于双目、多目，具有结构简单，系统运算量低等优势，故研究基于平面圆特征的单目视觉系统下空间平面相对位姿的求解将具有重要意义。

目前空间平面位姿求解主要分为多点约束问题和非点约束问题。前者主要有FISCHLER J等［7］在1981年提出的基于点约束的多点透视问题（Perspective n-points Problem， PnP），通过解析法和迭代法等可精确求解目标位姿，计算较为复杂；LEPRTIT V 等［8］提出的高效率多点透视（Efficient Perspective n-points Problem，EPnP）算法在能获得高质量图像的前提下大大提升了PnP算法效率；陈鹏等［9］在EPnP算法基础上提出的基于迭代的高效率多点透视（Iterative Efficient Perspective n-points Problem，IEPnP）算法，在对噪声的高鲁棒性下保持了EPnP算法的高效率。作为非点约束的基于平面圆特征的位姿测量研究因其靶标制作简易，原理简单，也引起了广大学者的注意。其基于是否考虑空间圆的透视畸变，又可分为考虑透视畸变的类椭圆方法和不考虑透视畸变的椭圆法。如KABUKA M和ARENAS A［10］把圆投影图视作椭圆，提出了将投影椭圆短径与长径比值来作为目标平面的俯仰角，并通过目标靶面的投影阴影来消除姿态解的二义性。ZHOU Z等［11］在正投影的前提下通过圆形标记实现了对物体的三维识别。SHIU Y C和AHAMED S［12］提出了既能处理球形特征，又能处理圆形特征的方法，并给出了封闭解。SAFAEE-RAD R等［13］基于圆形特征的三维位置估计推导出了封闭解析解，提供了一种针对球面特征的封闭解析解方法，并做了仿真和实验验证。ZHANG G和WEI Z［14］建立了用于透视投影的椭圆中心位置畸变模型，提高了空间圆的定位精度。何森等［15］在考虑透视畸变的情况下完成了单目视觉的非接触式飞机舵面角位移标定，但对标靶尺寸精度要求较高，坐标转换中间误差较大，依赖于准确的距离测算。WANG G等［16］以更少的条件参数提出并证明了从一个圆和两对平行线的单一图像中恢复相机姿态的可能性。ZHENG Y等［17］给出了圆的投影方程，在此基础上提出了单目圆位姿估计的闭合形式解，并从几何角度说明了这两种可能解集的合理性以及它们之间的关系。张磊等［18］设计了空间圆投影仿真模型，并增加了激光测距仪来获取深度信息；魏振忠等［19］通过圆和共面的直线对，基于欧氏空间中的角度不变量消除了圆特征姿态计算结果的二义性；苗锡奎等［20］通过引入额外参考点的方式消除了空间圆求解的二义性。LIU L等［21］在考虑透视畸变的前提下推导了空间圆姿态求解方程，但是对图像采集及处理要求严格，鲁棒性较低。李志宇等［22］研究出一种基于线结构光传感器的圆位姿测量方法，扩展了线结构传感器测量圆孔位姿的适应性。于长志等［23］借助排列点激光位移传感器提出了背靠视觉端面对接定位方法，进一步提升了空间圆位姿求解精度。

由于上文所述研究大多涉及较远距离下的空间平面位姿求解，对近距离下的适用性还有待研究。如在目标圆靶大小不变时，近距离下透视投影带来的“近大远小”透视畸变将不得不被重视，其主要表现为圆在相机中的成像为一个类椭圆，而不是一个标准椭圆。此时仍然将其投影成像当作椭圆来处理，必然带来相应的误差。本文设计了一种圆形标靶和基于平面圆特征的单目视觉位姿测量算法。在考虑透视畸变的前提下，经过误差分析和实验验证，该算法具有更高的精度，满足近距离测量要求，通过将其和现有算法的配合使用，可以提高空间平面位姿的整体求解精度。

1 靶标的设计和相机成像原理

如图1所示，本文设计了一种可用于求解机械臂末端与目标平面相对位姿的圆形标靶。该标靶主要由一个同心圆环，三个圆以及一个三角形组成。其内部特殊的图案组成，可实现对靶标圆心的准确定位，且在相机光轴与目标平面垂直时仍然可以推导出标靶绕其法向量的旋转角度。因本文主要研究空间平面与相机的相对俯仰角问题，其余问题在此不做叙述。

图1 特征圆靶Fig 1 Characteristic circular target

在单目相机成像原理中，主要涉及三个坐标系。通过右手螺旋定则可建立如图2所示的空间坐标位置关系，包括以相机光心为坐标原点的相机坐标系OcXcYcZc，与相机坐标系Z轴同向，X，Y轴相互平行的图像坐标系O2X2Y2Z2，以及位于目标平面上的世界坐标系O3X3Y3Z3。空间平面与相机的位置关系即变成了相机坐标系与世界坐标系之间的转换关系，在像平面X，Y坐标轴完全垂直时，此转换关系可用式（1）表示。

图2 相机成像原理Fig.2 Camera imaging principle

式中，Zc为相机光心与目标点的垂直距离，即目标的深度值，K为相机标定获得的内参矩阵，R和T同样由相机标定获得，分别代表旋转矩阵和平移矩阵。经标定后，本文所用相机的内参矩阵和畸变系数分别如式（2）、（3）所示。式（3）中k1，k2和k3为径向畸变系数，p1和p2为径向畸变系数。此后计算所用图片均已消除畸变。

2 算法实现

2.1 算法原理

基于相机成像中的透视投影原理，建立如图3所示的投影关系示意图。为了方便理解和计算，本文取目标中心与相机光轴共线时的相对位置来对算法进行说明和仿真实验。

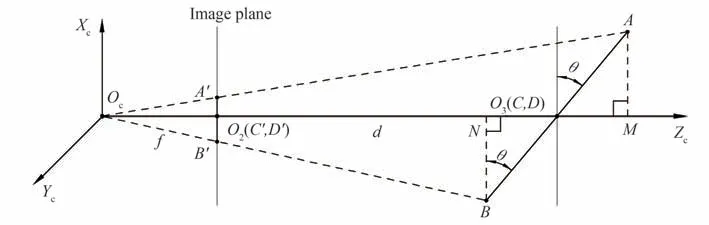
图3 透视投影原理Fig.3 perspective projection principle

图3中相机坐标系原点Oc与图像平面中心O2的距离为焦距f，相机坐标系原点Oc与目标圆靶中心O3的距离为d，即物距。AB长度为目标圆靶的直径2r。从AB两点向Zc引垂线分别交Zc于点M，N。由三角形相似关系ΔOcO2B＇∽ΔOcNB和ΔOcO2A＇∽ΔOcMA可以得到

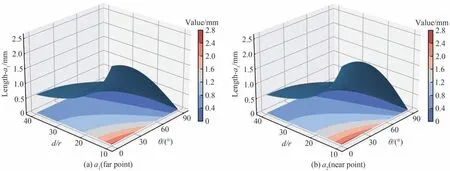
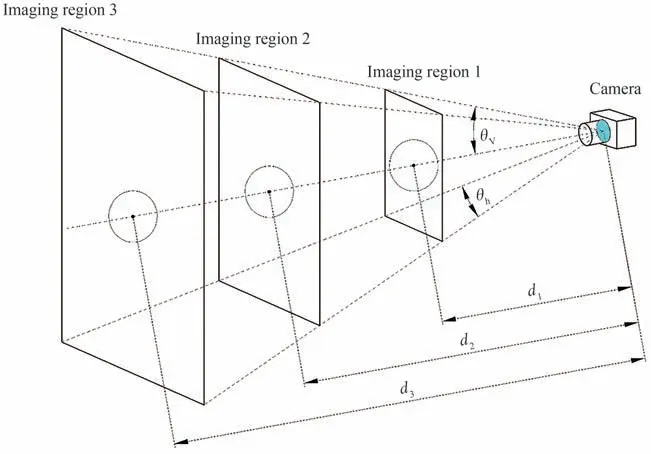
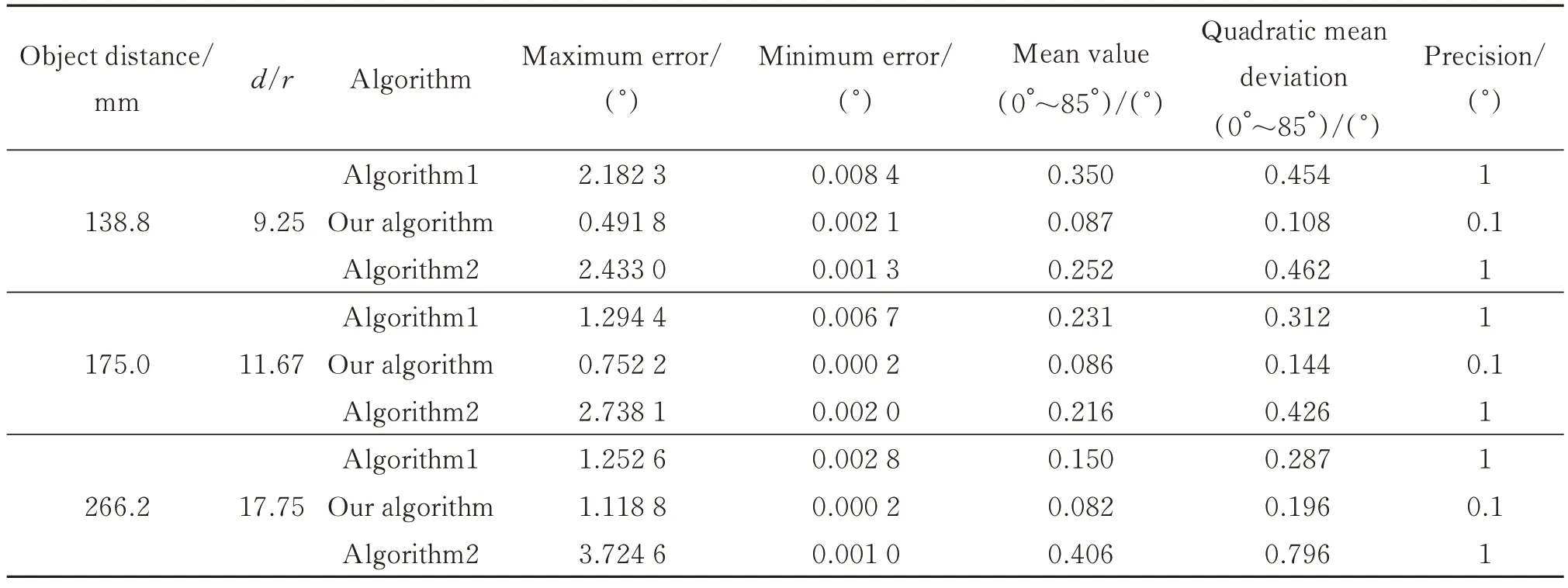
式中，a1，a2分别为目标圆成像中类椭圆短轴的两部分长度，且a1

图4 圆靶投影示意图Fig.4 Schematic projection of a circular target

再根据三角形角度关系

联立式（4）～（6）可以得到以远点（点A）和近点（点B）的结果θ和θ＇分别为

当目标圆靶与相机光轴OcZc垂直时有

式中，b为该物距下目标圆靶直径所对应的其在图像坐标系中的长度，单位mm，为消除物距测量和标靶制作误差，将式（9）分别代入式（7），式（8）可得

此时，俯仰角θ的计算只同图4中的a1，b以及定值f相关。因为目标圆靶与相机坐标系所在平面XcYcZc的夹角θ范围在0～90°，所以角θ的正弦值必然为正。由式（11）可以看出，当以近点（点B＇）来计算时，可能存在两个正解。这在实际测量中，由于相机装配误差和成像的像素误差等的存在，这个现象将更加普遍，这便出现了同目标圆成椭圆像时的二义性相似的问题。所以本文采用的是三点算法，即目标圆成像中类椭圆长径的两个端点（点C＇和点D＇）和短径的远点（点A＇），此处的远点仅代表短径的短边部分的端点。

为了进一步说明特征点的选取依据，联立式（4）、（5）可得

取相机焦距f为25 mm，式（12）可用图5表示如下。从图5中的等高线也可以看出当目标圆靶直径确定时，随着物距的减小，a1由θ改变引起的长度变化相对a2更加显著，特别是θ较小时更为明显。这对角度变化的测量更加有利。

图5 透视畸变下a1和a2长度的变化Fig.5 Variation of a1 and a2 lengths under perspective distortion

在对图形进行二值化，去噪，消除尖锐凸点和断点的开闭运算等形态学处理后，通过canny［24］算子检测边缘并基于文献［25］中的二值化图案轮廓提取方法来提取圆靶外圆轮廓，且后续关键点的提取以及椭圆拟合均是基于此轮廓的计算。通过计算可以得出轮廓中距离最远的像素点对C＇（u1，v1）和D＇（u2，v2），以C＇D＇连线（式（13））为基准，统计直线两侧轮廓点集的大小。根据透视投影中近大远小的原理，点集相对较小的即为远点所在轮廓。再通过求解此点集中距离直线C＇D＇最远的点即为所求远点（u0，v0），此点在图4中表现为点A＇。进而由式（10）求出目标圆靶所在平面相对于相机的俯仰角大小。最后借助点与直线位置关系判别式（式（14）），以远点位于直线C＇D＇上侧还是下侧作为俯仰角的方向。目标平面的偏转角则由直线C＇D＇的斜率求得，至此即可唯一确定目标平面的旋转姿态。

2.2 其他算法

本文选择目前较为主流的椭圆法（算法1），以及同样考虑透视畸变的另一种类椭圆方法（算法2）。

算法1因不考虑透视畸变，故一般应用于较远距离下空间平面的位姿求解，即默认d/r≫sinθ，此时式（12）将被改写成

联立式（9）和式（15）可得

算法1是目前主流的基于特征圆的空间平面位姿求解依据。值得注意的是d/r这个尺度什么时候可以判定为远大于sinθ，并没有明确的研究数据参考。为此本文取相机焦距f为25 mm，目标圆靶半径r为15 mm，相机像元尺寸为2.4 μm。不考虑像元尺寸在成像平面XY两个维度的尺度偏差，并将透视畸变下目标圆靶的倾斜角度作为真值，并以最大误差来代表每一个d/r值下该算法的绝对误差，结果如图6所示。在将d/r≤16.9视为近距离时，椭圆法的精度为1°，在16.9≤d/r≤53.5时精度可以提升到0.1°。显然，这对于工业相机的近距离精密测量来说是不可忽视的。此外椭圆法的解集存在二义性［7-8］，需要增加外设和算法来消除。其中最常用的是通过求解成像椭圆方程，获得其椭圆锥面方程，进而反推出目标圆靶所在平面的平面方程，最后确定唯一解。整个算法需要知道目标圆靶的尺寸r，在r未知时，主要通过式（9）来实现对目标圆靶尺寸半径r的测量，对于机械臂平台来说，可以通过机械臂在坐标轴方向的两次平移来实现单目视觉下深度信息d的获取。

图6 椭圆法绝对误差变化Fig.6 The variation of absolute error accuracy of ellipse method

算法2可由式（4）和式（5）联立得到如式（19）所示关系，由a1与a2大小关系，可直接求得带符号的角θ值，并通过θ的正负来判断角θ方向。此方法依赖于对类椭圆短径两部分的求解，在目标圆靶与相机光轴共面时a1与a2的和为0，方程无解，导致大角度测量时精度将受影响。

3 误差仿真计算

由于沿摄像机光轴方向上的位移测量精度一般远低于垂直光轴方向上的位移测量精度［26］，在相对位姿测量中主要表现为俯仰角测量精度小于偏转角测量精度，且不同算法之间的区别主要为空间圆成像中短轴长度的测量。因此为了方便比较三种方法的差异，本文仅计算误差较大的空间平面俯仰角θ值的大小，其方向的判定不影响对精度的验证。在基于工业相机和特征标靶的单目视觉近距离测量中，图像的处理和识别是影响整个系统精度的主要因素。外界环境如光照、标靶表面环境等往往表现为图像采集质量的优劣，相机及外部设备的安装精度虽然难以避免，但本文求解的是目标平面与相机坐标系的相对姿态，故机械安装误差并不影响求解精度。在以像素为单位的视觉测量中，对目标像素尺寸的处理与计数直接关乎目标在空间位置的物理尺度，考虑到近距离测量相对远距离图像质量较高，故此处分别取0.1个和1个像素做误差干扰分析。

因为像素测量的不确定性在符号相反的时候表现最强烈，且不同算法均涉及对目标圆靶成像的长径和短径的测量，故以θ0为真值时可得算法1的误差模型为

本文算法和算法2的误差模型e1，e2为

式中，n为误差像素个数，Lpixel为相机的像元尺寸，a1，a2由θ0代入式（4）和式（5）得到。

本文第三节实验部分主要涉及d=138.8 mm，d=175.0 mm，d=266.2 mm三个不同物距下的计算，此处为与后续实验部分贴合，分别仿真计算了n=1和n=0.1时三个d/r值下的误差，结果如图7所示。

图7 不同算法的绝对误差变化（r=15 mm）Fig.7 Absolute error variation of different algorithms （r=15 mm）

从图7中可以看出，随着距离和误差像素的增加，三种方法的误差大小均出现了增加，其中算法1的误差变化与文献［6］中的趋势一致，说明本文误差分析方式的正确性。值得注意的是，本文算法随着物距增加，其误差曲线逐渐接近算法1，两者的差值由图中的阴影部分表示。本文算法与算法1的误差曲线主要表现为随着角度的增加逐渐减小的趋势，且误差在20°以内变化最为显著；算法2则正好相反，其误差在70°～90°变化最为显著。从图7综合来看，相对于其他两种方法，算法2误差变化幅度均较大。

4 实验验证

由于误差仿真是在圆投影图像中长短轴同时发生等量像素误差时的较为理想状态下的计算，为了能更进一步探究三种算法的差别以及验证误差仿真计算的正确性，本文进行了相关实验。实验平台如图8所示，主要包括用于产生相对转角姿态的机械臂以及装配在其上的用于进行图像采集的工业相机，环形光源，视觉实验架，圆点相机标定板，特征圆标靶，待测平板等。所用设备参数如表1所示。

图8 空间平面位姿测量实验平台Fig.8 Experimental platform of spatial plane pose measurement

表1 主要设备Table 1 Main equipment

相机成像中的透视畸变会给目标圆定位带来误差，从而给本文基于相机正对目标圆靶这一前提下的计算造成影响。为保证初始位置相机光轴与目标圆靶中心共线，参考文献［14］和文献［27］中的方法预调节，以降低圆靶定位不准带来的误差。

如图9所示，图中θh和θv分别为相机水平视场角和垂直视场角，成像区域中的圆为目标圆靶。我们发现不同物距下，相机成像区域不同，圆靶在成像区域中的占比也不同。在综合考虑所用相机景深和像元精度，并保证实验过程中相机成像始终可以包含标靶对象的前提下，本文物距最小为138 mm，最大为264 mm，同时取实验平台的设计工作距离174 mm。已知目标圆靶尺寸r=15 mm，三个物距与圆靶半径的比值由图6可知，满足近距离测量的应用。

图9 不同物距下相机的成像区域Fig.9 Imaging region of camera at different object distances

实验过程中，以相机为工具设置机械臂的工具坐标系，并调节机械臂使其工具坐标系原点落在待测平面的圆靶中心。圆定位以及机械臂手眼坐标转换均有相关研究，本文在此不做叙述。为保证初始位置相机光轴垂直于待测平面，即待测平面俯仰角为0°，可通过圆点标定板的位姿来调整。接着操作机械臂示教器进行重定位操作，控制机械臂以工具坐标原点为旋转中心，以工具坐标系X轴（或Y轴）做定轴转动，每转动1°，相机分别采集一张特征圆靶图片和圆点标定板图片。当物距较近视野较小无法同时获得两张图片时，可微调机械臂沿工具坐标系X轴（或Y轴）移动之后反向复位来获得同一旋转姿态下特征圆靶和标定板的图片。因为越接近90°，光源辐射面积减小以及相机景深的影响，图片质量将难以保证。故本文为保证始终获取到较高质量的图片，限制机械臂转角在0°～85°范围内。每个物距下，通过光源调节器适时地调节光源亮度并手动打光，在不同方向和强度的光照下反复测量十次，其测试物距分别为138 mm，174 mm，264 mm，共三组数据。通过将每个俯仰角下标定板在相机中的十次位姿的均值作为该位置待测平面俯仰角的真值，并以此计算各方法的绝对误差。每组数据中测得的物距均值作为改组数据的d值。再以每10°为一组，取其绝对误差的均值及标准差做误差棒，实验结果如图10所示。

结合图7，可以确定本文实验中的像素精度在0.1～1个像素之间。进一步观察图10可以得出：

1）0°～30°时，相对于算法1，本文算法与算法2的误差更小；此区间仿真结果中误差的增大表现为实验中误差波动的增加；随着俯仰角的减小，圆靶的畸变误差降低，测量误差变大，故三种算法的结果误差均逐渐增大且波动加剧；三种算法误差均从接近0开始，是因为本实验以相对俯仰角0°为初值，俯仰角较小时，待测平面与相机光轴接近相对垂直姿态，光源辐射面积更大、更均匀，其图像获取精度更高；对于图10 （a）～图10 （c）中的曲线与仿真结果略有差异，主要是实际测量受限于硬件设备、光照、标靶精度等客观因素，而仿真基于的是像素误差呈对称分布时的最大化数值计算的。

2）30°～50°时，三种算法误差降低的趋势均趋向平缓，且能保持较高的精度；不同物距下各算法的绝对误差变化与上节的误差仿真计算曲线相似。

3）50°～90°时，本文算法与算法1的误差进一步降低，且逐渐趋于平缓；三种算法得到的实验结果与仿真计算曲线相似；从图10 （e）～ （f）的误差棒可以看出，算法2因受累积误差影响，相较于与其他两种算法，其误差大小和波动均逐渐增加；随着物距增加，算法2误差开始增大的起点角度越来越小。

图10 不同算法绝对误差的实验结果（r=15 mm）Fig.10 Experiments of absolute error based on different algorithms （r=15 mm）

为比较三种算法的整体误差，统计分析了各组数据结果，如表2所示。由表2数据可得，本文算法在三种预设条件下，平均精度均可以精确到0.1°，且数据波动均最小。

表2 三种算法统计结果（r=15 mm）Table 2 Results of three algorithms （r=15 mm）

5 结论

以基于机械臂的单目视觉系统为平台，研究了近距离测量时由特征圆靶来求解空间平面姿态角的问题，主要涉及空间平面姿态中俯仰角大小的测量，在考虑透视畸变的前提下，通过透视投影原理提出了三点求解空间平面俯仰角的算法，与本文中同样考虑透视畸变的算法2相比，参数更少；与其他算法相比，在对图像进行去噪、形态学处理后，本文算法拥有更高的精度，误差在0.1～1像素时，可以精确到0.1°；在保证目标圆靶位于图像中心时，目标圆靶尺寸不直接参与本文算法计算，可有效避免靶标制作精度带来的误差；根据主流的不考虑透视畸变的椭圆算法（算法1）的固有误差变化曲线，相机物距与目标圆靶半径的比值在大于17时可近似忽略透视畸变带来的算法误差。下一步将进行更多环境下的实验测量，引入亚像素来提升算法的精度，并研究误差变化，同时优化算法，以提升鲁棒性和检测效率。