石墨烯表面涡旋光束的局域动力学特性分析

马万琦，崔志伟

（西安电子科技大学 物理学院， 西安 710071）

0 引言

近年来，石墨烯因具有优异的光学、电学和力学特性而受到了国内外研究学者的广泛关注［1-3］。石墨烯是由单层碳原子紧密堆积成二维蜂窝状晶格结构的一种碳质新材料，其电导率由费米能量决定，而电导率通过施加偏置电压或外部电场在较宽范围内进行调谐［4］。石墨烯一个独特的性质是其反射特性由精细结构常数和本征参数决定［5-6］，这些参数通过静电掺杂改变费米能级来进行调制［7-9］。石墨烯的这种电光调制效应作为增强光与物质相互作用的新手段［10］，对于理解电磁波和光在石墨烯表面的反射特性有着非常重要的作用［11-12］。MERANO M推导得到了石墨烯的菲涅尔系数［13］，并基于该系数研究了石墨烯表面反射高斯光束的Goos-Hänchen（GH）位移和Imbert-Fedorov（IF）位移［14］。随后，ZHUO Linqing等研究了石墨烯表面反射涡旋光束的IF位移［15］，结果表明，通过调节石墨烯的费米能量，可有效控制涡旋光束的IF位移。

另一方面，涡旋光束由于其独特的物理性质和新颖的物理效应及其极具潜力的应用前景也受到越来越广泛的关注，已成为光学和光电子学领域的研究热点之一［16］。作为一种特殊形式存在的电磁波，具有特定振幅、相位和偏振态分布的涡旋光束不仅具有能量，而且具有动量和角动量。角动量包括由偏振螺旋决定的自旋角动量和由相位螺旋决定的轨道角动量。能量、动量和角动量作为描述涡旋光束与物质相互作用过程中局域动力学特性的几个重要物理量，有助于揭示物质新的物理效应和特性。国内外众多学者已对自由空间中以及聚焦情况下涡旋光束的能量、动量和角动量进行了深入研究［17-22］。CUI Zhiwei等研究了涡旋光束反射和折射情况下的局域动力学特性［23］。本文对石墨烯中涡旋光束局域动力学特性进行了研究。

1 理论模型

如图1所示，考虑涡旋光束从空气入射到石墨烯-衬底系统表面的反射，设空气中的折射率为n0，石墨烯衬底的折射率为n1。石墨烯-衬底分界面位于全局坐标系(x，y，z)中，z轴垂直于分界面并指向石墨烯衬底，位于衬底顶部的单层石墨烯在z=0的位置，沿z轴方向施加静磁场B。(xi，yi，zi)和(xr，yr，zr)分别表示入射光束坐标系和反射光束坐标系，θi和θr分别表示中心波矢量的入射角和反射角。

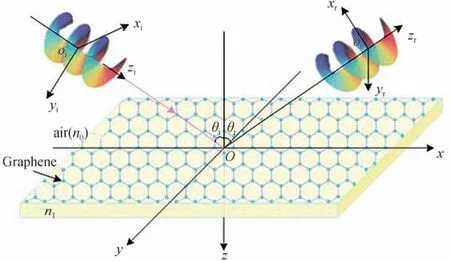
图 1 涡旋光束从空气入射到石墨烯-衬底系统表面反射示意图Fig.1 Illustration of the reflection a vortex beam illuminating from air onto the surface of a graphene-substrate system

1.1 石墨烯界面的菲涅尔反射系数

对于如图1所示的石墨烯-衬底系统，根据边界条件，可得到石墨烯界面的菲涅尔反射系数为［24］

1.2 石墨烯表面反射涡旋光束的矢量分析

众所周知，满足傍轴近似方程的拉盖尔-高斯（Laguerre-Gaussian，LG）光束是一种典型的涡旋光束。当径向模数p=0时，在坐标系(xi，yi，zi)中，zi=0处拉盖尔高斯涡旋光束的标量角谱表达式为［23］

式中，l为LG涡旋光束的角向模数，也称为拓扑荷数，w0为光束初始平面处的束腰半径，kix和kiy分别表示波矢ki在x和y方向的分量，ki=k0=2π/λ0为光束在自由空间中的波数，λ0为入射光束的波长。利用坐标系之间的变换，得到反射涡旋光束在坐标系(xr，yr，zr)中的角谱表述［25］

为了在布儒斯特角附近获得较为准确的结果，将菲涅尔反射系数rmn(m=p，s；n=p，s)在kix=0处作泰勒级数展开并取一阶近似，施加边界条件kix=−krx，得到［26］

将式（6）代入式（4），忽略二阶项，便可以得到修正后的反射涡旋光束角谱表达式。然后，根据式（7）进行傅里叶变换

得到

其中

式中，kr=k0为反射光束在自由空间中的波数，zR，r=为反射光束的瑞利距离。

在傍轴近似条件下，采用基于洛伦兹规范的矢量势方法，反射涡旋光束的电场和磁场可写为［27］

式中，

1.3 结构光场动力学参量的描述

能量、动量、自旋角动量（Spin Angular Momentum，SAM）和轨道角动量（Orbital Angular Momentum，OAM）作为结构光场几个重要的动力学参量，有助于揭示结构光场和物质新的物理效应和特性。但是对于结构光场动力学参量的描述，基于经典力学和电磁理论建立的机械动力学理论存在着一定的局限性。采用经典的机械动量描述结构光场的动力学特性时缺乏清晰的物理意义，无法对自旋角动量和轨道角动量进行独立描述，不能解释结构光场与物质相互作用时局部动量的传递和光对物质施加的辐射压力［28］。理论研究表明，在量子力学和相对论场论范畴内，采用正则方法建立的光场动力学理论可以很好的解决上述问题。对于均匀各向同性媒质中的结构光场，电磁场对偶形式的能量、正则动量、自旋角动量和轨道角动量密度的定义分别为［28］

式中，E和H为光场的电场和磁场，ω表示光束的角频率，ε和μ分别为光场所在空间中介质的介电常数和磁导率，Im[⋅]表示虚部，上标“∗”代表复共轭，符号A⋅(∇)B定义为A⋅(∇)B=Ax∇Bx+Ay∇By+Az∇Bz。上述定义的正则动量和角动量具有清晰的物理解释，即动量密度与场相位的局部梯度成正比；自旋角动量密度是光场的内禀属性，与光场的偏振态有关；轨道角动量与光场的传输路径和空间相位结构有关。

2 结果分析

将式（12）和（13）代入式（22）～（25），编写程序进行数值模拟，分析石墨烯表面涡旋光束的局域动力学特性。本文着重分析光束的入射角和拓扑荷数，以及石墨烯-衬底系统的费米能量和磁场对涡旋光束在石墨烯表面反射后局域动力学特性的影响。若无特殊说明，计算参数取值为：涡旋光束的波长λ0=632.8 nm，拓扑荷数l=2，束腰半径w0=1.0λ0，极化参数(α，β)=(1，i)/，入射角θi=45°；石墨烯衬底的折射率n1=1.517，费米能量μF=0.25 eV，费米速度vF=1×106m/s，电子电量e=1.6×10−19C，磁场强度B=6T；观察平面所在位置zr=λ0，观察点坐标为xr=yr=λ0。

图2是入射角对涡旋光束在石墨烯表面反射后能量、动量、自旋角动量和轨道角动量密度的影响分布，其中θi=59.1°为布儒斯特角。从图中可以看出，随着入射角的增大，能量密度和动量密度呈现出相似的变化规律。能量、动量、自旋角动量和轨道角动量密度分布在布儒斯特角附近均发生了突变。当入射角小于布儒斯特角时，能量密度和动量密度呈现出环形的非均匀分布，而当入射角大于布儒斯特角时，能量密度和动量密度逐渐呈现出月牙形的轮廓。相较于能量、动量和轨道角动量密度，自旋角动量密度呈现出完全不同形状的轮廓，且入射角的改变对自旋角动量密度的影响较为显著。当入射角增加到θi=75°时，自旋角动量呈现出与其它动力学特性量类似的月牙型分布。当入射角小于布儒斯特角时，轨道角动量密度呈现出环形分布，峰值强度的位置随着入射角的改变呈现出较大变化。

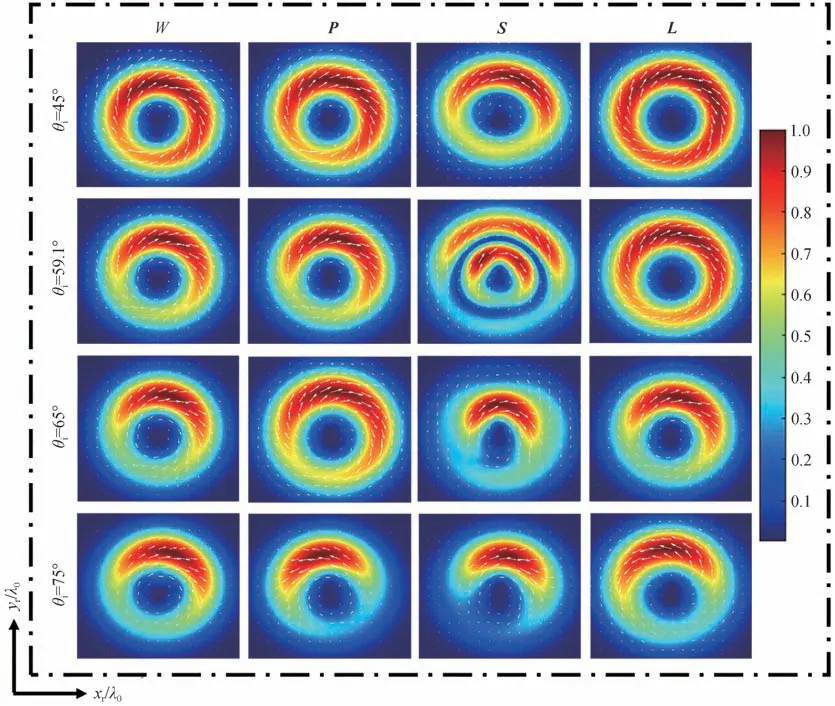
图 2 入射角对涡旋光束在石墨烯表面反射后能量、动量、自旋角动量和轨道角动量密度的影响Fig.2 Effect of the incident angle on the energy， momentum， SAM and OAM densities of the vortex beams reflected from a graphene-substrate interface

图3是拓扑荷数对涡旋光束在石墨烯表面反射后能量、动量、自旋角动量和轨道角动量密度的影响分布图。从图中可以看出，当拓扑荷数l增大时，能量密度和动量密度中心环的半径增大，即逐渐向外扩展，且峰值的位置发生较大改变。随着拓扑荷数l的增大，自旋角动量密度的分布由环形分布转变为两瓣的月牙形分布，轨道角动量密度的圆环半径逐渐增大，且峰值位置发生较大改变。进一步观察可以发现，能量密度和动量密度的方向均呈现出顺时针方向的旋转，不同拓扑荷数l下的自旋角动量密度与轨道角动量密度的旋转方向总是相反的。

图4给出的是费米能量对涡旋光束在石墨烯表面反射后能量、动量、自旋角动量和轨道角动量密度的影响分布图。从图中可以看出，当入射角θi<50°时，费米能量对反射光束的能量密度影响较小，当入射角θi>50°时，反射光束的能量密度呈现先增大后减小的趋势。动量密度和轨道角动量密度变化趋势相似，均随着入射角的增大而增强，从θi=60°开始迅速增大，且当θi<70°时，费米能量越小，动量密度和轨道角动量密度越小；当θi>70°时，费米能量越小，动量密度和轨道角动量密度越大。自旋角动量密度呈现先减小后增大的趋势，谷值随着费米能量的增大而增大，且费米能量越大，达到谷值的所对应的入射角也越大。达到谷值前，费米能量越小，自旋角动量密度越小，达到谷值后，费米能量越小，自旋角动量密度越大。

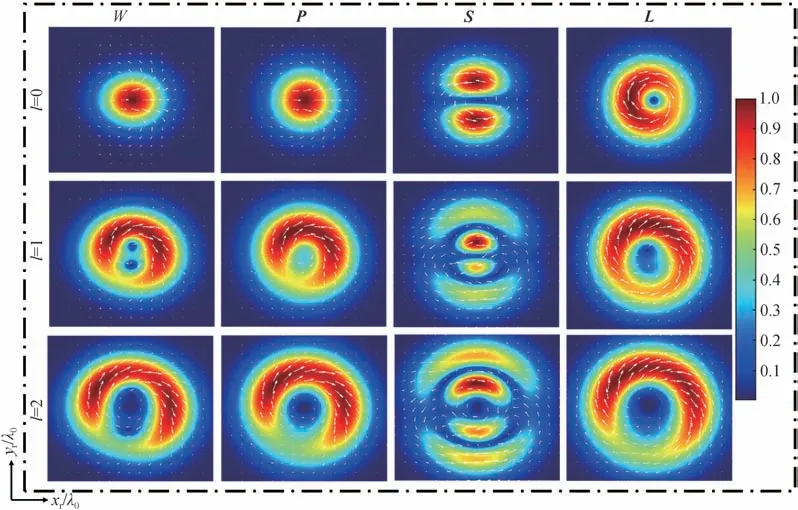
图 3 拓扑荷数对涡旋光束在石墨烯表面反射后能量、动量、自旋角动量和轨道角动量密度的影响Fig.3 Effect of the topological charge on the energy， momentum， SAM and OAM densities of the vortex beams reflected from a graphene-substrate interface

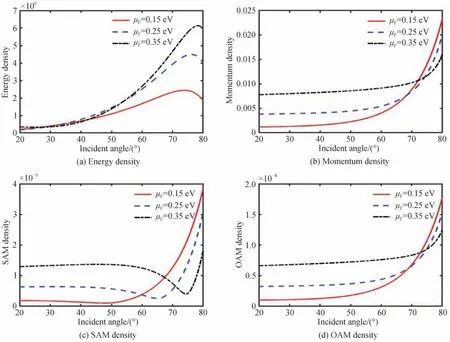
图 4 费米能量对涡旋光束在石墨烯表面反射后能量、动量、自旋角动量和轨道角动量密度的影响Fig.4 Effect of the Fermi energy on the energy， momentum， SAM and OAM densities of the vortex beams reflected from a graphene-substrate interface

图5是磁场对涡旋光束在石墨烯表面反射后能量、动量、自旋角动量和轨道角动量密度的影响分布图。从图中可以看出，当入射角θi<50°时，磁场强度对反射光束的能量密度影响较小，当入射角θi>50°时，反射光束的能量密度呈现先增大后减小的趋势，且磁场强度越小，峰值越大。动量密度和轨道角动量密度呈现相似的变化趋势，均随着入射角的增大而增强，且从θi=60°开始迅速增大，当θi>75°后，磁场强度对反射光束的动量密度和轨道角动量密度影响较小。自旋角动量密度呈现先减小后增大的趋势，谷值随着磁场强度的增强而减小，且磁场强度越强，达到谷值的所对应的入射角越小。达到谷值前，磁场强度越小，自旋角动量密度越大，达到谷值后，磁场强度越大，自旋角动量密度越大。

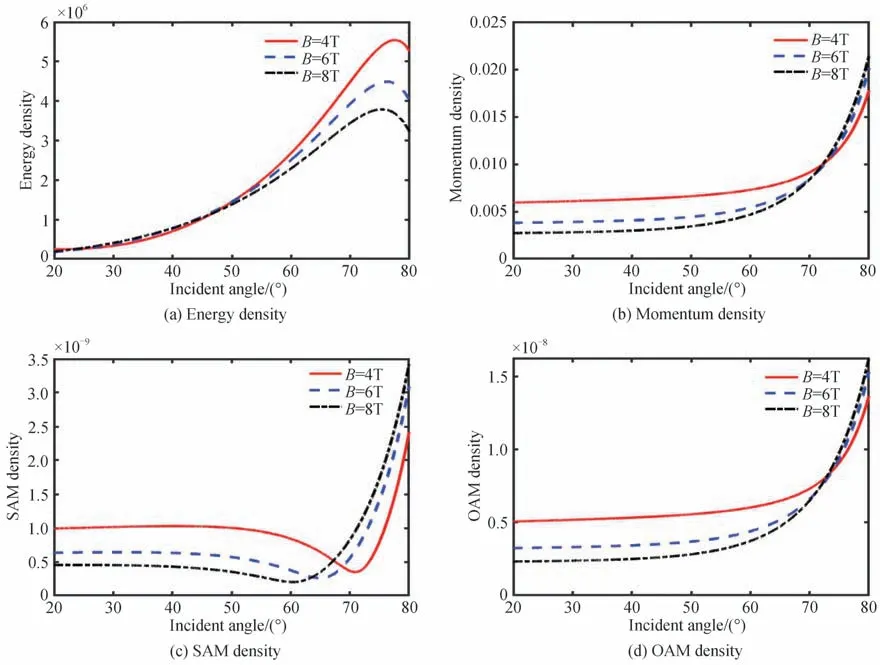
图5 磁场对涡旋光束在石墨烯表面反射后能量、动量、自旋角动量和轨道角动量密度的影响Fig.5 Effect of the magnetic field on the energy， momentum， SAM and OAM densities of the vortex beams reflected from a graphene-substrate interface

3 结论

理论分析和数值模拟研究了石墨烯表面涡旋光束的局域动力学特性。建立了LG涡旋光束从空气入射到石墨烯-衬底系统表面反射的全矢量理论模型，推导出了LG涡旋光束在石墨烯表面反射后电场和磁场分量的解析表达式。通过数值模拟，分析了光束参数和石墨烯材料参数对反射涡旋光束局域动力学特性的影响。数值结果表明，石墨烯表面反射涡旋光束的能量、动量、自旋/轨道角动量密度分布在布儒斯特角附近发生突变。光束拓扑荷数的增大使能量、动量和自旋/轨道角动量密度的分布向外扩展，峰值位置发生较大改变。当入射角较小时，费米能量和磁场对反射涡旋光束的能量密度影响较小；当入射角度较大时，费米能量越大或磁场越小，能量密度越大。动量和轨道角动量密度随费米能量和磁场的变化呈现相似的变化趋势，当θi<70°时，费米能量越小或磁场越大，动量和轨道角动量密度越小。自旋角动量密度随费米能量和磁场的变化随着入射角的增大呈现先减小后增大的趋势，费米能量越大或磁场越小，达到谷值的所对应的入射角越大。本文建立的理论模型和推导得到的电磁场分量表达式可用于计算石墨烯表面涡旋光束的螺旋度和手性，研究基于石墨烯对涡旋光束螺旋度和局域手性的调控，为新型光电子器件的设计等技术提供理论基础与技术支撑。