函数插值分析研究与应用

郭佳欣

（北京建筑大学，北京 102616）

实际问题中经常有这样的函数y=f(x)，其在某个区间[a，b]上有有限个离散点x0,x1,…xn，且这些点对应函数值为yi=f(xi)(i=0,1,2...)，若想得到其它点的值就必须找一个满足上述条件的函数表达式。

1 Lagrange 插值函数

1.求作n 次多项式pn(x)，使满足条件：

这就是所谓的拉格朗日（Lagrange）插值。点xi（它们互不相同）称为插值节点。用几何语言来表达这类差值，就是通过曲线y=f(x)上给定的n+1 个点(xi,yi)(i=0,1,...,n)，求作一条n 次代数曲线y=pn(x)作为y=f(x)的近似。

2.拉格朗日插值公式。

（1）首先考察线性插值的简单情形。若y=f(x)表示过两点(x0,y0),(x1,y1)的直线，这个问题是我们所熟悉的，它的解可表示为对称式：

此类为一次插值，称为线性插值。若令：

由此可得：l0(x0)=1,l1=(x1)=1,l1(x0)=0，则有：p1(x)=l0(x)y0+l1(x)y1，这里的l0(x),l1(x)可以看作是满足条件l0(x0)=1,l0(x1)=0l1(x1)=1,l1(x0)=0的插值多项式，这两个特殊的插值多项

式称作上述问题的插值基函数[1-2]。

（2）抛物插值。线性插值仅仅利用了两个节点的信息，精度自然很低，为了提高精度，进一步考察二次插值。若y=f(x)表示过三点(x0,y0),(x1,y1),(x2,y2)的曲线，求它的解。二次插值的几何解释是，用通过三点(x0,y0),(x1,y1),(x2,y2)的抛物线y=p2(x)来近似所考察的曲线y=f(x)，因此这类插值亦称为抛物插值。

根据上述解决方法，同理可以得出：

容易看出，这样构造的p2(x)为问题的解。

（3）推广到一般：已知函数在n+1 个不同点x0,x1,...xn上的函数值分别为y0,y1,...yn求一个次数不超过n 的多项式pn(x)，使其满足：pn(xi)=yi(i=0,1,...n)即n+1 个不同的点可以决定的一个n 次多项式。过n+1 个不同的点分别决定n+1 个n 次插值基函数。l0(x),l1(x),...ln(x)每个插值基多项式满足：a.li(x)是n 次多项式；b.li(x)=1，而在其它n 个点li(xk)=0,(k≠i)。由于li(xk)=0,(k≠i)，故有因子(x-x0)...(x-xi-1)(x-xi+1)...(x-xn)因其已经是n 次多项式，故而仅相差一个常数因子。令li(x)=a(x-x0)...(x-xi-1)(x-xi+1)...(x-xn)由li(xi)=1，可以定出a,进而得到：

则n 次拉格朗日型插值多项式pn(x)=y0l0(x)+y1l1(x)+...ynln(x)，从而pn(x)是一个次数不超过n 的多项式，且满足pn(xi)=yi(i=0,1,...n)[3-5]。

2 Newton 插值函数

2.1 Newton 法的简述

设(x-xk)是f(x)的一个近似根，把f(x)在xk处泰勒展开：

若取前两项来近似代替f(x)，则f(x)=0 的近似方程为f(x)=f(xk)+f'(x)(x-xk)=0。设f'(x)≠0，设其根为xk+1，则xk+1的计算公式为：

这即为牛顿法，其迭代函数为：

牛顿法其实是一种逐步的线性化的方法，它的本质是将f(x)=0 非线性方程的求根问题归结为类似的一系列的线性方程f(xk)+f'(x)(x-xk)=0 的根。

2.2 具有承袭性的插值公式

先考察线性插值的插值公式：

由于p0(x)=f(x0)可看作是零次插值多项式，上式表明p1(x)=p0(x)+c1(x-x0)其中，修正项的系数：

再修正p1(x)以进一步得到抛物插值公式的解p2(x),为此，令：

显然，不管系数c2 如何取值，p2(x)均能满足两个条件：p2(x0)=f(x0),p2(x1)=f(x1)，再用剩下的一个条件p2(x2)=f(x2)来确定c2，结果有：

记c0=f(x0)，从而有：p2(x)=c0+c1(x-x0)+c2(x-x0)(x-x1)

以上论述表明，为了建立具有承袭性的插值公式，需要引进差商并研究其性质。

2.3 差商及其性质

对于给定的函数f(x),记f(x0,x1,...,xn)表示关于节点x0,x1,...,xn的n 阶差商。一阶差商定义为：

二阶差商定义为一阶差商的差商：

一般地，n 阶差商递推定义为：

为统一起见，补充定义函数f(x1)为零阶差商。

一般地，用数学归纳法易证：

2.4 差商形式的插值形式

这种差商形式的插值公式称作牛顿插值公式，牛顿公式其实只是拉格朗日公式的一种变形[6-7]。

3 Hermite 插值法

1.在某些问题中，为了保证插值函数能更好与原来的函数重合，使插值函数更接近原来函数轨迹，不但要求“过点”，即两者在节点上具有相同的函数值，而且要求“相切”，即在节点上还具有相同的导数值，这类插值称作切触插值，或称埃尔米特（Hermite）插值。显然，埃尔米特插值是泰勒插值和拉格朗日插值的综合和推广。

2.Hermite 插值基本原理。通常如上条件的Hermite型插值是通过构造相应的插值基函数来完成的，为方便起见，以n=1 为例，说明传统的求解方法，设给定的x0,x1和相应的函数值f(x0),f(x1)及微商值f'(x0),f'(x1)构造插值函数H3(x)。由构造函数的办法可知：对应于x0和x1点函数值的插值函数分别为：

而对应的x0和x1点导数值的插值基函数分别为：

因此所要求的插值函数H3(x)=f(x0)h0(x)+f(x1)h1(x)+f'(x0)H0(x)+f'(x1)H1(x)。

4 插值法的应用

加工零件的轮廓曲线：该问题是有一个待加工零件，它的外形根据工艺要求由一组数据（x,y）给出（在平面情况下），要求要用数控机床加工时刀具必须沿这些数据点前进，并且由于刀具每次只能沿x 方向或y方向走非常小的一步，所以需要将已知数据加密，得到加工所要求的步长很小的（x,y）坐标。

表1 给出了轮廓线上x 每间隔0.2（长度单位）的加工坐标x,y（顺时针方向为序，由轮廓线的左右对称性，表中只给出右半部的数据），假设需要得到x 或y坐标每改变0.05 时的坐标，试完成加工所需的加密数据，画出该零件的轮廓曲线。运用matlab 绘画出的加工零件轮廓线，用不同的插值方法，画出最好的效果图。最后得出运用三次样条插值，画出的轮廓图最好。

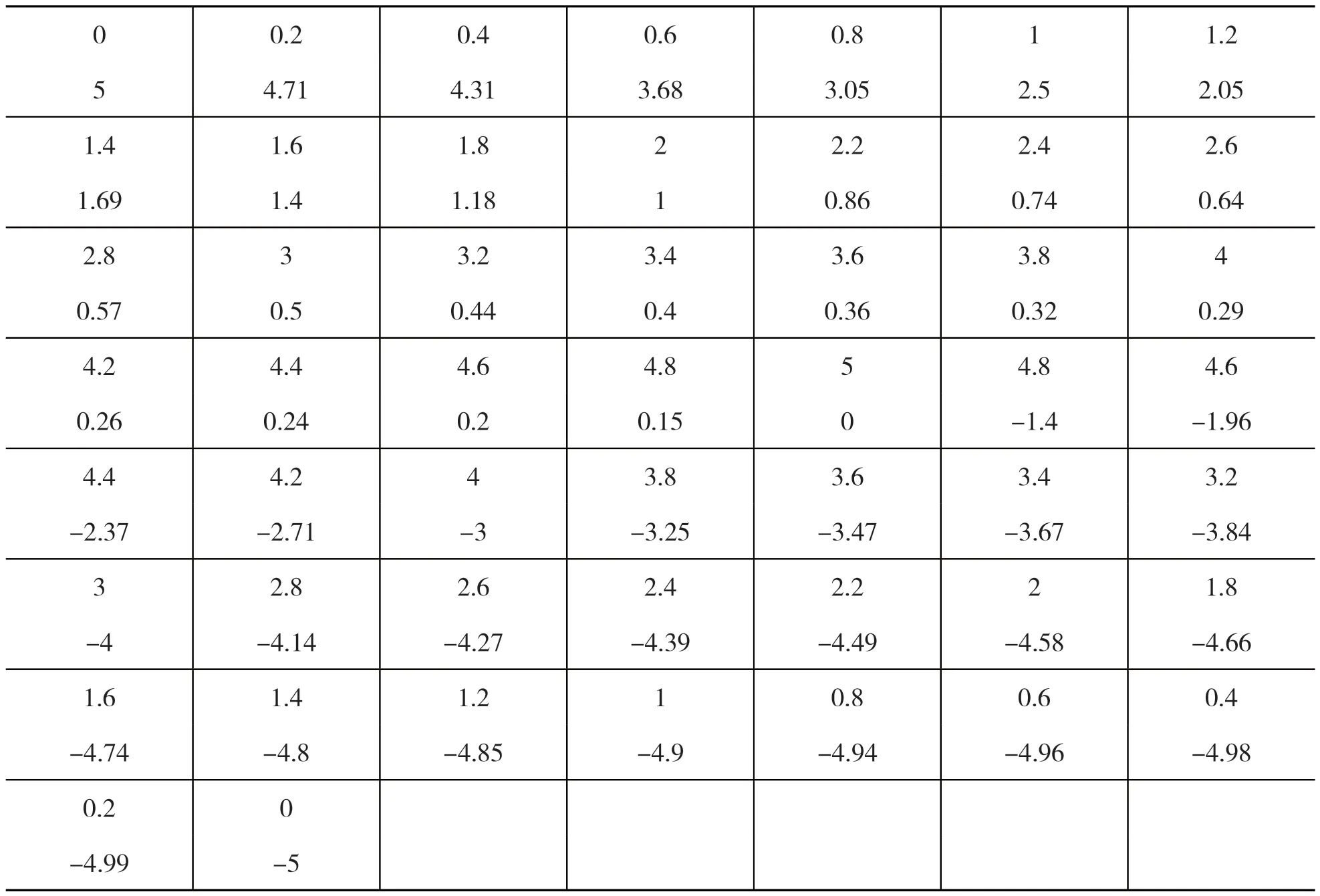
表1 x 间隔0.2 的加工坐标（x,y）（右半部的数据）

5 结语

我们通过对函数插值的分析及研究，用解决实际问题的方法，对不同的插值方法都有了深刻的了解，并掌握了运用matlab 解决插值问题，明白了各个插值方法的含义。这让我们不仅仅局限于理论知识的理解，更上升到了实际问题中，加深了我们对于插值函数的认识。