用LSTM对市级周交通事故量预测方法研究

孙振华，王转转，肖 鑫

(1.绍兴市交通建设有限公司，浙江 绍兴 321000；2.长安大学 信息工程学院，陕西 西安 710064)

0 引 言

城市交通事故量是衡量一个城市特定时间内道路安全水平的重要指标。交通事故的发生虽然微观上具有一定的不确定性和随机性，但在宏观空间层面上还呈现一定的规律性，因而具有可预测性。当前，预测的方式主要可以分为实时预测和短周期(如周和月)预测。实时预测通常应用深度学习技术结合获取的空间多源交通数据进行模型训练并进行交通事故量的预测[1-2]；短周期交通事故量预测通常将交通事故量按时间先后顺序构成序列，对序列数据进行模型训练并进行预测。短周期交通事故量预测是市一级交警部门制定交通决策和交通措施的重要参考。对于经验丰富的交警而言，即使交通事故量时间序列基本趋势表现为明显的季节周期性特征，但叠加在周期性规律中的波动也会使他们也很难对交通事故进行较为准确的估计，因而如何使预测达到可接受的准确度是需要解决的问题。短周期城市交通事故量的准确预测需要捕获交通事故量时间序列内在的时序依赖关系。常用的基于时间序列的典型模型有自回归模型、神经网络模型以及组合模型等。

时间序列自回归模型是一种能对时间序列观测值内在时序依赖关系进行线性表征的一类模型。该类模型应用前需要对时间序列样本数据的平稳性(数据的均值、方差、协方差指标是与时间无关的常数)进行校验以决定模型类型选择并对参数定阶来反映时序依赖关系。平稳的数据适合选用自回归滑动平均模型(Auto-Regressive and Moving Average Model，ARMA)，模型阶数p与q分别表示序列观测值由过去的p个序列观测值和q个随机扰动的线性组合来表示。这两个参数可通过计算相关系数和偏自相关系数并通过模型参数优化方法最终确定，并由残差序列是否为与时间序列无关的白噪声来评估其有效性。谢华为[3]用具有平稳特性的2003至2015年的全国交通事故数样本确定ARMA参数并对2011至2015年的交通事故数进行拟合。如果样本数据具有非平稳特点，则需要采用差分自回归移动平均模型(Auto-Regressive Integrated Moving Average Model，ARIMA)进行差分处理，差分次数d是该模型的一个输入参数。张杰等[4]发现1970至1997年全国交通事故十万人口死亡率时间序列样本数据具有非平稳特点，因此采用ARIMA进行差分处理并确定模型参数p、q和d，并对1993至1997年的死亡率进行预测。张艳艳等[5]采用ARIMA模型对非平稳的2011至2014年福建海域水上交通的月事故量进行差分处理并确定参数，对2015年各月水上交通事故量进行预测并评估误差。季节性差分自回归滑动平均模型(Seasonal Auto-Regressive Integrated Moving Average，SARIMA)在ARIMA基础上引入季节性因子来表征数据的周期性特征，并从趋势性、季节性变动以及随机变动三个维度对时间序列数据内在时序依赖关系进行度量。Halim等[6]观察到印度尼西亚孟加锡市2016至2019年间的交通事故量具有明显的季节性特征外，再引入了2020年新冠病毒流行期间事故量有明显下降趋势的数据，建立SARIMA预测模型对2021全年的交通事故量的变化趋势进行了预测。

基于神经网络的时间序列模型是能对时间序列观测值变化进行自学习的一类模型。有别于时间序列自回归模型参数的定阶依赖样本数据特征或先验知识，该类模型能自动捕获时间序列样本观测值内在的时序依赖关系并能进行样本外预测，实现这一点的前提往往需要样本数据量足够丰富，如果有同样时空相关的截面数据辅助则更好。安杰等[7]为了预测2011年交通事故中的事故数、死亡人数、受伤人数及综合死亡率，选取1997到2010年时间序列相关数据的同时，还引入了同时期的国内生产总值(GDP)、人口数、公路里程等维度数据，评估它们与同年全国交通事故量的相关性进而形成截面数据，将当年截面数据作为输入以及将来年的年交通事故量作为期望输出值，训练得到基于误差反向传播(Back Propagation，BP)神经网络的道路交通安全预测模型。李兴兵[8]等用BP神经网络对城市2011 至2016 年的每日数据作为时间序列训练样本，结合机动车年保有量、日天气因素、节假日类型等构成截面数据，并对2017年每日数据作为验证样本进行预测。由于BP神经网络模型有收敛速度慢、训练时间长、容易陷入局部极小点等缺点，因而张志豪等[9]针对1998至2012年全国交通事故死亡人数时序数据以及GDP、国民总收入、人均GDP等维度的截面数据，采用长短时记忆神经网络模型(Long Short-Term Memory，LSTM)进行模型参数的训练，并对2013至2016年全国交通死亡人数进行预测，取得了较好的预测效果。

组合模型是将多个类型模型融合起来对交通事故进行预测的一类模型，与时间序列自回归模型一样都具有很强的数据特性决定模型选择的特征。孙秩轩等[10]发现城市2006年1月至2013年6月道路交通事故月度受伤人数为非平稳数据，提出基于ARIMA模型和支持向量回归机(Support Vector Regression,SVR)的组合预测模型。该模型确定ARIMA参数来拟合2006至2012年的84个数据。由于残差波动具有明显的季节性特征，继而构造含有残差模糊粒子的子序列对SVR进行参数寻优回归拟合。这样得到的组合模型的预测准确度相比于单一ARIMA模型有明显提高。谢学斌[11]基于ARIMA 和XGBoost (Extreme Gradient Boosting，极端梯度提升)组合模型对1951至2010年全国交通事故量进行拟合。XGBoost是一种基于决策树的分布式高效梯度提升算法，在该研究中实现对ARIMA模型拟合值残差进行预测。张志豪等[12]提出LSTM-GBRT(Gradient Boosted Regression Trees, 梯度提升回归树，是一种基于决策树的分布式高效梯度提升算法)组合预测模型，针对1998年至2012年全国交通事故中的死亡人数以及包含GDP、国民总收入、人均GDP等维度的截面数据，采用LSTM进行模型参数的训练，用GBRT实现对LSTM拟合值残差进行预测，从而提升了2013至2016年全国交通死亡人数预测的准确度。王臻[13]和张兴强提出了ARIMA和模糊神经网络模型(Fuzzy Neural Network，FNN)组合模型，用ARIMA来拟合1980至2004年全国道路交通事故量，用模糊神经网络模型(Fuzzy Neural Network，FNN)以当年的截面数据(公路里程、机动车拥有量、客运周转量、货运周转量以及GDP、事故起数)为输入，对来年的事故数作为输出量进行监督拟合学习，再通过最优加权方法确定两个模型的权重形成组合模型，利用该组合模型对全国2005至2007年道路交通事故量进行预测并取得了较好的效果。

研究工作选用LSTM对国内某市周交通事故量进行预测的原因是：

(1)对交通事故量进行预测需要捕获特定时空交通事故量时间序列内在的依赖关系，并假定依赖关系保持不变从而能进行预测。然而这种依赖关系会因交通环境、道路、车辆数量、交通参与者随着时间的变化而演变，因而采用LSTM进行参数的自学习调整对模型随时间演化就显得很有必要；

(2)当前对交通事故量预测研究所用的数据多为全国级别并以年为单位，尚没有诸如对市级周交通事故量时空下不使用截面数据的相关预测研究，这种短周期城市级的预测对交警的实际决策工作更有意义。

1 长短时记忆神经网络模型

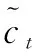
it=δ(Wi·[at-1,xt]+bi)

(1)

ot=δ(Wo·[at-1,xt]+bo)

(2)

ft=δ(Wf·[at-1,xt]+bf)

(3)

(4)

(5)

ht=at=ot*tanh(ct)

(6)

其中，δ和tanh分别代表激活函数Sigmoid和双曲线正切函数这两类非线性函数，W和b表示相应的权重系数矩阵和偏置向量，“*”表示点乘。LSTM根据输入序列计算输出序列并与设定的期望值进行误差分析，通过迭代更新系数的学习方式使误差最小化或收敛，从而具有逼近可表征观测值函数的能力，即捕获当前序列观测值和前序观测值的时序依赖关系，最终完成系数调整的LSTM神经网络就具有了对训练样本的拟合以及对验证样本的预测能力。正因为如此，LSTM神经网络及其扩展型已应用到具有时间序列特征但时序观测值关系复杂的交通预测当中，除交通事故量预测外，还应用于短时交通流预测[14-15]、异常驾驶行为检测[16]、道路交通速度预测[17]、铁路货运量预测[18]、交通流状态预测[19]、船舶航迹预测[20]、公交行程时间预测[21]等。

图1 LSTM模型逻辑结构

2 用LSTM对市级周交通事故量预测方法

2.1 数据预处理

(1)构造日粒度交通事故量时间序列。

对一个城市特定的时间段内按照每日发生的事故起数进行统计，就可构造出日粒度交通事故量时间序列Seq_X1={x1,x2,…,xt}。

(2)时间序列观测值的离差标准化。

由于序列中的交通事故观测值波动较大，这会影响到LSTM训练的速度和精度。为消除这种影响，需针对观测值序列进行如式(7)的离差标准化[22]处理。

(7)

经过离差标准化处理后的时间序列表示为：

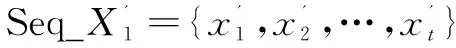
2.2 构建对应最优滑动窗口的LSTM市级日交通事故量预测模型

(1)构造训练集。

训练集X1与Y1如式(8)所示：

(8)

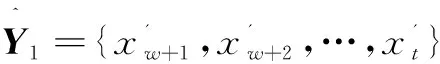
(2)确定LSTM超参数。

LSTM隐含层存储单元个数N：

隐含层数目设为1，其存储单元个数按经验公式(9)来确定。

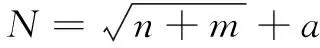
(9)

其中，n=w,m=1 ，a可取1到10中的一个值，此处a取10。

损失函数：

损失函数选用平均绝对误差(MAE)，表示训练集拟合结果与期望输出值的偏离程度loss，如式(10)所示。

(10)

迭代次数epochs：

该参数表示用(X1,Y1)训练LSTM并使式(10)的误差loss趋向收敛的次数，可通过观察来确定。

(3)确定最优滑动时间窗口算法。

滑动窗口w决定了(X1,Y1)构成，不同的(X1,Y1)训练出的LSTM预测模型的拟合结果误差有所不同，即w间接决定了误差值，因而需要确定一个最优长度的w'，从而使训练出的LSTM预测模型拟合误差最小，相应的算法如图2所示。

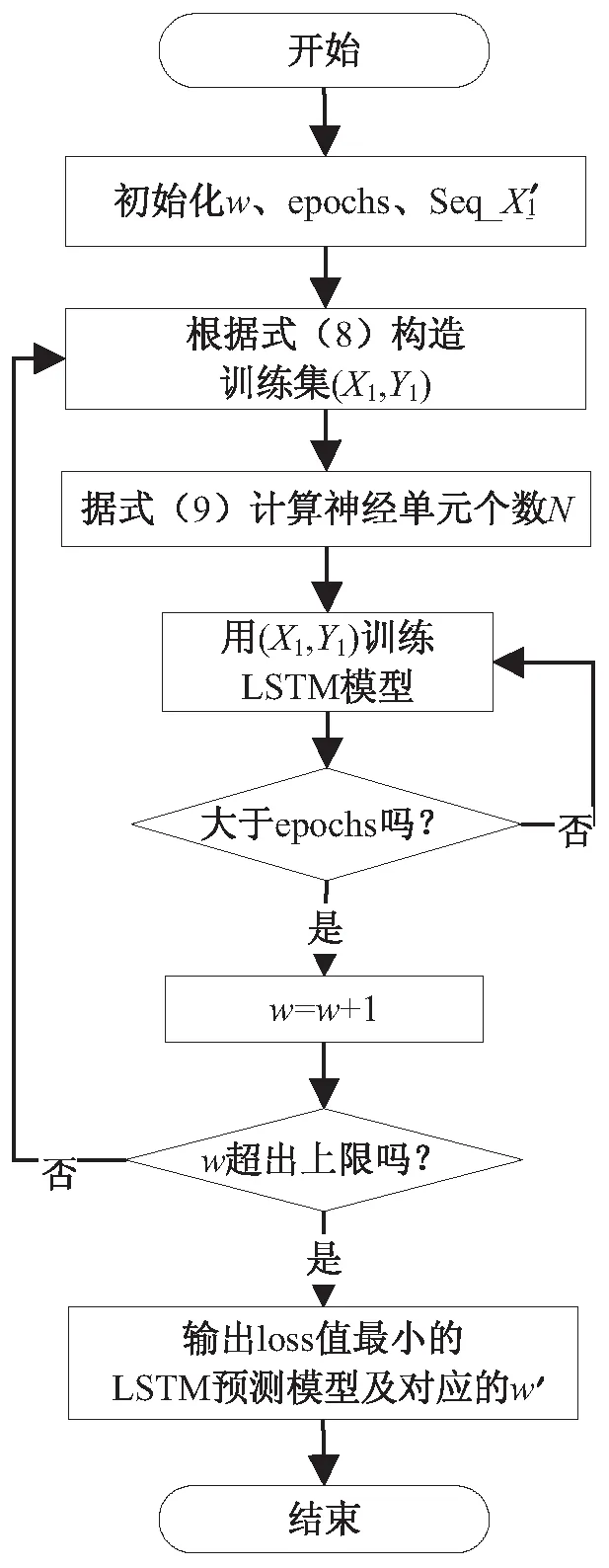
图2 最优滑动窗口算法流程

2.3 评估对应最优滑动窗口LSTM市级日交通事故量预测模型预测结果对验证集的周粒度拟合效果

(1)构造验证集。

(11)

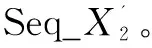
(2)预测结果对验证集的周粒度误差评估。

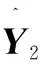
(12)

(3)预测结果对验证集的周粒度拟合效果评估。

(13)

3 实验结果验证

城市交通事故发生后，执勤交警会记录每个事故人、车、路、环境的详细信息形成一条交通事故记录，包括事故发生的时间、发生路段地点、车辆、驾驶员、环境、财产损失、伤亡人数、雨雪天气等。对来自国内某市2011至2015年20 988条交通事故记录按日统计就形成日粒度交通事故量时间序列1 824条。以2014年为界形成训练集和验证集，将这些日统计记录以月为单位分成四组，前三组七天为一个单位，后一组为剩余天数，统计形成周粒度交通事故量时间序列240条(以下周粒度默认指此类型)，将2011年至2014年的时间序列(其中日粒度为1 459条，周粒度为192条)作为训练集，2015年的时间序列作为验证集(其中日粒度365条，周粒度48条)。经过验证交通事故量是平稳数据，因而也可采用ARMA和SARMA进行预测对比实验。

在Keras框架中，用Python3.8对周粒度时间序列训练集按图2算法流程计算得到最优滑动窗口w'=45的LSTM市级周粒度交通事故量预测模型，其对训练集的拟合结果和验证集的预测拟合结果能很好表达数据的基本趋势，但不能很好地匹配波动的数据，因而图3中度量拟合效果和预测拟合效果的R-square指标值都欠佳。采用ARMA模型和SARMA模型也出现类似效果，这说明基于交通事故量训练的用于捕获观测值时序依赖关系的模型对数据基本趋势准确性的表达远好于对其波动性的表达。

图3 最优滑动窗口LSTM市级周级组粒度交通事故量预测模型对训练集拟合效果以及对验证集预测的拟合效果

图4展示了最优滑动窗口w'=72的LSTM市级日交通事故量预测模型对训练集的拟合结果和对验证集的预测结果与图3类似，因而度量拟合效果和预测拟合效果的R-square指标值也都欠佳。需要注意的是，细粒度下的预测结果对交通事故量基本趋势的准确描述可转化为粗粒度下对波动性准确描述的事实，如周粒度下显著的波动在日粒度下则表现为较为平缓的变化趋势叠加小规模的波动。将这三类模型的拟合结果和预测结果从日粒度转为周粒度统计口径后，如图5所示，三个模型相对于图3各自都提升了拟合效果和预测拟合效果，尤其是LSTM和ARMA模型较为明显，度量预测拟合效果的R-square指标值分别为0.817和0.832，这意味着预测结果整体上与实际结果吻合程度分别达到了81.7%和83.2%。而SARIMA模型拟合效果相对较差的原因可解释为数据季节周期性相对不突出所致。需要明确的是，LSTM预测模型对验证集较为准确的预测能力实际上是来自对训练集交通事故量时间序列内在依赖关系的学习与量化(ARMA也是如此)，然而图5中描述验证集的预测拟合效果的R-square指标值0.817稍高于训练集拟合效果0.719，这可解释为正常的交通事故量波动引起。对于市级周交通事故量预测而言，平均绝对百分比误差在15%以内是可接受的准确度，图5中LSTM和ARMA模型对训练集的拟合结果和对验证集的预测结果的平均绝对百分比误差都在这一范围内。

图4 最优滑动窗口LSTM市级日交通事故量预测模型对训练集拟合效果以及对验证集预测的拟合效果

图5 最优滑动窗口LSTM市级日交通事故量预测模型的输出结果转为周粒度时对训练集拟合效果以及对验证集的预测拟合效果

图6展示了2011～2014年期间七天为一周的统计口径得到的周交通事故量以及划分的训练集和验证集，与图5对比可发现，虽然交通事故量曲线有了明显变化，但是LSTM和ARMA则保持了同样好的拟合效果和预测拟合效果，从另一个侧面也印证了细粒度下预测结果对交通事故量基本趋势的准确描述可转化为粗粒度下对波动性的准确描述。虽然LSTM和ARMA都取得了较好的预测效果，但LSTM不像ARMA那样需要人工辅助来进行参数定阶，这个优点有利于LSTM随时间而滚动更新参数以保证预测的准确性，毕竟市级周交通事故时间序列内在依赖关系会随时间有所变化。然而需要注意的是，滑动时间窗口的长度对基本趋势准确描述有直接影响。图7展示了滑动窗口w=306的LSTM市级日交通事故量预测模型输出结果转为周粒度后对训练集的拟合和对验证集的预测拟合效果，两个R-square指标值的显著下降可解释为w=306滑动窗口首先会造成日粒度下对验证集的基本趋势描述准确度下降，进而影响了周粒度下对数据波动描述的准确度。图8展示了滑动窗口长度w与周粒度拟合效果和预测拟合效果的R-square指标值的关系——呈现了先增大后减小趋势，这个变化过程说明采用最优窗口算法为LSTM市级日交通事故量预测模型确定最优窗口长度很有必要。

图6 最优滑动窗口LSTM市级日交通事故量预测模型的输出结果转为七天一周统计口径时对训练集拟合效果以及对验证集的预测拟合效果

图7 w=306滑动窗口LSTM市级日交通事故量预测模型输出结果转为周粒度时对训练集拟合效果以及对验证集预测的拟合效果

图8 LSTM市级日交通事故量预测模型输出结果转为周粒度时对训练集拟合以及对验证集预测的R-square值与滑动窗口长度关系

实验结果表明，提出的“用LSTM对市级周交通事故预测方法”可基于市级日粒度交通事故量时间序列对周交通事故量进行较为准确的预测。对交通事故量进行预测目前类似研究所用的数据多为全国每年的交通事故量时间序列，但由于该类数据量较少而很难发挥神经网络模型自我学习能力来捕获数据的时序依赖关系，往往需要补充多维截面数据，但截面数据会因涉及多个行业部门以及在统计上的滞后会影响交通事故量预测的时效性，而只基于交通事故量时间序列进行预测则会减少这方面的困难并增强预测模型的实用性。

4 结束语

(1)提出了用LSTM对市级周交通事故量预测方法。该方法通过构建一个对应最优输入序列长度的LSTM市级日交通事故量预测模型捕获交通事故量时间序列中的当前观测值与前序观测值的时序依赖关系，当将预测结果转为周粒度统计口径后，就实现了对交通事故量较为准确的预测。该方法不需要相关截面数据，因而对市级交警预测交通事故量具有实用价值。

(2)市级交通事故量时间序列的波动是影响对其准确预测的关键因素，所提的预测方法解决了影响市级周交通事故量准确预测的问题。该方法发现基于交通事故量训练的用于捕获观测值时序依赖关系的LSTM模型对数据基本趋势准确性的表达远好于对数据波动性的表达，为此提出最优窗口算法来确定LSTM模型最优窗口长度，以确保对训练集基本趋势表达的准确性，再根据所发现的预测结果对细粒度交通事故量基本趋势的准确描述可转化为粗粒度下对波动性准确描述的事实，将日粒度预测结果转为周粒度后就取得了较准确的预测效果。

(3)用LSTM对市级周交通事故量预测方法能进行较为准确预测的前提是验证集和训练集保持相同的时序依赖关系。随着时间的推进，如果预测结果与训练集时间过久很难保证这种时序依赖关系不发生变化，因而下一步将研究市级日交通事故量LSTM预测模型的自我优化更新机制来保持预测的准确性。