一种基于模板的二阶段ZS细化算法

陈 品，王 涛，张德港

(华南师范大学 计算机学院，广东 广州 510631)

0 引 言

细化算法是指在保持原二值图像的拓扑结构和连通性的前提下，生成单像素宽度的骨架图[1]。骨架是一种重要的图像几何特征，利用骨架来表示原始图像，可以在保持图像重要拓扑信息的前提下极大地消除图像中的冗余信息,提取目标特征,简化后续图像处理数据量,提高运行速度。因此，细化是很多图像预处理中的重要步骤,目前细化算法已经广泛应用于指纹识别[2]、汉字处理[3]、裂缝检测[4]、仪表检测[5]、物料分选[6]等场景。

优秀的细化算法应在维持原图拓扑结构的前提下,既保持骨架的连通性，又不会过度腐蚀,并具有一定的抗噪性能。理想的细化纹线骨架应在中间位置,且保持纹线的连接性、拓扑结构和细节特征。因此，细化算法应满足以下几点要求[7]：

(1)收敛性：迭代必须是收敛的。

(2)连接性：不破坏纹线的连接性。

(3)拓扑性：不引起纹线的逐步吞食,保持原图像的基本结构特性。

(4)保持性：保护原图像的细节特征。

(5)细化性：骨架纹线的宽度为1个像素,即单像素宽。

(6)中轴性：骨架尽可能接近条纹中心线。

(7)快速性：算法简单,速度快。

由以上7点要求中可以发现,前6条要求主要集中在对细化质量的评价,最后一条是对细化速度的要求。因此，评价一个细化算法的优劣,主要是从细化质量和细化速度两个方面进行。

根据细化算法实现特点,可将细化算法分为两大类：迭代法和非迭代法。非迭代细化算法不以基本像素点为处理条件,而是通过直接计算图像的中心线或中值线生成骨架图。非迭代算法的最大优点是处理速度快,但缺点是骨架有时会断开或留下一些不必要的分支,通常骨架连通性差。迭代细化算法在每次迭代中以相同的条件迭代删除边缘像素点,直到生成骨架。迭代细化算法可分为串行细化算法和并行细化算法。串行细化算法通过光栅扫描或跟踪图像轮廓,按顺序标记删除边缘像素点,删除条件取决于之前所有迭代的结果和本次迭代中已处理过像素点情况。串行细化算法在处理目标图像时,采用边检验边删除的方式,虽然运行速度快,但每次像素点判定是否删除难以预测,同时受到扫描顺序的影响,容易造成骨架不对称。并行细化算法在每次迭代用相同的约束条件处理目标图像中所有的像素点,检测并标记符合条件的像素点,在完成扫描后统一删除。并行细化算法每次迭代细化的结果仅与本次目标像素点的邻域相关,像素点的保留与否确定,骨架对称性较好,因此并行细化算法成为研究的热点。

ZS细化算法[8]是经典的快速并行细化算法之一,该算法能较精确地保持直线、T型交叉点和拐角等结构,细化速度快。但该算法会存在二像素斜线结构斜线细化消失的现象,同时细化后也会产生二像素宽度的冗余像素,此外2×2像素正方形结构在细化后消失。ZS细化算法在细化过程中交替消去左上边缘像素和右下边缘像素,消去操作不匀称,容易产生边缘轮廓分叉现象。LW细化算法[9]在ZS细化算法基础上进行改进,放宽了迭代过程中像素删除的判定条件,使得二像素斜线结构保留,避免二像素斜线结构局部信息丢失,但会产生更多边缘轮廓分叉,也没有解决冗余像素的问题。牟少敏等人[10]通过制作像素8邻域的十进制模板,增加特定模板删除条件，该算法解决了ZS 细化算法的像素冗余问题,改善了局部信息丢失问题,但该算法在X形状的结构保持上效果并不好。韩建峰等人[11]通过完善ZS细化算法的判决条件来改进二像素宽度斜线信息腐蚀过度问题,但其细化结果仍存在局部信息丢失问题。包建军等人提出的EPTA细化算法[12]在ZS细化算法基础上新增一个迭代结束条件来保留只有连接数为2的待删除的像素点集合,并新增一个阶段利用两个条件删除冗余像素,但该算法依然存在斜线细化畸变以及冗余消除不完全的问题。针对单幅斜线图像细化，存在其他轮廓点且所需要的迭代次数高于纯粹的二像素斜线时,判决条件将会失效,造成斜线细化畸变。赵丹丹等人提出的IEPTA细化算法[13]在EPTA细化算法的基础上新增两个对称的映像迭代过程,并同时增加了对连接数为2的删除模板,在二阶段扫描中增加两个删除冗余像素的条件,从而彻底去除冗余像素。但该算法存在2×2像素正方形结构的消失与边缘轮廓分叉的问题。MZS细化算法[14]利用像素奇偶性进行细化,但像素的坐标索引值的奇偶性会对细化结果有直接影响。袁良友等人[15]提出一种引入平滑迭代的骨架提取细化算法IZS,在ZS细化算法的基础上增加4×4保留模板与删除模板,但参数平滑参数k设置会直接影响到细化质量。OPTA细化算法也是经典的并行细化算法之一,该算法每次进行单步迭代,使用8个消除模板和2个保留模板进行骨架细化。该算法的保留模板为偶数大小模板,删除模板中凸角结构比凹角结构细化速度更快,操作不均匀,导致骨架中轴性差、像素冗余和骨架畸变。NFPT细化算法[16]将ZS细化算法与OPTA细化算法相结合,提高了细化速率,但该算法对图像T型交叉点结构效果不佳。

由以上分析可见,现有对ZS细化算法的改进算法各有优缺点,受到IZS细化算法与NFPT细化算法的启发,该文在ZS细化算法的基础上提出一种基于模板的二阶段改进算法。实验表明，提出的改进算法在保留ZS细化算法的优点同时,解决了二像素细化的问题,减少了轮廓分叉,提高了算法的鲁棒性。

1 相关工作

1.1 基本定义

设G为二值图像,前景点为白色像素并且值为1,背景点为黑色像素并且值为0。P1为图像G中任意一个值为1的目标像素点。

定义1 8邻域与16环域：与目标像素点P1相邻的8个邻域所组成的像素点集合S={P2,P3,P4,P5,P6,P7,P8,P9}称为P1的8邻域。与像素点P1相邻的16个邻域所组成的像素点集合S'={A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12,A13,A14,A15,A16}称为P1的16环域,如图1所示。

定义2 交叉数A(P1)：沿着目标像素点P1的8邻域顺时针环绕一周像素由1变为0的次数,其中P10=P2。

(1)

(2)

定义3 连接数B(P1)：沿着目标像素点P1的8邻域中像素点为1的总数。

(3)

定义4 边界点：目标像素点P1为前景点,其8邻域中至少存在一个背景点。

图1 目标像素点的8邻域与16环域

定义5 端点：目标像素点P1为前景点,其8邻域中只存在一个前景点并且为骨架点。

1.2 ZS细化算法

ZS细化算法采用8邻域方法,基于两步迭代将二值图像从左上边缘、右下边缘不断逐层消去不属于骨架的边缘像素,直到生成骨架图。ZS细化算法每次迭代可分为两个子过程：子过程1扫描并标记满足下面判定条件1、2、3、4的边界点,扫描后统一删除；子过程2扫描并标记满足判定条件1、2、5、6的边界点,扫描后统一删除。

(1)A(P1)=1

(2)2≤B(P1)≤6

(3)P2×P4×P6=0

(4)P4×P6×P8=0

(5)P2×P4×P8=0

(6)P2×P6×P8=0

ZS细化算法的迭代次数N的奇偶性决定执行不同的迭代过程,奇数迭代执行子过程1,偶次迭代执行子过程2。重复迭代上述两个子过程,直至没有像素点删除,此时剩下的点所构成的区域即为骨架,算法的细化过程结束。ZS细化算法中判定条件1要求目标像素点P1的交叉数为1,使其8邻域内像素按黑白分别聚集,防止出现交错的现象,使得目标像素点P1删除后仍然保持骨架连通性。判定条件2要求目标像素点P1的连接数在2到6之间。端点的连接数为1,不能被标记删除。若目标像素点P1连接数为7,为保证骨架的连通性,不能被标记删除,避免骨架逐步被腐蚀。判定条件3、4分别控制标记删除右下方与左上方非骨架的像素点,判定条件5、6分别控制标记删除左下方与右上方非骨架的像素点。

2 改进算法

2.1 算法思想

ZS细化算法通过迭代的方式循环删除图像中的非骨架像素点提取骨架,具有迭代少、速度快,对直线、T型交叉点和拐角细化精确等特点。但ZS细化算法在进行像素点删除判定时,仅使用目标像素点附近8邻域的信息,存在骨架毛刺,骨架斜线区域易出现像素冗余,二像素斜线结构和2×2正方形结构信息丢失等问题。细化的过程中结构信息的丢失会导致后续可提取特征点的减少,而冗余信息则会影响特征点提取的结果,特别是微小结构的丢失严重影响在某些微型结构场景下的细化效果。因此，该文提出的改进算法在细化迭代过程对于非骨架的边缘像素删除的判定中,加入目标像素点附近16环域的信息,增加5×5的模板进行细化,从而提高算法细化质量。

提出的改进算法可分为两个阶段,第一阶段生成保留部分二像素结构的骨架图,第二阶段除去冗余像素,生成单像素宽度骨架图。在第一阶段中,使用ZS细化算法的判定条件进行标记,并在迭代过程中对标记的待删除像素点中,对符合一阶段保留模板的像素点去除标记,如图2所示。其中a1-a8模板用于保留八个方向的二像素斜线结构信息,a9模板用于避免2×2正方形结构被彻底细化。同时在每轮迭代扫描中,对不符合ZS细化算法细化条件的像素点中,增加对满足交叉数为2的像素点使用一阶段额外删除模板进行标记,如图3所示。在每轮迭代扫描结束后,对标记像素点进行删除,直至没有像素点删除。第二阶段使用图4中删除模板进行2次迭代扫描,第1轮二阶段迭代扫描使用c1、c2删除模板,第2轮则使用c3、c4删除模板,对第一阶段处理后存在的二像素斜线冗余像素进行标记删除,生成单像素宽度的骨架图。

图2 一阶段保留模板

图2～图4为改进算法所使用的模板,模板中0表示在目标像素点P1的邻域或环域中像素点的值为0且为黑色背景点,1表示该像素点值为1且是白色前景点,x表示该像素点即可为1也可为0。模板中符号E1、E2、G1和G2被定义为特殊标记符号,相同特殊标记符号的像素点的值相等。标记为E1的像素点的值与E2像素点的值无关,标记为G1的像素点的值与G2的像素点的值之和大于等于1。

图3 一阶段额外删除模板

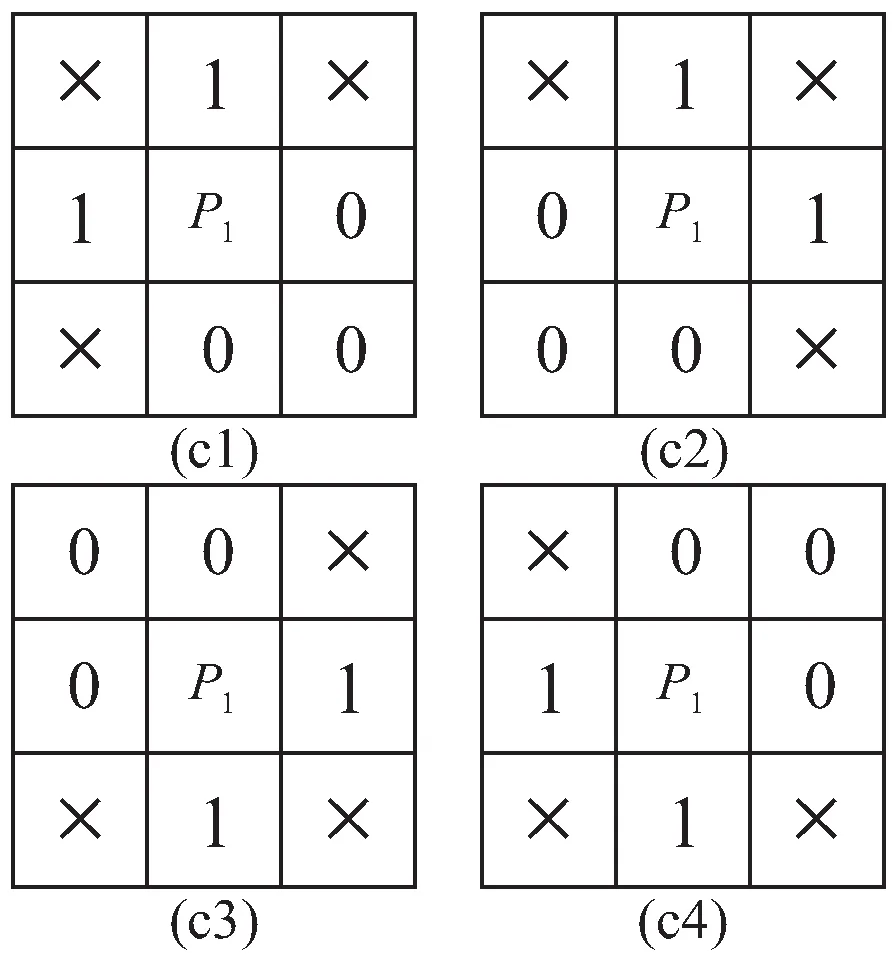
图4 二阶段删除模板

2.2 改进算法流程

改进算法主要分为7个步骤,流程如图5所示。

步骤1 初始化：迭代次数N=0。

步骤2 若迭代次数为偶数,跳转至步骤3,否则跳转步骤4。

步骤3 扫描目标图像,若像素点P1满足条件1、2、3、4且不满足一阶段保留模板a1-a9,则标记该像素点。若P1满足A(P1)=2同时B(P1)=4或B(P1)=5,并满足一阶段额外删除模板b1至b8,则标记该像素点。扫描完成后跳转至步骤5。

步骤4 扫描目标图像,若像素点P1满足条件1、2、5、6且不满足一阶段保留模板a1-a9,则标记该像素点。若像P1满足A(P1)=2同时B(P1)=4或B(P1)=5,并满足一阶段额外删除模板b1至b8,则标记该像素点。扫描完成后跳转至步骤5。

步骤5 若存在有删除标记的像素点集合,则删除像素,迭代次数N=N+1,跳转至步骤2。若删除标记像素点集合为空,跳转至步骤6。

步骤6 扫描目标图像,若符合删除模板c1、c2,则标记删除像素点。本次扫描后删除标记像素点,跳转至步骤7。

步骤7 扫描目标图像,若符合删除模板c3、c4,则标记删除像素点。本次扫描后删除标记像素点,算法结束。

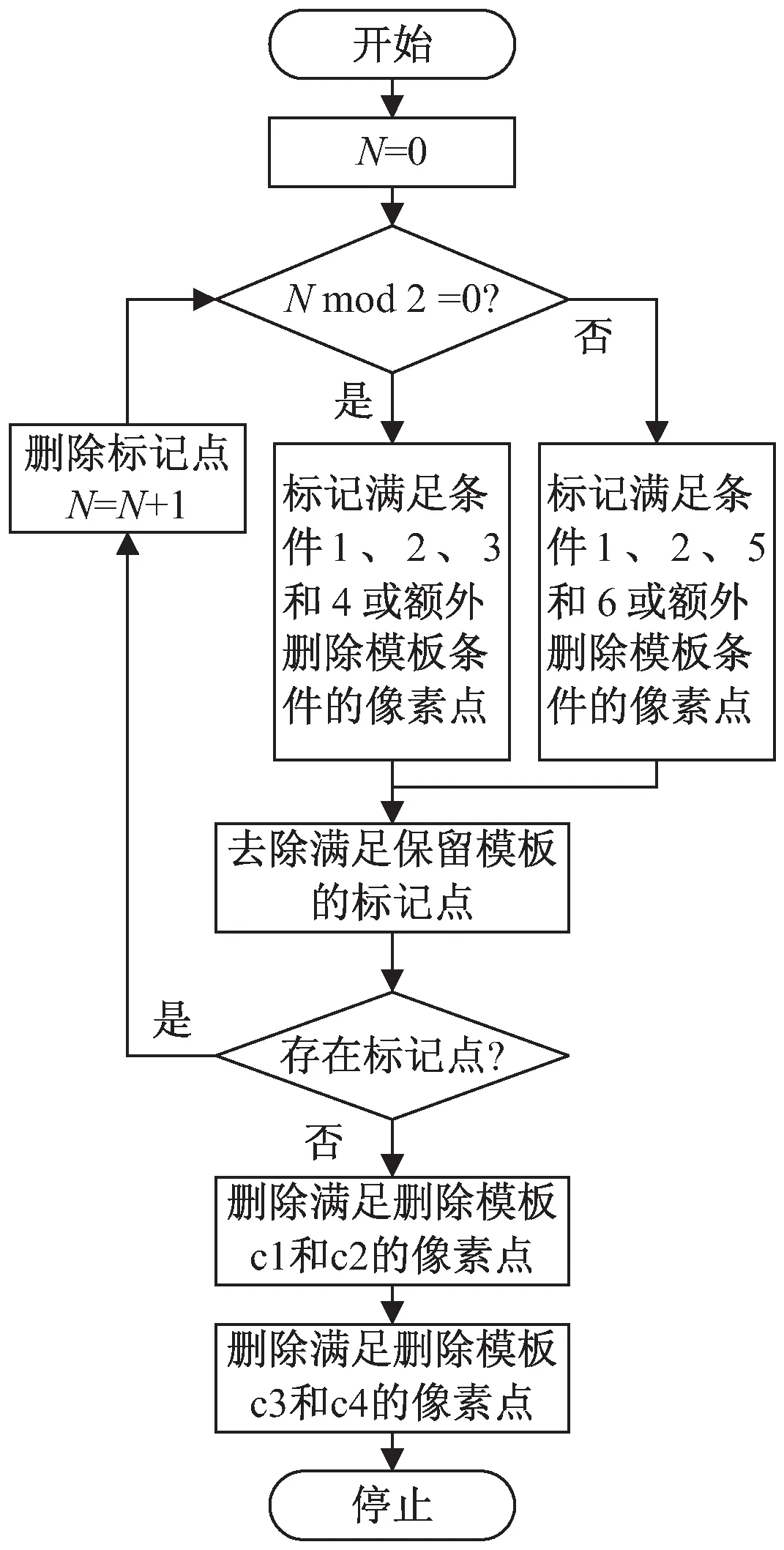
图5 改进算法流程

3 实验与分析

为了验证提出的改进算法的有效性,实验在Windows10操作系统中使用Visual Studio2019开发环境并使用OpenCV3.4.9计算机视觉库,对1 000个150×150像素常用黑体汉字进行细化,并将提出的改进算法与ZS细化算法、NFPT细化算法、IZS细化算法进行比较。图6为改进细化算法与现有细化算法对二像素宽度斜线结构、正方形结构细化后的图像对比。因细微结构对平滑迭代的敏感度高,故IZS细化算法只在汉字细化过程中加入平滑迭代进行对比。图7是分别对汉字“联”、“宾”和“资”细化后的图像对比。表1为改进算法与现有算法对汉字“联”、“宾”和“资”细化后,在各项数据上的对比结果,表2为1 000个常用黑体汉字细化后的平均结果对比。

图6 二像素斜线结构以及2×2正方形细化图

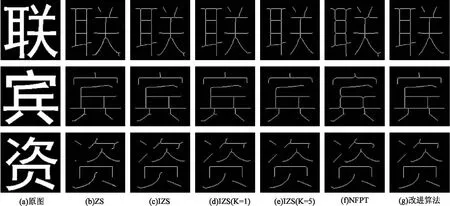
图7 汉字“联”、“宾”和“资”细化图

定义6 细化率TR[17]：图像的细化程度,由下列公式计算：

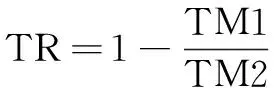
(4)

其中，TM1表示细化图像的总三角形计数,计算公式如下：

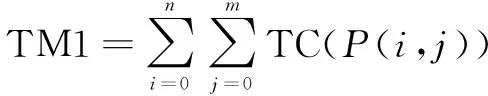
(5)

P(i,j)=1表示为二值图中前景点,TC函数用于计算P(i,j)及其相邻像素构成的白色三角形的数量,计算公式如下：

TC(p1)=p1×[(p8×p9)+(p9×p2)+

(p2×p3)+(p3×p4)]

(6)

TM2表示图像可以计算的最大白色三角形数,计算公式如下：

TM2=4×[max(m,n)-1]2

(7)

其中，m,n代表图像的矩阵P的尺寸，当TR=1时,图像将完全细化。

定义7 细化速率TS：图像平均每秒细化的像素点数,由下列公式计算：

(8)

DP=OP-SP

(9)

其中，DP为细化过程中删除的前景点数量,OP为原图中前景点的数量,SP为细化后图像中前景点的数量,ET为图像进行细化所需时间,单位为秒。

定义8 缩减率RR：图像细化过程中前景点减少率,由下列公式计算：

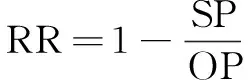
(10)

图6展示了提出的改进算法与现有算法在二像素斜线结构以及2×2正方形细化图的细化结果。ZS细化算法细化后不能完全保留二像素斜线结构信息,细化后直接生成两条短线,同时2×2正方形结构也在细化后消失。IZS细化算法、NFPT细化算法和改进算法都实现了对二像素斜线结构细化以及2×2正方形结构细化,但NFPT细化算法在二像素斜线下半部分斜线结构细化效果劣于IZS细化算法和提出的改进算法。

由图7和表1可以看出,ZS细化算法细化后存在冗余像素的问题,细化率与缩减率都最低。在“联”字右下角的笔画中细化出现了分叉毛刺,在“宾”字左下角的笔画也出现了轮廓分叉毛刺,在“资”字左上角的笔画出现了过度细化导致直接生成小点,细化时间大幅增加,细化速率最慢,而且在右上方的横钩结构细化后出现了轮廓分叉毛刺。NFPT细化算法解决了ZS细化算法存在的冗余像素问题,细化时间最短,细化速率最快。“资”字没有出现分叉毛刺问题,但“联”字与“宾”字毛刺问题依旧存在,且对T型结构交叉点处理效果不佳,细化率低于IZS细化算法和提出的改进算法。IZS细化算法没有出现二像素冗余的问题,在没有进行平滑迭代时,没有出现ZS细化算法存在过度细化的问题,但仍然存在分叉毛刺现象,缩减率和细化速率在现有改进的细化算法中最低。进行1次平滑迭代后,“联”字没有出现毛刺问题,细化率提高,但“宾”字和“资”字分叉毛刺问题仍然存在。进行5次平滑迭代后,都没有出现毛刺问题,且细化率和缩减率最高,但细化时间明显增加。该文提出的改进算法没有出现冗余像素与分叉问题,细化时间快于IZS细化算法,对T型结构处理优于NFPT细化算法,在“联”字和“资”上细化率最高,“宾”字上细化率仅次于5次平滑迭代后的IZS细化算法。

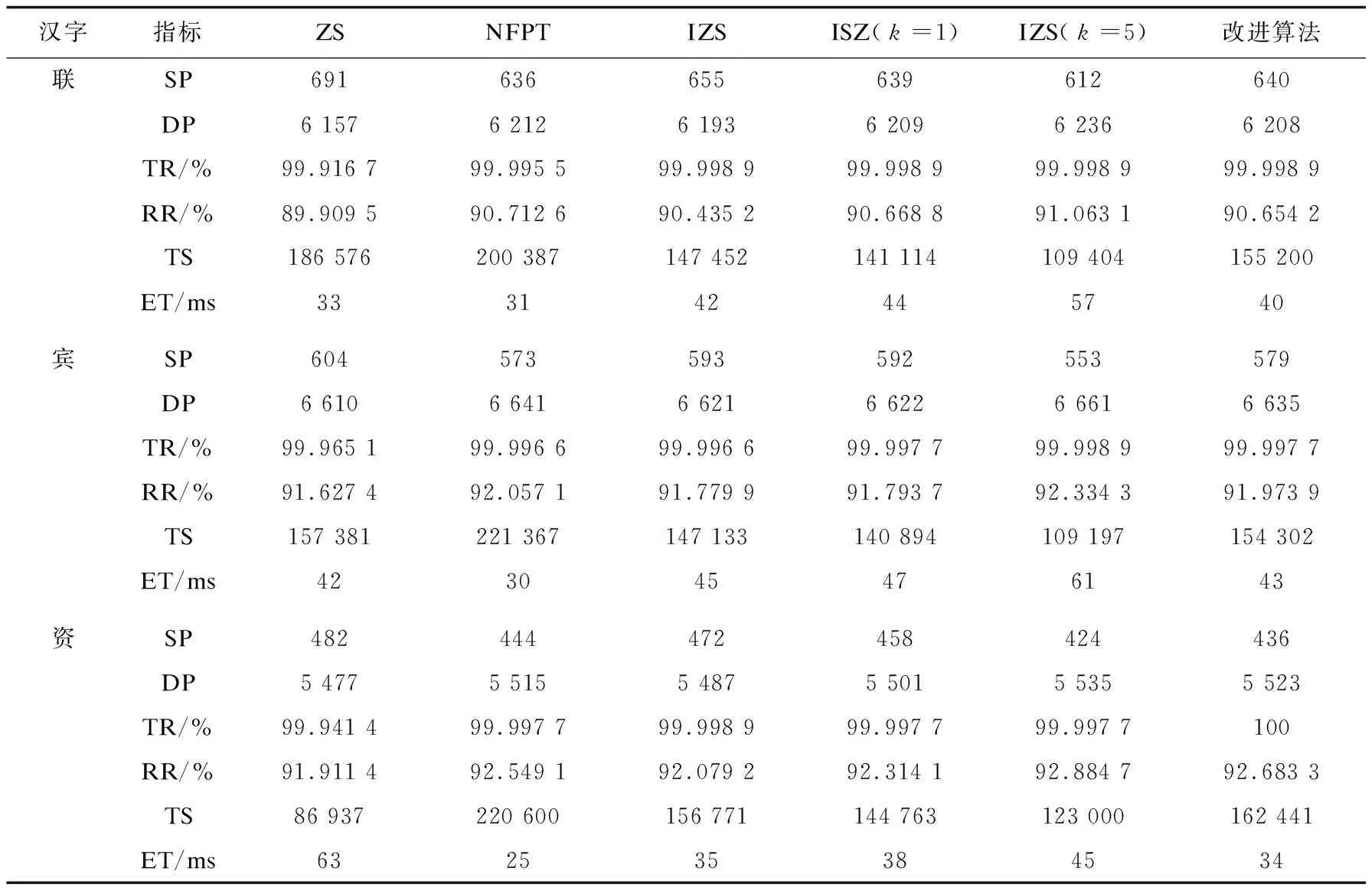
表1 汉字“联”、“宾”和“资”细化结果比较

表2展示改进细化算法和现有细化算法对1 000个常用汉字的平均细化结果,NFPT细化算法速度最快,但细化率低于IZS细化算法与改进算法,存在对T型结构交叉点细化不准确的问题。IZS细化算法细化速率最慢,通过增加平滑迭代次数可以提高细化率和缩减率。但是该算法的平滑迭代次数k需要预先设置,设置过大会导致耗时明显增大,k值设置过小则会细化不完全,平滑迭代次数的设置导致算法的实时性不稳定。该文提出的改进算法虽然增加了额外的判断条件与模板,但是细化速度仍快于未增加平滑迭代的IZS细化算法,在速度上接近ZS细化算法,而且细化率和缩减率仅次于进行平滑迭代后的IZS细化算法。

表2 1 000个常用汉字细化算法平均结果比较

4 结束语

针对ZS细化算法的缺陷,提出一种改进细化算法,该算法在ZS细化算法基础上增加5×5模板。在第一阶段针对二像素斜线结构和2×2正方形结构信息丢失等问题增加保留模板,并对交叉数为2像素点增加额外删除模板。在二阶段扫描处理中,使用删除模板对存在的二像素斜线冗余像素进行删除。实验结果表明，改进算法有效解决了ZS细化算法二像素畸变与冗余像素的问题,并且减少了细化过程中产生的轮廓分叉,完整地保留原图拓扑信息。