函数回归的差分隐私保护算法

钟可欣，杨 庚,2

(1.南京邮电大学 计算机学院，江苏 南京 210046；2.江苏省大数据安全与智能处理重点实验室，江苏 南京 210023)

0 引 言

函数型数据分析(Functional Data Analysis)是统计学中涉及对曲线、曲面或任何其他连续变化的信息分析的一个分支。对于函数型数据[1]，理想的观测单位是在某个连续域上定义的函数，观测数据由从某个总体中抽取的函数样本组成，每个函数在离散网格上采样。随着信息科学技术的发展，函数数据在诸多领域中发挥了重要作用，例如医疗行业中的扫描成像数据、社交媒体的个人行为轨迹等。

然而，函数型数据的广泛应用也存在一些急需解决的问题。隐私泄漏的危机伴随数据分析与发布等应用的出现而加深，对隐私数据的保护问题与防止敏感信息泄露的需求因此而产生。

根据响应或协变量是函数还是标量，函数回归模型可以分为四种类型[2]：(1)带有函数协变量的标量响应；(2)带有标量协变量的函数响应；(3)具有函数协变量的函数响应；(4)具有函数和标量协变量的标量或函数响应。目前，函数回归算法的研究主要集中在模型的优化和计算效率上，而基于函数回归的隐私保护研究还少有人涉足。Janet S. Kim等人[3]于2018年提出一种加性的函数对函数回归算法，Mark等人[4]针对该模型提出离散小波包变换的算法。针对高维的加性函数模型中mFPCA分数的估计误差问题，Wong等人[5]提出了一类部分线性泛函可加模型(PLFAM)。该文提出一种函数对函数回归的差分隐私保护算法，即计算函数回归，在回归的过程中加入满足差分隐私的拉普拉斯噪声，以达到隐私保护的作用。

主要贡献如下：

(1)结合函数回归和差分隐私保护的拉普拉斯机制，设计了一种满足ε-差分隐私保护的函数回归算法，并通过理论分析和实验验证其可用性。

(2)使用B样条基对函数型数据进行降维和回归处理，允许观测数据含噪，在实现函数回归的基础之上，保证了一定的隐私保护功能。

(3)针对不同隐私预算进行实验，证明隐私预算ε与算法效率的关系，且添加噪声越小，算法效率越高。

1 相关工作

本节主要介绍差分隐私和函数回归相关的研究工作。

Dwork[6]于2006年提出了差分隐私的概念，区别于传统的k-匿名等隐私模型，差分隐私保护模型具有强大的数学模型和坚实的算法设计基础，它可以严格地定义和计算隐私的保护水平，有利于比较和研究在不同参数下的保护水平。目前，差分隐私的机制仍在逐步完善中[7-9]。

Ramsay和Dalzell[10]于1991年提出了一种函数对函数的回归线性模型，将函数预测器和函数响应回归设置中存在的问题结合在一起，Yao等人[11]设计了该模型基于函数主成分(Functional Principal Component，fPC)的方法，假设协变量和响应具有独立同分布的测量误差，并用fPC分解进行建模。Wu & Müller[12]在估计回归系数时使用WLS来解释函数内的相关性。文献[13]将函数线性模型扩展到函数可加模型(Functional Addictive Model)，该模型通过协变量的函数主成分得分的平滑函数之和对协变量的影响进行建模。Janet S. Kim等人[3]在加性函数对函数的回归中提出了一种当前响应与协变量的完整轨迹相关联的非线性回归模型，可以更直接地捕获响应与完整协变量轨迹之间的复杂关系。

Mark等人[4]提出了一种使用离散小波包变换的函数对函数回归模型，适合无约束曲面，但是不适合建模滞后暴露的功能预测因子。Wong等人[5]改进了高维加性函数模型中mFPCA分数的估计误差，提出了一类部分线性泛函可加模型(PLFAM)。

迄今为止的大多数函数回归研究都假设存在独立同分布的测量误差，但是没有考虑到为观测对象进行隐私保护，也没有考虑实现满足差分隐私的加噪扰动。

2 理论基础

2.1 差分隐私保护技术

差分隐私保证受保护的数据集不会因为增加或删除一条记录而影响查询结果[14]。其形式化的数学定义如下：

定义1(差分隐私)[15]：给定邻近数据集(只相差一条记录)D和D'，设有隐私算法A，Range(A)为A所有可能的输出结果，若算法A在数据集D和D'上任意输出结果O(O∈Range(A))满足下列不等式：

Pr[A(D)=O]≤eε×Pr[A(D')=O]

(1)

则称算法A满足ε-差分隐私，ε的值称为隐私预算，ε越小，A(D)=O和A(D')=O的概率值越接近，算法A的隐私保护水平越高。

差分隐私算法满足以下组成属性。假设A1(·)和A2(·)是ε1-和ε2-差分隐私算法。

·顺序合成：释放A1(D)和A2(D)的输出满足ε1+ε2-差分隐私。

·后处理：对于任何算法A3(·)，释放A3(A1(D))仍然满足ε1-差分隐私。即对差分隐私算法的输出进行后处理不会导致任何其他隐私损失。

定义2(全局敏感度)[6]：函数f：D→Rn的全局灵敏度(表示为Δ(f))定义为来自任意两个相邻数据集D1和D2的输出的最大L1距离：

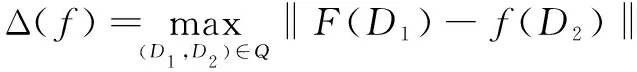
(2)

其中，R表示所映射的实数空间，d表示函数f的查询维度。全局敏感度只与函数f有关，与数据集D无关。

差分隐私保护有两种常用的实现机制：Laplace机制和指数机制。该文采用的是Laplace机制。Laplace机制的实现方式是通过添加满足Laplace分布的随机噪声来达到ε-差分隐私保护的效果。

定义3(Laplace机制)[15]：对于任意一个函数f：D→Rd，若算法K的输出结果满足等式(3)，则K满足ε-差分隐私：

K(D)=f(D)+〈Lap1(Δf/ε),…,Lapd(Δf/ε)〉

(3)

其中，Lap1(Δf/ε)(1≤i≤d)是相互独立的拉普拉斯变量，由上式可得：噪声大小与Δf成正比，与ε成反比。

2.2 函数型数据分析

函数型数据分析(Functional Data Analysis)是对曲线、曲面或任何其他连续变化的信息的一种统计分析方法，其协变量或响应为函数型数据[16]。函数型数据研究的对象是光滑曲线，例如{xn(t):t∈[T1,T2]},1≤n≤N；其中xn(t)∈R在每一点t∈[T1,T2]都存在，取观测点{tj,n:1≤j≤Jn}。如下为一个典型的函数型数据集：

{xn(tj,n)∈R:tj,n∈[T1,T2],1≤n≤N,1≤j≤Jn}

如果每条曲线的观测数Jn都很小，则称此函数型数据稀疏(sparse)；例如血检得到的某蛋白浓度。如果每条曲线的观测数Jn都很大，则称此函数型数据密集(dense)；例如地磁仪记录的某地磁场强度，高频交易的股票价格[17]。

3 函数回归的差分隐私保护算法

本节包括函数回归的差分隐私保护算法的各部分概述及具体实现细节，并给出算法实现差分隐私保护的证明。

3.1 场景描述

对于i=1,2,…,n，假设{(Xik,sik)：k=1,2,…,mi}，{(Yij,tij)：j=1,2,…,mY,i}，其中Xik和Yij分别是在时间点sik和tij观察到的协变量和响应。对于所有i和k，sik∈ΓX，以及所有i和j，tij∈ΓY，其中ΓX和ΓY是紧凑的时间间隔。假设Xik=Xi(sik)，其中Xi(·)是定义在ΓX上的平方可积、真平滑信号。同时假设Yij=Yi(tij)，其中Yi(·)定义在ΓY上。

考虑一个加性的函数对函数回归模型：

(4)

其中，F{.,.,t}是定义在R×ΓX×ΓY上的未知平滑三变量函数，εi(·)是一个误差过程，具有均值为零和未知的自协方差函数R(t,t')，并且与协变量Xi(s)无关。函数F{·,·,t}的定义量化了当前响应Yi(t)和完整的协变量轨迹Xi(·)之间的未知相关性，而加性模型则允许对高维数据空间的响应和协变量之间的关系进行非参数建模。

如果F(x,s,t)=β(s,t)x，则模型(4)简化为标准函数线性模型。

3.2 数据预处理

由于实际观测的数据存在噪声或测量误差，在数据预处理阶段，需要对离散的响应和协变量进行平滑处理，使之从离散的多元观测变量变成内部存在关联的函数型数据。

对模型(4)中的F进行建模，为了降低计算成本，减少基函数的数量，令φ(·)∈L2(ΓY)为一平滑函数，则Yi到φ(·)的投影为：

结合模型(4)可推出：

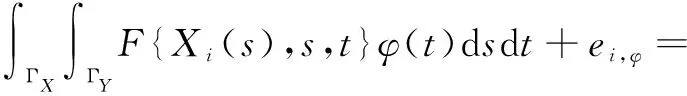
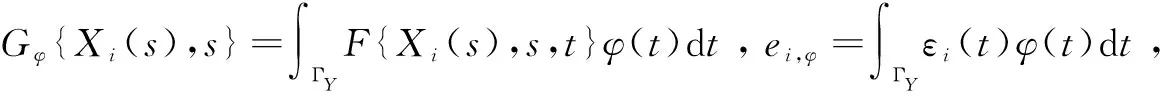
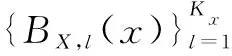
其中，θl,l',k是未知参数。因此，模型(4)的三变量函数F可由x和s方向上的单变量B样条基函数和L2(ΓY)正交基函数φk(·)的张量积获得，由于只考虑两个样条基，减少了所需的基函数和平滑参数，降低了计算成本，可以有效提高计算效率。

3.3 DP-in-FRA算法思路

函数回归的差分隐私保护算法(Differential Privacy Preservation Algorithm in Functional Regression)简称DP-in-FR。

(6)

未知参数Θk的取值使用惩罚最小二乘法估计，对方向x和s使用二次惩罚，并通过正交基函数的数量K控制t方向的粗糙度。由计算可得，x的方向曲率为：

∭{∂2F(x,s,t)/∂x2}dxdsdt=

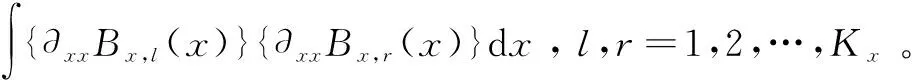
∭{∂2F(x,s,t)/∂s2}dxdsdt=

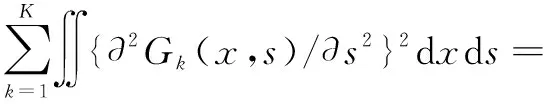
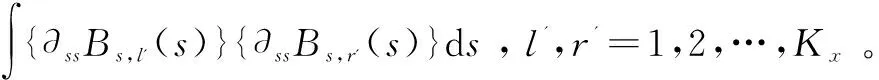
则最小化的惩罚标准是：

IKx+λxIKx⊗Ps)Θk=

(7)

DP-in-FR对回归模型的系数进行噪声扰动。 具

(8)

全局敏感度的推导与计算过程如下：

对于邻近数据集D和D'，以及它们的代价函数fD和fD'：

根据全局敏感度的定义(见定义2)有：

由此，可以得到全局敏感度Δ为：

(9)

将该算法记为算法1，其算法流程如下：

算法1：DP-in-FR。

输入：原始数据集D，隐私预算，主成分预设值p；

2：使用函数数据主成分分析(FPCA)估计Yi(·)的(边际)协方差的特征基φk(·)；

6：for 1≤k≤Kdo

8：end for

3.4 隐私性分析

定理1：算法1满足ε-差分隐私保护机制。

综上所述，算法1满足ε-差分隐私保护机制，实现了对数据的隐私保护功能。

4 实验与分析

4.1 实验环境

实验环境为AMD Ryzen 7 5800H with Radeon Graphics3.20 GHz，16G内存，Win10操作系统。算法均采用R语言实现，R语言版本为R-4.1.0，RTools版本4.0，使用到的程序包有MASS、Matrix、refund、mgcv、VGAM等。其中VGAM版本为1.1-5，用于产生符合拉普拉斯分布的随机噪声。

数据集的具体信息如表1所示，分别为加拿大天气数据集、LipEMG数据和扩散张量成像(DTI2)数据。以上数据集分别来自文献[18-19]。表1显示了数据集的统计信息，其中|S|和|T|是相应域中的数据/时间点个数。

表1 数据集信息

为了验证所设计算法的可行性，在这三个数据集上，依次使用文中算法进行训练，通过训练结果的精确度来判断其可用性。此外，为了检测隐私预算ε对模型准确性的影响，对每个数据集也以不同的隐私预算ε进行多次训练。由于噪声的影响，会进行多次实验取结果的均值。

4.2 实验结果及分析

回归分析有多种性能指标衡量其精确性，该文使用的性能指标是均方根预测误差(RMSPE)以及逐点预测区间的平均覆盖概率(ACP)。通过以下方式定义RMSPE：

RMSPE=

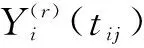
实验结果如图1所示。

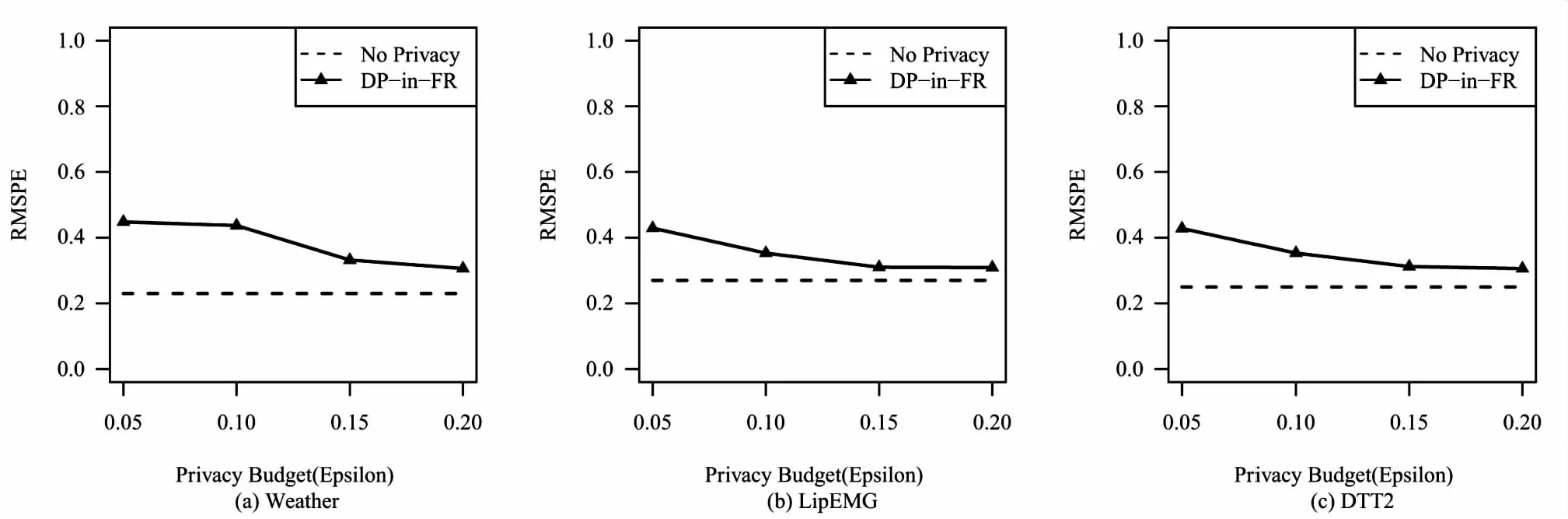
图1 均方根预测误差

图1(a)、(b)、(c)分别是文中算法对三个数据集在不同隐私预算ε下训练结果的准确性的比较，ε的取值范围为{0.05,0.1,0.15,0.2}。横坐标是隐私预算ε的取值，纵坐标是均方根预测误差RMSPE。标签中，No Privacy即不添加任何隐私保护机制的函数回归，它将作为算法精确性的比较基准。三个数据集的训练结果均遵循隐私预算越大，训练出的模型精确度越高的规律，并且当隐私预算足够大时，与无隐私保护的算法的精确度接近。

其次，对(1-α)水平点态预测区间进行近似，以观察名义水平上的覆盖概率。在(1-α)级别定义预测区间的ACP如下：

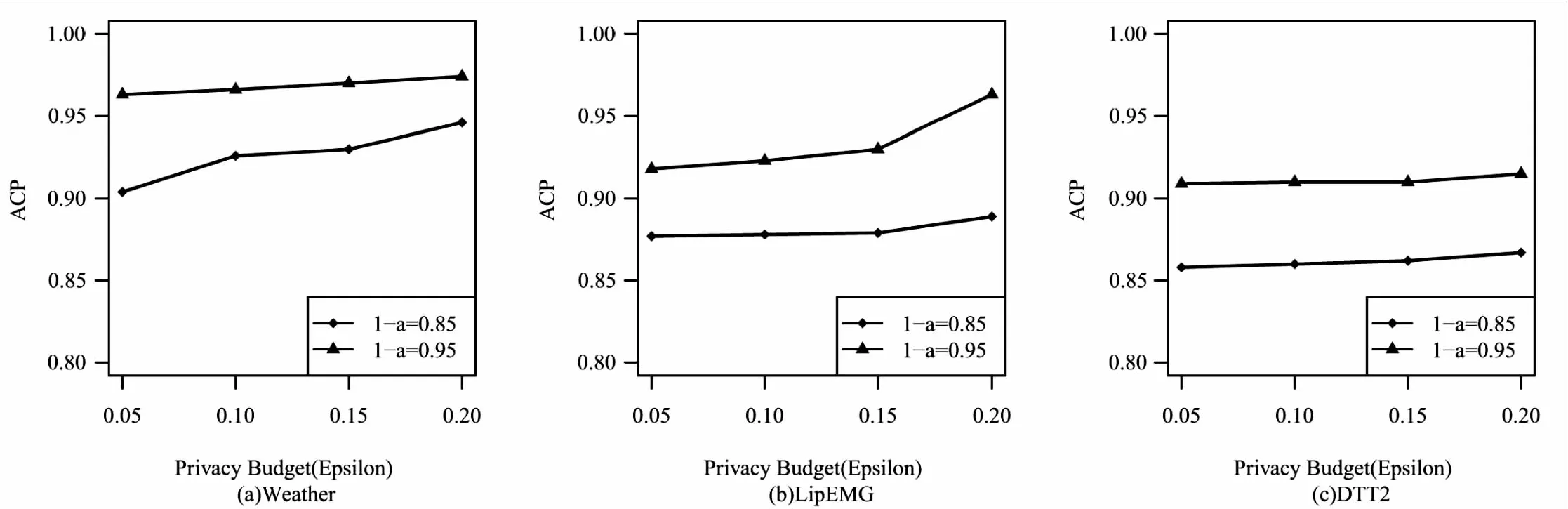
图2 平均覆盖率

图2(a)、(b)、(c)分别为在1-α=0.85和0.95的名义显著性水平下，预测响应Y(t)|X(·)在三个数据集上的平均覆盖概率ACP得分。可以看见随着隐私预算ε增大，DP-in-FR算法预测平均覆盖率从整体上看有升高的趋势，这是因为随着ε增大，隐私保护程度变低，添加的噪声变小，所以可用性变高，因此预测准确率变高。

5 结束语

主要研究了差分隐私在函数回归中的应用，设计了一种基于差分隐私的函数回归方法。该方法允许观测数据含噪，对函数型数据进行降维和回归处理，在实现函数回归的基础之上，保证了一定的隐私保护功能。该文提出的函数回归算法对于输入数据降维并提取主成分，而隐私预算大小和保留主成分的个数是影响算法误差的因素，合理的加噪方式使得数据可用性更高。由于函数型数据回归的计算量大，计算成本高，所以更合理的隐私预算分配和加噪方式以提高计算效率是下一步的研究方向。