基于线圈子单元的永磁同步电机健康与定子绕组短路故障数学模型

高彩霞 苗 壮 陈 昊 司纪凯 吕 珂

（1.河南理工大学电气工程与自动化学院 焦作 454003 2.河南理工大学应急管理学院 焦作 454003 3.郑州大学电气工程学院 郑州 450001 4.海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033）

0 引言

近年来，永磁同步电机（Permanent Magnet Synchronous Motor,PMSM）因其高转矩/惯量比、高功率密度、高效率、响应快等优点，被广泛应用于电动汽车、轨道交通、航空航天等领域[1-3]。PMSM在长期运行过程中，受到热应力、电应力、机械应力等因素影响[4-5]，定子绕组容易因绝缘损坏而引发匝间短路故障（Interturn Short-circuit Fault,ISF）[6-7]。如果早期ISF 没有被及时监测到并采取相应措施，会迅速发展成多线圈短路故障、相间短路故障等更严重的故障，甚至可能引发灾难性事故[8-9]。定子绕组短路故障（Winding Short-circuit Fault,WSF）的精准诊断是提高电机可靠性、安全性和经济性的重要手段。建立模型对电机故障前后的性能分析并遴选故障特征量，是故障诊断的基础。目前，大量文献通过建立电机WSF 数学模型，实现对电机健康和WSF 状态的分析[10-17]，但它们不能有效考虑绕组结构与故障空间位置的影响，难以分析线圈对电机性能的贡献及线圈内部不同位置短路故障对电机性能的影响。因此，有必要建立一个考虑绕组结构与故障空间位置影响的PMSM 健康状态与WSF 的数学模型。

目前，已有许多学者对电机WSF 模型进行了广泛而深入的研究，并取得一些重要成果。文献[10-13]采用绕组分区法，把故障相绕组分为健康和故障部分，以相绕组为基本单元计算模型参数，并建立电机短路故障模型。对健康状态分析时，该类模型仅能分析相绕组的电压、电流等参数；对故障状态分析时，该类模型忽略了相内故障空间位置的影响，无法区分相内不同位置ISF 对电机性能的影响。文献[14-16]从单个线圈出发计算电感和空载反电动势参数，再通过叠加得到实际回路的电感和空载反电动势参数，并根据电机的实际回路建立多回路模型。文献[14-16]不仅分析了健康状态时线圈对电机性能的贡献，也分析了支路内部不同位置ISF 对电机性能的影响。文献[17]基于分区法将相绕组分成多个线圈，并以线圈为基本单元，在Matlab/Simulink 中建立和求解模型。对健康状态分析时，该模型仍把相绕组作为一个整体，计算线圈的空载反电动势，忽略了线圈位置对空载反电动势的影响，难以准确分析线圈对电机性能的贡献；对故障状态分析时，该模型能够方便、快速地分析不同类型的WSF，但仍忽略了线圈内部故障线匝位置的影响。文献[18-21]建立了电机 WSF 的有限元模型（Finite Element Model,FEM），可以精确分析健康的及不同类型的WSF 下的电磁特性。FEM 考虑了故障空间位置、绕组结构等因素的影响，不仅能分析健康状态时线圈对电机性能的贡献，还能区分线圈内部不同位置ISF 对电机性能的影响。但FEM 对不同短路故障分析需要重新建模，而且其求解过程耗时。

为了在较短的时间内计算电机健康的和不同类型定子绕组短路故障下的电磁特性，并考虑电机绕组结构与故障空间位置影响，本文将每个线圈分割为多个线圈子单元，以线圈子单元为基本单元，建立一个基于线圈子单元的PMSM 健康与WSF 数学模型（A PMSM Mathematical Model,APM）。

本文的主要贡献为：①在Matlab/Simulink 中建立APM 的仿真模型和图形化界面，通过修改抽头编号及图形化界面中短路电阻模块的连接位置，方便、快捷地计算电机健康和不同类型定子绕组短路故障下的电磁特性。②考虑了电机绕组结构的影响，APM 能够准确分析健康状态时线圈对电机性能的影响。③考虑了故障空间位置的影响，APM 能够准确分析线圈内部不同位置短路故障对电机性能的影响。

1 基于线圈子单元的PMSM 数学建模

1.1 基于线圈子单元的PMSM 数学模型

为了高效、准确、精细化分析电机在健康及不同类型WSF 状态下的电磁性能，本文建立一个基于线圈子单元的PMSM 健康与WSF 数学模型，其电路示意图如图1 所示。

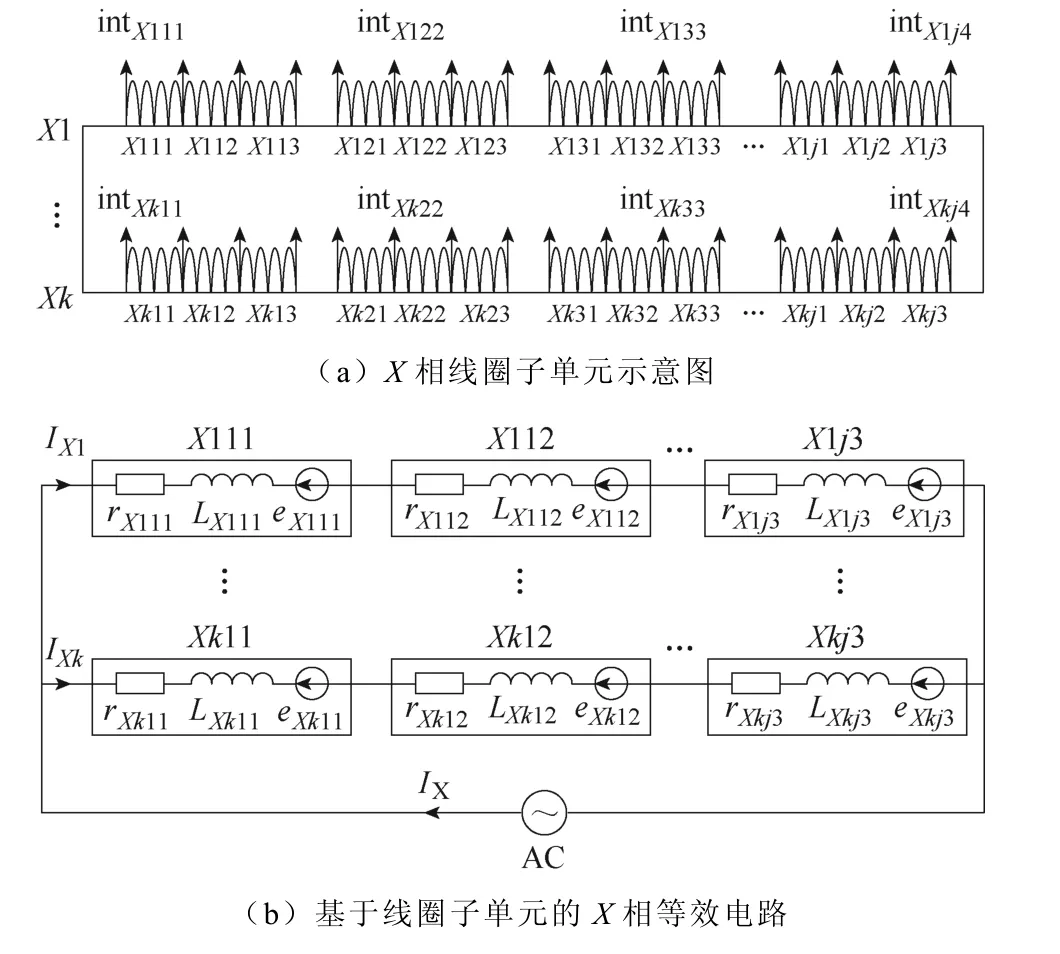
图1 PMSM 电路示意图Fig.1 The circuit diagram of PMSM

该APM 将每个线圈分为三个线圈子单元，并引出四个抽头intXkjz如图1a 所示，其中intXkj1和intXkj4为固定抽头，intXkj2和intXkj3为可变抽头。子单元的匝数随可变抽头位置的变化而变化，可变抽头的位置取决于待分析的短路故障的位置和匝数。根据上述划分规则，基于线圈子单元的等效电路如图1b 所示，其中每个子单元具有各自的电阻、电感及空载反电动势，在电机健康状态下，由同一线圈分割而成的三个子单元的空载反电动势、电感及电阻之和分别等于未分割线圈的空载反电动势、电感及电阻。

为简化分析，忽略涡流、磁滞损耗以及趋肤效应；电机铁心磁导率为无穷大；电机磁路为线性的。基于以上假设，该APM 的表达式为

式中，Vs、Rs、Is、Ls和E0分别为电压矩阵、电阻矩阵、电流矩阵、电感矩阵和空载反电动势矩阵。vXkjw、iXkjw、rXkjw、eXkjw、LXkjw分别为子单元Xkjw的瞬时电压、瞬时电流、电阻、瞬时空载反电动势、瞬时自感。MXkjwYmno为子单元Xkjw与子单元Ymno之间的瞬时互感。Pe、P1、pCu和pFe分别为瞬时电磁功率、输入功率、定子铜耗和铁耗（根据建模假设，铁耗忽略不计）。Pe.ac、Tave、f、n和Ω分别为电磁功率平均值、电磁转矩、电源频率、转速和机械角速度。其中X、Y代表相编号，k、m代表支路编号，j、n代表线圈编号，w、o代表子单元编号，z代表抽头序号（X,Y=A,B,C,…；k、m=1,2,3,…；j,n=1,2,3,…；w,o=1,2,3；z=1,2,3,4；Xkjw≠Ymno）。基于式（1）～式（12），在Matlab/Simulink环境下的图形化界面中建立APM 仿真模型，如图2所示。

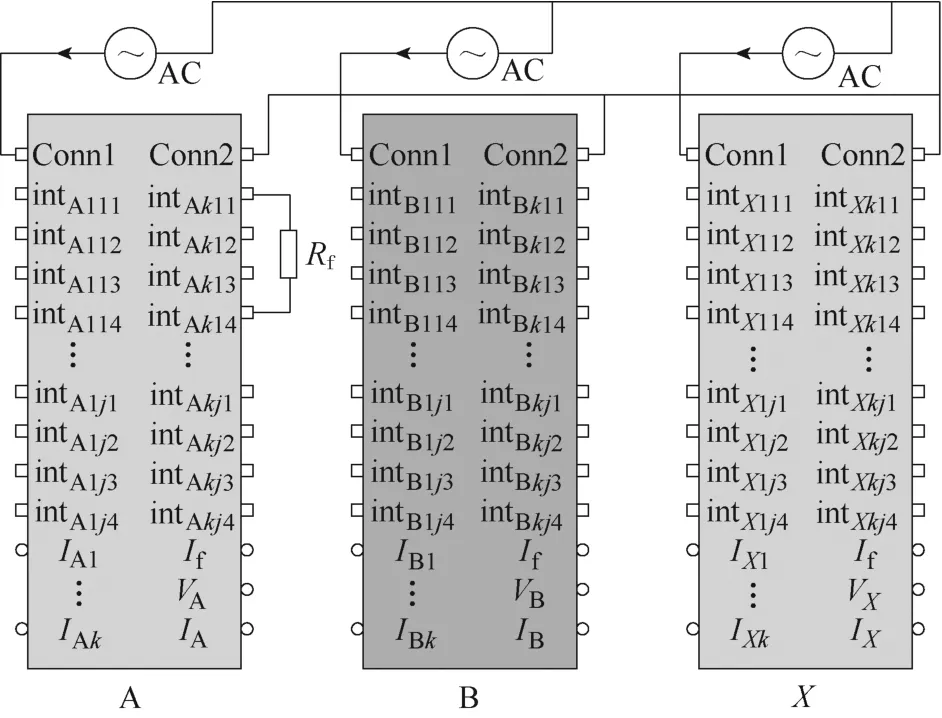
图2 建立的APM 仿真模型Fig.2 The established APM simulation model

图2 所示的APM 仿真模型由交流电源AC、子单元电阻、子单元电感、短路电阻Rf、电流传感器、电压传感器等模块构成，其中IXk、If、VX、IX分别为测量Xk支路电流、短路电流、X相电压、X相电流的传感器端口。在分析电机健康状态性能时，只需要将图2 的Rf开路，通过电源模块输入交流电源的幅值及频率设置运行工况，通过传感器模块获取相绕组和各线圈的电压、电流等参数，进而分析不同位置线圈对电机性能的贡献。对WSF 分析的步骤如下：

（1）设置运行工况：通过交流电源的幅值及频率模拟电机的负载及转速情况。

（2）设置不同的WSF：将Rf并联到图2 所示的相应的抽头之间，完成WSF 的短路电阻、短路匝数及短路位置的设置，具体设置方式如下：

1）模拟槽口处发生ISF（短路匝数Nf＜线圈匝数Nc），将Rf连接到抽头intXkj1和intXkj2之间。

2）模拟槽底处发生ISF（Nf＜Nc），将Rf连接到抽头intXkj3和intXkj4之间。

3）模拟单线圈短路时（Nf=Nc），将Rf连接到抽头intXkjz和intXknz（j≠k）之间。

4）模拟相间短路故障，将Rf连接到抽头intXkjz和intYkjz（X≠Y）之间。

（3）设置intXkj2和intXkj3的编号；沿槽深位置依次对定子线圈的线匝进行编号，如图3 所示。

图3 线匝位置编号Fig.3 The position number of coil turns

根据待分析的短路类型、位置及匝数输入可变抽头intXkj2和intXkj3的编号。子单元的匝数由intXkj2和intXkj3的编号自动确定，其电阻rXkjz、瞬时空载反电动势ec和瞬时电感分别由式（13）、式（15）、和式（20）自动计算。

式中，rc为单个线圈的电阻。ec为单个线圈的瞬时空载反电动势矩阵。ep为编号为p的线匝的瞬时空载反电动势。C为位置矩阵，位置矩阵第1 行第1列至第intXkj2列数值为1，其余列为0；第2 行第intXkj2+1 列至第intXkj3列数值为1，其余列为0；第3 行第intXkj3+1 列至第intXkj4列数值为1，其余列为0。使用时输入可变抽头intXkj2和intXkj3的位置编号，可自动生成位置矩阵。eXk1w-h和αh为子单元Xk1w的瞬时空载反电动势第h次谐波分量的幅值和初相角。β为相邻线圈在空间上相隔的电角度。结构正常的永磁体（不考虑退磁故障）产生空载反电动势的空间周期为1 对极，空载反电动势只包含基波和3、5 等奇数次谐波[15]，即h=1,3,5,…。

（4）通过Simulink 环境下的传感器模块获取短路电流、支路电流、子单元电压、线圈电压、相电压等参数，并通过式（7）～式（12）计算功率及转矩。

在分析不同类型定子绕组短路故障时，传统数学建模方法需要改变模型的拓扑结构并重新建立方程；所提出的APM 只需要根据短路类型、位置及匝数在仿真模型的图形化界面中修改抽头编号及短路电阻模块的连接位置，具有方便、快速的优点。

1.2 考虑空间位置的电感计算

由于相同槽中不同位置线匝交链的槽漏磁通不同，所以相同槽、相同匝数、不同位置线圈的电感和空载反电动势也不同。对于图3 中线圈匝数为Nc的电机，对应的线匝电感计算为

式中，Lp为位置编号为p的线匝的瞬时自感；Mpp＇为同一线圈内编号为p的线匝与编号为p＇的线匝之间的瞬时互感；Mpp＇为线圈Xkj内编号为p的线匝与线圈Ymn内编号为p＇的线匝之间的瞬时互感；ψp为位置编号为p的线匝和永磁体共同在编号为p的线匝上产生的瞬时磁链；ψp＇为位置编号为p的线匝和永磁体共同在编号为p＇的线匝上产生的瞬时磁链；ψp＇为位置编号为p的线匝和永磁体共同在编号为p＇的线匝上产生的瞬时磁链；ψPMp、ψPMp＇和ψPMp＇为永磁体分别在位置编号为p、p＇和p＇的线匝上产生的瞬时磁链；i为通入位置编号为p的线匝的直流电流。

在线圈电感的有限元计算模型中，将1 A 的直流电通入到编号为p的线匝来计算Lp、Mpp＇和Mpp＇。为了减小电感计算的工作量，首先利用FEM计算出奇数线匝瞬时电感，其次利用拟合法计算出剩余线匝瞬时电感，即

最后通过变换矩阵计算出所有子单元电感为

2 有限元仿真验证

2.1 PMSM 关键参数

为了验证APM 的正确性和准确性，本文以一台电流源供电的 66 极72 槽星形联结的三相面贴式PMSM 为研究对象。其定子绕组采用分数槽集中绕组隔齿绕的型式。PMSM 的关键参数见表1。

表1 PMSM 的关键参数Tab.1 The key parameters of PMSM

2.2 健康状态的解析与有限元结果比较分析

为了验证所建立的APM 在健康状态时不同工况下对电机性能分析的正确性与准确性，对由两种转速情况（n=100,200 r/min）和三种负载情况（IX=14,28,42 A）组成的六种工况下的电机性能进行比较分析。进行对比的六种工况列于表2 中。

表2 进行对比的工况Tab.2 The compared conditions

表3 为不同工况下APM 与FEM 计算出的平均转矩及其误差。

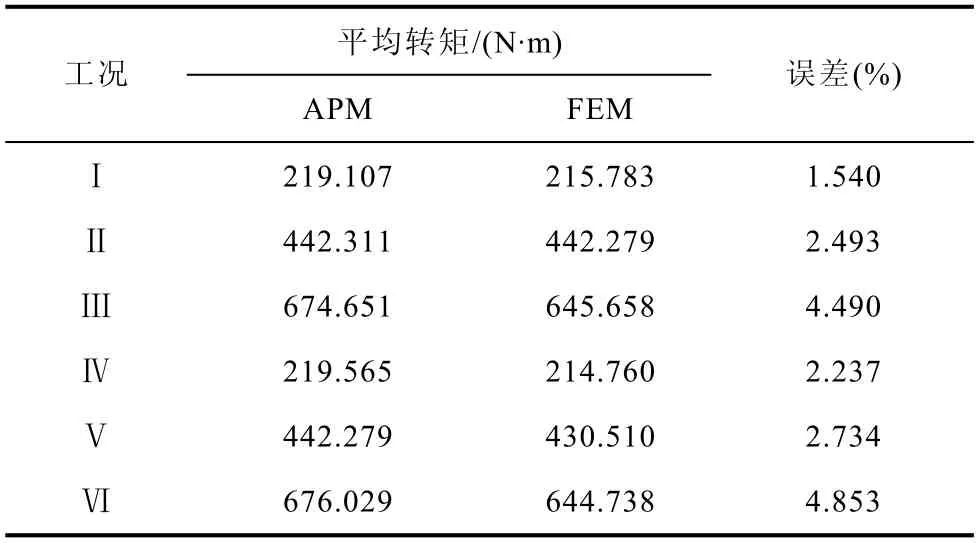
表3 平均转矩Tab.3 The average torque

由表3 可知，APM 计算出的平均转矩略微大于FEM 计算出的平均转矩，最大误差约为4.85 %，该误差是由于建模时忽略铁耗和磁路饱和引起的。

表4 为不同工况下APM 与FEM 计算出的A 相电压VA峰峰值及其误差。

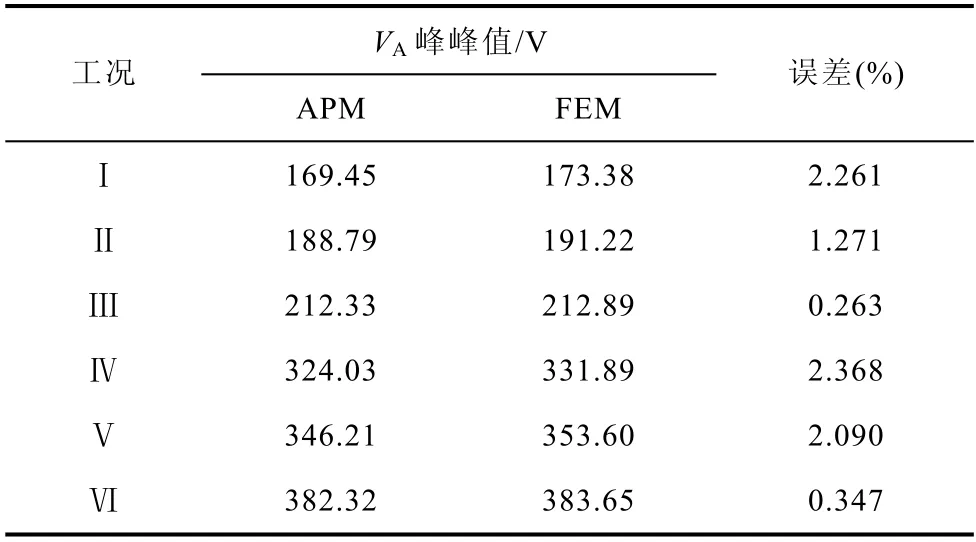
表4 VA 的峰峰值Tab.4 The peak-peak value of VA

由表4 可知，APM 计算出的VA的峰峰值略微小于FEM 计算出的VA的峰峰值，最大误差约为2.4 %，该误差主要是由于建模时忽略磁路饱和引起的。

表5 为不同工况下APM 与FEM 计算出的Xk1线圈、Xk2 线圈电压VXk1、VXk2峰峰值及其误差。

由表5 可知，APM 与FEM 计算出的线圈电压峰峰值的最大误差约为2.2 %。Ak2 线圈的电压高于Ak1 线圈的电压，说明电机运行时Xk2 线圈比Xk1线圈产生的功率多，这是由于两类线圈空载反电动势相位不同造成的。因此，Xk（jj=2、4）和Xkn（n=1、3）线圈可以设计成不同的绝缘等级，提高使用寿命，降低制造成本。与工况Ⅳ的VAk1相比，工况Ⅴ的VAk1和工况Ⅵ的VAk1分别增加了1.9 %和7.6 %，与工况Ⅳ的VAk2相比，工况Ⅴ的VAk2和工况Ⅵ的VAk2分别增加了10.4 %和22.3 %，Xk2 线圈比Xk1 线圈对负载变化更敏感，说明电机运行时Xk2 线圈比Xk1 线圈承担的负载多。在恒定的转矩负载下，Xk2 线圈故障时对电机性能的影响大于Xk1 线圈故障时。当APM 仿真模型完成建模后，对健康状态分析时，单次仿真计算需要2.3 s，而相同条件下FEM 的单次仿真计算需要4 141 s，APM 可以快速地对电机健康状态进行分析。

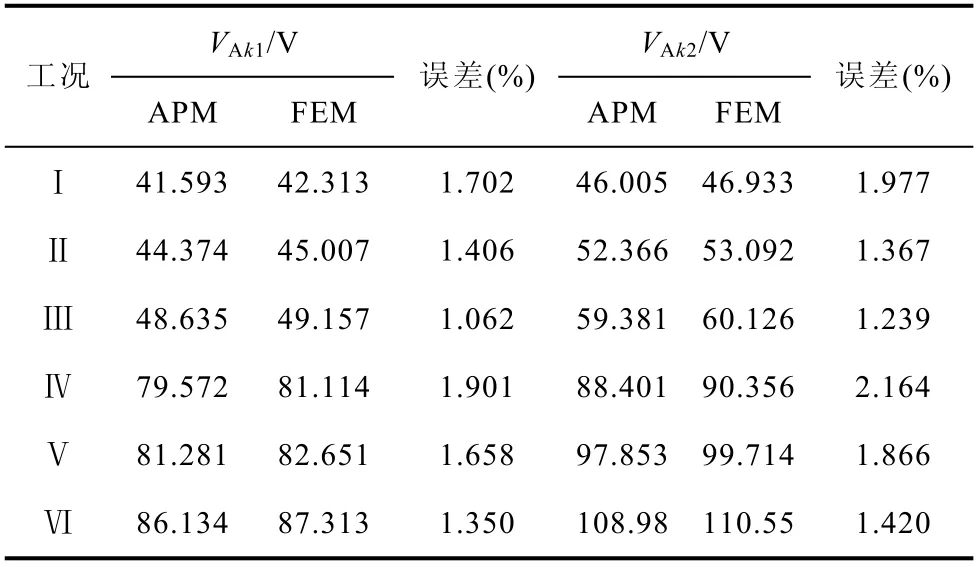
表5 VXk1、VXk2 的峰峰值Tab.5 The peak-peak value of VXk1,VXk2

因此，有限元仿真验证了所提出的APM 不仅能精确、高效地分析健康状态时电机在不同工况下的相电压、线圈电压、平均转矩等电磁特性，还能精细地分析线圈对电机性能的贡献。利用APM 对不同位置的线圈进行分析，能够发现同一支路不同位置线圈的电压不同，功率不同，承担的负载也不同。在设计线圈绝缘时，为降低电机制造成本，同一支路不同位置线圈采用不同的绝缘等级。上述分析为PMSM 的本体设计提供依据。由于同一支路不同线圈的电压不同，在线圈绝缘等级相同的情况下，同一支路不同线圈的故障概率不同；线圈内部同一短路匝数不同短路位置故障对电机性能的影响也不相同。上述分析可为PMSM 的故障诊断提供依据。

2.3 WSF 状态的解析与有限元结果比较分析

为了验证APM 在不同WSF 下特性分析的正确性与准确性，对三类WSF 下的电机电磁特性进行比较分析。仿真分析的故障类型列于表6 中，电机运行在额定工况下（n=200 r/min，IX=28 A）。

表6 仿真分析的故障类型Tab.6 Fault types of simulation analysis

A12_01～48 表示A12 线圈48 匝短路故障，为分析该故障，将Rf并联在A12 线圈的抽头intA121和intA124之间。A11_01～24 和A11_25～48 分别为A11 线圈槽口处和槽底处24 匝短路，槽口24 匝短路时将抽头intA112的值设置为24，并将Rf连接在抽头intA111和intA112之间；槽底24 匝短路时将抽头intA113的值设置为25，并将Rf连接在抽头intA113和intA114之间。A34.48_C34.48 表示A34 线圈与C34线圈间发生相间短路故障，为分析该故障，将Rf并联在A34 线圈的抽头intA341和C34 线圈的抽头intC341之间。

图4 所示为 PMSM 分别在 A12_01～48、A11_01～24 及A11_25～48 故障状态下由APM 与FEM 计算出的VA、IA1、If和平均转矩Tave随Rf的变化曲线。

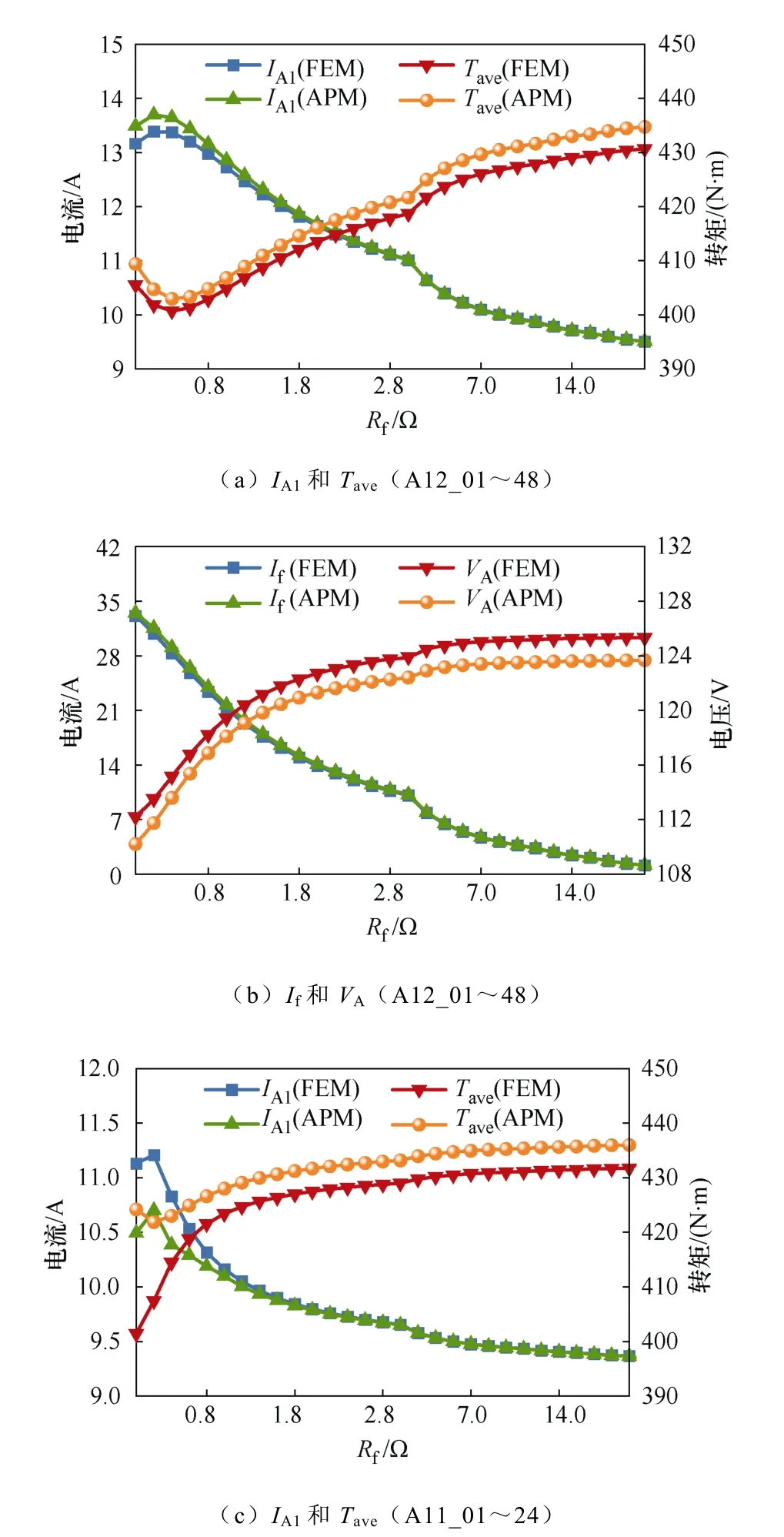
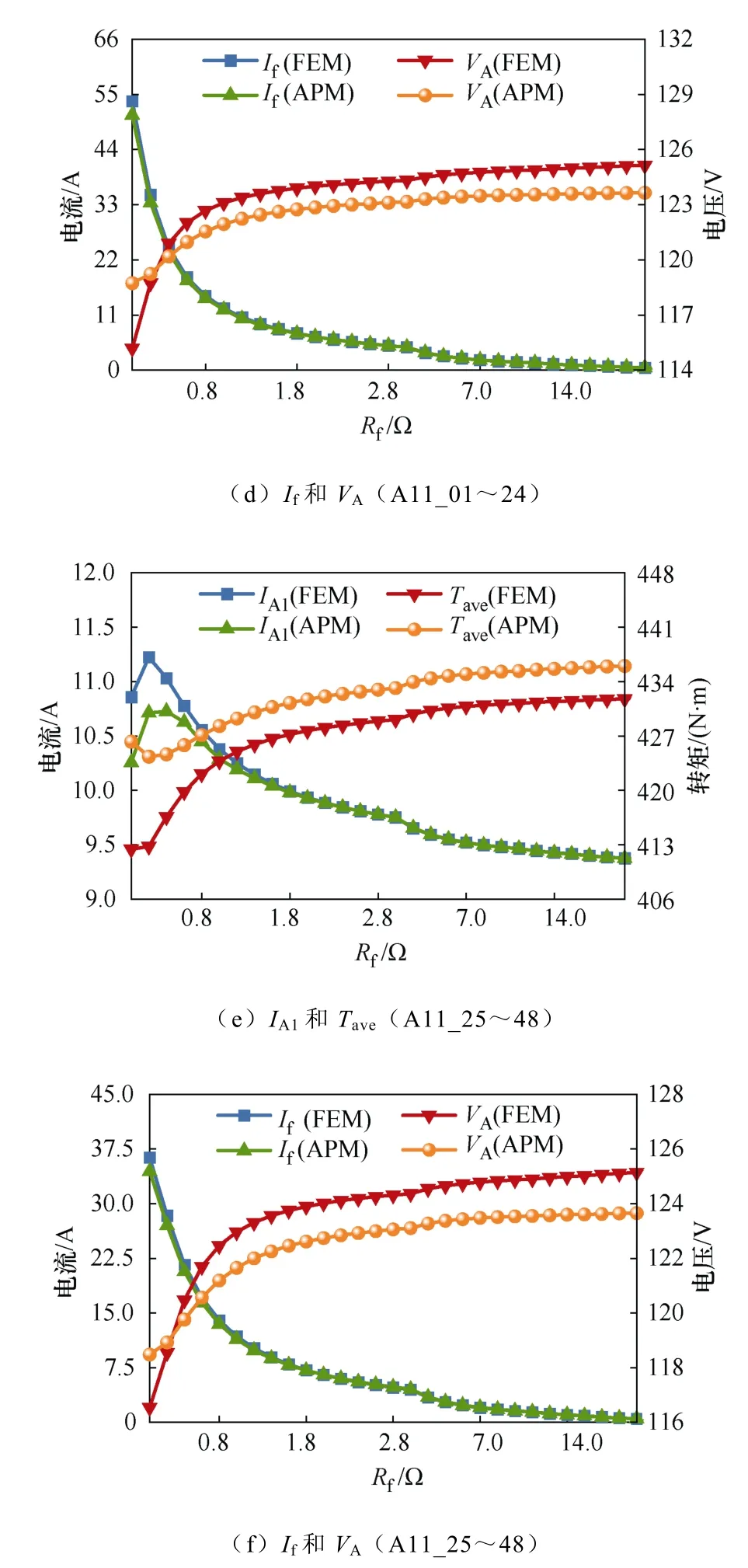
图4 不同故障下APM 结果与FEM 结果比较Fig.4 Comparison between APM results and FEM results under different faults

由图4a 和图4b 可知，APM 与FEM 计算结果吻合度较好，A12_01～48 故障情况下，最大误差约为3.0 %。该误差是由于建模时忽略磁路饱和与铁耗引起的。有限元仿真证明了APM 能够分析单线圈ISF，并且具有较高的精度。

由图4c～图4f 可知，APM 与FEM 计算结果吻合度较好，A11_01～24 故障情况下，最大误差为5.7 %；A11_25～48 故障情况下，最大误差为5.5 %。该误差是由于建模时忽略磁路饱和与铁耗引起的。有限元仿真证明了APM 能够分析线圈内部ISF，并且具有较高的精度。

图5 为PMSM 在A34.48_C34.48 故障状态下由APM 与FEM 计算出的VA、C 相电压VC、A3 支路电流IA3、C3 支路电流IC3、If和Tave随Rf的变化曲线。

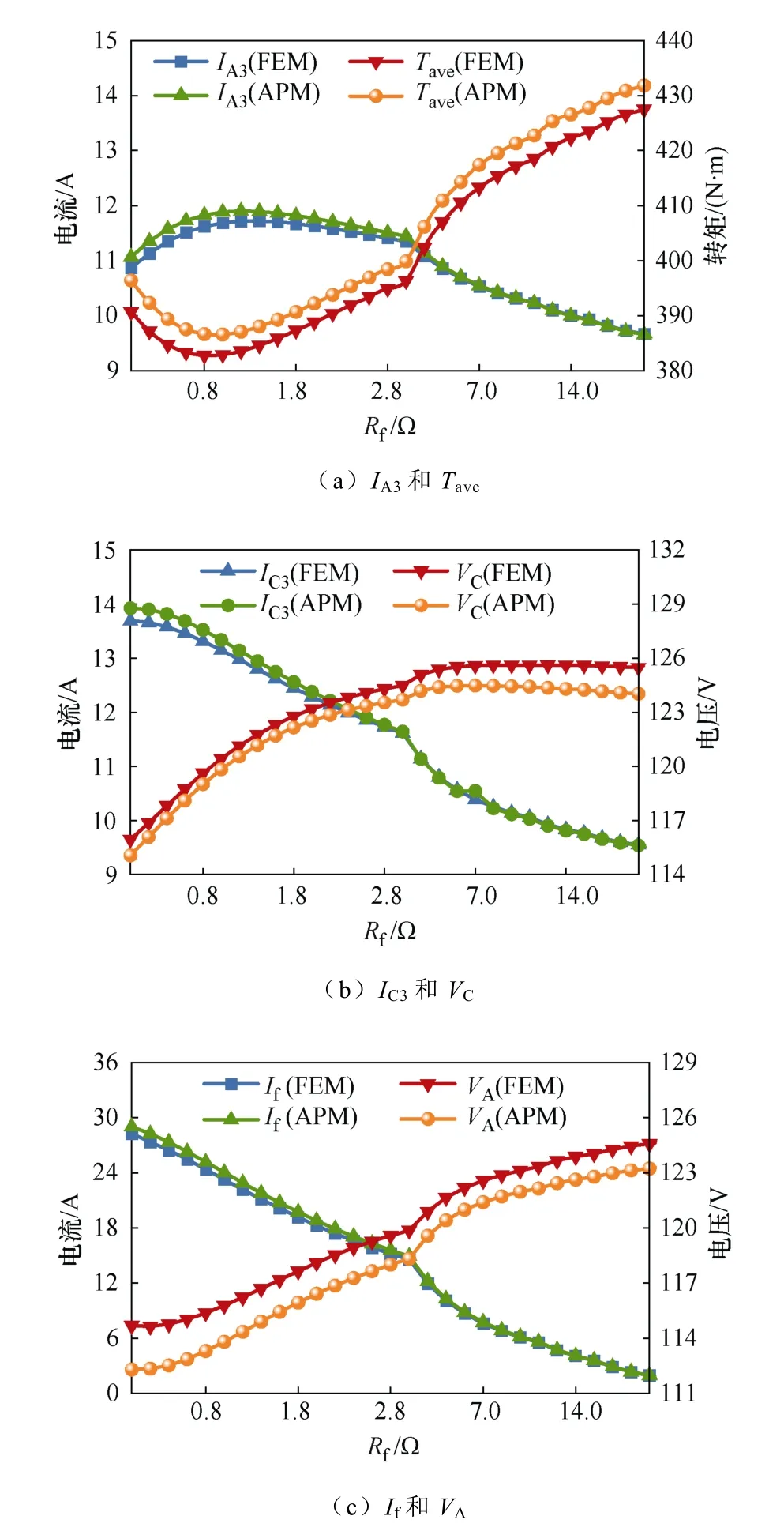
图5 A34.48_C34.48 下APM 结果与FEM 结果比较Fig.5 Comparison between APM results and FEM results under A34.48_C34.48

由图5 可知，APM 与FEM 计算结果吻合度较好，A34.48_C34.48 故障情况下，最大误差约为4.0 %。该误差是由于建模时忽略磁路饱和与铁耗引起的。有限元仿真验证了APM 也适用于分析相间短路故障，并且具有较高的精度。

图6 为A11 线圈内部不同位置发生24 匝金属性短路时的If。

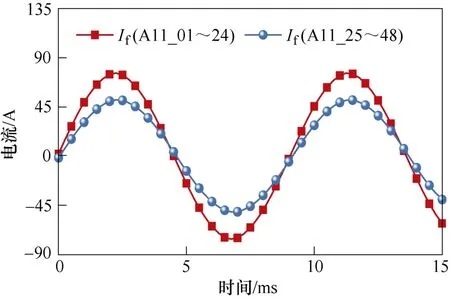
图6 不同位置发生24 匝金属性短路时的IfFig.6 If of 24 turns metallic short-circuit at different positions

由图6 可知，槽口24 匝金属性短路时的If幅值远大于槽底24 匝金属性短路时的If幅值。这是由于槽内相同匝数不同位置线圈的电感沿槽深方向依次增大造成的。对比分析图4c～图4f 和图6 可知，在Nf和Rf相同的前提下，槽口故障的If大于槽底故障的If；槽口故障的VA和Tave小于槽底故障的VA和Tave，说明槽口故障对电机性能的影响大于槽底故障。可以看出，该APM 能够精确分析线圈内部不同位置ISF 对电机性能的影响。当APM 仿真模型完成建模后，对WSF 状态分析时，单次仿真计算需要10.8 s，而相同条件下FEM 的单次仿真计算需要4 323 s，APM 可以快速分析不同类型WSF。

APM 与FEM 的对比分析表明，该APM 不仅可以高效、精确地分析电机在不同类型WSF 下的相电压、支路电流、短路电流、平均转矩等电磁特性，还可以精细地分析槽内线圈不同位置的ISF 对电机性能的影响。利用APM 对槽内线圈不同位置ISF进行分析，发现在Nf和Rf相同的前提下，槽内不同位置ISF 下的短路电流和平均转矩不同，揭示了Nf和Rf作为故障程度判据的局限性。因此，为保证电机在槽内不同位置ISF 状态下仍能输出满足要求的转矩，其抑制短路电流的补偿策略也不相同。上述分析为PMSM 故障诊断及容错控制提供了依据。

3 实验验证

为了进一步验证所建立APM 的正确性和准确性，本文制造了2.1 节所述的PMSM 故障实验样机，并搭建了实验平台，如图7 所示。为了进行线圈内部不同位置的ISF 实验，将样机的每个线圈沿槽深方向横向分为四个线圈子单元，并将所有子单元的抽头引出，每个子单元的匝数为12 匝，如图7a 所示。实验平台由样机、转矩测量仪、磁粉制动器、工控机、驱动器、数字示波器、数字电桥、直流电源和短路电阻等构成。

图7 实验装置Fig.7 Experiment setup

首先对健康状态下的APM 进行实验验证。图8为额定工况下电机的线圈电压VA11、VA12及转矩的APM 结果与实验结果。

由图8 可知，VA11、VA12和转矩的APM 结果与实验结果的吻合程度较好，VA11的幅值明显小于VA12的幅值，最大误差分别为3.4 %、3.1 %和1.8 %。该误差是由于建模时忽略铁耗、磁路饱和、机械摩擦等引起的。实验结果验证了APM 不仅能精确计算电机健康状态下的电磁特性，还能分析不同位置的线圈对电机性能的贡献。

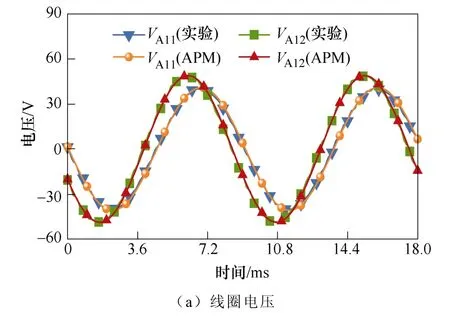
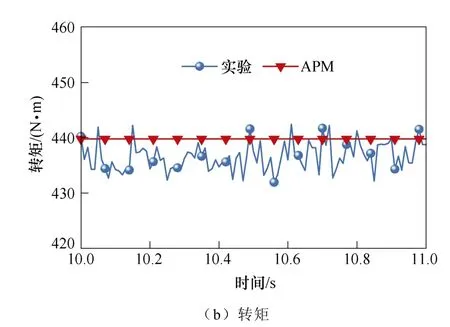
图8 额定工况下电机的线圈电压和转矩Fig.8 Coil voltage and torque of motor under rated condition

在进行电机WSF 状态实验测试时，将Rf连接至相应子单元的抽头之间。另外，为了保证实验设备的安全，Rf设置为2 Ω。图9 分别为额定工况时A12_01～48、A11_01～24、A11_25～48 和A34.48_C34.48 故障情况下If的APM 结果与实验结果。由图9 可知，If的APM 结果与实验结果的吻合程度较好，四种故障情况下最大误差分别为5.6 %、8.9 %、8.4 %及4.9 %。

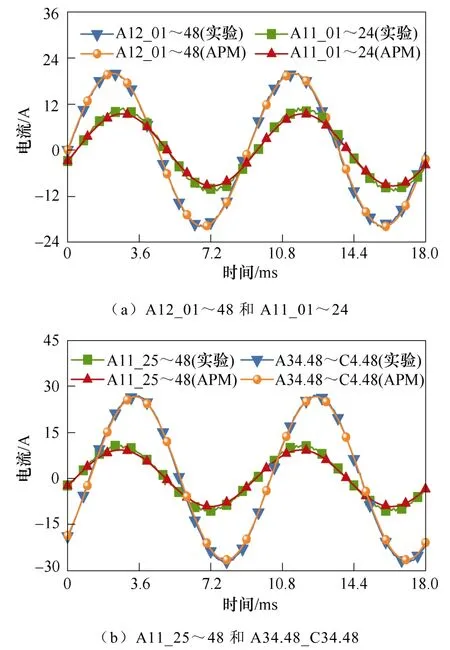
图9 不同故障类型下的IfFig.9 If under different fault types

图10 分别为额定工况时A12_01～48、A11_01～24、A11_25～48 和A34.48_C34.48 故障情况下故障支路电流IA1、IA3和IC3的APM 结果与实验结果。

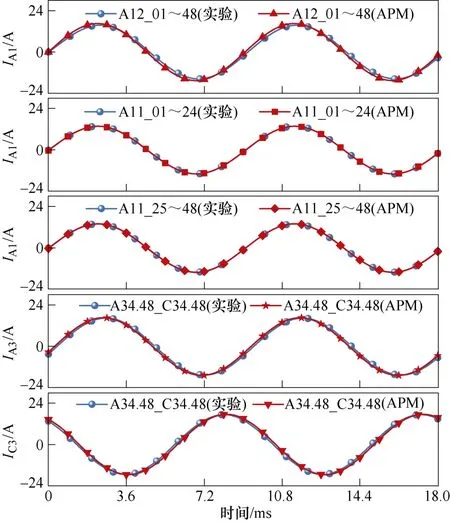
图10 不同故障类型下的故障支路电流Fig.10 Fault branch current under different fault types

由图10 可知，APM 结果与实验结果的吻合程度较好，A12_01～48、A11_01～24 和A11_25～48故障情况下IA1最大误差分别为 4.9 %、3.4 %及3.7 %。A34.48_C34.48 故障情况下IA3、IC3的最大误差分别为4.2 %、4.7 %。

图11 分别为25 %负载、100 %转速和25 %负载、50 %转速两种运行工况时A12_01～48 故障情况下If和IA1的APM 结果与实验结果。

由图11 可知，APM 结果与实验结果的吻合程度较好，25 %负载100 %转速与25 %负载50 %转速两种运行状态下，If的最大误差分别为6.2 %及4.6 %；IA1的最大误差分别为4.9 %及4.8 %。上述误差是由于建模时忽略铁耗、磁路饱和、短路电阻温升和机械摩擦引起的。实验结果验证了APM 在分析电机WSF 状态下电磁特性的正确性和准确性。实验结果验证了APM 不仅能精确计算电机WSF 状态下的电磁特性，还能分析线圈内部不同位置短路故障对电机性能的影响。

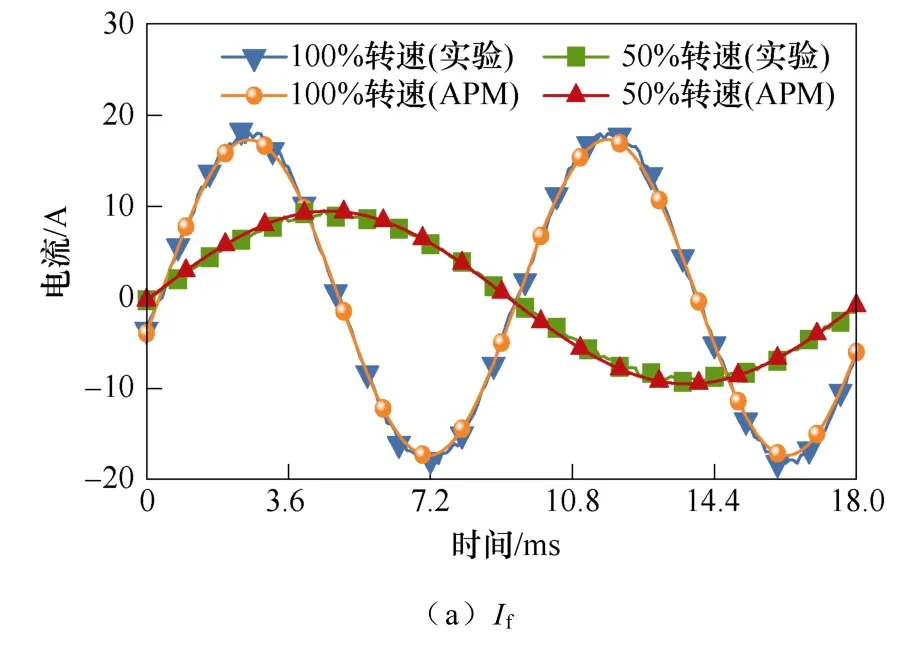
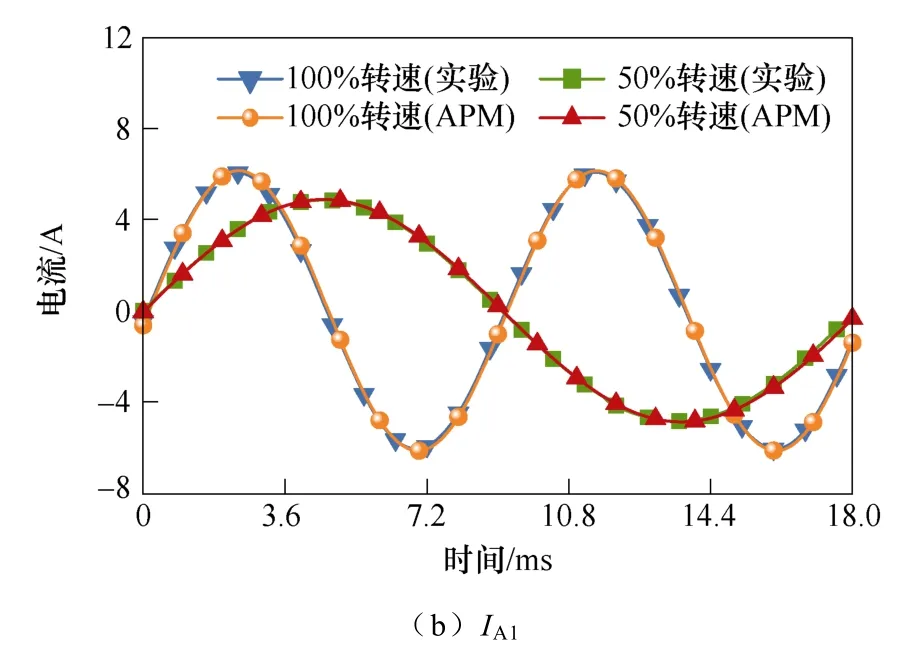
图11 两种运行工况下的If 和IA1Fig.11 If and torque under two operating conditions

4 结论

本文提出了一种基于线圈子单元的PMSM 健康与WSF 数学模型，并在Matlab/Simulink 中建立了其仿真模型和图形化界面。该模型考虑了绕组结构与短路空间位置的影响，可以分析健康状态时线圈对电机性能的贡献及线圈内部不同位置短路故障对电机性能的影响。通过将模型计算结果、有限元仿真结果和实验测量结果进行对比分析，验证了模型的正确性和准确性，并得到以下结论：

1）APM 通过修改抽头编号及图形化界面中短路电阻模块的连接位置，可以方便、快捷地计算电机健康和不同类型定子绕组短路故障下的电压、电流、转矩等电磁特性。

2）APM 可以精细地分析PMSM 健康状态时不同工况下线圈对电机性能的贡献。研究发现，PMSM绕组内不同位置的线圈对电机性能的贡献不同。

3）APM 在不改变内部结构的前提下，可以高效、准确、精细地分析ISF、相间短路故障等不同类型的WSF 下的电机性能。

4）APM 可以分析同一槽相同短路匝数槽口处短路故障与槽底处短路故障对电机性能的影响。研究发现，当短路匝数和短路电阻都相同时，PMSM 槽内线圈不同位置的短路故障对电机性能影响不同。

所提出的数学模型可为PMSM 的设计、故障诊断和容错控制奠定重要基础。