下行链路MUs-MISO系统URLLC的求和传输率最大化波束形成优化研究
曾陈萍,石荞语,叶长青
(1.西昌学院信息技术学院,四川 西昌 615000;2.四川省气候中心,四川 成都 610072)
0 引言
5G无线通信系统的一个重要特征是能够提供极高可靠性的无线通信,因此也被称为超可靠低时延通信(ultra-reliable low latency communication,URLLC)[1-3]。根据3GPP(3rd generation partnership project)[4],32字节的URLLC数据包典型可靠性定义为1 ms延迟内达到99.999%。与依赖足够长码字Shannon容量的传统通信不同,由于延迟限制,URLLC依赖短数据包传输[5]。正如Polyanskiy等[6]的研究,依靠短数据包无线通信系统的传输速率是关于系统带宽、译码错误概率和传输数据包长的复杂函数并严格小于Shannon容量表达,这也使得多天线传输中的波束成形设计是一个非凸问题并具有高度的计算复杂度。
目前,关于URLLC中波束形成设计优化的文献仍然较少,Sun等[7]、Nasir[8]、Nasi等[9]、Ren等[10]考虑了短数据包传输下的资源分配问题。具体来说,Sun等[7]考虑了在天线配置、带宽和功率分配的延迟和可靠性约束下最大化能效问题;Nasir[8]提出了一种改进的路径追踪算法,通过信道色散在中高信噪比(signal-to-interference-plus-noise ratio,SINR)下进行近似,考虑了在传输数据包长和总功率约束下最大化最小多用户译码错误概率问题;Nasi等[9]也通过函数近似求上下界的方式,在满足相同约束的条件下考虑了最大化最小传输速率问题;在NOMA(non-orthgonal multiple access)和OMA(orthgonal multiple access)系统中,联合优化功率和数据包长以最小化单用户的译码错误概率问题也在Ren等[10]的研究中进行了考虑。但是,在精确URLLC传输率公式下系统的求和速率最大化问题都没有在上述文献中体现。
在上述背景下,本文关注下行链路多用户(multi-users,MUs)多输入单输出(multiple-input single-output,MISO)系统的URLLC。以最大化所有用户设备(users equipments,UEs)的求和传输率为目标,考虑了MISO系统的波束形成设计优化问题。由于短数据包传输下传输速率表达式的复杂性,上述问题是高度非凸的,很难直接求解。为此,本文提出了一种计算高效的逐次凸近似(successive convex approximation,SCA)迭代算法来获得原问题的次优解。在不同发射总功率、天线数、传输带宽和传输时间下,通过数值仿真分析了所提算法的性能,结果表明,在预设的参数范围内,该算法得到的URLLC传输速率和Shannon传输速率较接近。
1 系统模型和优化问题公式
1.1 信号传输模型
在本节中,考虑一个下行链路MUs-MISO系统的URLLC,在该系统中基站(base station,BS)配备N个传输天线并服务于K个单天线UEs,所有UEs由索引k表示,其中k∈К={1,…,K}。hk∈ℂN×1表示由BS到第k个UEs之间的信道。在本文中,假设BS端完全已知hk的信道状态信息(channel state information,CSI)。在BS处采用线性预编码,wk∈ℂN×1表示针对用户k的传输编码向量。BS处的复基带传输信号可以表示为,其中,sk表示发送给第k个用户的信息符号,sk~CN(0,1),∀k∈К,且Pmax为BS处最大传输功率,有
由于URLLC在具体应用中的要求,采用短数据包进行数据传输,而且端对端的时延要小于1 ms[4],该时延严格小于信道的相干时间。为了便于分析,认为系统总传输带宽为B,单位带宽的噪声功率谱密度为δ2,系统的传输时间为t并严格小于信道相干时间。因此,在传输时间t内,认为信道响应hk满足准静态衰落而且是一个确定量。
在下行链路中,通过BS-用户信道,用户k接收到的信号由以式(1)给出:
式中:nk表示用户k处的加性高斯白噪声;nk~CN(0,),∀k∈К。由于单位带宽的噪声功率谱密度为δ2,那么σ2k=δ2B。
用户k的信噪比(signal-to-interference-plusnoise ratio,SINR)可表示如式(2)所示:
根据Polyanskiy等[6]的研究,在进行短数据包传输时,用户k的最大可达传输速率可以近似表示如式(3)所示:
式中:V(γk)=1-(1+γk)-2表示信道色散;Q-1(·)表示高斯Q函数的逆;Q(x)=εk表示用户k的块错误概率。
1.2 优化问题公式
在本文中,我们的目标通过优化设计BS端的波束形成实现多用户的求和传输率最大化。相应的优化问题可以表示为
式中:约束C1是BS处的总传输功率约束。由于优化问题P1非凸的目标函数,该问题的求解具有一定的计算复杂度,很难求出最优值。因此,需要对优化问题P1进行问题转换。
2 波束形成设计优化问题的转换和求解
2.1 优化问题的转换
首先,第k个用户接收到的期望信号表示为
式中:Hk=hkhHk∈ℂN×1;Wk=wkwHk∈ℂN×1。
此时,用户k的SINR和约束C1可以重新写为
随后,由于问题P1中存在非凸的目标函数,故采用凸函数之差的形式重写P1的目标函数,如式(8)所示。
将式(7)(8)(9)和(10)带入式(4)中,优化问题P1可以重新写为
虽然优化问题P2仍然是非凸的,但是上述变换有助于使用SCA迭代算法求得次优解。
2.2 优化问题的求解
为了解决问题P2中非凸约束C4,C5,C6,C8和非凸的目标函数,将采用SCA方法将其转化为凸函数之差的形式以获得其局部最优解。
首先,针对非凸的秩1约束C8,将采用式(12)[11]进行替换。
然后,采用基于SCA的迭代算法解决具有凸函数之差形式的约束。以约束C8为例,对其不等式的左侧项使用一阶泰勒级数展开,可以获得式(13)所示的凸上界:
式中:表示第n次迭代的可行解;λmax()表示最大特征值对应的特征向量。将(13)带入式(12)中,约束C8可以重新写为
另一方面,问题P2中非凸的目标函数,非凸约束C4,C5和C6也是以凸函数之差的形式存在。类似地,采用相同的方法求其凸上界。
问题P2中非凸的目标函数可以求得如式(15)所示的凸下界
然后,对P2中非凸约束C4,C5和C6采用类似的方法求其凸上界不等式,如式(16)所示。
最后,优化问题P3是一个标准的凸正定规划(semidefinite programming,SDP),可以采用CVX[12]进行求解。由于使用了SCA迭代算法,优化问题P3为原始优化问题P2提供了局部最优解。通过在第n次迭代中解决P3的优化问题来迭代更新可行解。所提出的基于SCA的算法如算法1所示。
3 算法设计
提出基于SCA迭代算法求解优化问题P3,具体如算法1所示。
算法1:基于SCA迭代算法求解优化问题P3。
初始化:设置初始化迭代指数n=0,设置最大迭代指数nmax=100,设置为合适的初始数值。
Step1:重复;
Step3:更新n=n+1;
Step4:直到P3的目标函数收敛或n=nmax。
优化问题P3一共有(KN)2+5K个优化变量,7K+1个仿射和凸约束。因此,每次迭代的算法复杂度约为{((KN)2+5K)(67K+1)}[13]。
4 数值结果和讨论
通过数值实例来评估所提出算法的性能。在MUs-MISO系统下,假设BS配备n=10传输天线并服务K=4 UEs,系统带宽B=1 MHz,系统的传输时间设置为t=0.1 ms,噪声的单位带宽功率谱密度δ2=-174 dBm/Hz,系统总传输功率约束Pmax=25 dBm,译码错误概率εk=10-9。为了便于分析,信道响应hk可以表示为其中,βk=-35.3-10αlog10(dk)[7]表示包含路径损耗大尺度信道增益,α表示路径衰落指数,并设置α=-4,dk是以米为单位的设备双方距离。表示小尺度下的Rayleigh衰落模型,满足~CN(0N,IN)。在本文中,采用直角坐标系来描述系统分布,BS所在的坐标位置分别是(0,0),UEs分布在以(200,10)为中心的半径为20的圆内。
采用如下所示的3种不同的基准来评估本文所提出算法的性能,分别是:
1)Shannon传输率(算法1):在该模型下,式(8)中αkA0=0。通过优化BS端的波束形成以最大化求和传输速率,该模型算法与算法1类似。
2)Shannon传输率(等功率传输):在该模型下,BS端的波束形成采用最大比传输(maximum ratio transmission,MRT)。定义
3)URLLC传输率(等功率传输):在该模型下,BS端的波束形成采用MRT。定义
图1给出了不同传输功率约束下系统求和传输率的变化曲线。和预期一致,系统求和传输率随着传输功率的增加而增加。同时,图1也给出了在等功率传输下系统的求和传输率曲线。图1的结果表明了文中所提算法1对比等功率传输下具有明显的优势。根据图1的结果,可以明显看出URLLC传输率与Shannon传输率的上界之差不会随着传输功率的增加而增加。
图2给出了传输时间t对系统求和传输率的影响曲线。和预期相同,URLLC的求和传输率随着传输时间的增加而增加,但是其增速随着传输时间的增加而变缓,这一点可以从URLLC传输率表达公式(3)看出。当传输时间t→∞时,Shannon传输率给出了URLLC传输率的上界。图2也表明低延时要求如何影响无线系统的频谱效率。因此,在进行系统设计时,根据服务质量(quality of service,QoS)要求,可以为设计目标选择合适的延时时间。同时,图2的结果也表明了算法1对比等功率传输下具有明显优势。

图2 在不同传输时间t下优化最大求和速率
图3给出了通过不同带宽B对系统求和传输率的影响曲线。和预期一样,图3中的求和传输率随着系统总带宽的增加而增加,这是因为系统提供了更多的资源。但是,URLLC传输率与Shannon传输率上界之差随着系统带宽B的增加而增加。同时,与图1和图2类似,图3也表明了算法1对比等功率传输下具有明显的优势。
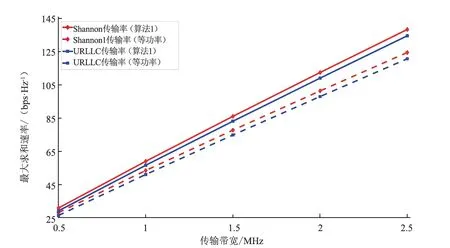
图3 在不同系统带宽B下优化最大求和速率
图4给出了不同天线数量N对系统求和传输率的影响曲线。可以看出,随着天线数量的增加,URLLC传输率和Shannon传输率之间的性能差距几乎固定不变。同时,与图1~2和图3类似,图4也表明了算法1对比等功率传输下具有明显的优势。
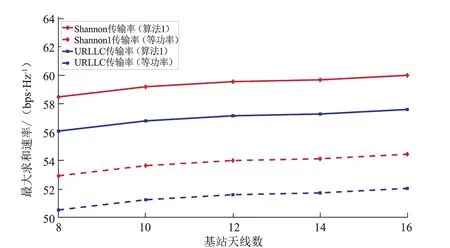
图4 在不同基站端天线数N下优化最大求和速率
5 结束语
本文考虑了下行链路MUs-MISO的URLLC系统。以最大化UEs的求和传输速率为目标,提出了波束形成设计的优化问题;采用SCA迭代算法求解原始非凸问题,实现了高效的URLLC网络。在不同发射总功率、天线数、传输带宽和传输时间下,通过数值仿真分析了所提算法的性能。数值结果表明,在预设的参数范围内,该算法得到的URLLC传输速率和Shannon传输速率较接近。

