双边钢箱钢-混组合梁斜拉桥抖振响应分析
陈建兵,陈星灿,王东伟,陈 鑫
(1.苏州科技大学土木工程学院,江苏 苏州 215011;2.中交一公局第二工程有限公司,江苏 苏州 215011)
对于大跨度桥梁来说,在紊流风场的作用下,桥梁结构均会产生抖振,抖振产生的位移可能使桥梁结构疲劳破坏,从而致使桥梁损毁,其带来的危害是致命的[1-2]。随着斜拉桥的发展,其在跨径、截面高度、材料等方面的改变,使整体桥梁结构越来越轻柔,进而产生的风致振动问题越来越严重,所以越来越多研究者专注于桥梁抖振研究[3]。
进行桥梁抖振研究时,通常使用现场实测和数值模拟等方法获得桥址处的脉动风速[4]。曾健[5]基于桥位处现场实测风速数据对山区悬索桥风致抖振响应以及风荷载长期作用于结构所引起的疲劳累积损伤进行分析,为山区同类型大跨度桥梁的抗风设计提供了参考。回城钰[6]基于实测风场数据对某斜拉桥进行抖振响应分析,并与规范风场荷载作用下的抖振响应进行了对比。研究表明,规范建议的风场荷载对斜拉桥抖振计算是偏保守的。诸多学者通过模拟的方法得到了脉动风速,并对实际例子进行了抖振时域分析[7-9]。在计算方法方面,曹映泓等[10]纠正了过去时程分析方法不能同时处理颇振和抖振的理论缺陷,在时域中统一了颤振和抖振的分析方法。韩万水等[11]通过斜拉桥实例验证,发现现有的抖振时域分析理论计算得到的抖振响应值与试验值存在一定的差距。董锐等[12]以桥梁结构为研究对象,对抖振响应的多目标等效静力风荷载计算方法进行研究,结果表明,该方法在抖振响应计算精度和荷载分布的合理性方面均表现良好。沈正峰等[13]对变槽宽比双主梁断面悬索桥抖振响应,提出考虑自激力和抖振力沿展向变化的频域和时域抖振计算方法。对于不同的主梁形式,雷永富等[14]通过风洞试验,对大跨度宽幅混合梁斜拉桥的抖振性能进行了研究。董锐等[15]对不同П型主梁断面的斜拉桥抖振性能进行研究,结果表明,不同外形主梁的抖振响应不同,通过改变外形可以改变П型主梁在任一自由度上的抖振性能。周奇等[16]对中央开槽箱梁断面斜拉桥进行了抖振数值分析,并建立了开槽断面斜拉桥的非定常随机抖振响应有限元频域数值分析方法。
虽然诸多学者对桥梁抖振进行了研究,但是对双边钢箱钢-混组合梁斜拉桥的抖振研究还未见报道。双边钢箱钢-混组合梁在满足截面抗弯和抗扭性能要求下,具有很小的结构自重,因此其跨越能力可以显著增强。基于此,笔者以沾临黄河特大桥这座双边钢箱钢-混组合梁斜拉桥为背景,通过模拟得到桥址处的脉动风速时程,对桥梁进行抖振时域分析,得到桥梁的抖振响应;使用控制变量法,改变风参数,得到了不同风参数下的桥梁抖振响应值,并与初始条件下的桥梁抖振响应值进行比较,给出风参数对双边钢箱钢-混组合梁斜拉桥抖振响应影响的规律,为今后该类型斜拉桥设计提供了参考。
1 抖振时域计算理论
1.1 脉动风场的数值模拟
在国内外的研究中,通常采用谐波合成法和线性滤波法对桥梁风场的脉动风时程进行模拟。笔者选用谐波合成法[17]来模拟脉动风场,谐波合成法通过对功率谱密度函数进行频域上的分解,将脉动风这一随机过程离散为一系列三角函数的叠加来实现。其优点为算法严密、计算准确、输出稳定,但是其缺点也较为明显,因为需要庞大的矩阵运算对功率谱密度函数进行频域上的分解,导致需要较长的运算时间,所以谐波合成法需要较高配制的计算设备。
将斜拉桥的三维脉动风场的各个分量简化为一个具有一维n变量、零均值的平稳高斯随机过程{fj(t)}(j=1,2,…,n),其互功率谱密度函数矩阵为
(1)

自相关函数矩阵可表示为
(2)
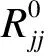
根据平稳随机过程的性质可得如下关系:
j=1,2,…,n.
(3)
j≠k.
(4)
(5)
由Wiener-Khintchine关系得式(1)和式(2)存在如下关系:
j,k=1,2,…,n.
(6)
将S0(ω)进行Cholesky分解:
S0(ω)=H(ω)HT*(ω).
(7)
其中,
(8)
式中:HT*(ω)为H(ω)的共轭转置。
一维n变量、零均值平稳随机过程fj(t),可运用式(9)进行模拟:
cos[ωmlt-θjm(ωml)+φml],j=1,2,…,n.
(9)
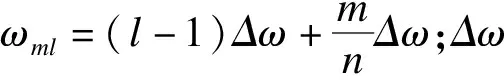
1.2 脉动风荷载的时域化
要进行抖振时域分析,首先就要对模拟得到的脉动风荷载进行时域化处理。脉动风荷载时域化的目的是建立脉动风荷载随时间变化的曲线关系。时域化的力学模型分为两种:一是基于准定常条件假定的抖振力模型;二是进行气动导纳修正的抖振力模型。
不考虑气动自激力的Davenport抖振力模型,即基于准定常条件假定的抖振力力学模型,其作用在桥梁主梁单位长度上的数学表达式为
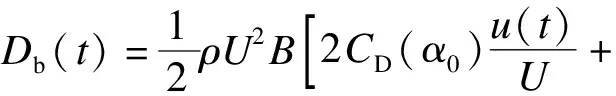
(10)
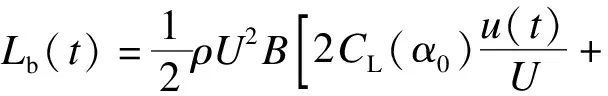
(11)
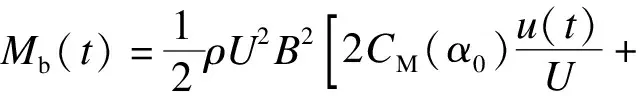
(12)
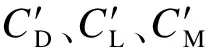
对于进行气动导纳修正的抖振力模型,其作用在桥梁主梁单位长度上的抖振力为
(13)
(14)
(15)
式中:χDu、χDw、χLu、χLw、χMu、χMw为Davenport气动导纳函数。
2 有限元模型建立
2.1 工程概况
沾临黄河特大桥是一座双边钢箱钢-混组合梁斜拉桥,跨径布置如图1所示。主梁采用双边钢箱钢-混组合梁,桥面宽34 m,含检修道宽38 m,主桥桥面板采用UHPC高性能混凝土板(见图2)。桥塔采用门型钢筋混凝土塔,主桥采用塔墩固结、塔梁分离的半漂浮体系,主梁与桥塔下横梁间设置支座;斜拉索呈扇形分布,斜拉索塔上索距为2.5 m,梁上索距为12 m。
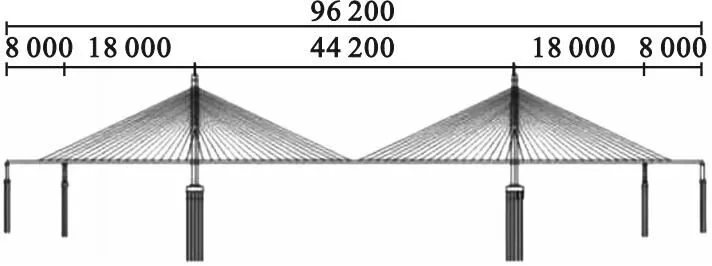
图1 斜拉桥总体布置图
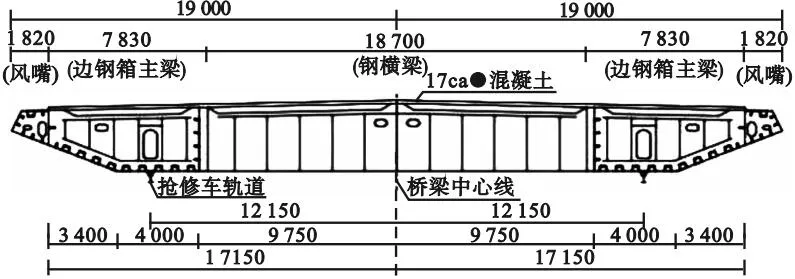
图2 主梁标准断面图
2.2 有限元模型
考虑到本桥扭转刚度较大,笔者使用ANSYS建立鱼骨式有限元模型,即使用单主梁模型来模拟桥面系。主梁、主塔及主墩单元采用Beam188单元,其中横隔梁采用刚度和质量一致的等代方法,以实参数的形式赋予主梁单元,斜拉索采用Link10单元,全桥模型如图3所示,梁节段模型如图4所示。全桥模型共有493个单元,其中主梁243个单元,主塔106个单元,斜拉索144个单元。主要振型频率见表1,一阶振型如图5所示。
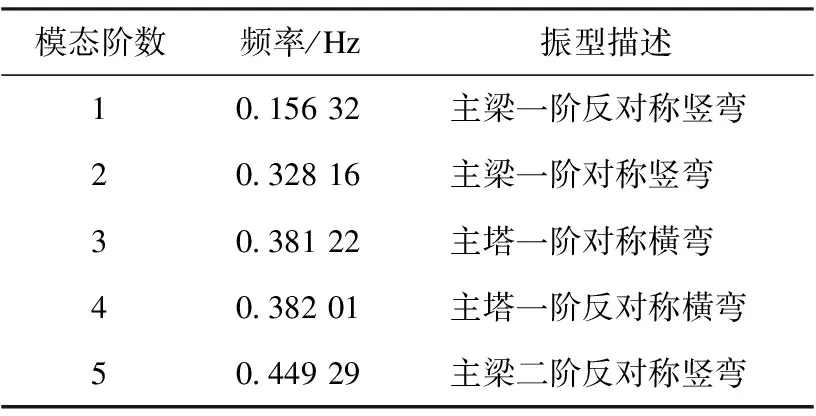
表1 主要自振频率表

图3 有限元模型
图4 梁节段模型

图5 一阶振型
2.3 典型主梁截面三分力系数计算
笔者使用流体软件FLUENT进行三分力的数值模拟计算[18]。计算中采用k-omega湍流模型,湍流强度取5%,湍流黏性系数取10,入口流速取28 m/s,上下边界设置为自由滑移壁面(symmetry),主梁断面采用无滑移壁面(wall)。模拟的主梁风速分布如图6所示,计算得到不同风攻角对应的的三分力系数如图7所示。由图7可见,主梁阻力系数呈现对称规律,随着风攻角绝对值的增大而增大,由于风攻角在0°时,迎风面积最小,阻力系数在0°攻角时达到最小。升力系数随风攻角的增大而增大,扭矩系数与其他两个系数相比变化较小。
图6 主梁风速分布
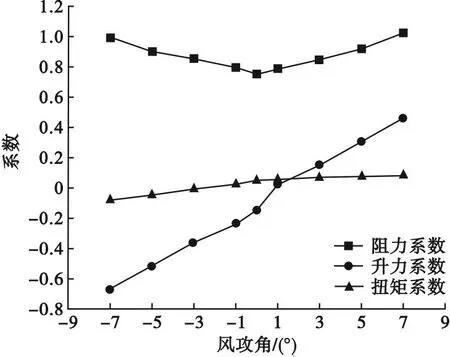
图7 主梁三分力系数
2.4 脉动风荷载模型
通过MATLAB对沾临黄河特大桥的桥面风速场进行数值模拟时,桥面平均高程取45 m,桥面设计风速取28 m/s,模拟点间隔取8 m。将主梁沿桥纵向划分为120个风速点,风谱采用规范推荐谱[19],即横向风谱采用Kaimal风谱,竖向风谱采用L-P风谱,模拟风速时长取1 024 s,时间步长取0.25 s,共计4 096步,频距和频率等分数分别取0.001 Hz和1 024。中跨跨中处的水平脉动风速时程和竖向脉动风速时程如图8和图9所示。使用MATLAB对风速时程进行功率谱密度函数分析,以确保所得到的风速数据的准确性。将脉动风速功率谱与目标谱进行比较,结果显示模拟谱与目标谱吻合较好(见图10和图11),验证了笔者所建立模型的准确性。
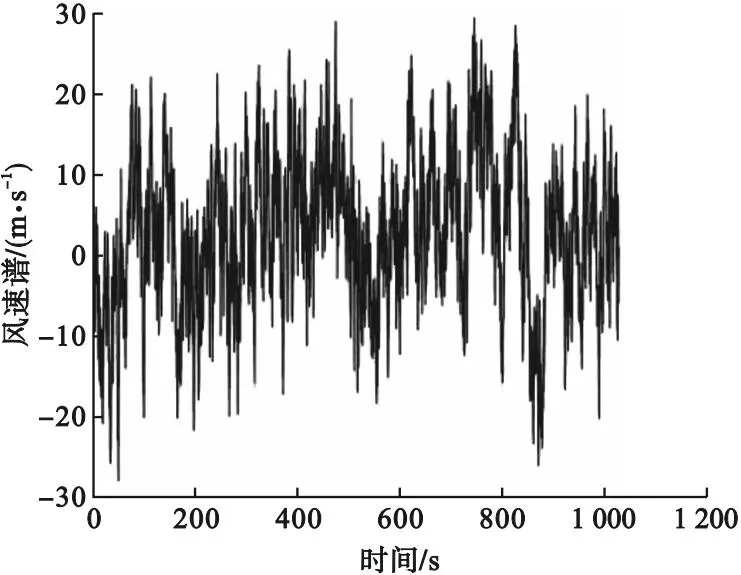
图8 跨中水平脉动风速时程
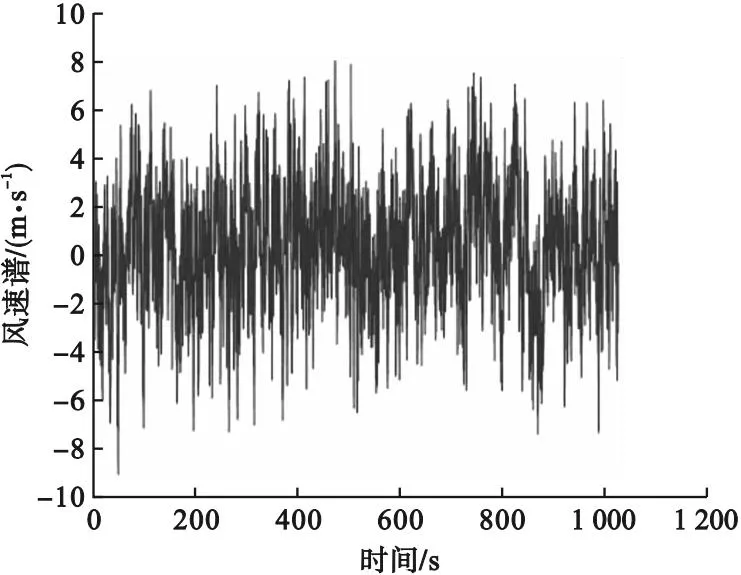
图9 跨中竖向脉动风速时程
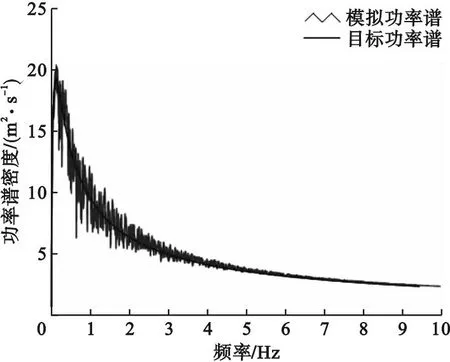
图10 水平脉动风模拟功率谱
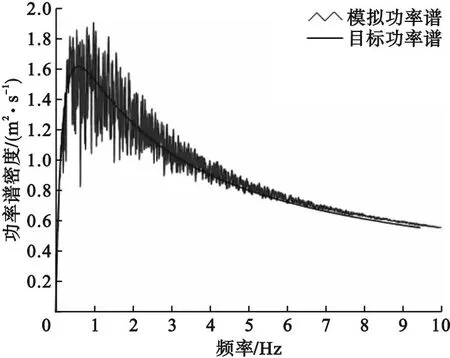
图11 竖向脉动风模拟功率谱
2.5 脉动力时程
时域化处理时,风速取设计基本风速为28 m/s,风攻角取0°,升力系数、阻力系数以及力矩系数分别为-0.148 6、0.752 4和0.046 1,一阶导数分别为0.089 0、-0.001 2和0.013 2。基于准定常条件假定的抖振力模型对脉动风速时程进行处理,得到结构单位长度的脉动力时程,中跨跨中处的阻力脉动时程、升力脉动时程及力矩脉动时程如图12所示。
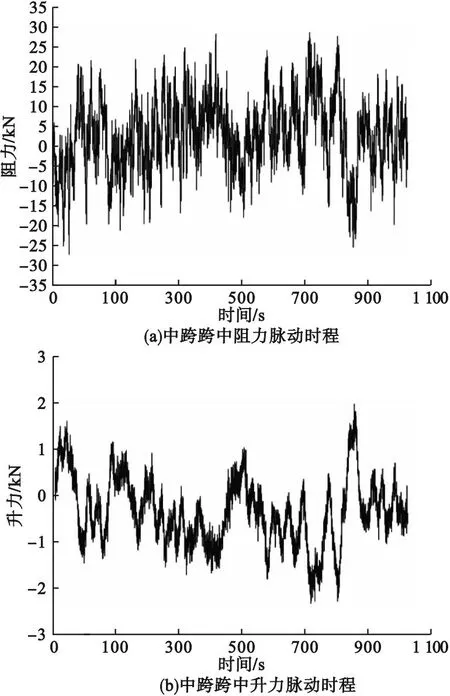
图12 跨中脉动时程
3 抖振时域分析
抖振时域分析是将转化成功的脉动力时程数据导入ANSYS中,施加到对应的位置上,然后进行瞬态模块处理。在瞬态分析中,步长取0.25 s,计算2 400个时间步,时间总长为10 min,桥梁阻尼采用瑞利阻尼。再通过ANSYS导出计算结果,即节点位移时程曲线,最后由Excel对数据进行处理,进而得到主梁各点抖振位移响应均方根值RMS,这样可以更加直观地看到沿主梁纵桥向的位移时程响应分布情况。
3.1 初始条件
气动导纳函数值取1,风攻角取0°,平均风速取设计基准风速28 m/s。沿主梁纵桥向的抖振竖向位移、横向位移以及扭转角的RMS分布情况如图13所示。根据以上抖振计算结果可知,忽略气动导纳的影响、风攻角为0°以及取设计基准风速情况下,脉动风产生的抖振对桥梁结构的影响较小,橫向、竖向位移及扭转角基本上和静风条件下的结果差异很小,可能是由于本桥梁结构刚度比较大,抖振力无法产生较大的作用。从计算得到的数据可得,跨中竖向抖振位移最大值为10.9 cm,跨中横桥向抖振位移最大值为0.37 cm,跨中扭转最大值为3.75×10-5rad。上述结果分别为相对应的抖振位移RMS值的278.7%、332.1%、361.1%。所以抖振响应的时程曲线能清楚地反映出结构各个位置处的最大位移响应,以便于找到桥梁结构最不利的位置,并采取相应的防范措施。
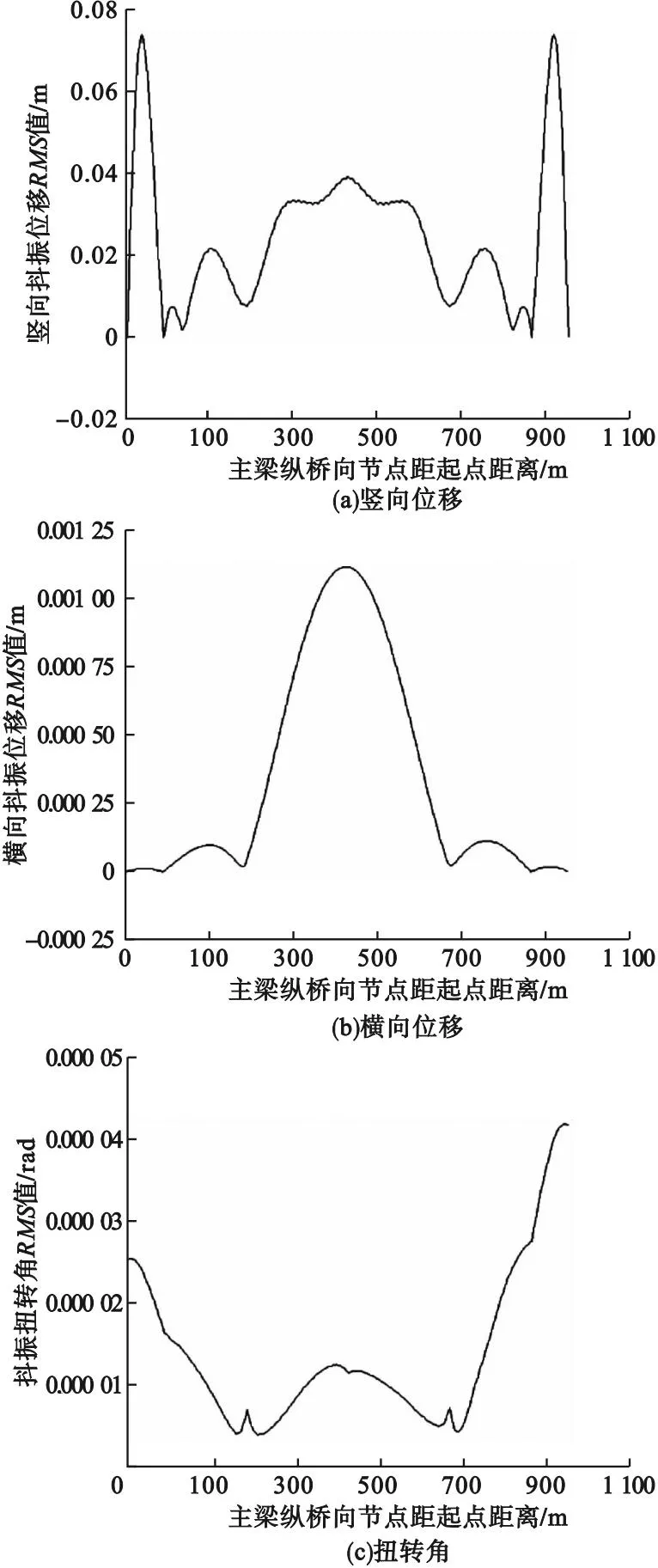
图13 主梁各节点抖振响应RMS值
3.2 风攻角
理论分析时一般都会选择0°风攻角这一理想条件进行桥梁结构抖振响应分析,但是在实际风场中,风是从众多方向吹来,从而导致风攻角不一定是理想条件下的0°。而不同的风攻角下截面有着不同的三分力系数,从基于准定常条件假定的抖振力模型可以看出,三分力系数的不同,导致桥梁的抖振力的不同。本节计算了沾临黄河特大桥风攻角取值分别为+7°、+5°、+3°、+1°、-1°、-3°、-5°、-7°时的抖振响应,并与0°时的抖振响应进行对比。不同风攻角下各节点的抖振响应RMS值如图14所示,主梁中跨跨中随风攻角变化的抖振位移响应值如图15所示。
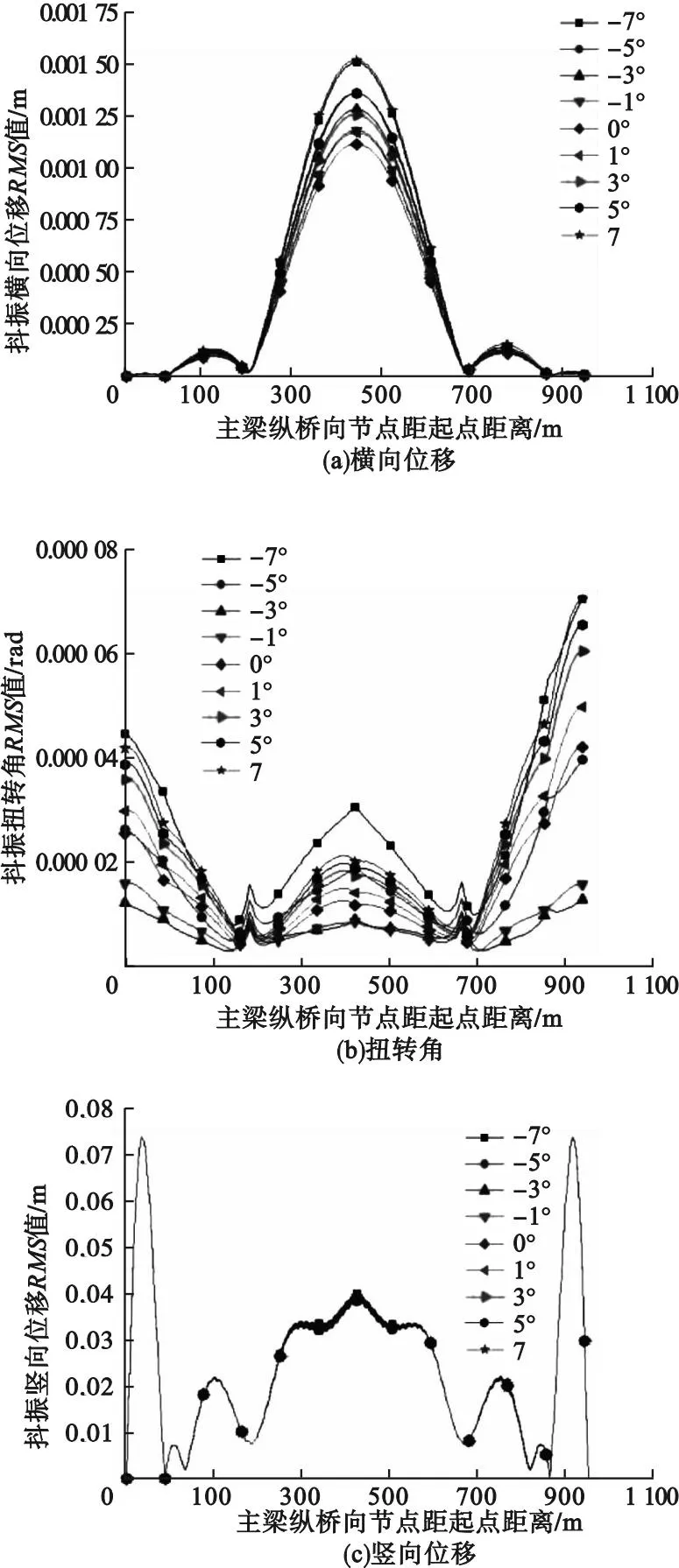
图14 不同风攻角抖振RMS值比较
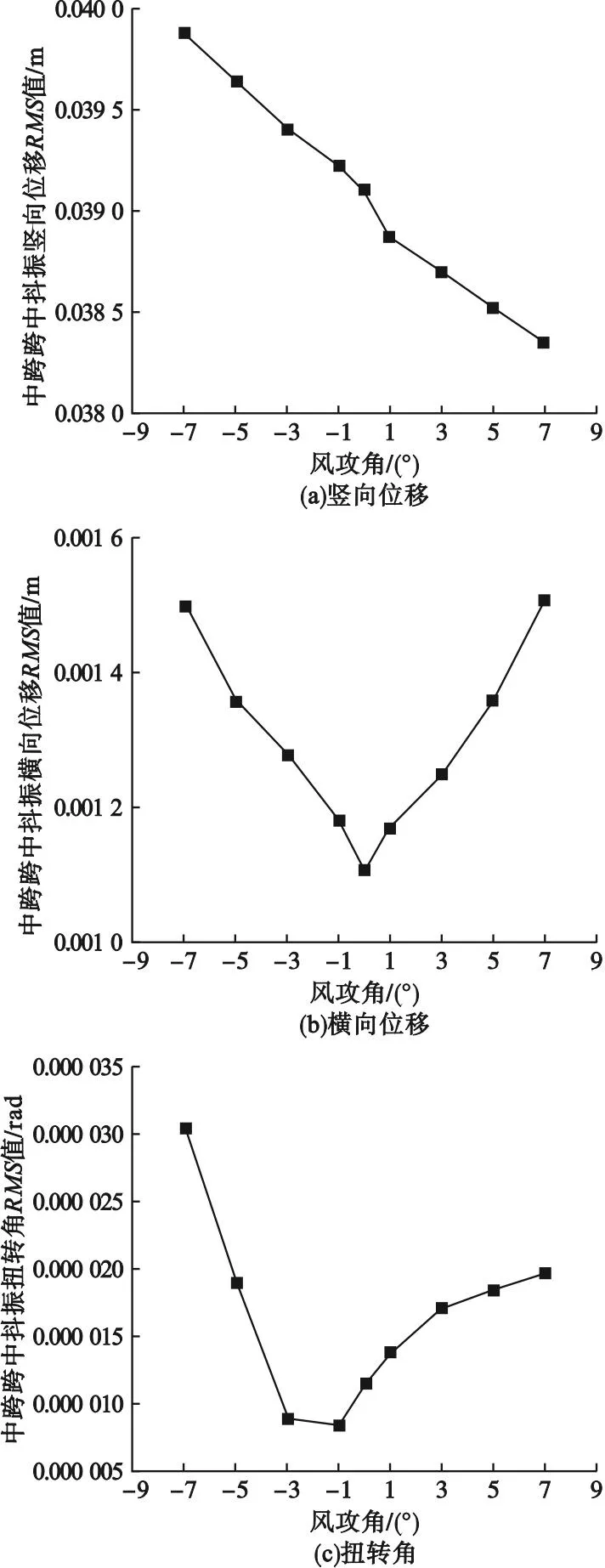
图15 中跨跨中抖振RMS值
从图14可以得出,对整体结构而言,风攻角越大,桥梁抖振响应越明显,且负风攻角的影响比正风攻角更大。在自重情况下,对于桥梁结构的抖振竖向位移及抖振扭转角而言,风攻角为负时的抖振响应比风攻角为正时的抖振响应更大;而对于抖振横向位移而言,正风攻角与负风攻角的影响值并无较大差距。从图15可知,抖振扭转角在-7°时最大,为0.000 031 rad,在-1°时最小,为0.000 009 rad,最大值为最小值的344.4%;抖振横向位移在7°时最大,为0.001 5 m,在0°时最小,为0.001 m,最大值为最小值的150%;抖振竖向位移在-7°时最大,为0.039 88 m,在7°时最小,为0.038 35 m,最大值为最小值的104%。因此,不能忽略风攻角对桥梁抖振的影响,在桥梁抗风设计中,可以按照来流风向出现不同角度的概率,取一个适当的风攻角进行计算,这样保守的设计可以让桥梁结构更安全合理。
3.3 气动导纳函数
在上文的计算中,忽略了气动导纳函数的影响,即气动导纳函数为1,但是在实际情况下,桥梁结构抖振响应受到风荷载的非定常特性的影响,进而影响着抖振响应的计算精度,所以计算过程中,三分力系数按0度风攻角取值,梁高处平均风速取设计基准风速,气动导纳函数采用Sears函数。
沿主梁方向上各节点考虑气动导纳与不考虑气动导纳两种情况下的抖振位移RMS值如图16所示。分析可知,忽略气动导纳函数的抖振位移响应值和内力响应值均大于考虑气动导纳函数修正后的抖振位移响应值和内力响应值。因为是在自重状态下的抖振响应,所以竖向的抖振响应基本上没有变化。而主梁跨中抖振横向位移响应RMS值减少了27.27%,扭转角RMS值减少了28.14%,橫桥向弯矩减少了36.17%,顺桥向弯矩减少了34.35%。由此可见,忽略气动导纳函数的影响,即气动导纳函数取1,从结构整体安全性角度讲,计算结果是偏保守的。因为桥梁结构抖振响应会受到气动导纳函数较大的影响,所以在需要对其抖振响应进行精确的分析时,就必须把气动导纳的影响考虑在内。因为Sears气动导纳函数是基于片条理论推导出的,所以在考虑气动导纳函数的影响时,为了得到比较准确的抖振响应值,必须通过相关的风洞气动导纳试验获得该结构准确的气动导纳函数。
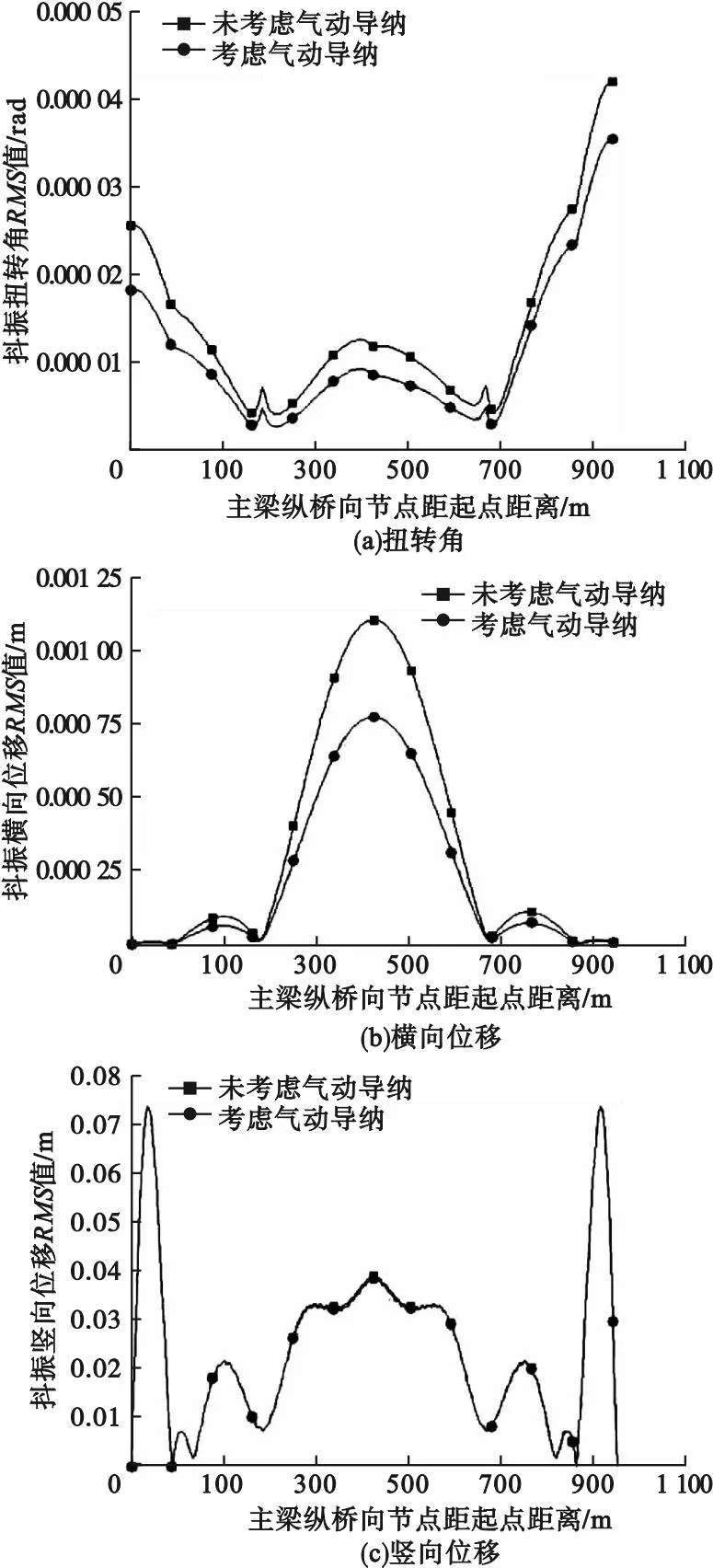
图16 气动导纳抖振RMS值比较
4 结 论
(1)对整体结构而言,风攻角越大,桥梁抖振响应越明显,且负风攻角的影响比正风攻角更大。随着平均风速的增大,沿主梁纵桥向方向各节点的抖振位移响应值也随之增大。
(2)气动导纳函数本身就是一个折减函数,忽略气动导纳函数的抖振位移响应值和内力响应值均大于考虑气动导纳函数修正后的桥梁抖振位移响应值和内力响应值。故以0°风攻角、设计基准风速、忽略气动导纳为条件进行桥梁设计是偏安全的。

