基于性能的新型装配式钢节点混凝土框架结构抗震设计

戎 贤,郝君临,张健新

(1.河北工业大学土木与交通学院,天津 300401;2.河北省土木工程技术研究中心,天津 300401)

随着我国建筑业的高质量发展,装配式混凝土框架结构由于具有绿色、高效和产业化等优势,有效提高和保证了建筑工程质量,从而在工程中得到了广泛应用。20世纪90年代,第一个关于装配式混凝土抗弯框架抗震性能的研究由美国国家标准和技术研究所提出[1],由此学者们开始大量研究并获得了众多研究成果。C.Li等[2]针对一种带有可更换耗能连接器的预制混凝土框架进行抗震性能研究,试验结果表明REDC-PCF滞回性能优越,可以实现理想的梁铰屈服机制;S.C.Girgin等[3]研究了预制框架的响应修正系数,并提出一种用于评估多层预制混凝土结构抗震性能的数值模型;L.Huang等[4]对后张自复位预制混凝土框架结构(SCPC)进行了基于性能的抗震设计及非线性时程分析,结果表明,与传统连接相比,该连接形式在承载能力、耗能能力和恢复能力方面均有显著的改善。我国对于装配式混凝土框架结构的研究起步较晚,近几年,国内对于装配式混凝土框架结构的研究通常集中在提出新型装配式节点连接形式[5-8]或使用新型材料[9-10]。然而,目前针对装配式混凝土框架结构的研究,较多围绕其节点和构件,对结构层面的研究较少。由于全尺寸低周往复加载试验与振动台试验的高成本和复杂性,或者无法保证有限元模型的准确性及可靠性,装配式混凝土框架结构的整体性能研究受到了限制。此外,虽然大部分装配式混凝土结构在施工现场安装时已经完成了装配,但连接节点仍需要在现场进行混凝土浇筑,这样的施工方式会增加施工的难度,并且延长施工时间,可能对结构的性能产生不利影响。

钢连接技术具有高效性和灵活性,但由于钢结构自身耐火性和耐腐性较差等因素,也限制了其应用。戎贤等[11-15]提出了一种新型装配式混凝土框架节点,该新型节点将钢结构梁柱节点连接方式的设计理念应用于混凝土结构中。笔者基于这种新型装配式混凝土框架节点建立了新型装配式钢节点混凝土组合框架结构(PCF)的有限元模型,并采用基于性能的抗震评估方法,进一步分析该节点在结构层面的抗震性能,研究表明,该新型节点在整体结构中表现出较好的抗震性能,特别是在延性及耗能方面,且PCF结构相较于RCF结构具有更强的抗倒塌能力。

1 基于性能的抗震设计方法

Perform-3D是一款三维建筑结构非线性分析软件,其提供的纤维截面建模在基于性能的抗震评估中得到了广泛应用[16-17]。笔者运用Perform-3D对现浇钢筋混凝土框架结构(RCF)与新型装配式钢节点混凝土框架结构(PCF)进行Pushover分析、弹塑性时程分析以及基于IDA方法的地震易损性分析,对比计算两种结构的超强系数及延性系数,得到罕遇地震下的层间最大位移角、楼层最大位移、楼层最大剪力和结构地震能量耗散等重要指标。基于IDA方法研究结构在不同地震强度下的抗震性能,计算抗倒塌安全储备系数CMR,定量评估结构的抗倒塌性。

2 新型装配式钢节点混凝土框架结构分析模型

2.1 新型装配式钢节点混凝土组合框架节点

该新型装配式混凝土框架节点的具体做法为在预制框架柱的梁柱连接处设置预埋钢节点,并在预制混凝土梁端部预埋一定长度的钢端头(见图1),借助钢结构的连接方法解决装配式混凝土结构连接薄弱等问题。为验证该节点的抗震性能,对其进行低周往复加载试验,试验结果表明,与现浇混凝土框架节点相比,该新型节点具有更高的承载能力、变形能力以及耗能能力[13]。

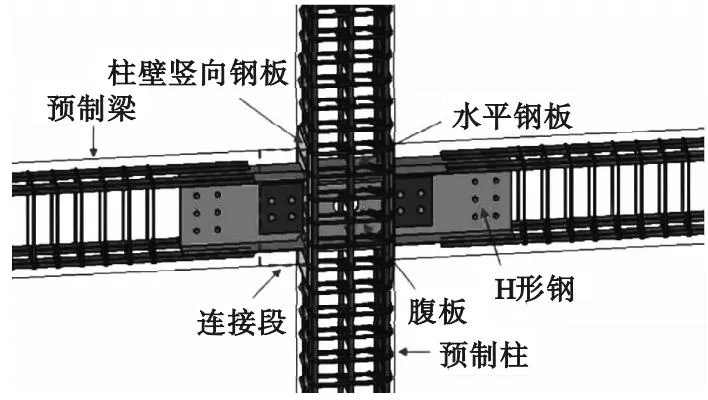
图1 装配式节点示意图

2.2 基于Perform-3D的有限元节点模拟及验证

笔者使用非线性分析软件Perform-3D对RCF结构及PCF结构进行梁柱纤维截面建模(见图2)。

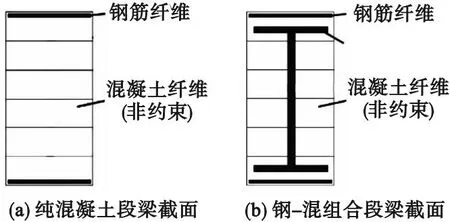
图2 梁柱非线性纤维模型

对于一般梁柱结构,塑性变形集中在端部,因此笔者选用图3的复合构件模式模拟框架梁和框架柱。钢筋及型钢的本构关系取值参照《混凝土结构设计规范》(GB50010—2010)的相关规定,在Perform-3D中采取双折线形式[18],混凝土的本构关系采用Mander模型[19],在软件中采用五折线骨架曲线进行简化。

图3 框架复合组件

为验证所建有限元模型的合理性,采用Perform-3D模拟课题组之前所做的节点试验[13],在柱顶施加恒定轴压力,在梁端施加往复荷载,模拟试验节点如图4所示,钢材力学性能指标见表1。

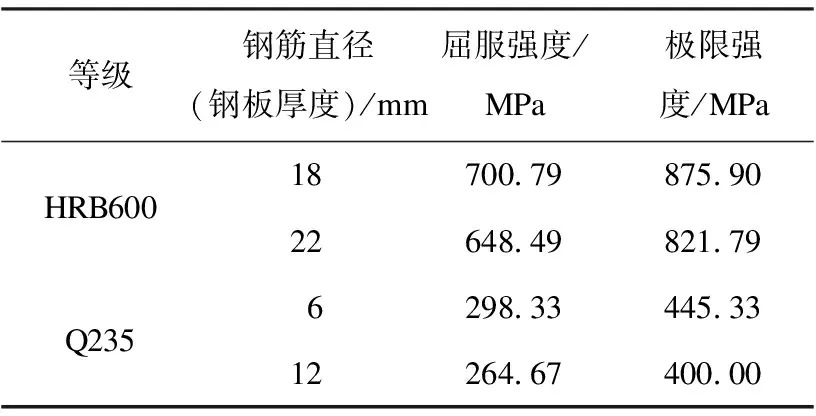
表1 节点低周往复试验参数

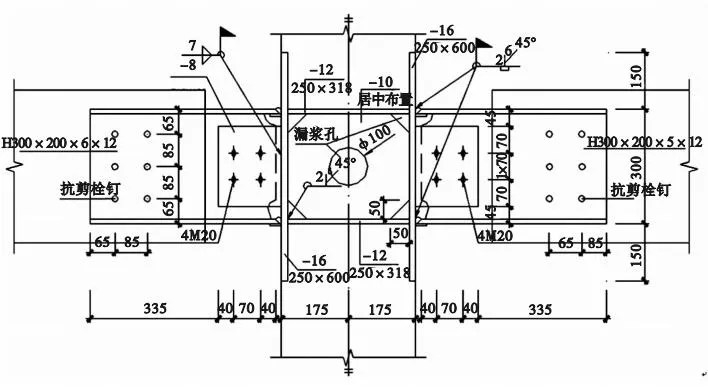
图4 节点示意图

将有限元软件Perform-3D及Abaqus模拟出的滞回曲线与试验数据进行对比,结果如图5所示。从图中可以看出,采用Perform-3D模拟出的滞回曲线与试验结果拟合效果较好,峰值承载力相当,可以证明采用上述纤维建模能够较好地模拟新型装配式钢节点。

图5 滞回曲线模拟与试验对比

2.3 结构分析模型

从图1可以看出,PCF结构节点处有一部分H型钢预埋在钢筋混凝土预制梁端头,还有一部分H型钢采用焊接和螺栓连接的方式与预制柱连接成整体,假设预埋H型钢长度为600 mm。RCF结构及PCF结构平、立面尺寸如图6所示。

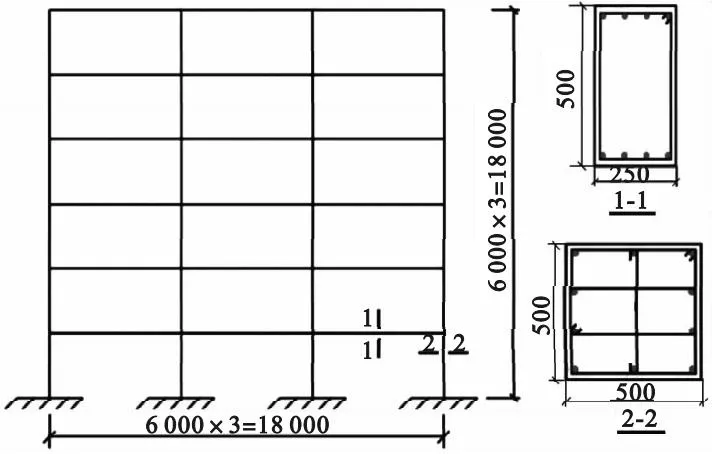
图6 结构的平立面示意图

两种模型结构的尺寸与材料参数相同,仅节点连接形式不同。模型抗震设防烈度为7度,设计基本加速度为0.1g,设计地震分组为第一组,场地类别为Ⅱ类,场地特征周期为0.35 s。模型结构平立面规则对称,共6层,结构层高为3 m,跨长为6 m。柱截面宽×高为500 mm×500 mm,梁截面宽×高为250 mm×500 mm。现浇混凝土板厚为170 mm,楼面恒荷载和活荷载分别为5 kPa和2 kPa;混凝土强度等级为C30,所有梁柱截面纵向受力钢筋及箍筋均为HRB400,型钢采用Q235钢材。

2.4 地震动选取

根据《建筑抗震设计规范》(GB 50011—2010)中的选波原则,选取两条天然地震波和1条人工模拟地震波,其中天然地震记录从PEER数据库中选取,包括FIRE STATION 22791记录的HECTOR MINE(T1)和USC STATION 90070记录的WHITTIER(T2),人工模拟地震波(R)则采用PBSD软件生成。图7给出了3条地震记录的加速度反应谱、平均反应谱及规范设计反应谱。

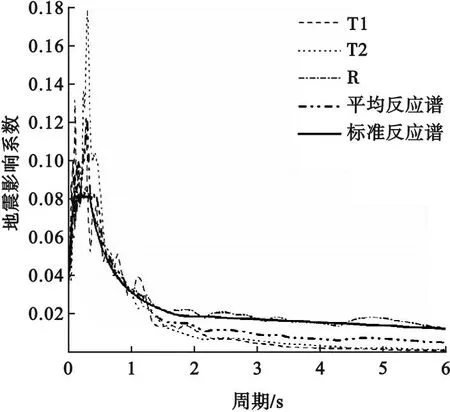
图7 地震波谱与反应谱对比

3 Pushover分析

Pushover分析方法是一种以结构的侧向位移作为整体抗震性能的结构抗震性能评估方法。在Pushover分析中,不同的侧向力分布模式可能会产生不同的Pushover曲线[20],因此笔者运用Perform-3D对RCF结构和PCF结构进行倒三角分布SPO1和均匀分布SPO2两种侧向力分布模式下的Y向分析,分别得到RCF结构和PCF结构在SPO1和SPO2下的Pushover曲线(见图8)。从图中可以看出,在初始弹性阶段,两种侧向力分布模式下的能力曲线较为接近,其初始弹性刚度相对一致;当进入弹塑性阶段时,两种结构内力均增长缓慢而塑性位移快速发展。在整个推覆过程中,均匀荷载模式的能力曲线一直位于倒三角荷载模式的能力曲线之上,倒三角荷载模式对于结构的抗震性能评估相对保守。此外,由图8对比分析可知,在两种侧向力分布模式下,与RCF结构相比,PCF结构的极限承载力与顶点最大位移均显著提高。

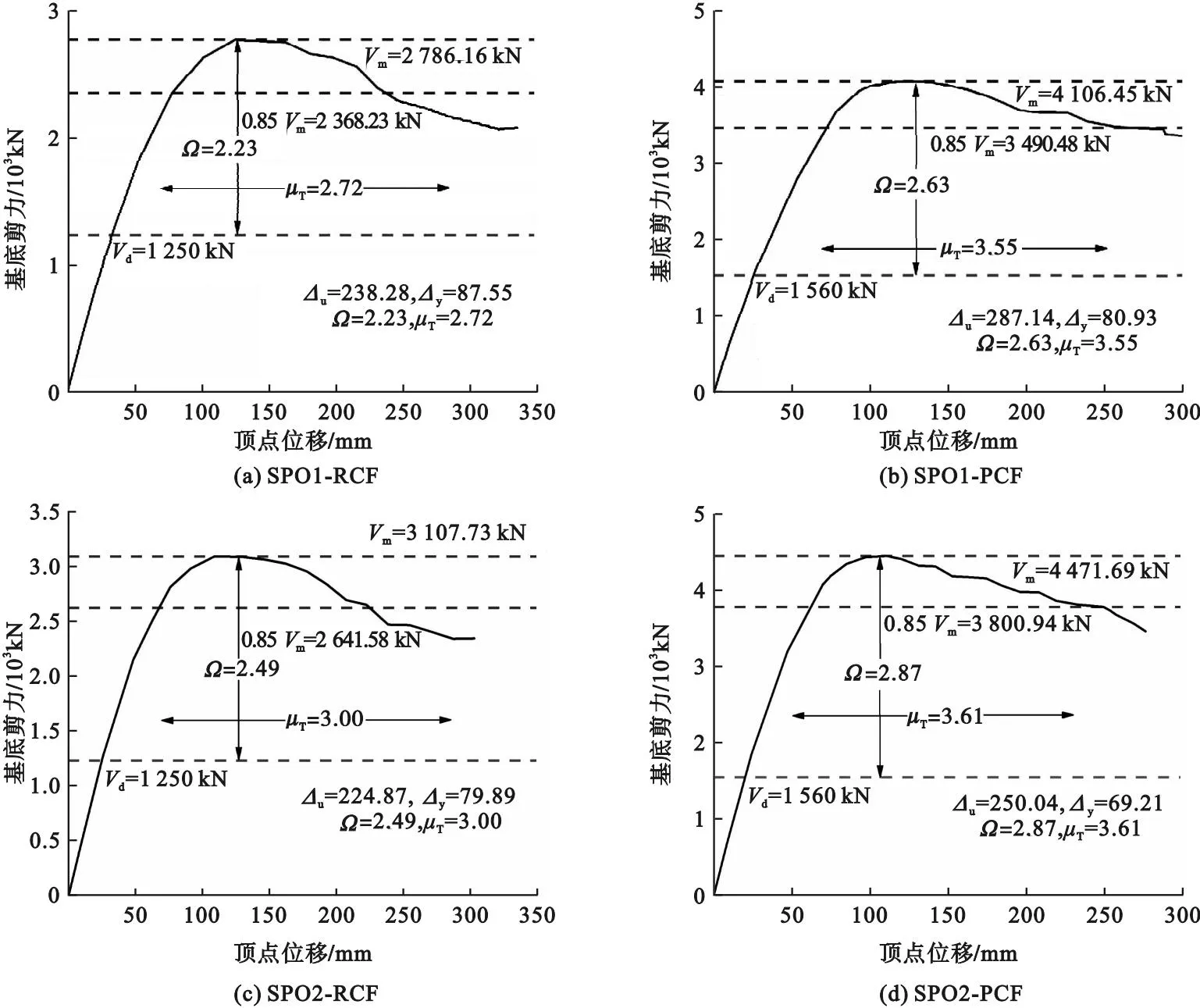
图8 两种结构的能力曲线

获得Pushover曲线后提取出相应的抗震性能参数:最大基底剪力Vm、设计基底剪力Vd、极限位移Δu和屈服位移Δy。屈服位移求解采用R.Park方法[21],即15%的抗剪承载力损失所对应的顶点位移值被视为极限位移。实际工程中,结构的设计抗震能力通常小于其实际的抗震能力,用超强系数表示,定义为结构实际的抗震能力与其设计地震力的比值;延性系数可以反映结构塑性变形和耗散能量的能力,定义为极限位移与屈服位移的比值。

在SPO1和SPO2作用下,RCF结构与PCF结构的平均超强系数分别为2.36和2.75,表明配置钢端头能够使结构在侧向荷载模式下获得更强的刚度和抗剪承载力。此外,RCF结构与PCF结构的平均延性系数为2.86和3.58,表明PCF结构中钢节点处水平-垂直钢板的设置能够有效提高位移延性系数,进而提升结构的抗震性能。

4 弹塑性时程分析

运用Perform-3D软件,以选择的3条地震波作为地震动输入,并将所选地震波峰值调整到规范要求7度罕遇地震的加速度峰值220 g,对RCF结构和PCF结构进行弹塑性时程分析,研究两种结构在地震输入下的能量分布。

RCF结构与PCF结构在三种地震波作用下得到的地震能量时程对比结果如图9所示。由图9(a)可知,RCF结构最大地震输入能为人工波作用下的8.259×108N·mm,PCF结构最大地震输入能为人工波作用下的7.458×108N·mm,人工波作用下的RCF结构最大地震输入能大于PCF结构;但在T1波和T2波的输入下,PCF结构的最大地震输入能大于RCF结构。由图9(b)可知,在地震初期,RCF结构与PCF结构的滞回耗能数值为0,阻尼耗能也很小,表明两种结构此时均无塑性变形,结构的地震输入能主要以动能和弹性应变能储存起来;随着地震能量的输入,RCF结构率先观察到滞回耗能现象,开始出现塑性变形;之后,地震输入能随总耗能的增加而迅速增加;随着地震波的输入,总耗能几乎不再增加,此时总耗能在地震输入能所占比例达到峰值,表明结构的耗能能力达到饱和,地震输入能绝大一部分被滞回耗能和阻尼耗能耗散。由图9(b)和图9(c)可知,PCF结构整体滞回耗能占地震总输入能的比例小于RCF结构,总耗能占总输入能的比例却大于RCF结构,说明PCF结构在罕遇地震作用下,塑性破坏小于RCF结构,整体耗能能力较优。

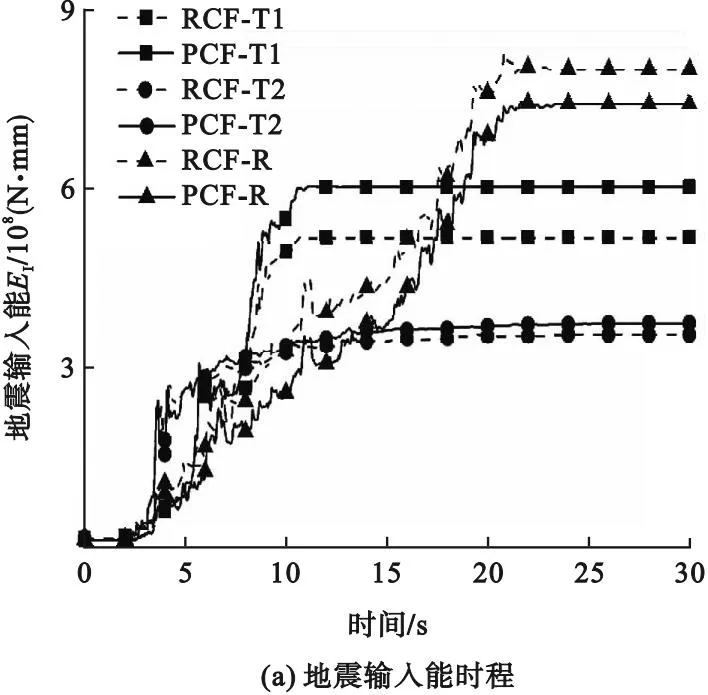
图9 不同地震波输入下地震能量时程对比

5 基于IDA方法的地震易损性分析

地震易损性分析可以基于IDA方法获得结构在不同强度地震作用下发生各种不同破坏状态的概率,该方法在基于性能的抗震评估中得到了普遍应用。笔者分别选用PGA和θmax分别作为IM和DM指标进行IDA分析,并采用抗倒塌安全储备系数CMR对结构的抗倒塌性能进行定量评估。

5.1 地震波选取

合理的地震易损性分析需要大量的强震记录,一般选取10～20条地震波记录就能满足一定的精度要求[22-23]。首次取PGA为0.2g,以0.2g为增量在0.2g～1g取值,在Perform-3D中对RCF结构与PCF结构进行地震易损性分析。地震波具体参数见表2。

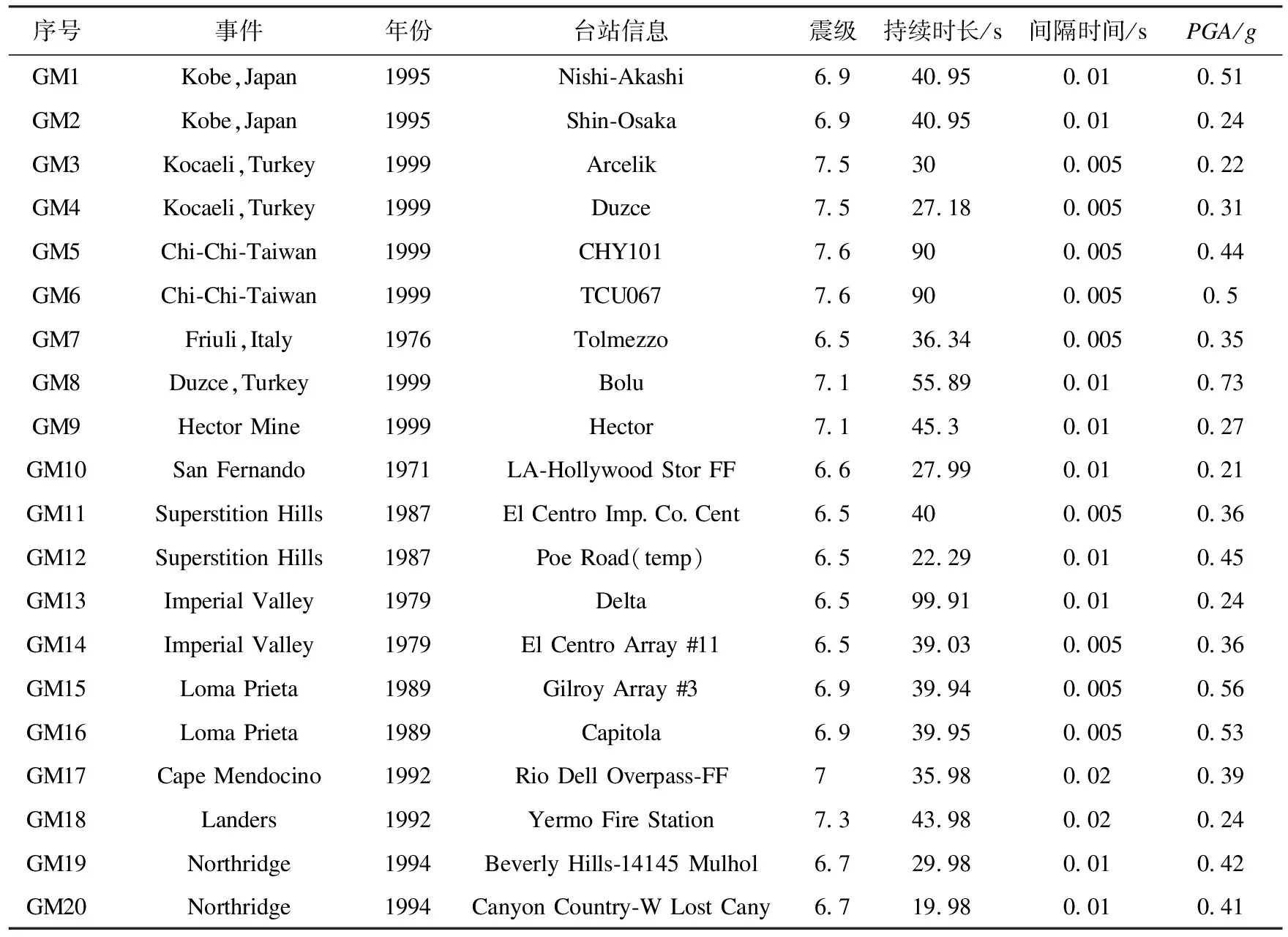
表2 地震动记录

5.2 增量动力分析

根据地震易损性分析步骤,对RCF结构和PCF结构进行多级强度水平下的非线性时程分析,并得到了两种结构的IDA曲线如图10所示。

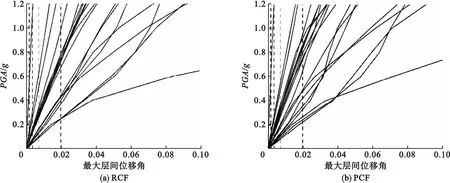
图10 IDA分析下结构最大层间位移角

从图中可以看出,RCF结构与PCF结构IDA曲线分布相似,先快速增加,然后逐渐趋于平缓。当PGA=0.2g时,RCF结构的平均最大层间位移角比PCF低0.015 6,这表明采用钢节点连接可以增强结构罕遇地震下的层间位移。当PGA为0.2g～0.8g时,RCF结构与PCF结构的最大层间位移角大致相同。随着PGA的增加,RCF结构与PCF结构的层间位移角平均值逐渐增大。当PGA=1.2g时,PCF结构的平均最大层间位移角比RCF结构高0.118 3,表明随着地震强度的增加,PCF结构表现出了良好的变形能力。

通过对PGA和最大层间位移角取对数,分别建立相应的坐标系,得到最终拟合结果如图11所示。对上述数据进行回归分析,得出RCF结构和PCF结构在不同地震强度下的地震需求线性回归方程。

图11 框架结构地震需求回归分析曲线

RCF结构:

lnθmax=-3.014 3+1.062 1 lnPGA.

(1)

PCF结构:

lnθmax=-3.144 2+1.032 2 lnPGA.

(2)

RCF结构和PCF结构的拟合系数R2分别为0.971 5和0.936 2,表明两种结构的线性回归模型拟合程度较好。

5.3 易损性曲线

地震易损性分析可以通过IDA分析获得易损性曲线来预测结构在不同等级地震作用下发生各级破坏的概率。结构抗力的极限状态取层间位移角为1/550、1/275、1/135和1/50作为结构抗震能力的界限值,分别表示正常使用LS1、修复后使用LS2、生命安全LS3和预防倒塌LS4,取值见表3。

表3 各破坏等级对应的层间位移角限值

RCF结构与PCF结构在最大层间位移角下的易损性曲线见图12。从图中可以看出,RCF结构的易损性高于PCF结构。两种结构在LS1和LS2状态下的易损性曲线几乎重合,说明新型装配式钢节点在LS1和LS2状态下对结构损伤几乎没有影响;随着结构地震动强度的增加,PCF结构的易损性优势逐渐显现,在LS3状态下,PCF结构的易损性程度略小于RCF结构,超越概率分别为95.86%和96.64%;在最终的LS4状态下,PCF结构较RCF结构显示出较大优势,超越概率分别为79.21%和88.42%。这表明采用新型装配式钢节点能够有效地减轻地震作用下结构的损伤,提升整体结构抵御强震的破坏概率,尤其在最终的结构倒塌极限状态阶段效果明显。

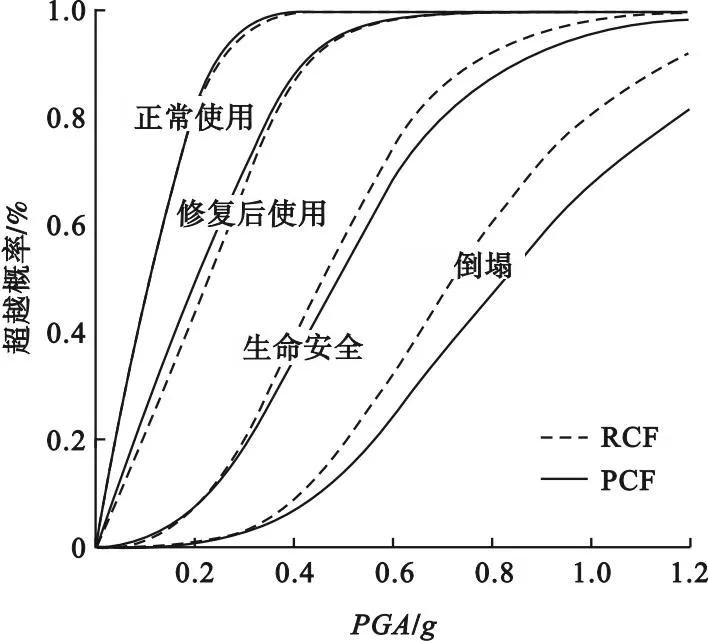
图12 基于IDA分析的结构最大层间位移角分布

5.4 抗倒塌储备系数

抗倒塌安全储备系数可以作为抗倒塌能力的量化指标,定义如下:

(3)

式中:IMCT为中值倒塌强度,定义为倒塌概率50%下地震易损性曲线上的PGA取值;IMMT为最大考虑地震的地震动强度,在我国可采用罕遇地震时的PGA。

抗倒塌安全储备系数越大,表明结构的抗倒塌能力越好,结构抗倒塌安全储备系数见表4。从表中可以看出,PCF结构抗倒塌安全储备系数大于RCF结构,表明新型钢节点可以显著提高结构的抗倒塌能力,具有更好的抗震性能。

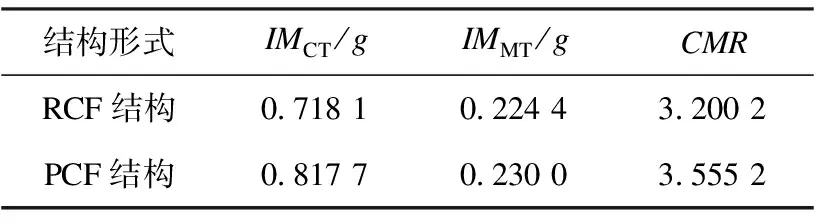
表4 结构抗倒塌安全储备系数

6 结 论

(1)由Pushover对比分析可知,倒三角分布模式对结构抗震性能的评估相对保守。此外,与普通现浇结构相比,新型装配式钢节点混凝土框架结构整体刚度较大,并且具有更高的承载能力与变形能力。

(2)由7度罕遇地震作用下非线性对比分析可知,新型装配式钢节点混凝土框架结构层间变形趋于均匀,与普通现浇结构相比具有较小的层间变形,延性较好,且能够承担更大的剪力。

(3)由不同地震波输入下地震能量时程对比分析可知,与普通现浇结构相比,新型装配式钢节点混凝土框架结构累积塑性损伤较小,整体耗能显著,且楼层滞回耗能占总滞回耗能比值较为均匀,没有发生能量集中现象,能够较好避免薄弱层失效。

(4)由基于IDA方法的结构易损性分析可知,普通现浇结构与新型装配式钢节点混凝土框架结构的最大层间位移角增幅均出现先增大后减小再增大的趋势;弹性阶段,两种结构的结构损伤几乎相似,但随地震强度增大,新型装配式钢节点混凝土框架结构能够有效减轻地震作用下结构损伤,提高结构抗倒塌概率。