车辆荷载作用下钢结构厂房微振动反应的数值模拟及TMD减振控制研究

李 兵,刘广蒴,裴晓丹,赵维新

(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168;2.中建三局第一建设工程有限责任公司,湖北 武汉 430040)

高新技术产业的飞速发展带动了各类电子设备工艺上的进步完善,精密仪器的加工精确度可达到纳米级。为保证精密仪器的正常运行,对于精密仪器的使用环境有着更高规格的要求[1-2]。微振动是影响精密设备及仪器正常运行的振动幅值较低的环境振动。精密仪器厂房周边车辆行驶引起的环境振动会降低精密仪器在使用时的精确度,严重时会影响精密仪器的使用寿命。目前对于结构的振动控制大多使用隔振支座、耗能构件以及隔振沟等方法,由于微振动的振动强度低、振动频带宽,上述方法难以达到理想的控制效果。

调谐质量阻尼器(Tuned Mass Damper,TMD)是一种被动控制装置,能够有效地控制交通环境激发的微振动。TMD的工作机理是当结构受到外部激励作用产生振动时,带动TMD系统一起振动,TMD系统相对运动产生的惯性力反作用到结构上,从而减小结构振动反应[3]。国外学者提出了TMD的最优设计方法,以TMD的控制效果为优化目标,求得TMD的质量、刚度和阻尼的最佳参数,进而减小结构的振动响应[4-11]。吕西林[12]、操礼行等[13]使用TMD对结构进行微振动控制,通过时程分析方法模拟了随机人行荷载激励。王明珠等[14]进行了现场振动测试,分析了TMD安装后对结构的减振效果。邓亚虹[15]、孙亮明等[16]通过模拟与现场实测,研究了车辆荷载激励下的振动控制以及车辆速度、振源距离等参数对振动控制效果影响。

TMD减振系统应用在楼盖结构上有良好的微振动控制效果,加设TMD减振系统后能满足人对于振动舒适度的要求。目前,国内外学者对于TMD微振动控制研究主要集中于人致振动响应与舒适度分析[17-18],而对于车辆荷载下的精密厂房TMD微振动控制研究较少。基于此,笔者对车辆荷载作用下钢结构厂房进行TMD微振动控制有限元分析,选取三种车辆荷载工况对钢结构厂房进行激励,在响应最大处和靠近激励处分别放置TMD,得到了不同TMD安装位置对结构减振的影响规律;同时分别改变TMD的质量比和刚度,得到了车辆荷载作用下控制结构微振动规律。

1 钢结构厂房微振动反应的数值模拟

1.1 有限元模型的验证

某精密设备厂房一层为钢框架结构,二层为双跨双坡的多跨刚架体系,中间柱与斜梁连接选择铰接。厂房长48.0 m,宽48.0 m,占地面积2 304 m2。厂房一层层高10 m,二层层高11.5 m,跨度8 m。钢结构厂房二楼放置了精密仪器,由于厂房周围有重型车辆行驶,导致设备产生振动,进而干扰了精密仪器的正常工作。表1给出了厂房部分构件参数,楼面局部平面布置见图1。

表1 厂房部分构件参数

笔者选取3种工况进行分析,其中工况一:场地两侧周边各有两辆满载重约50 t的卡车以40 km/h的速度行驶;工况二:场地两侧周边各有两辆满载重约50 t的卡车以60 km/h的速度行驶;工况三:场地两侧周边各有两辆满载重约50 t的卡车以60 km/h的速度与火车共同行驶。在不同工况下,分析车辆荷载作用下控制结构微振动规律。

根据上述工况,分别采用ABAQUS软件和Midas Gen软件建立两层钢结构厂房三维有限元模型(见图2)。对结构进行动力特性分析,得到了结构的前6阶振型和每个振型相对应的竖向振型参与质量,结果见表2。从表中可看出,Midas Gen软件所得的振型值略大于ABAQUS软件所得结果,两种软件所得的振型十分接近,验证了两种软件所建立钢结构厂房模型的正确性。

图2 有限元模型

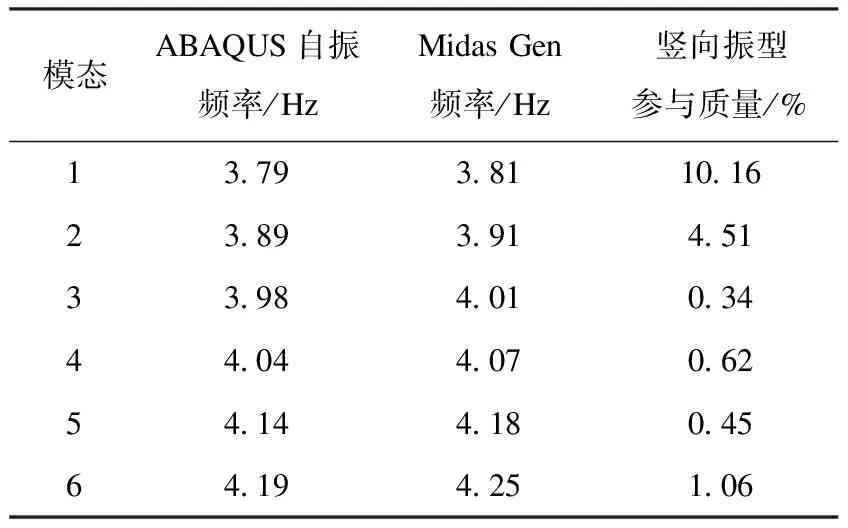
表2 结构前6阶振型频率

1.2 钢结构厂房的微振动反应分析

《电子工业仪器防微振工程技术规范》(GB51076—2015)规定,长路径激光设备、加工精度0.1 μm的超精密加工及检测装置在1～100 Hz内容许振动速度不应超过3 μm/s。在三种工况下,得到了距离车辆7.5 m固定点处的X、Y、Z三向加速度时程曲线,其中工况二下,加速度时程曲线如图3所示。将选取的三种工况下加速度曲线数值输入Midas Gen软件中,对结构进行激励,得到了三种工况下结构振动响应最大处的速度时程曲线(见图4)。

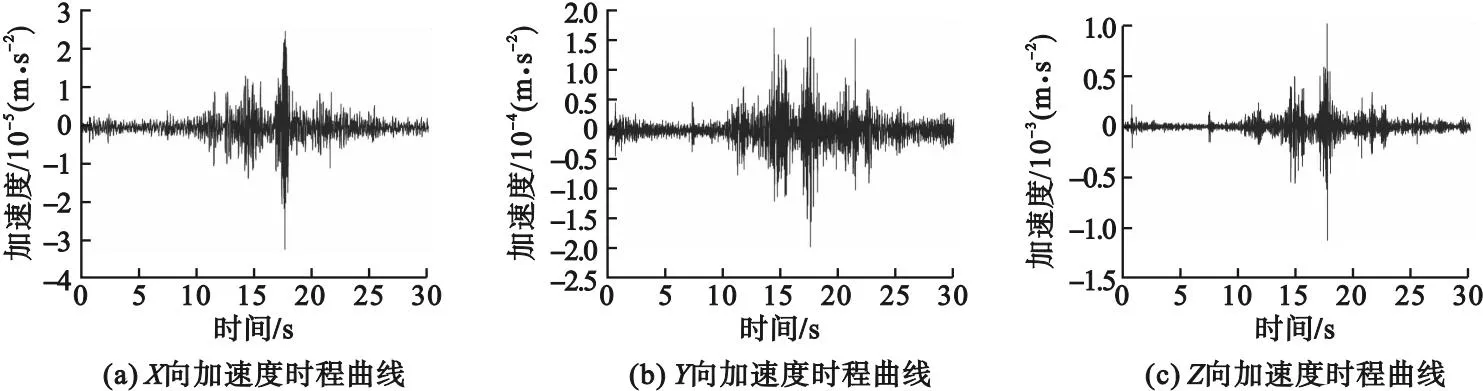
图3 不同方向加速度时程曲线

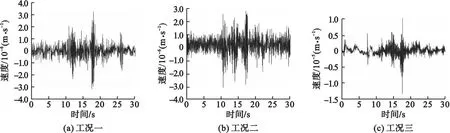
图4 三种工况下速度时程曲线

从图4可以看出,三种工况下最大振动速度均超过了精密仪器装置的容许速度限值3 μm/s。为了保证精密仪器的正常运行,减小车辆荷载激起的微振动,可重新选择钢结构厂房的梁柱部件,重新设计钢结构厂房,优化厂房使其达到规范要求以内。但此方法耗时耗力,明显不适用于已建钢结构厂房,故此选择在钢结构厂房上安装TMD控制微振动。可在现有的钢结构厂房结构上设置TMD,将TMD安装于钢结构厂房的二层楼板上,使最大振动速度降低至3 μm/s内,分析不同车辆荷载下的微振动变化规律。

2 TMD微振动的控制研究

2.1 TMD参数优化

2.1.1 TMD参数选择

TMD参数的选择很大程度上影响着结构的微振动控制效果,根据结构的模态质量、自振频率等参数可推导出TMD的最优参数。笔者采用J.P.D.Hartog提出的TMD的最优参数[19],TMD的质量比μ取值一般在0.01～0.05,TMD的弹簧刚度kTMD、阻尼cTMD的关系如下:

(1)

(2)

mTMD=μM.

(3)

kTMD=(2πfTMDηopt)2mTMD.

(4)

cTMD=4πfTMDηoptmTMDξopt.

(5)

式中:ηopt为TMD与结构模态的最优频率比;ξopt为TMD的最优阻尼比;mTMD为TMD的质量;μ为TMD与结构模态的质量比;M为主体结构振动模态质量;fTMD为控制频率;kTMD为TMD的弹簧刚度;cTMD为TMD的阻尼。

2.1.2 TMD参数确定

由表2可知,结构前6阶竖向自振频率,第一模态与第二模态的竖向振型参与质量远高于其他模态的竖向振型参与质量。未安装TMD时厂房结构的竖向振动由第一模态振型主导,且选取的荷载工况的激励频率接近于第一模态自振频率,故选取3.8 Hz作为控制频率,对应的振动模态质量为26 t。质量比μ取0.01、0.02、0.03、0.04、0.05,计算每一组质量比所对应的TMD的弹簧刚度与阻尼数值,结果见表3。

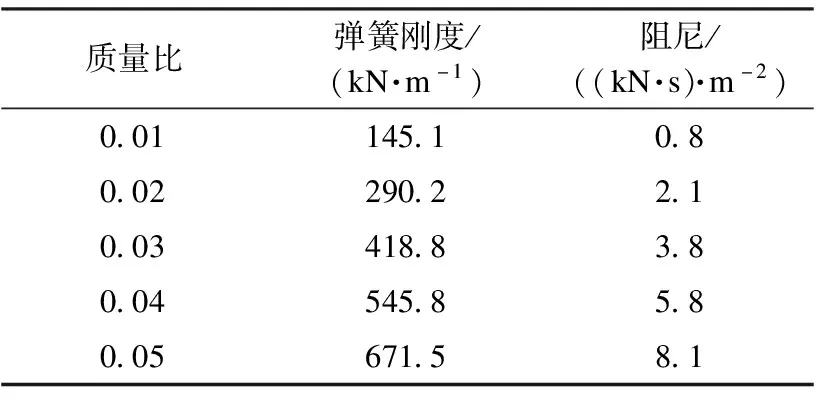
表3 TMD各项参数数值

2.2 TMD质量比

在Midas Gen软件中输入3种车辆荷载工况的振动波对钢结构厂房进行激励。3种工况的振动响应最大处均在钢结构厂房的2层楼板处,3种工况的竖向位移最大处距离十分接近,可近似看作一处(A1点),A1点位于1轴与D轴交汇处向左平移4.5 m,可将3种工况下,不同TMD安置处均选择为A1点。

改变TMD的质量比,分析在车辆荷载作用下TMD质量比变化对微振动控制效果的影响。依据表3中TMD参数,安装5次不同质量比的TMD于钢结构厂房楼板上A1点处。三种工况下平均速度减小幅度曲线如图5所示,与未安装TMD时进行对比分析,三种工况下速度时程曲线如图6所示。

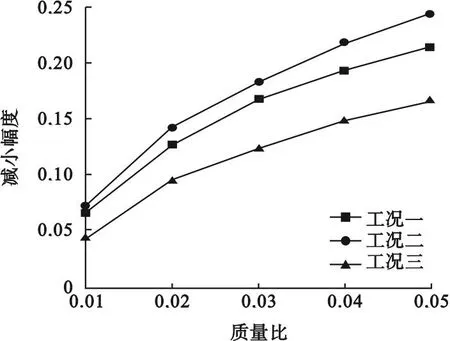
图5 A1处平均速度减小幅度曲线

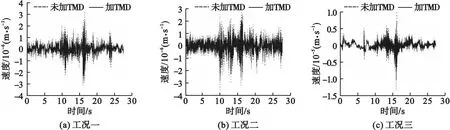
图6 A1处速度时程曲线

从图5和图6可以看出,楼板安装TMD后,随着TMD质量比的增大,振动速度逐渐减小,但振动速度降低幅度也逐步减小。当TMD质量比取0.05时,在工况三下,最大振动速度由13.33 μm/s下降至10.05 μm/s;在工况二下,最大振动速度由3.52 μm/s下降至2.81 μm/s;在工况一下,最大振动速度由3.24 μm/s下降至2.38 μm/s。三种工况下,最大振动速度和平均速度均有所降低。在TMD质量比取0.05时,工况一和工况二下,结构的最大振动速度均控制在3 μm/s以内,满足规范要求。

在3种不同工况下,TMD取不同质量比时,平均加速度减小幅度曲线如图7所示。

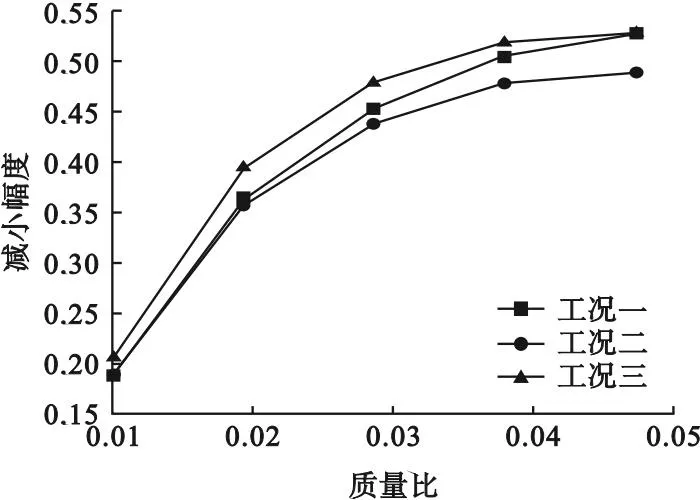
图7 A1处平均加速度减小幅度曲线

笔者选取质量比为0.05的TMD安置于A1点处,与未安装TMD时进行对比,得到加速度时程曲线如图8所示。

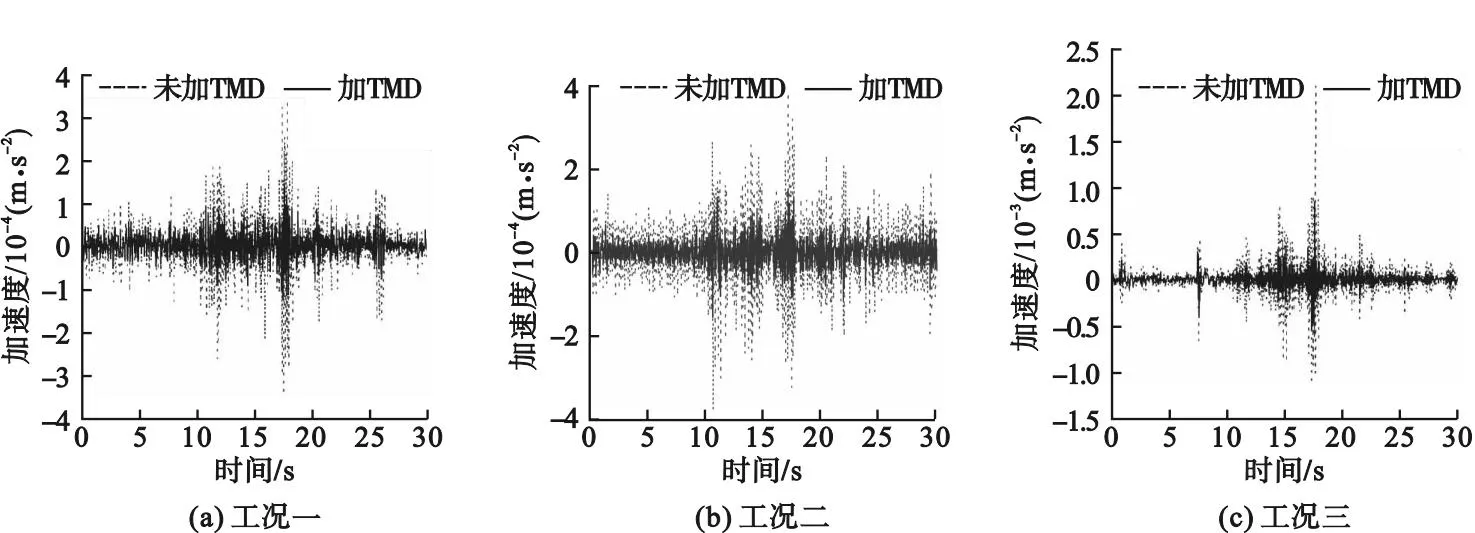
图8 A1处加速度时程曲线

从图7和图8可以看出,当TMD的质量比从0.01上升至0.02时,3种工况下加速度减小幅度均在15%以上;当TMD的质量比从0.04上升到0.05时,3种车辆荷载工况的加速度减小幅度均在3%以内。对于车辆荷载激发的微振动,在TMD质量比较小时,增加TMD的质量比,有较好的减振效果,当TMD质量比较大时,加速度降低幅度愈发缓慢。在安装TMD后,三种工况的平均加速度减小幅度最高可达到53.16%;质量比从0.01上升到0.05,三种工况的结构加速度降低幅度最高为34.47%。

TMD的质量比为0.05时,在工况一和工况二下,振动速度均达到了规范要求。TMD的质量比越大,微振动的控制效果越好,但加速度和速度的降低幅度变得愈发缓慢。

2.3 TMD安置位置

改变TMD的安置位置,分析在不同车辆荷载激励下TMD安置位置对微振动控制效果的影响。车辆荷载的振动波是靠近①轴方向传播,在靠近振源位置安置TMD,为方便安装将TMD设置在①轴与轴的交汇处(A2)。

只改变TMD安置位置,将TMD安装于A2处的减振控制效果与TMD安装于A1处减振控制效果进行对比分析。质量比取0.05,A2处安装TMD后最大振动速度结果见表4。在3种不同工况下,TMD取不同质量比时平均加速度降低幅度曲线如图9所示。工况三下,TMD质量比为0.05时,未安装TMD与安装TMD的加速度时程曲线如图10所示。TMD设置于A1和A2处的平均加速度结果见表5和表6。

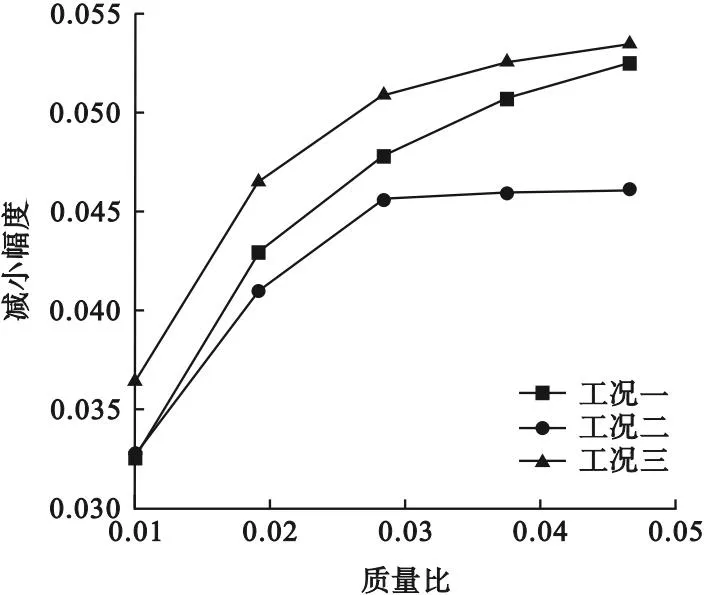
图9 A2处平均加速度降低幅度曲线

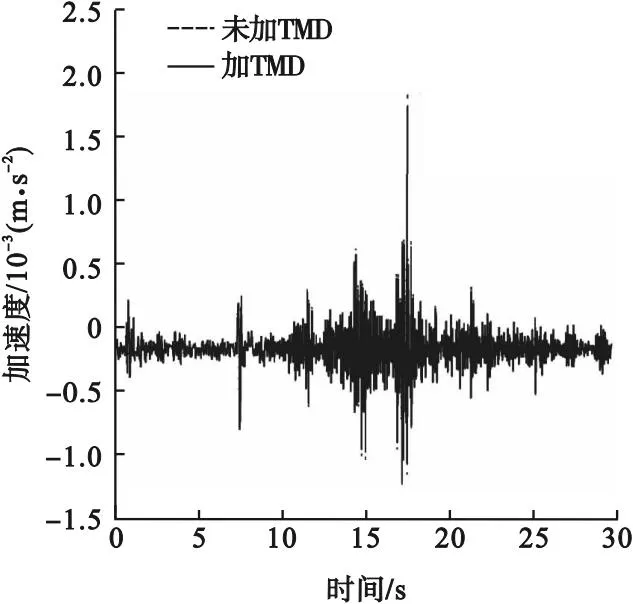
图10 A2处加速度时程曲线对比图

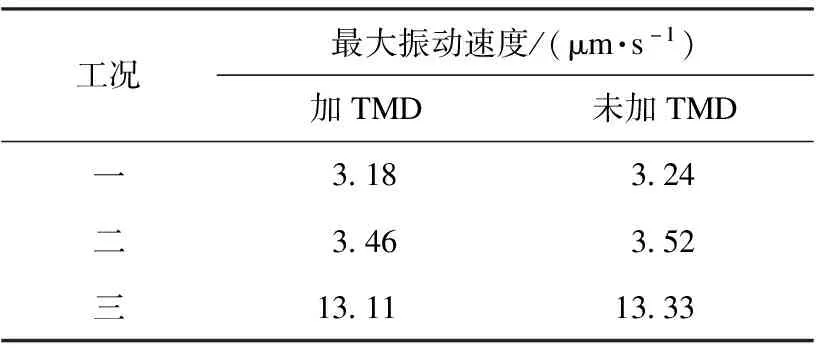
表4 A2处最大振动速度

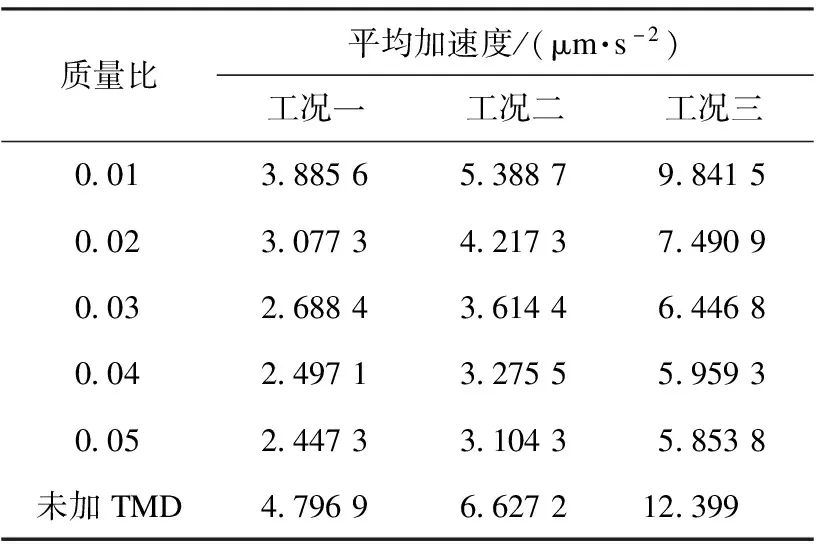
表5 A1处平均加速度

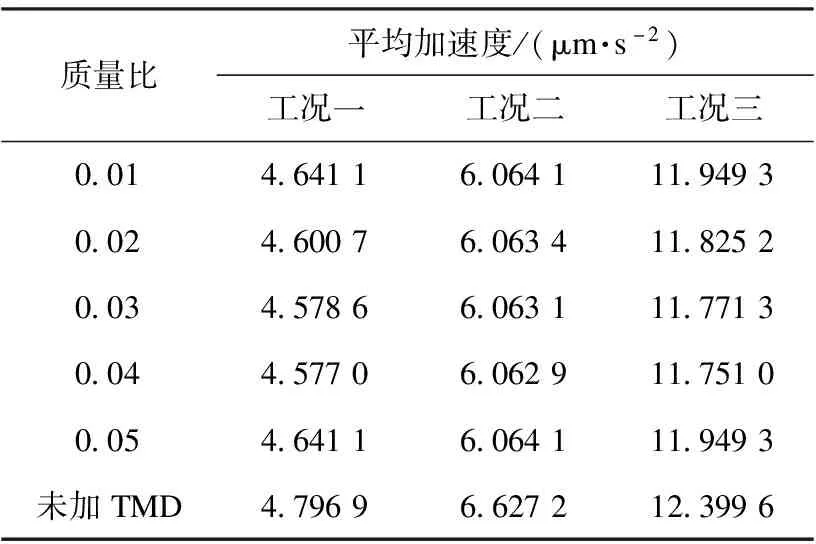
表6 A2处平均加速度

TMD安置于靠近振源的楼板上A2点,TMD对于车辆荷载激励下产生的微振动控制效果不佳,3种工况下最大振动速度均超过规范要求的3 μm/s。安装TMD在A2处的振动速度变化规律与安装于A1处一致,但TMD安装于A2时的速度降低幅度明显小于安装于A1时的速度降低幅度。

3种工况下的加速度降低幅度均在5.5%以内。TMD安置于A2时平均加速度较安置于A1时下降了约10%。TMD安置于A2时,当TMD的质量比从0.01上升至0.02时,3种工况的加速度降低幅度约提高了1%;TMD安置于A1时,加速度降低幅度远远大于A2;TMD安置于A2时,当TMD质量比从0.04上升至0.05时,3种工况的加速度降低幅度提高幅度在0.2%以内,安装在A1点处加速度降低幅度远远大于A2。改变TMD的安装位置,控制微振动的效果也会有明显的变化。

TMD安置于不同的位置,控制微振动都有相同的规律,即TMD的质量比越大,微振动控制效果越好,但加速度与速度降低幅度逐渐变缓。TMD安置于结构位移最大处的微振动控制效果要好于TMD安置于靠近激励处,TMD安置于靠近激励处后结构的最大振动速度均超过限值3 μm/s,不满足精密仪器的最大振动速度限制要求。

2.4 TMD刚度

在表4给出的TMD参数基础上,选择质量比为0.02和0.05的TMD,将TMD安装于A1点处,改变TMD的刚度,分析在车辆荷载激励下,TMD刚度改变对微振动控制效果的影响。

安装TMD后,随着TMD刚度的增大,振动速度逐渐减小,但振动速度降低幅度变得愈发缓慢。当TMD质量比取0.05时,刚度增加到原来的1.1倍,在工况三下,最大振动速度由13.33 μm/s下降至10.01 μm/s;在工况二下,最大振动速度由3.52 μm/s下降至2.77 μm/s;在工况一下,最大振动速度由3.24 μm/s下降至2.34 μm/s。分析可知,刚度变化不大时,刚度改变对减振速度影响不大。在工况一下,刚度增加到原来的1.1倍,速度时程曲线如图11所示,改变TMD刚度后的加速度降低幅度曲线如图12所示。

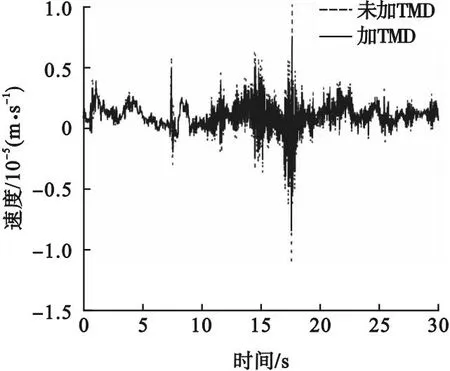
图11 1.1倍刚度下速度时程曲线对比图

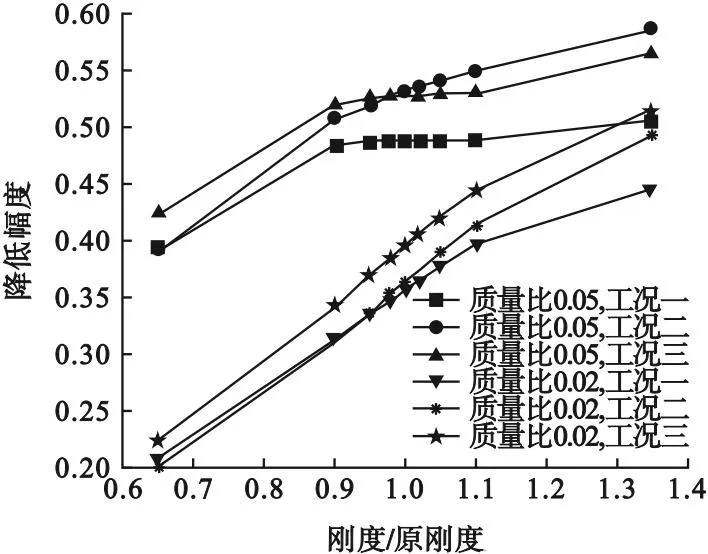
图12 改变TMD刚度后的加速度降低幅度曲线

从图12可以看出,当TMD质量比取0.02和0.05时,刚度从原刚度的65%变为原刚度的90%,三种工况下平均加速度降低幅度变化了10.64%,其中TMD的质量比取0.02时,工况三的加速度降低幅度变化了12.01%;刚度从原刚度110%变为原刚度的135%,三种工况下平均加速度降低幅度变化了4.74%,其中TMD的质量比取0.05时,工况三的加速度降低幅度变化最小,变化了1.71%。当TMD质量比取0.02时,刚度从原刚度参数的90%上升到110%,三种工况的平均加速度降低幅度变化了9.58%,三种工况的平均加速度降低幅度最高变化了达到10.31%;当TMD的质量比取0.05时,刚度从原刚度参数的90%上升到110%,三种工况的平均加速度降低幅度变化了0.14%,三种工况的的加速度降低幅度最高变化了达到0.27%。

TMD的刚度越大,微振动控制效果越好,但随着TMD的刚度增大,加速度降低幅度变化的愈发缓慢;当TMD的刚度较小时,增大TMD的刚度,加速度降低幅度变化的越快。改变TMD的刚度,与改变TMD质量比和改变TMD安装位置相比,对结构减振程度影响较小。

3 结 论

(1)笔者使用的有限元模拟验证方法是正确的,可适用于其他需要控制微振动的类似工程之中。

(2)当TMD质量比为0.05,不改变TMD的刚度,TMD安置于竖向位移最大处,在工况一和工况二下,最大振动速度满足规范要求;而且在工况二下,平均加速度降低幅度达到52.79%,平均速度减振率降低幅度达到24.47%,TMD对车辆荷载激励下的微振动有很好控制效果。

(3)相对于TMD安装于靠近激励处,当TMD安装于振动响应最大处时,减振效果较好。当TMD质量比较小时,增大TMD的质量比,减振率明显提高;当TMD质量比较大时,增大TMD的质量比对微振动控制效果影响较小。改变TMD的刚度与改变TMD质量比和安装位置相比,对结构减振影响较小。同种工况下,加速度降低幅度要高于速度降低幅度。