考虑尺寸效应的微型武器壳体动态响应分析

柴 彪，李 勇，宋修元，刘华颖，梁晓峰

(北方自动控制技术研究所，太原 030006)

1 引言

微型武器主要是指微纳米尺度的具有感知决策、行动与交互的无人作战单元。而微型武器与普通武器相比，由于尺寸效应的影响，在结构尺寸、刚度变化都有显著差异。在实验和原子模拟中都观察到了微型结构存在的尺寸效应[1-3]。因此在对微型武器壳体进行振动响应分析时应充分考虑尺寸效应对其的影响。

然而，三维石墨烯泡沫材料[4-5]，由于其有着超弹性、超低密度、高能量耗散和良好的导电性等优点，已成为材料科学领域中最受关注的热点[6-8]。尤其当石墨烯泡沫作为增强纳米材料，与石墨烯片或碳纳米管相比，它可以提供更好的结构增强效果。

近年来，对三维石墨烯泡沫增强聚合物(GFRNC)结构的研究引起了人们的广泛关注。Embrey等[9]发现GFRNC结构在电气性能、机械性能和热性能方面都有很大的提高。Li等[10]报道了由GFRNC复合材料制成的高拉伸、高灵敏度应变传感器。Jia等[11]在化学气相沉积框架下介绍了GFRNC结构的生产工艺。Guan等[12]综述了GFRNC结构在储能转换、电磁干扰屏蔽、油水分离和传感器等方面的应用。目前，国内外关于尺寸效应的微型武器三维石墨烯泡沫增强壳体的动态响应方面的研究报到很少。本文旨在对GFRNC微型武器壳体进行自由和强迫振动的研究和分析。

2 模型建立

如图1三维石墨烯泡沫增强微型武器复合壳体模型的建立，其中壳体的厚度为h、半径为R、长度为L、F为垂直于微壳表面的外部力。如图2所示，本文考虑了3种三维石墨烯泡沫分布:GFRNC-I、GFRNC-Ⅱ和GFRNC-U。

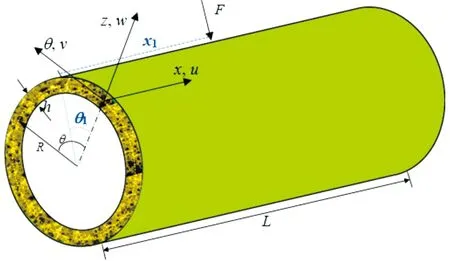
图1 三维石墨烯泡沫增强微型武器复合壳体模型Fig.1 3D graphene foam enhanced composite shell model of microweapons

在GFRNC-Ⅰ中，最大尺寸的三维石墨烯泡沫位于中面。然而，在GFRNC-Ⅱ中，最大尺寸的泡沫位于底部和顶部表面。GFRNC-U表示三维石墨烯泡沫均匀分布。其中材料性能表示为：

GFRNC-Ⅰ:

ρ(z)=ρ1[1-κmcos(πz/h)]

(1)

E(z)=E1[1-κ0cos(πz/h)]

(2)

GFRNC-Ⅱ:

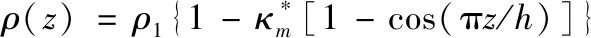
(3)

(4)

GFRNC-U:

ρ(z)=ρ1ϑ′

(5)

E(z)=E1ϑ

(6)

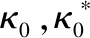
如图2(d)所示。在混合标准规则的框架下，等效质量密度ρ1,杨氏模量E1和v1泊松比可得：

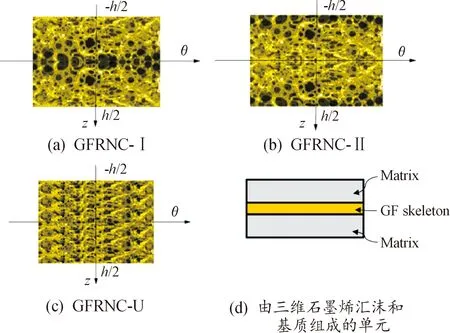
图2 不同的三维石墨烯泡沫分布类型Fig.2 Different 3D graphene foam distribution types

ρ1=ρm(1-VGF)+ρGFVGF

(7)

E1=Em(1-VGF)+EGFVGF

(8)

ν1=νm(1-VGF)+νGFVGF

(9)

其中:ρGF和ρm分别为GF骨架和环氧树脂基体的质量密度；EGF和Em分别为GF骨架和环氧树脂基体的杨氏模量；νGF和νm分别表示GF骨架和环氧基体的泊松比；VGF表示GF骨架体积分数，表示为：

(10)

其中，WGF为GF骨架的重量分数。

将式(7)代入到式(10)可得：

(11)

杨氏模量与密度的关系如下：

E(z)/E1=[ρ(z)/ρ1]2.73

(12)

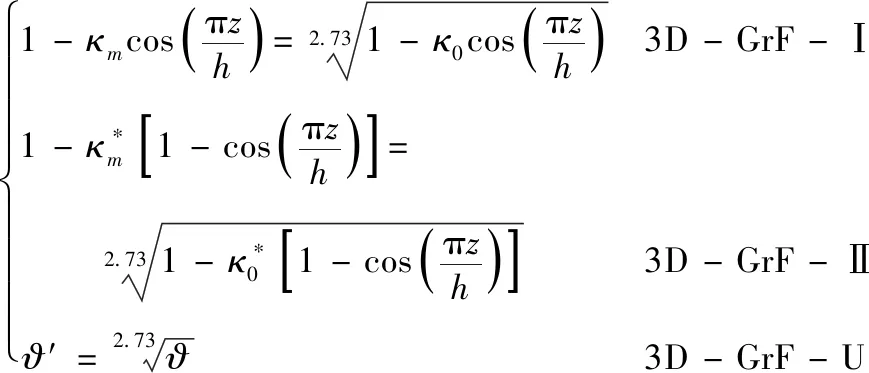
(13)

这里假设不同类型的GFRNC微壳的质量是相等的，即：

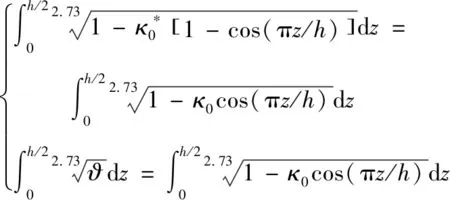
(14)

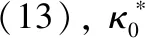
基于Love薄壳理论，位移场为：

(15)

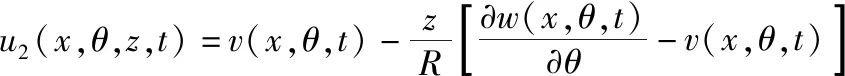
(16)

u3(x,θ,z,t)=w(x,θ,t)

(17)

GFRNC微壳的应变分量可以写成：

(18)

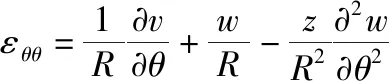
(19)

(20)

基于修正的偶应力理论[13],在考虑经典常数的基础上，引入了一个新的非经典参量，即微结构的应变能为：

(21)

其中：m表示偶应力张量；χ表示对称曲率张量；σ为柯西应力张量；ε为应变张量。这些张量具体表示为[14]:

m=2l2μχ

(22)

(23)

σ=λtr(ε)I+2με

(24)

(25)

其中：λ和μ表示拉梅常数;l表示材料长度尺度参数;u表示位移矢量；θ表示旋转向量。

通过式(21),GFRNC微壳的应变能为：

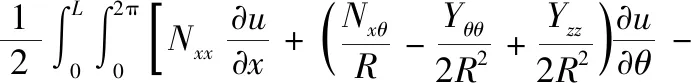
(26)

非经典和经典的力和力矩为

(27)

动能可以写成：

(28)

外力做功为：

(29)

通过哈密顿原理可得：

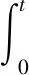
(30)

将式(26)，(28)和(29)代入到式(30),可得GFRNC微壳的运动方程为：

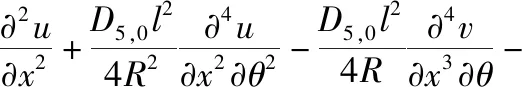
(31)

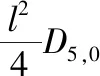
(32)

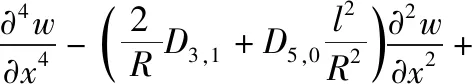
(33)

这里

其中，G(z)为GFRNC微壳的剪切模量。

3 方法求解

3.1 自由振动

满足边界条件的位移场可表示为：

(34)

v(x,θ,t)=Vmnφ(x)sin(nθ)eiωt

(35)

w(x,θ,t)=Wmnφ(x)cos(nθ)eiωt

(36)

式中：ω表示自然圆频率；m和n表示模态数；Umn,Vmn和Wmn表示位移振幅分量。

其中，轴向模态函数φ(x)可写为：

(37)

这里参数c1,c2,c3,c4,ζi和λi(i=1,2,3,4…) 在表1中列出。本文考虑了固支-固支(C-C)边界条件、固支-简支(C-SS)边界条件和简支-简支(SS-SS)边界条件。

表1 参数c1,c2,c3,c4,ζi和λi取值Table 1 The value of paramater c1,c2,c3,c4,ζi and λi

固支边界条件为：

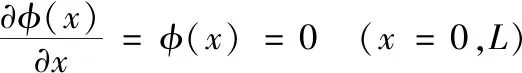
(38)

简支边界条件为：

(39)

将式(34)—(36)代入到式(31)—(33)与此同时忽略外力F,之后采用Galerkin法[15-17]可得：

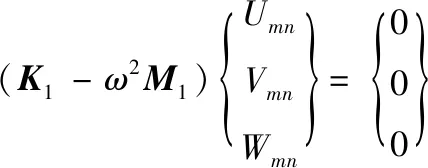
(40)

其中，K1和M1分别表示刚度矩阵和质量矩阵。为了得到式(40)的非平凡解,系数矩阵的行列式必须设为零，才能得到GFRNC微壳的固有频率。

3.2 强迫振动

本节以GFRNC微壳在SS-SS边界条件下的强迫振动为例进行强迫振动分析，其中外力为[18]：

F=P0sin(ω1t)δ(x-x1)δ(θ-θ1)

(41)

式中：P0为激励力幅值;ω1为激励圆频率;(x1,θ1)为激励的位置;δ表示狄拉克函数。

对于强迫振动，SS-SS的GFRNC微壳的位移场可表示为：

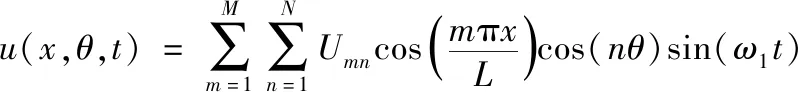
(42)

(43)

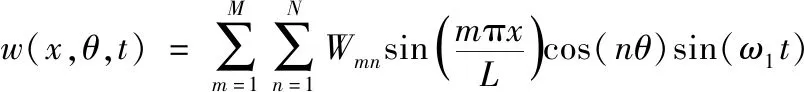
(44)

其中，M和N表示截断系数。

将式(41)—(44)代入到式(31)—(33)后利用Galerkin法消去三角函数，可得：

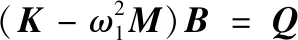
(45)

式中：B={UmnVmnWmn}T表示微壳的振幅矢量;Q={0 0P0cos(nθ1)sin(mπx1/L}T表示激励的常矢量;K和M分别表示刚度矩阵和质量矩阵。

式(45)的解可得：

(46)

因此，横向振动振幅wmax可由式(44)得出。

4 结果对比与分析

4.1 对比

首先进行对比验证。本文中对SS-SS、C-SS和C-C均质圆柱壳进行了对比研究。它们的无量纲固有频率列于表2—4。结果表明，本文的计算结果与已发表论文的结果吻合较好[19-22]。

表2 SS-SS均质圆柱壳的无量纲固有频率对比 (R=2.32 nm,L/R=5,ρ=2 300 kg/m3,υ=0.3和E=1.06 TPa)Table 2 Dimensionless natural frequency comparison of SS-SS homogeneous cylindrical shells (R=2.32 nm,L/R=5,ρ=2 300 kg/m3,υ=0.3 and E=1.06 TPa)

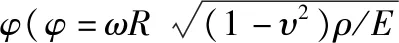
表3 C-SS均质圆柱壳的无量纲固有频率对比 (υ=0.3,h/R=0.002,L/R=20和m=1)Table 3 Dimensionless natural frequency comparison of C-SS homogeneous cylindrical shell (υ=0.3,h/R=0.002,L/R=20 and m=1)

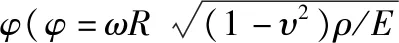
表4 C-C均质圆柱壳的无量纲固有频率对比(h/R=0.01,L/R=20,υ=0.3和m=1)Table 4 Dimensionless natural frequency comparisonof C-C homogeneous cylindrical shell (h/R=0.01,L/R=20,υ=0.3 and m=1)

其次，考虑尺寸效应，表5给出了SS-SS微纳米圆柱壳的无量纲固有频率的比较。可以看出，本文中的结果与文献中一致。

表5 含尺寸效应的SS-SS微纳米圆柱壳的无量纲固有频率对比 (l=h,R=2.32 nm,L/R=5,E=1.06 TPa,υ=0.3和ρ=2 300 kg/m3)Table 5 Dimensionless natural frequency comparison of SS-SS homogeneous cylindrical shell with size effect (l=h,R=2.32 nm,L/R=5,E=1.06 TPa,υ=0.3 andρ=2 300 kg/m3)

接下来，对GFRNC微壳的振动进行了研究。未指定时，GFRNC微壳的几何和材料参数为:

EGF=1.02 TPa,ρGF=2 300 kg/m3,νGF=0.3

Em=3 GPa,ρm=1 200 kg/m3,νm=0.34,l=15 μm

m=1,h=20 μm,R/h=50,L/R=3

WGF=1.0%,κ0=0.2

4.2 自由振动

图3对比了不同理论下SS-SS GFRNC微壳的固有频率。从图中可以看出，考虑修正的偶应力理论(MCST)的固有频率随尺度参数的增大而增大，而经典理论(CT)的固有频率不随尺度参数的增大而变化。这是因为尺寸效应会增加GFRNC微壳的刚度。然而，经典壳理论没有考虑这一效应，因此得到了不准确的结果。

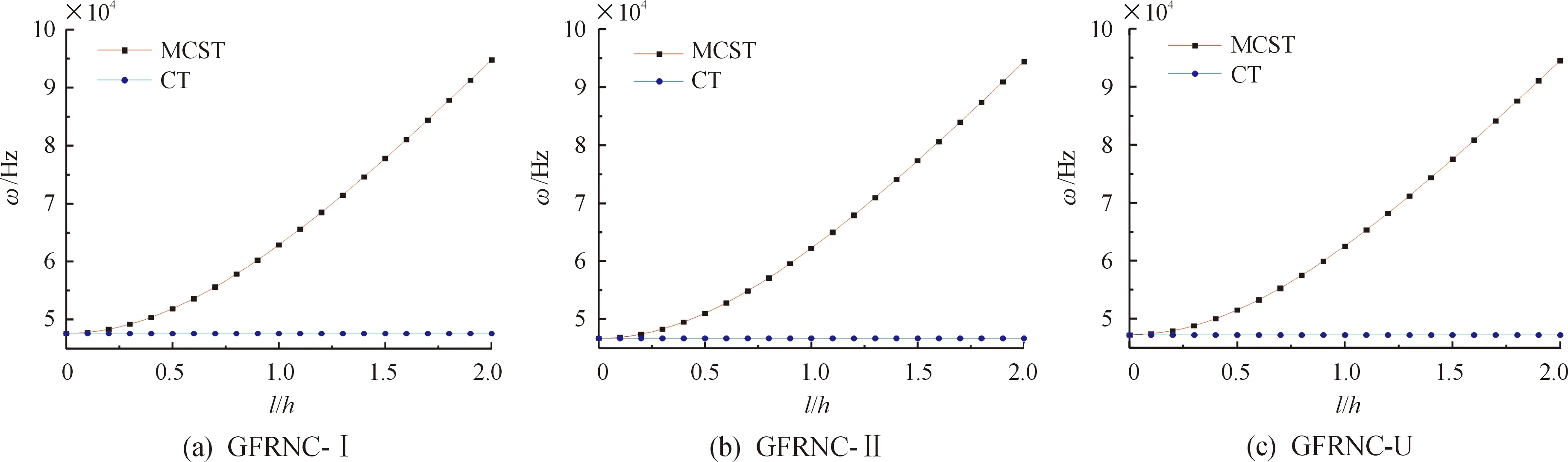
图3 无量纲长度尺度参数l/h对SS-SS GFRNC微壳固有频率的影响Fig.3 The effect of dimensionless length scale parameter l/h on SS-SS GFRNC microshell natural frequency

不同边界条件下周向波数对GFRNC微壳固有频率的影响如图4所示。从图中可以看出，随着周向波数的增加，固有频率先减小后增大。最小固有频率出现在n=3时。因此，在接下来的分析中，本文选择GFRNC微壳的最低模态(m=1,n=3)作为代表模态。此外，可以看出GFRNC微壳在SS-SS边界条件下的固有频率最低，C-C边界条件下的固有频率最高。

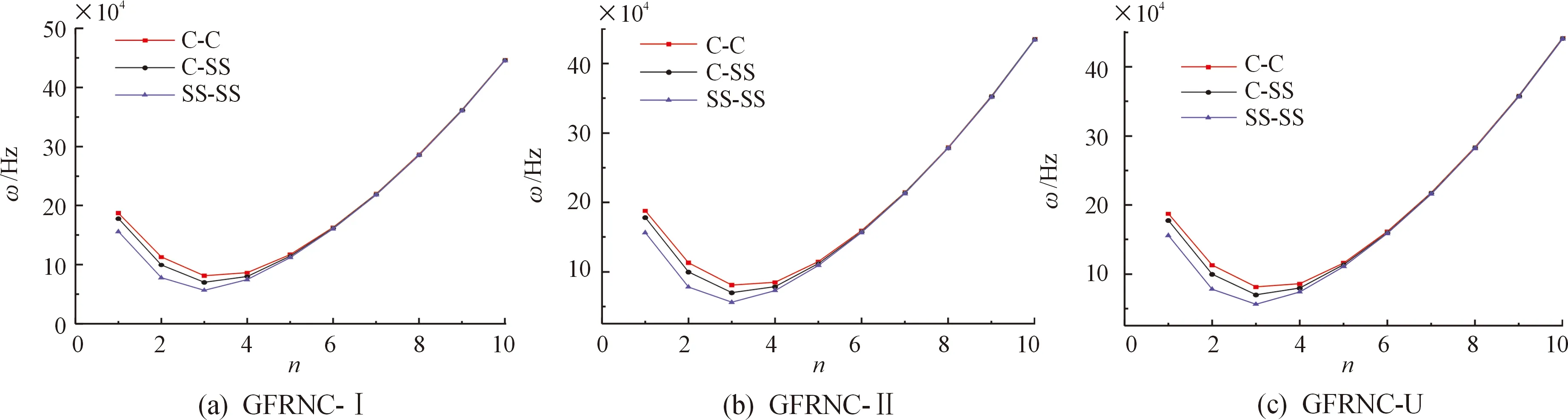
图4 周向波数n对GFRN微壳固有频率的影响Fig.4 The effect of circumferential wave number n on GFRN microshell natural frequency

三维石墨烯质量分数对GFRNC微壳固有频率的影响如图5所示。结果表明，随着三维石墨烯质量分数的增加，其固有频率也随之增加。可以看出，即使在聚合物基体中加入少量的三维石墨烯泡沫，微壳的刚度也能明显增强。此外，GFRNC-Ⅰ壳的结构刚度频率最低，而GFRNC-Ⅱ壳的结构刚度频率最高，说明GFRNC-Ⅰ增强微壳的结构刚度最好。

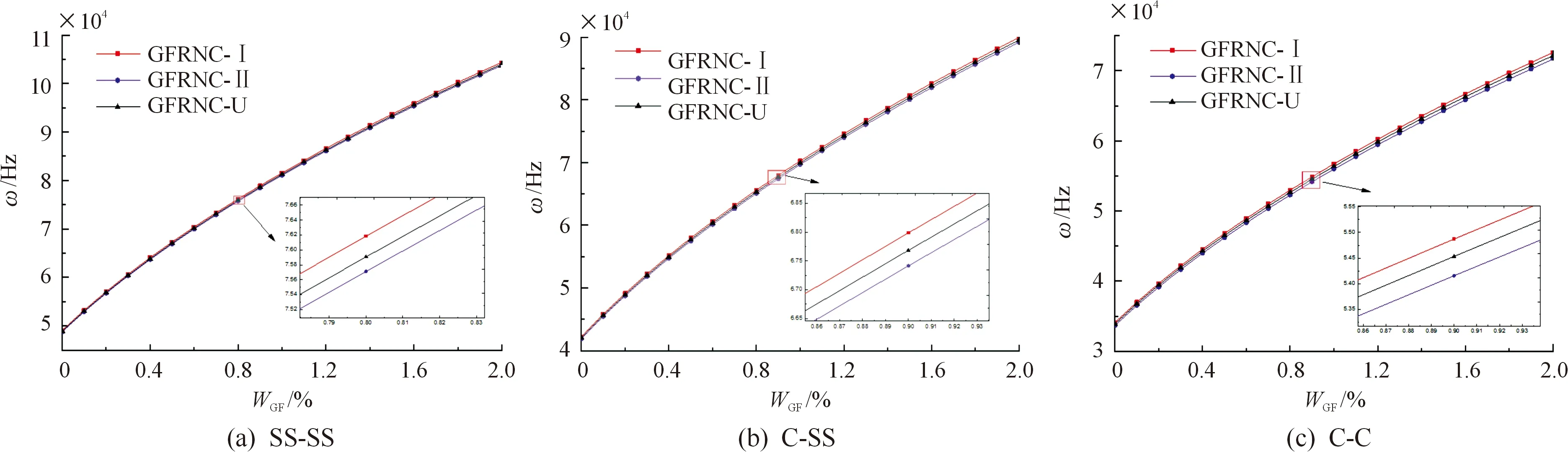
图5 不同边界条件下三维石墨烯质量分数WGF对固有频率的影响Fig.5 Influence of 3D graphene mass fraction WGF on natural frequency under different boundary conditions

图6给出了不同边界条件和泡沫系数对GFRNC微壳固有频率的影响。结果表明随着泡沫系数的增大，GFRN微壳的固有频率减小;此外，随着泡沫系数的增加，GFRNC-U微壳的固有频率下降速度快于GFRNC-Ⅱ微壳。最后，除SS-SS边界条件外，GFRNC-U微壳具有最低的固有频率。

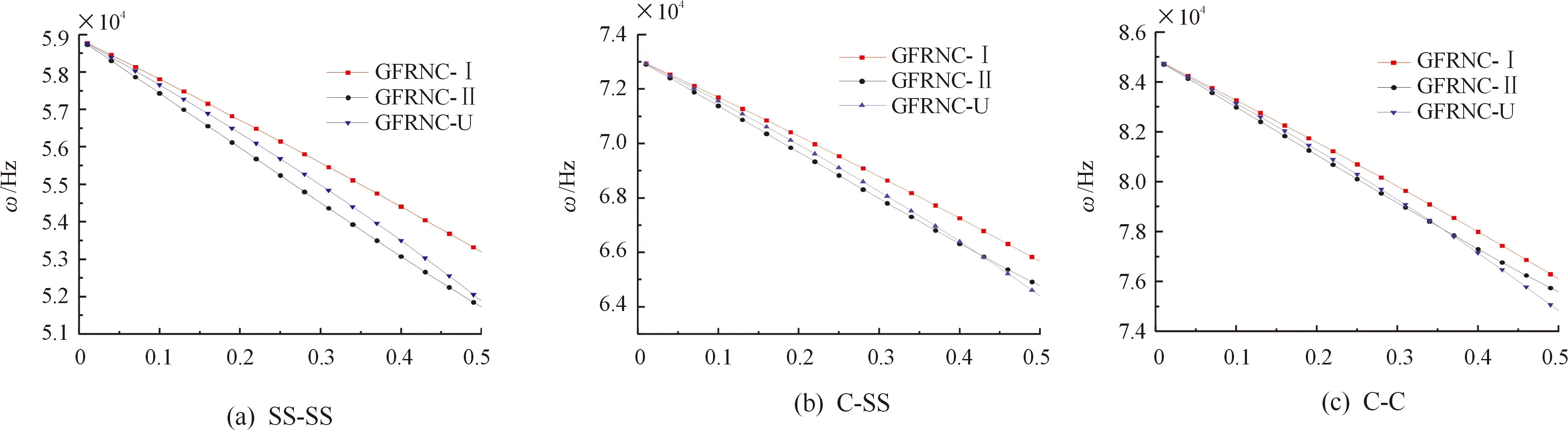
图6 不同边界条件下泡沫系数κ0对固有频率的影响Fig.6 Influence of foam coefficient κ0on natural frequency under different boundary conditions

4.3 强迫振动

如表6所示，首先进行稳态谐波载荷下SS-SS GFRNC微壳中心点振幅收敛性分析。可以看出，当截断系数分别达到M=75和N=75时，可以得到很好的收敛效果。因此这些截断系数将在下面的分析中使用。

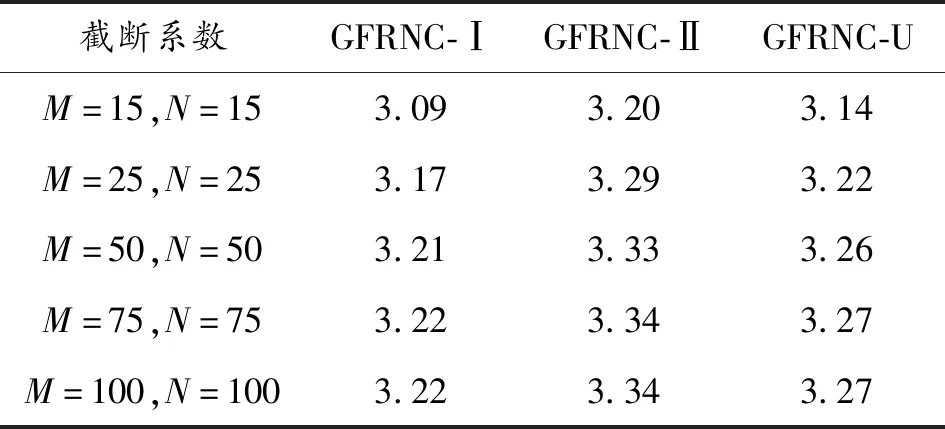
表6 SS-SS GFRNC微壳振幅wmax (10-4 m) 的收敛性验证 (x=L/2,θ=0°,x1=L/2,θ1=0°,P0=1 000 N,ω1=2×105 rad/s)Table 6 Convergence verification of SS-SS GFRNC microshell amplitude wmax (10-4 m) (x=L/2,θ=0°,x1=L/2,θ1=0°,P0=1 000 N,ω1=2×105 rad/s)

图7为不同泡沫系数下GFRNC-Ⅰ微壳中心点的频响曲线，其中x=L/2,θ=0°,x1=L/2,θ1=0°和P0=1 000 N。结果表明，泡沫系数较大的微壳容易发生共振，而泡沫系数较小的微壳不易发生共振。

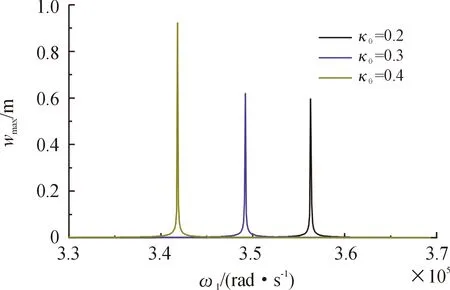
图7 不同三维石墨烯泡沫系数下的GFRNC-Ⅰ微壳频响曲线Fig.7 Frequency response curves of GFRNC-Ⅰ microshells with different 3D graphene foam coefficients

不同三维石墨烯泡沫类型的GFRNC微壳中心点的频响曲线如图8所示。其中x=L/2,θ=0°,x1=L/2,θ1=0°和P0=1 000 N。结果表明:随着激励频率的增加，GFRNC-Ⅱ微壳首先发生共振，而GFRNC-Ⅰ微壳最后发生共振。这表明增强共振频率最有效的方法是在近内、外表面分布致密三维石墨烯泡沫，在近中平面减少三维石墨烯泡沫。

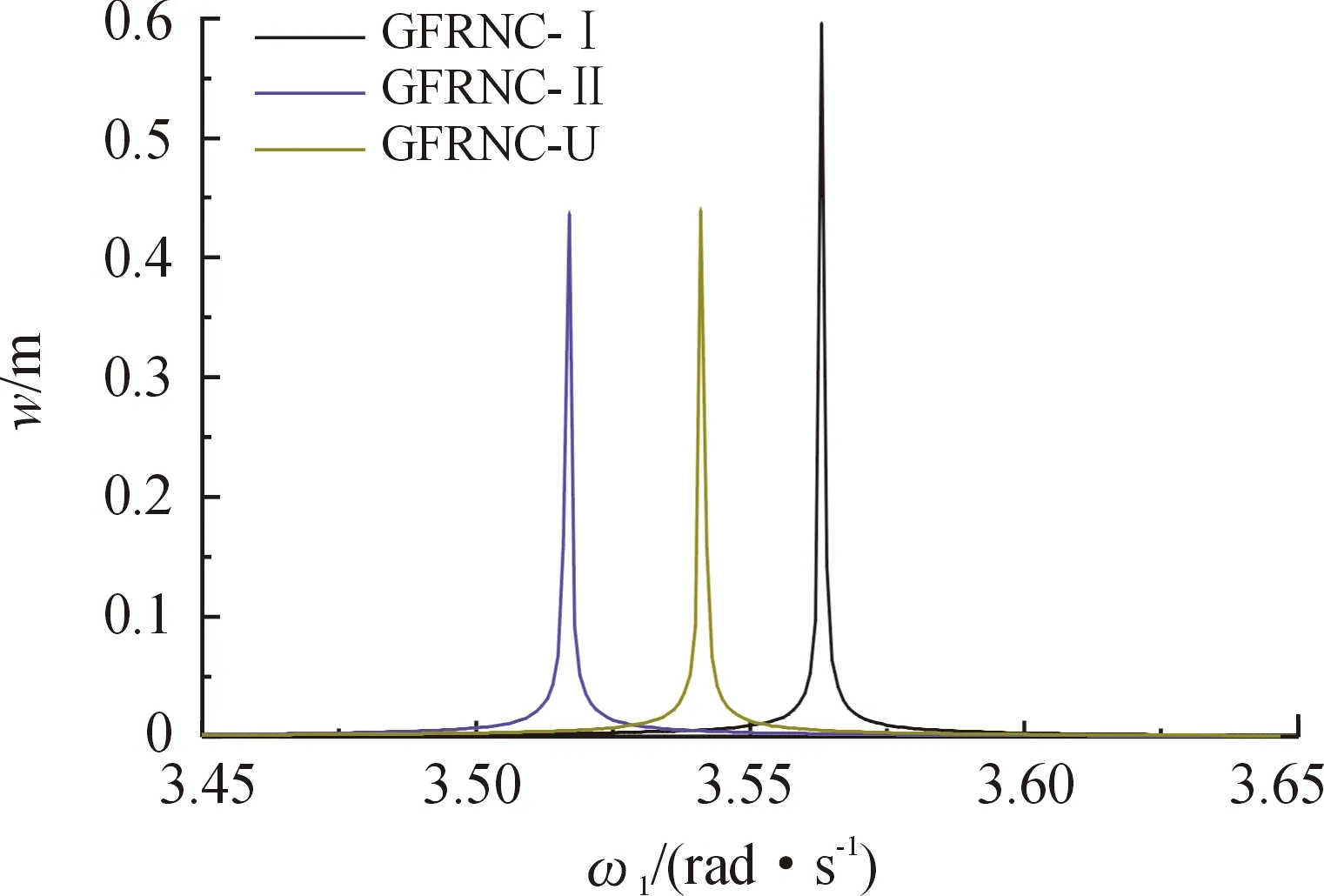
图8 不同三维石墨烯泡沫类型的GFRNC微壳频率响应曲线Fig.8 Frequency response curves of GFRNC microshells with different 3D graphene foam types

图9给出了不同三维石墨烯泡沫重量分数分布下GFRNC微壳中心点的频响曲线，其中x=L/2,θ=0°,x1=L/2,θ1=0°和P0=1 000 N。可以看到，具有较大三维石墨烯泡沫重量分数的微壳更难以共振。因此，三维石墨烯泡沫的加入使微壳结构更加稳定。

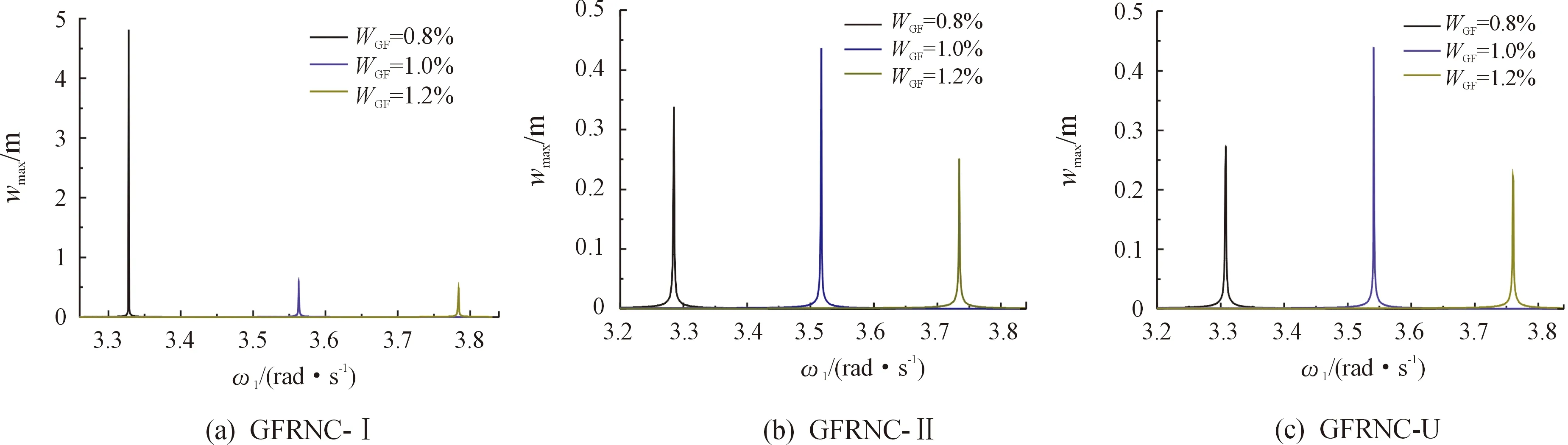
图9 不同三维石墨烯泡沫重量分数分布下的GFRNC微壳频响曲线Fig.9 Frequency response curves of GFRNC microshells with different 3D graphene foam weight fraction distributions

5 结论

以上通过一种新型的微型武器增强壳体结构模型建立以及进行的考虑尺寸效应的动态响应分析，结果表明：尺度参数、三维石墨烯泡沫系数、分布类型和重量分数对GFRNC微型武器壳体的动态响应有着重要的影响。其中固有频率随三维石墨烯泡沫重量分数的增加而增大，表明三维石墨烯泡沫能显著提高GFRNC微壳的力学性能。此外，固有频率还随三维石墨烯泡沫系数的增大而增大。当泡沫系数较小时，GFRNC-Ⅰ微壳的频率最低，而GFRNC-Ⅱ微壳的频率最高。当泡沫系数较大时，除SS-SS边界条件外，GFRNC-U微壳始终具有最低的固有频率。与此同时，在GFRNC微型武器壳体的内外表面致密化三维石墨烯，并且壳体的中平面减少该含量，具有最好的增强效果。这为三维石墨烯泡沫应用于微型武器装备提供了理论指导和技术支撑。