基于线性自抗扰的并联液压系统同步控制

廖 亮，向国菲，郑秀娟，朱雨琪，肖 权，佃松宜

(四川大学电气工程学院，成都 610065)

0 引言

并联液压系统由于结构简单、可靠性高及大负载等显著优势，作为驱动系统被广泛应用于重载工程设备中。某盾构隧道使用穿行式隧道弧形件安装机[1]对预制弧形件进行拼接，为有效避免倾覆等工程事故，需提高多源不确定性条件下的同步性精度，因此，研究多并联液压系统同步控制对实际工程应用有着重要的指导意义。

目前，国内外众多学者对液压系统及其并联系统的同步控制问题展开了广泛研究[2-10]。江桂云等[2]在理想条件下推导了其传递函数，但未考虑多液压系统协同；杨文斌、陈杰等[3-4]利用遗传算法整定PID参数，在一定程度上提高了同步性，但参数的寻优过程十分复杂且时间成本长。YAO、张颖等[5-8]提出结合模糊理论与PID控制与解耦补偿算法，改善了多液压缸的同步控制精度，但控制器复杂且参数整定困难。HAN等[9]提出一种自适应滑模控制方法，对主从同步控制性能进行了分析研究，其结果优于模糊PID控制。PAN等[10]针对多缸同步控制的问题，提出基于BP神经网络的主从同步控制策略，提高了多缸同步控制的精度。但该方法的控制器结构过于复杂且耗时。因此，如何在不依赖于系统精确模型的条件下，设计一个结构简单、抗干扰能力强、鲁棒性好的控制器来提高多液压系统同步性，对于大型工业工程的实践应用有着重要意义。

自抗扰控制(active disturbance rejection control，ADRC)，其核心将被控对象自身的不确定性与外部干扰一并视作“总扰动”[11-12]，利用扩张状态观测器(extended state observer，ESO)进行实时估计并补偿。由于其不依赖精确的模型，因此是一种工程性很强的控制方法[13]。梁青、王立新等[14-17]基于自抗扰控制对液压活塞杆位置同步进行分析研究，但并未考虑多系统的参数不确定性。刘丽贞等[18]提出带宽法来整定控制器参数，使得控制器结构进一步简化。

上述关于并联液压系统的同步控制文献，均为理想系统模型，未考虑实际工况与参数不一致性的影响，同时控制器结构相对复杂。基于此，本文综合液压系统参数不确定性、内外扰动等复合影响因素的情况下，研究了并联液压系统的同步性问题。将参数不确定性、建模不确定性、扰动不确定性等多种不确定性问题转化为“总扰动”的抗扰问题，设计了基于线性自抗扰的同步控制器。最后，在AMESim仿真平台搭建了双液压系统模型，结合MATLAB/Simulink构建的控制器，进行联合仿真实验，仿真结果验证了提出的理论的有效性。此外，与传统的PID控制方法相比，本文提出的控制策略的同步误差更小，精度更高。

1 问题描述与系统建模

本文以某穿行式隧道弧形件安装机的行走系统为研究对象，采用四通滑阀控非对称液压缸结构，由双作用单活塞杆、三位四通换向阀等组成，其原理如图1所示。qij(i,j=1,2)分别为流入与排出并联液压系统两个活塞缸的流量；xip(i=1,2)分别为并联液压系统的换向阀位移；PT为回油压力；Ps为原油压力。系统在运行过程中受到环境变化、未知外部干扰、液压油性质随温度等因素发生变化、组成液压系统的元器件生产加工与安装精度等影响，造成该安装机的行走系统同步性差，而同步性将直接影响系统运行正常与否，严重会发生工程事故。因此，本文对其同步性开展研究。

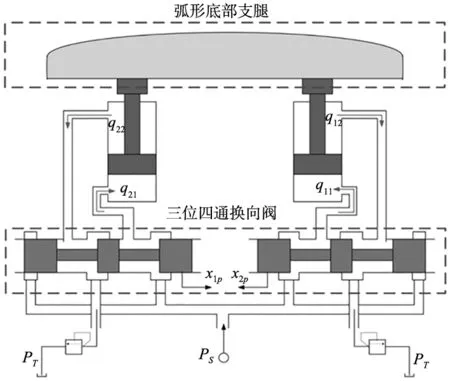
图1 行走系统双液压原理图

1.1 流量方程

由流量连续性方程可以得到进入系统与排除系统的流量分别为：

(1)

式中，A1、A2为液压缸两侧有效面积；V1、V2为液压缸两腔有效容积；p1、p2为左右两腔的作用压力；Cip、Cep为内外泄漏系数；q1、q2为系统流入与排出的流量；x为活塞杆位移；βe为液压油的有效弹性体积模量；V1=V10+A1x；V2=V20-A2x；V10、V20分别为左右工作腔初始容积。

液压系统工作时，活塞需往复运动，即需要切换液压油流入与排出的方向，因此定义方向函数为：

(2)

结合阀口流量公式[2]，以及阀芯对液压系统的输入的比例响应环节，可得：

(3)

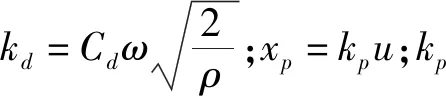
为进一步简化式(3)的表达，记：

代入式(3)可以得到：

(4)

1.2 力平衡方程

根据牛顿第二定律可建立液压缸与负载的力平衡方程：

(5)

式中，m为活塞及液压缸负载等效质量；Bp为活塞与负载的粘性阻尼系数；K为负载的弹性刚度，本系统无弹性负载，故此处K=0；d为系统外部扰动。

结合式(1)、式(4)和式(5)，考虑系统未建模态特性，可以得到以下动力学平衡方程：

(6)

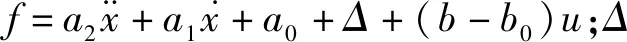
根据系统的力平衡方程可以看出，本盾构隧道安装机的液压驱动系统是一个具有扰动不确定性、建模不确定性、模型参数摄动等特点的非线性时变系统。这些因素都影响了安装机运行过程中单个液压缸活塞杆控制精度以及并联液压缸的同步精度，从而导致常规的控制器难以实现较好的同步控制性能。

2 控制器设计

为了提高并联液压系统的同步控制精度，本文提出了基于线性自抗扰的同步控制策略。主要由线性扩张状态观测器(liner extended state observer，LESO)，线性状态误差反馈控制律(liner state error feedback，LSEF)以及被控对象3部分组成。LESO是LADRC的主要组成部分，能够实时在线估计包括系统建模误差、生产导致的元器件参数不完全相同，整机安装误差、外部不确定时变扰动等在内的“总扰动”状态，并进行补偿。设计时采用观测误差与并联液压系统实际位置偏差相结合的“总误差”加以线性同步权重的形式，分别输入两个系统的观测器，从而提高整个系统的鲁棒性和扰动抑制能力。避免了标准液压系统的选择。其控制框图如图2所示。

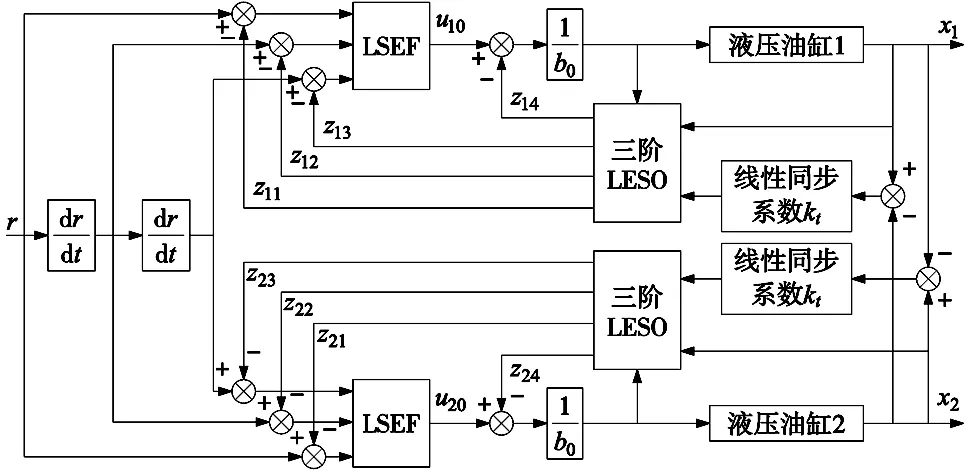
图2 基于LADRC的同步控制系统框图

2.1 LESO设计

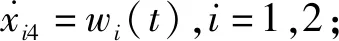
(7)

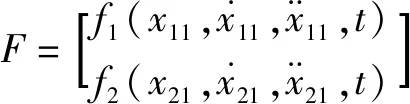
对1号液压系统设计如下所示的线性扩张状态观测器：

(8)

同理，对2号液压系统设计如式(9)所示的线性扩张观测器：

(9)

(10)

通过带宽法可简化参数的整定，有效的减小了控制器的设计难度。

2.2 LSEF设计

LSEF将LESO的输出差值作为状态反馈误差，并将这些误差做线性加权来完成误差反馈。线性误差反馈控制率可写为：

ui0=k1ei1+k2ei2+k3ei3

(11)

式中，eij=r(j-1)-zij,i=1,2,j=1,2,3；i为液压油缸的序号。

将总扰动的观测值以前馈补偿的方式加到输入端，从而实现对扰动的补偿，被控对象的输入信号为：

(12)

3 仿真及分析

为验证自抗扰控制在多液压系统同步性上应用的可能性，本文在AMESim中搭建除了控制器以外的行走系统模型，并预留了通信接口，如图3所示；在Simulink中构建了控制器，将在AMESim中搭建的模型封装成模块导入其中，作为被控对象，如图4所示；通过Simulink与AMESim两个仿真平台做了联合仿真实验。

图3 AMESim模型图

图4 控制结构图

在并联液压系统模型搭建的过程中，结合实际工况，有差异的设置两个液压系统的主要参数以及负载大小，以模拟实际系统的生产加工精度不同带来的影响，主要参数设置如表1所示。

表1 主要参数设置

系统运动过程中，将负载均分至双液压系统，但实际随着时间推进，双液压缸活塞杆位移会产生微小偏差，为了消除这些微小偏差导致的负载不均衡分配对系统的影响，在两液压缸活塞末端分别模拟施加F1=16 000 N，F2=10 000 N的预设压力，同时将其视作外部扰动交由控制器一并处理。仿真参数设置t=100 s，步长T=0.001，参考指令信号设为r(t)=0.4sin(0.04πt)+0.4。

将基于LADRC的控制结果与PID控制进行了对比仿真。该双液压系统对给定参考信号的跟踪仿真结果、同步误差仿真结果如图5所示。

图5 系统轨迹跟踪及同步误差结果图 图6 速度、压力、流量变化曲线

基于LADRC的同步控制策略下的双液压系统活塞速度、液压缸两腔的压力 、流量变化曲线如图6所示。

仿真结果表明，在不同的预设负载压力，且为加入噪声时，短暂的回调现象后，基于LADRC控制的双油缸系统能快速准确的跟踪上给定的参考信号曲线，且系统稳定后的同步精度优于PID控制下的结果。通过数据分析，基于本文LADRC的同步控制作用下，系统稳定后，双油缸系统的同步控制精度为0.07 mm，占总行程的0.009%，即两活塞杆的同步性误差几乎为0，且其误差曲线相比PID控制下的误差曲线更加平滑。

为验证系统的抗扰能力，在80 s后加入外部时变的随机噪声，结果表明，加入正弦、方波等有规律的干扰时，系统与上述未加入干扰时的结果基本一致，由于篇幅等原因，此处不再展示。为进一步 贴合实际工况，本文还对随机干扰进行了验证，其结果如图7所示。

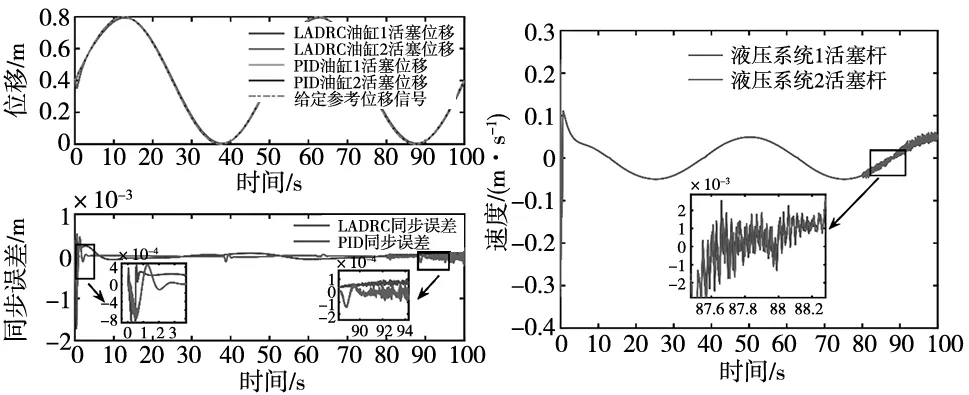
图7 随机干扰下的轨迹跟踪及同步误差结果图 图8 随机干扰下的活塞速度曲线图

其中，含随机干扰影响下，基于LADRC的同步控制策略的并联液压系统活塞速度、液压缸两腔的压力、流量变化曲线分别如图8～图10所示。

图9 随机干扰下的压力曲线图 图10 随机干扰下的流量曲线图

图7结果表明，加入时变的随机干扰后，系统对给定信号仍有较好的跟踪效果，且基于LADRC的同步控制策略下的波动更小，同步精度更高。图8～图10结果表明，基于LADRC的同步控制策略下，加之活塞末端施加不同预设压力与随机扰动的共同作用，导致两液压系统的腔内压力与流量略有区别，即使在波动的情况下，并联液压系统的两活塞速度、腔内压力、流量变化仍有着较高的同步性，也展现出了较好的一致性，且波动幅度不大，在一定程度上对未知的时变干扰具备有效的抑制能力，进一步验证了本文所提控制器对双液压系统同步性控制的较好控制性能。

以上的仿真结果验证了本文所提基于LADRC的同步控制器对双液压系统同步控制的良好控制性能，相比于传统的PID控制，其展现了更小的跟踪误差，更强的抗干扰能力，速度变化曲线平滑，鲁棒性更好。与此同时，使用这一控制方法不依赖于被控对象的精确建模，对参数繁多复杂的液压元件系统的控制及实际工程应用具有一定实践指导意义。

4 结束语

本文以并联液压系统为例，考虑实际工况下由于生产安装等误差造成的多液压系统主要参数不同，以及系统运行过程中的不确定扰动对并联液压系统同步性的影响，展开了同步控制研究。综合考虑未精确建模以及存在不同未建模态、不同时变扰动的情况下，利用基于LADRC的同步控制策略对该系统进行了仿真验证。仿真结果表明，所提控制方法能够较好的实现对给定信号曲线的跟踪，在双液压缸腔内压强、流量以及双活塞位移、速度层面均有较好的同步性。本文所提控制器结构件简单，在工程实践中具有一定指导意义，对工程中多液压系统协同作业的控制提供了新的方法与思路。