基于电压相似性评估的低压配电网户变关系和相位识别技术研究

杨虎臣，王晓东，史志鹏，王金明，陈凯，吴恒

(1.国网山西省电力公司长治供电公司，山西 长治 046011； 2.国电南瑞科技股份有限公司，南京 211000； 3.东南大学 电气工程学院，南京 210096)

0 引 言

随着电网状态估计技术的发展，电力系统拓扑结构分析方法得到了专家和学者的广泛重视，传统的电力系统拓扑分析方法一般将拓扑结构表述为链表关系，用图论中的搜索技术，如深度优先搜索法和广度优先搜索法分析节点的连通性。这种方法一般需要建立反映拓扑结构的链表，通过处理链表实现拓扑分析[1]。现代配电网系统中，中高压配电网的结构以及拓扑关系已经十分清晰，但是低压配电网由于很多小区的资产分配不清晰，甚至很多农电或者城中村地区并没有结构记录信息，拓扑结构不明确，导致电网的状态估计很难进行，同时拓扑也是线损分析和故障定位的基础，错误的拓扑信息制约着线损分析的准确性和故障处理的有效性。

随着智能电网建设的不断推进，高级量测体系(Advanced Meter Infrastructure，AMI)在配电网中配置越来越多，这为配网拓扑关系的校验与修正提供了有效的数据信息[2]。基于AMI量测数据的配电网拓扑错误研究已引起了相关研究者的重视，但仍处于起步研究探索阶段[3-5]。文献[6]提出了一种基于AMI量测信息的低压配电网拓扑校验方法，通过支路电流相关性分析结果以及负荷的耦合点电压分布，完成低压配电网络拓扑的校验与修正；文献[7]从多空间辐射与多序列窗户截面层次融合，以及多时间相关性层次，实现三维时空特性的低压配电网拓扑识别方法，文献[8]针对城市低压配电网，设计了基于多元线性回归求解的拓扑检验方法。已有研究中需要根据电流相关性进行求解分析，而实际中存在一定量的用户常年无用电记录，影响拓扑识别的判断。

文章从低压配电网电压相似性的角度，进行基于节点电压相似性评估的低压配电网户变关系和相位识别研究，首先面向AMI获取的96点电压数据，分析了利用电压相似性进行户变关系和相位识别的可行性；接着应用Hausdorff距离，构建了基于电压相似性评估的识别流程，设计了识别基本判据，以及包括构建滑动窗口和筛选有效电压的数据集优化方案；最后通过实际案例，对比分析直接应用基本判据和经过数据集优化的识别准确率，验证了方案的有效性。

1 低压配电网电压相似性分析

一般低压配电网均由独立或者两台互为备用的台区变压器降压后，通过辐射式的线路接入各末端用户，拓扑一般包括分支箱式结构、密集母线槽式结构和传统线路辐射式结构。

不同台变的电压一般存在明显的差异性，图1为AMI获取的实际运行的7个非相邻台区某日的A相96点电压数据，可见当日的电压波形相似度低。这是由于末端用户负荷在时间维度和能量维度的差异性大，当不同台区接入的中压配电网位置不同，使得台区间的电压呈现不同水平。

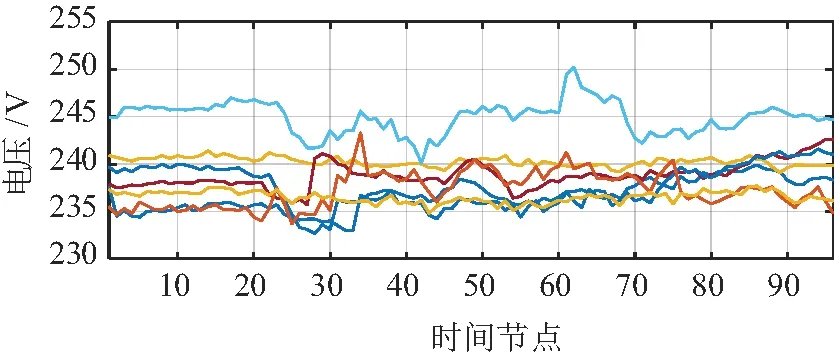
图1 不同台区日电压分布曲线Fig.1 Daily voltage distribution curve in different stations

但是当两个台区接入相同的中压配电节点，电压将存在一定的相似性，但由于台变参数差异性，导致相邻台区的电压曲线相似性将小于同台区内节点的电压相似性[9]。图2是两个相邻台区台变侧A相与其中1个台区的用户侧A相电压分布曲线，相对于图1所示的非相邻台区，相邻台区的台变侧电压分布呈现相似性，虽然差异很小，但还是可以看出用户侧的电压相似性是大于相邻台区的电压相似性的。

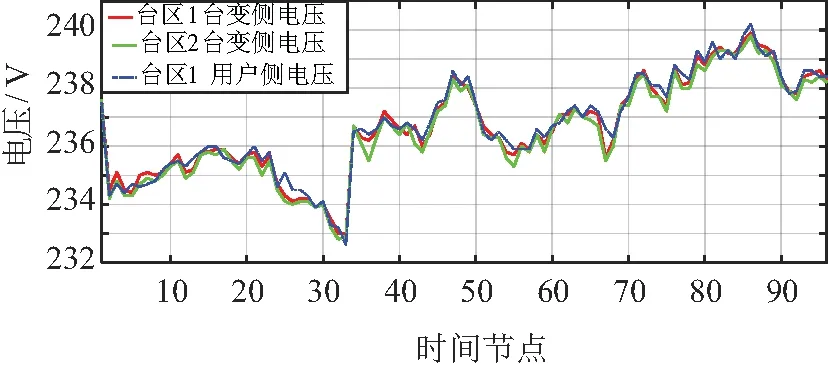
图2 相邻台区与台区内节点日电压分布曲线Fig.2 Daily voltage distribution curve between adjacent stations and nodes in same station

末端用户又分为单相负荷和三相负荷用户，同一个台区的不同相电压因为相位不同和接入负荷的数量和使用方式不同，也存在明显差异[10]。由图3所示的同一台区同一日三相电压分布曲线可见，虽然趋势呈现一致性，但是仍然存在差异；但相同相台变侧和用户侧的电压相似性略大。

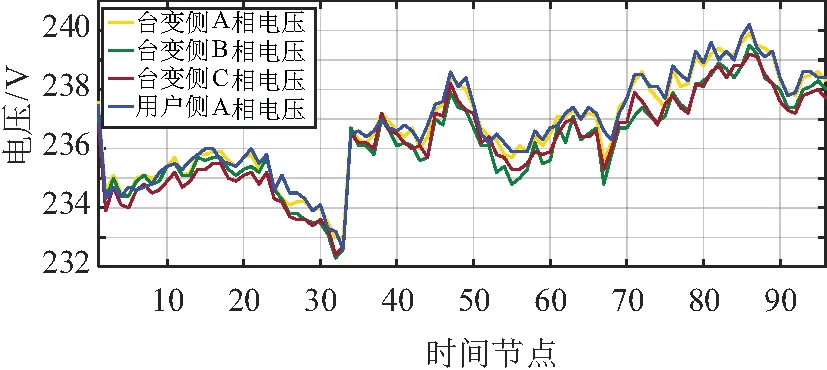
图3 台区内节点日分相电压分布曲线Fig.3 Daily phase voltage distribution curve of nodes in the station

台区内拓扑等效电路[11-12]为如图4所示。

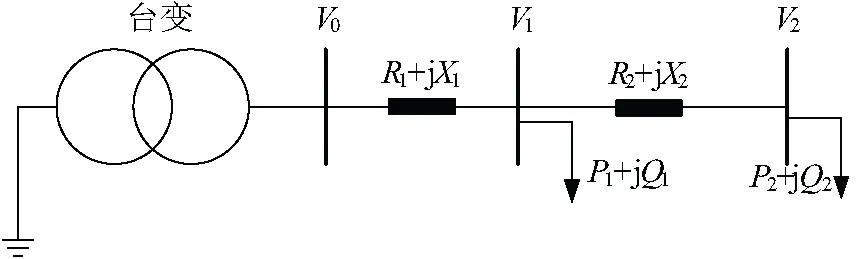
图4 台区拓扑等效电路Fig.4 Station topology equivalent circuit

根据线路结构可得到电压关系函数如式(1)所示：

(1)

其中：

(2)

(3)

(4)

(5)

可见呈现辐射式结构的台区首末端电压呈现递减趋势，递减程度与居民用户的使用负荷大小相关。当台区间的电压相似性过大，而用户侧的负荷大到导致首末端电压差距过大时，仅从电压的相似性进行台区的区分难度较大[13]。

2 基于Hausdroff距离的户变及相位识别分析

2.1 Hausdroff距离算法应用可行性

Hausdorff 距离算法是一种快速波形相似度比较算法，是描述两点集之间相似程度的一种量度，它是两个点集之间距离的一种定义形式，在医学病理诊断方面得到了广泛应用。

根据前节分析，不同台变的电压一般存在明显的差异性，而同台区同相位节点呈现明显的电压相似性，可通过电压相似性进行户变关系和相位关系的识别，同时电压相似性不存在曲线压缩和拉伸的情况，存在相似性的同一台区或同相线路其电压相似主要表现为电压的纵向值的差异，而Hausdroff距离正是表达一种曲线的最大差异值。相对于传统的基于皮尔逊相关系数进行相似度比较方法，Hausdroff距离在时钟不同步问题时更具优势，因此选用Hausdroff距离进行电压相似性分析，并进一步实现台区和相位的识别是合适的。

2.2 基于Hausdroff距离的识别基本判据

根据Hausdroff距离的设定原理，首先设定各待识别的末端节点电压曲线点集Vbottom(i)，以及目标台区台变侧电压曲线点集Vtrans(j)，i和j均为节点电压编号。

Vbottom(i)={u1(i),u2(i),...,un(i)}

(6)

Vtrans(j)={u1(j),u2(j),...,un(j)}

(7)

由此可得到每个待识别的末端节点电压曲线点集与已知目标台区台变侧电压曲线点集之间的Hausdroff距离为：

(8)

其中：

(9)

(10)

则待识别的末端节点i最相似的台区节点电压编号为：

ID(i)=J|H(Vbottom(i),Vtrans(J))=min{H(Vbottom(i),Vtrans(j))}

(11)

式中J所属的台区即为末端节点i所属台区，J所属的相位即为末端节点i所属相位。

设定准确率的判断原则为：

(12)

式中cIdentify(i)为识别为某台区某相(编号为i)的数量；cTrue(i)为其中正确判定结果的数量。

根据以上判定原则应用到图2的三条电压曲线中，分析Hausdorff距离能否实现同台区与相邻台区户变关系的有效鉴别，得到用户侧电压曲线与台区1与台区2台变侧电压曲线的Hausdorff距离分别为2.488 0和3.371 9，根据判定原则，更小Hausdorff距离指向了正确的台区编号。

应用到图3所示的四条电压曲线中，分析Hausdorff 距离能否实现同台区内相位有效鉴别，得到用户侧电压曲线与台区A、B、C三相电压曲线的Hausdorff距离分别为2.488 0、6.629 5、6.331 7，同样根据判定原则，更小Hausdorff距离指向了正确的台区和相位编号。

但是实际分析数据中也存在一部分的识别指向了错误的结果，考虑是因为当用户侧的负荷过大导致首末端电压相差较大时，仅从电压的相似性进行台区的区分难度变大；另一方面存在的数据异常点也会影响识别的可靠性，因此需要对整个识别流程进行优化设计，以提高识别的准确率。

3 基于Hausdroff距离算法的识别流程设计

根据基于Hausdroff距离的拓扑识别基本判据和初步应用分析，识别流程的优化设计包括以下几个方面：

(1)考虑到仅从一天数据进行分析，可能存在电压异常点，进而导致Hausdorff距离因误差而过大，可利用多日的数据设计滑动窗口，构建多个小的对比波形，进行综合分析得到最终结果；

(2)根据电压相似性分析，末端用户负荷过大引起首末端电压差过大，影响相邻台区用户的有效鉴别，可通过在电压点集中剔除电流过大时间点的电压，然后再进行比较；

(3)可对优化的待评判数据集，应用基于Hausdroff距离的拓扑识别基本判据实现户变关系、相位匹配识别。

综上，设计基于Hausdroff距离算法的识别流程如图5所示。

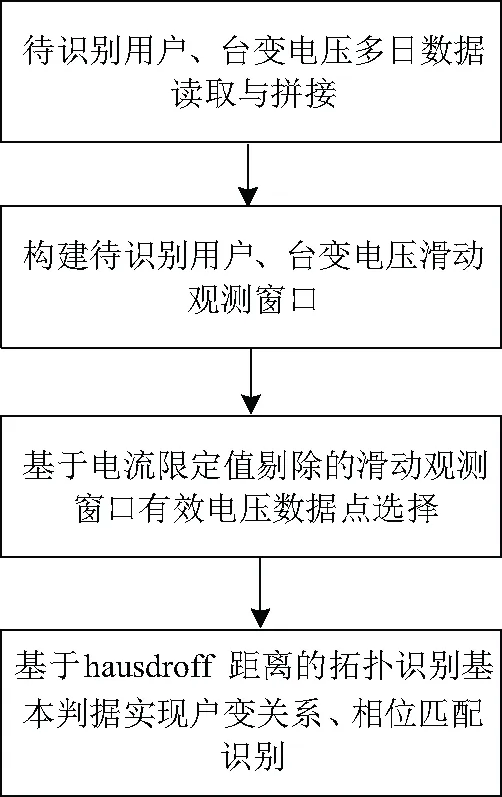
图5 基于Hausdroff距离算法的识别流程Fig.5 Recognition framework based on the Hausdroff distance algorithm

4 识别流程中的数据集优化方法设计

针对识别流程中滑动观测窗口构建和有限电压数据点选择的具体方法如下所述。

4.1 滑动时间窗电压数据集滚动匹配

在已获得的待归类末端用户节点数据集Vbottom(i)和目标台区台变侧电压曲线点集Vtrans(j)中设定滑动时间窗口m，窗口时间间隔为ω，窗口内观测点分别为Sω(Vb(m))和Sω(Vs(m))：

Sω(Vb(m))={ub(m-ω),ub(m-ω+1),...,ub(m-1)}|ub∈Vbottom(i)

(13)

Sω(Vs(m))={us(m-ω),us(m-ω+1),...,us(m-1)}|us∈Vbottom(i)

(14)

可将窗口内数据应用基于hausdroff距离的拓扑识别基本判据后，得到每个末端用户多个滑动窗口的最终结果，取出现频次最多的结果为目标结果。

4.2 基于电流限定的电压数据筛选

在4.1基础上，对窗口内观测点Sω(Vb(m))和Sω(Vs(m))进一步处理得到Sω′(Vb(m))和Sω′(Vs(m))：

Sω′(Vb(m))=Sω(Vb(m))|is(m)

(15)

Sω′(Vs(m))=Sω(Vs(m))|is(m)

(16)

其中Iset为判定的电流过大的限定值，从而实现观测数据点的进一步限定和筛选[14-15]。

5 案例应用与分析

为验证文中所述方案的有效性，从AMI中抽取含949户的10个台区三日数据进行应用分析。

直接选择三天中的一天不经任何数据优化处理，应用识别基本判据，户变关系识别平均准确率可达76.3%，相位识别的平均准确率可达73.85%，超过半数的台区拓扑和相位准确率达90%以上，多个台区准确率可达100%。准确率低的台区因为相邻台区电压相似程度高的原因导致。

图6是已识别的某台区A相所有用户的电压波形。

图6 已识别的同台区同相所有用户的日电压波形Fig.6 Daily voltage waveform of all users identified in the same phase of the same station area

可以从图6曲线中看出，该30个用户与该台区A相位电压曲线呈现一致性，从而实现相位和户变关系的有效识别。

而按照识别流程，对前述的10个台区三天数据进行拼接，得到96*3个点的数据。为构建滑动观测窗口，按步长不断调整窗口时间间隔，不进行电压数据筛选，分别计算10个台区的户变关系和相位平均准确率，得到曲线如图7所示。

图7 不同滑动窗口间隔准确率曲线Fig.7 Accuracy rate curves of different sliding window intervals

可见在滑动窗口为80个点时，户变关系准确率达到85.29%，相位准确率达到77.73%。滑动窗口间隔点数大于或小于80点时，则准确率会降低，考虑造成这种现象的原因为窗口时间间隔过小将导致无法形成有效的对比，过大则无法构建足够的样本完成误差点的排它性过滤。

在滑动窗口间隔设定为80点进行电压数据集选定的基础上，进一步剔除电流过大节点的电压数据后应用相似性判据，实现户变关系准确率达到86.19%，相位准确率达到78.13%，进一步提升了识别准确率。

直接选择一天应用识别基本判据(方法一)、基于滑动窗口滚动匹配(方法二)、基于滑动窗口和电压筛选的滚动匹配(方法三)以及传统皮尔逊系数比较方法(方法四)的详细结果如表1所示。

表1 不同方法下典型台区相位和户变关系识别准确率Tab.1 Identification accuracy rate of phase and household variable relation in typical station area obtained by different methods

通过实例证明通过文中所有的户变关系和相位识别流程可以具备较好的户变关系和相位识别准确率，且相对于基本判据的直接应用通过数据集优化可对识别准确率起到明显的提升作用。同时相对于传统的皮尔逊相关性比较方法，能够提升匹配准确率。

6 结束语

文章从台区电压相似性的角度，应用Hausdorff 距离算法，进行了基于节点电压相似性评估的低压配电网户变关系和相位识别技术研究。

首先面向AMI获取的96点电压数据，分析了通过电压相似性判断和基于Hausdorff距离算法进行户变关系和相位识别的可行性；进而确定了基于Hausdroff距离算法的识别流程，设计了识别基本判据和包括构建滑动窗口和选择有效电压的数据集优化方法；最后通过实际的案例，经过识别方案的不断优化，实现户变关系和相位识别率分别有效提升至86%和78%以上，验证了文章所提方案的有效性，可为低压配电网拓扑识别提供参考。