基于Ansys的高压输电塔风振特性分析

耿贞伟，苏文伟，于凤荣，钱晶

(1.云南电网有限责任公司信息中心，昆明 650041； 2.昆明理工大学 冶金与能源工程学院，昆明 650093)

0 引 言

随着西电东输等大型电力工程的稳步推进，电力能源在全国范围内均得到了更大范围的应用。特高压输电塔是电力传输系统中的最重要的部件之一，其维修维护难度大，成本高，因此分析其可靠性和安全性至关重要。过去常用的低电压线路已难以满足日益增长的经济需求，相比之下特高压输电线路能够创造更大的经济效益。对这类架空输电线路，尤其是特高压输电线路来说，由于输电量和工作电压均有大幅提升，电气间隙和多分裂的导线截面积都会增加。这一特点不仅为塔身及塔臂带来了更多负荷，同时也导致在塔—线耦合这个体系中，塔与线二者振动的相互影响已无法忽略[1-6]。

统计表明，输电塔坍塌事故主要是由风振导致的，李宏男等研究了电力塔在多种激励下的动力学特性，并综述了电力塔的安全评估体系。文献[7-8]提出了电力塔的多质点简化模型，在多质点模型中，将导线与塔身等效为利用刚性杆件连接的多个质点模型，并利用该理论模型计算了典型塔的振动特性。文献[9]利用多波屈曲单元对电塔进行理论分析，有效预测了输电塔结构的抗风极限载荷。文献[10]对1 100 kV特高压长悬臂输电塔—线耦合体系的风震特性进行了分析，并得出了悬臂长度对稳定性影响的定性分析结果。目前的研究集中在风振响应或塔本身的振动特性上[11]，因此本文中对风振响应和耐张塔的振动特性进行联合分析具有一定的工程价值与意义[12-14]。

本文综合考虑了现有的电力塔建模方法，利用ansys有限元软件建立梁与杆的混合模型。由于要建立塔—线耦合的模型，进一步使用了悬链法对导线与地线进行几何找形，同时合理地处理塔线耦合的边界条件。最终建立了两塔三线的耦合有限元模型，并对两塔三线的简化模型进行了振动特性的理论分析。在得到振动特性的基础上，又利用有限元动力时程分析方法，进一步分析了塔—线耦合体系的风振响应。

1 两塔三线耦合体系振动特性理论

对一个多塔、线耦合的体系，通常选用一塔两线的分析方法，这样既可以简化模型，又能得到相对精确的结果。但相比于一塔两线模型，两塔三线模型不仅能反映塔—线耦合特性与线—线耦合特性，还能反映塔—塔耦合特性，因此本文选择两塔三线模型进行研究。两塔三线模型如图1 所示[15]，其中EtIt是塔的抗弯刚度，ElIl是导线的抗弯刚度。由于电塔的跨度较大，边界条件变得模糊，因此导线的边界约束对整体的影响可以忽略，简化模型中没有考虑绝缘子等连接部件[11]。

图1 两塔三线耦合简化模型Fig.1 Two-column three-wire coupling simplified model

对于图1所示的系统，采用模态综合分析法分析塔振动与线振动相耦合的动力特性，塔的固定截面主模态与约束模态可分别表示为[16]：

(1)

式中H表示塔身总高；z代表沿塔身高度。

三根长为l的导线的固定截面主模态和约束模态可表示为：

(2)

式中x1、x2、x3、x4分别为图1中标注的沿导线长度。

以式(2)为基础可以得到塔的横向位移：

(3)

同理也可以得到三根导线的面外位移：

(4)

式中φi(t)是广义坐标。

子部件之间相互的位移关系满足：

(5)

因此可得力协调条件:

(6)

可以进一步得到：

(7)

本方法中我们将导线等效为受张力的梁，抗弯刚度可等效为：

(8)

式中i是载荷的角标；l是导线长度；d是导线直径；A是导线横截面积。通过式(9)，可以将阻尼系数化简为：

(9)

综合式(9)，塔—线耦合运动系统的张量表达式为：

Mφ+Kφ=0

(10)

φ=Uφ

(11)

其中的转置矩阵U为：

(12)

因此式(10)转换为：

(13)

(14)

其中元素分别为：

(15)

(16)

式中i为模态的阶数。塔线耦合系统的振动圆频率k可以利用下式计算：

(17)

得到φ的特征向量后，将特征向量代入式(11)可以得到φ的模态向量，综合式(1)～式(4)，可以得到总耦合体系的振动模态。

2 单塔的风速响应谱分析

为了进一步验证所建立的两塔三线模型的合理性，首先对单塔模型进行了风速响应谱分析。

2.1 单塔有限元模型

用于分析模态及塔身受力状况的线框模型如图2所示，许多复杂结构简化为了桁架形式。塔高57 m，呼高29.8 m，结构尺寸由下至上线性变化，根开为8.5 m。结构主要使用的材料是角钢，材料型号选用Q235，Q345两种。为了合理计算电力塔结构，主材等重要部件使用B31梁单元，其余辅材使用T3D2杆单元，在Ansys中赋予角钢截面后的有限元模型如图3所示。

图2 单塔线框模型Fig.2 Single tower wireframe model

图3 单塔有限元模型Fig.3 Finite element model of single tower

2.2 单塔风速响应谱分析

根据现有的大量对风的记录，脉动风可作为一个高斯平稳过程来考察[17]。本文中使用常用的Davenport风速谱对脉动风速进行模拟[18-19]：

(18)

由于Davenport风速谱与高度无关，所以引入一个随机函数来反映不同高度下的风速脉动，此函数的均值为0，任意两点间的互相关函数定义为：

(19)

式中z2，z1分别为两点的高度。

这里引入高度是为了方便在有限元软件中对不同位点施加载荷。模拟总时长为1 800 s，时间增量0.1 s，风速24.5 m/s，地面粗糙度系数0.005，通过上述分析可得到各节点处的脉动风速，图4以塔顶节点处风速即高度57 m风速为例展示了计算结果。同时也可得到风速功率谱密度，以塔顶节点处的风速功率谱密度为例，如图5所示，模拟出的Davenport风速谱与目标模拟谱基本一致，自功率谱的能量分布与实际情况在趋势上一致，数值上接近，说明模拟出的Davenport风速谱是真实可用的。

图4 风速时程曲线Fig.4 Time-history curve of wind speed

图5 风速功率谱密度Fig.5 Wind speed power spectral density

为了避免使用fluent带来的复杂计算流程，本文将塔顶的风速转换为风对塔身不同位点的等效载荷，这里使用标准风压公式：

(20)

式中r表示空气的重度；r=ρ空气·g；v表示风速。结合脉动风压、塔的形体系数、风投影面宽，可以进一步得到各节点处的风载荷。

以图4风速时程曲线为例，进一步将风速转换为塔顶的风载荷，结果如图6所示。

图6 风载荷时程曲线Fig.6 Wind load time history curve

2.3 单塔的风致响应分析

在Ansys软件中定义水平风载荷，将上面得到的载荷施加到各节点上，以分析塔身在耦合体系中的节点位移变化规律。载荷时程曲线如图6所示，以塔顶位节点移情况为例，可得到各节点处位移，如图7所示。

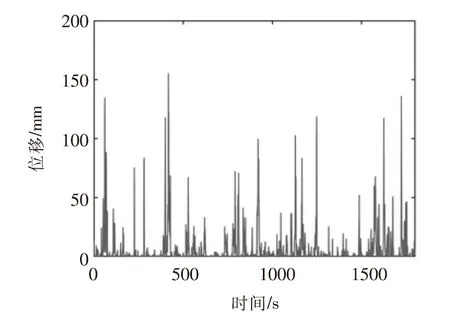
图7 塔顶节点位移曲线Fig.7 Top node displacement curve

根据图6、图7的结果，数值符合预期，证明单塔模型的建立是合理有效的，可以进行下一步耦合模型的分析与建立。

3 塔-线耦合有限元模型

由于导线属于柔性体，在重力作用下形成自然下垂的形状，建立耦合模型就需要寻找该状态下导线的精确几何外形。针对这类问题，我们常用悬链线法进行计算，图8给出了典型的悬链线问题。A,B分别为固定端，O是下垂的最低点，以O为原点建立标准x,y坐标系，定义A, B坐标分别为(xA,yA)，(xB,yB)，A, B两点间的水平距离为D。

图8 悬链线图示Fig.8 Catenary diagram

悬链法的找形方程为：

(21)

式中μ为悬链线系数。该系数可以利用下式计算：

(22)

可以积分得出悬链线长度：

(23)

塔线耦合模型中还需要考虑线与塔之间如何连接，本文中将绝缘子视为刚体，绝缘子与导线间使用关节(Joint)连接，即该节点拥有三个转动自由度，如图9所示。导线的单元定义为梁单元B31，固定边界定义为塔底四角与架空导线的两端。为了使得仿真结果与实际情况更加贴合，建立了三线两塔双回路模型，塔距取典型值400 m，导线与地线型号分别为GLGJ-38/19, GLGJ-16/19，最终的有限元模型如图10所示。

图9 绝缘子模型Fig.9 Insulator model

图10 三线两塔有限元模型Fig.10 Three-wire two-column finite element model

4 塔的风致响应和振动特性分析

4.1 单塔振动特性分析

单塔前十阶振型的有限元计算结果如表1所示，其中一阶振型和二阶振型分别是垂直于导线和平行于导线的两个方向，这两个振型的频率在数值上十分接近。

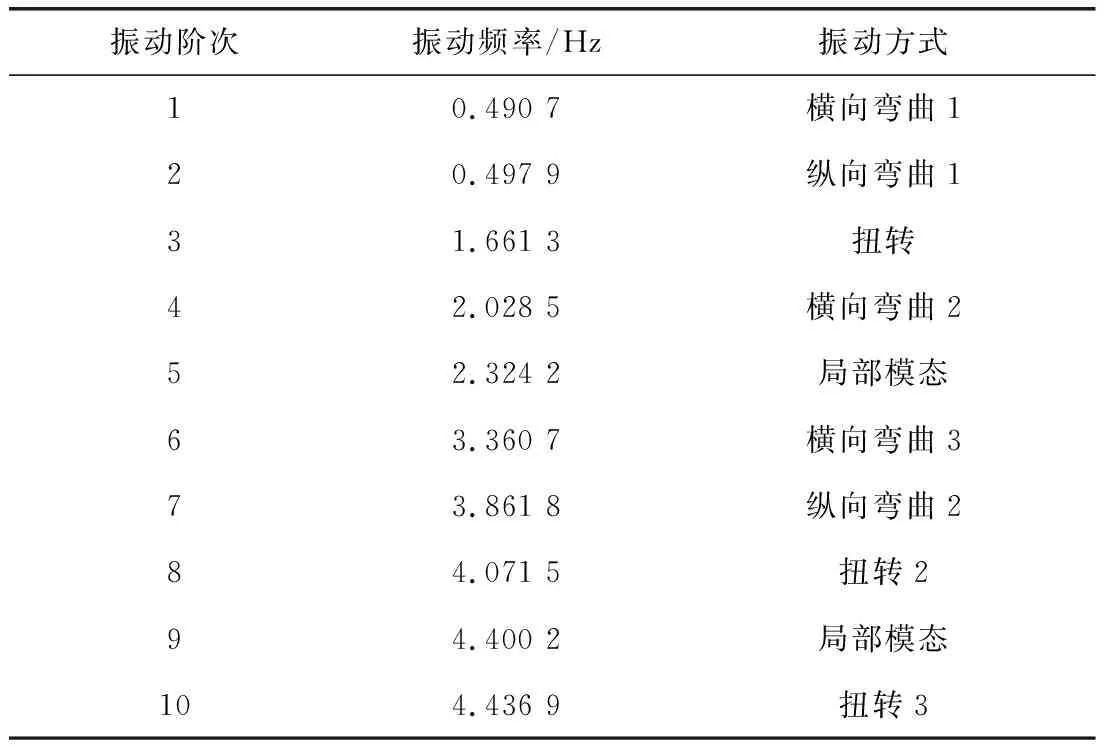
表1 单塔振动特性Tab.1 Vibration characteristics of single tower

4.2 塔-线耦合体系振动特性分析

由于导线属于细长的柔性体，固有频率很低，且各个模态的振型与频率差别很小，因此频率的分布相当集中。在本算例中，我们共计算了前1 000阶模态，并选取了部分塔-线耦合的典型模态进行了说明。

根据有限元的计算结果，塔线耦合体系中绝大多数振型都是导线的振型，且相比于单塔的情况，耦合系统的基频要更低，这也是因为导线的影响。例如前50阶模态频率主要分布在0.01 Hz，0.022 Hz，0.037 Hz，0.047 Hz附近，这是由于建模时考虑到实际条件，因此每根导线并不完全一致，尺寸在悬链线找形方程的附近有一定的浮动，因此每一根导线的振动频率都有细微差别。这四个频率分别是导线的水平一阶、二阶模态，以及垂直方向上的一阶、二阶模态。

表2括号中的反代表两座塔振动方向相反，结合单塔的振动特性，可以直观地看出83与84阶是在线的影响下，两塔具有的共同耦合模态，频率略低于单塔的弯曲固有频率(约0.497 Hz)。487阶是个较为特殊的振型，首次出现了竖直振动的方式，如图11所示。这在单塔的模态分析中是没有出现的，因此这个模态是因为导线在竖直方向上振动而诱发的特殊模态。

图11 487阶模态振型Fig.11 Mode 487-order

表2 塔-线耦合振动特性Tab.2 Vibration characteristics of tower-line coupling

为了验证理论的正确性，依据第二节中的近似理论计算了一阶塔与线的1，2，5，10，12阶耦合理论值，如表3所示。

表3 塔线耦合体系振动频率理论值Tab.3 Theoretical values of vibration frequency of the tower line coupling system

表3展示了近似计算理论反映的塔线耦合体系的趋势。低阶耦合状态下，系统的频率高于单塔频率，随着耦合模态阶数升高，频率逐渐趋于一个最小值，该最小值与有限元得到的塔线耦合体系的频率很接近(0.490 5 Hz)，对应耦合状态下的83,84阶振型，证明了理论切实反映了塔线耦合体系具有的物理特性。

5 结束语

推导了三线两塔耦合系统的简化动力学方程，并利用Ansys软件建立了典型500 kV高压耐张塔的线框模型，利用Ansys有限元软件对耦合系统的振动特性和风致响应特性做了分析，最终得出以下结论：

(1)由于导线在本模型中是跨度极大(相对于导线尺寸)的柔性体，因此导线的振动特性对边界条件不敏感，在本算例中，导线的边界条件不论限制或不限制转动自由度，有限元得到的结果基本一致；

(2)单塔的一阶模态(0.490 7 Hz)与二阶模态(0.497 9 Hz)十分接近，因此耐张塔在横向和纵向上的弯曲刚度基本一致；

(3)耦合后模型的振型、频率与耦合前只有极少数不同，在分析的1 000阶模态中，绝大多数都是塔与线各自的振型，特殊的487阶竖直振型由导线引发；

(4)耦合系统的低阶模态多为耦合共同模态，高阶模态多为诱发模态。双耐张塔的同阶共振有时会出现相反的情况，同阶下，耦合系统的频率要低于单塔频率，主要是由于导线的影响。

最终的理论计算结果与有限元得到的仿真结果基本一致，证明了近似理论算法较为准确地描述了耦合系统的物理特性。