银行所得税和存款保险价格①
明 雷, 唐 慧, 杨胜刚, 黄远标
(1. 湖南大学金融与统计学院, 长沙 410079; 2. 湖南大学工商管理学院, 长沙 410082;3. 湖南大学金融发展与信用管理研究中心, 长沙 410082; 4. 南开大学金融学院, 天津 300350)
0 引 言
2019年5月包商银行被接管的同一天,我国存款保险基金公司成立.这是继2015年实施《存款保险条例》后,我国存款保险制度不断完善的又一重要里程碑.存款保险制度自实施起,在保护存款人权益、增强公众信心以及强化风险约束方面发挥了重要作用,有效维护了银行体系的稳定运行.
当前我国银行体系相对稳定,但潜在风险加剧.一方面,现阶段我国经济面临着需求收缩、供给冲击和预期减弱三重压力,经济将在一段时间内处于下行周期,经济不确定性正在上升.另一方面,中美贸易争端、新冠疫情常态化和俄乌冲突等内外部事件,导致了金融运行环境的不稳定因素在增加.其中,中央政府自2018年以来就出台了一系列对实体企业减税降费的政策,以对冲经济下行风险.据统计,仅2019年全年就减税降费约2万亿元人民币,拉动全年GDP增长约0.8个百分点(1)数据来源: 国家统计局..减税降费政策的确减轻了企业负担,强有力地支持了实体企业发展,促进了经济健康发展.但在持续大规模的减税降费后,财政政策陷入了“两难”的境地:一方面,大规模积极的财政政策使得地方政府财政收支状况不断恶化,制约了未来财政政策的发力空间;另一方面,逐渐增大的经济下行压力,又要求财政政策在经济发展中发挥更大的作用(2)数据来源: https://www.sohu.com/a/359143692_120412715,2019-12-08.因此,对实体企业持续地大规模减税降费是不可行的.在稳增长和防风险的双重目标下,对商业银行进行结构性减税无疑是一个两全其美的办法.经测算(3)限于篇幅,具体的测算结果备索.,2019年全国企业所得税税收结构中,商业银行的所得税税收仅占约1/6.这意味着在不考虑其它因素的情形下,同样的减税对于商业银行的作用大约相当于实体企业的5倍.如果对银行部门减税,可以降低商业银行的经营成本,再通过激励相容的机制设计,降低银行向企业提供的融资成本,可以达到比政府直接对企业减税降费更好的效果.原因在于,从操作层面来看银行的风险识别能力和风险控制能力更强,并且对银行的减税具有杠杆效应.换句话说,如果仅从理论上看,对银行减税降费相比对实体企业减税降费,至少有两点好处:一是对银行减税降费可以使政府面临更少的财政压力,政策更具有可持续性;二是更有利于风险的识别和防范.
从银行内部来看,税收成本是商业银行主要的经营成本之一.与缴纳的存款保险费比较,税收成本要高很多.从2015年设立存款保险制度以来到2019年12月,我国存款性银行业金融机构累计缴纳存款保险费连同利息收入仅1 216亿元.与之形成鲜明对比的是,仅中国工商银行2019年一年缴纳税收就达到1 057亿元.如表1所示,银行的税收成本中,所得税的占比明显高于增值税及其他税种.其中,中国工商银行、中国建设银行和中国农业银行所得税的占比连续两年都超过了80%.由此可见,所得税是商业银行税收中最主要的成本.而存款保险制度是金融安全网的主要组成部分,对于维护银行稳定具有重要作用.鉴于此,考虑银行所得税后如何确定存款保险价格?银行所得税税率又如何影响存款保险的价格?本研究将围绕这些问题展开研究.
1 文献述评
存款保险制度核心问题是存款保险定价,Merton最早利用Black-Scholes期权定价模型研究了存款保险定价问题,开创了存款保险定价研究的先河[1].在Merton的框架下,许多学者进行了拓展研究,将监管检查、监管宽容以及破产成本等引入存款保险定价模型[2-4],或者考虑不同行权方式对存款保险定价的影响[4, 5].Duan在R&V模型的基础上,利用极大似然估计进行了改进[6, 7].国内学者如张金宝和任若恩[8]、李敏波[9]基于R&V模型测算了存款保险费率.近些年来,Lee等用资产相关性来度量银行的系统性风险,并将其引入到Merton模型的框架下,对存款保险进行了定价[10].吕筱宁等[11]将系统性风险、参保比例和逆周期程度系数引入到定价模型,提出基于跨期系统性风险的存款保险逆周期定价方法.明雷等[12]首次将监管惩罚引入存款保险定价模型,研究了监管惩罚和监管宽容对存款保险价格的影响.Camara等[13]考虑了不同保险覆盖(100%覆盖,最大保险覆盖以及有免赔额)下的存款保险定价问题,并以美国的数据进行了实证研究.Merton以及后续拓展研究,本质上是以资产储蓄比和资产波动率来反映银行的风险承担水平,进而对存款保险进行定价.换句话说,已有文献仅考虑了银行自身的风险水平,而忽略了宏观经济政策的作用.然而,宏观经济政策会直接或间接地影响到银行的风险水平,进而影响银行存款保险的价格,这正是本文的研究动机.
近些年来,随着我国减税降费政策持续推进,一些学者开始关注减税降费政策的影响.郭庆旺[14]指出减税降费政策具有持续针对性、成本降低性和长期持久性的特征.减税降费政策是一把双刃剑,其在显著减轻企业负担的同时,也会给各级政府带来巨大财政压力.陈小亮[15]则从人口老龄化的角度说明未来财政负担加重会导致减税降费难度加大.除此之外,还有部分学者关注减税降费对企业行为、地区经济增长、分工和收入分配等的影响[16-19].还有一些学者研究了减税降费政策存在的主要问题、成因及路径选择.杨灿明[20]指出制约减税降费政策进一步深化的原因在于分税制财政体制改革滞后、税收法定原则未落实等,本研究认为有效的应对措施之一是适当降低一些关键税种的税率如企业所得税.邓磊等[21]通过实证研究表明,与增值税、社会保障金相比,企业所得税对经济增长的促进效果最明显.张斌[22]的研究表明,与美国21%的企业所得税税率相比,我国企业所得税税率偏高,应考虑针对不同企业和地区进行结构性减税.一些学者还对新一轮减税降费的实施路径进行了分析[23, 24].王业斌和许雪芳[25]结合中国小微企业调查(CMES)数据,实证分析了减税降费对小微企业劳动生产率造成的影响,发现小微企业面临的实际税费负担与其劳动生产率之间存在着显著的负相关关系,减税降费能有效提高小微企业的劳动生产率.李明等[26]利用“准自然实验”研究了我国税率波动的经济效应,他们认为降低所得税税率有助于企业成长.
通过梳理现有文献不难发现,现有研究忽略了减税降费政策对金融机构的影响.从目前政策来看,我国减税降费政策的着力点是实体企业,而忽视了金融行业特别是商业银行的减税降费.与已有研究不同的是,本研究考虑了银行所得税对存款保险价格的影响.可能的贡献是:第一,研究视角独特,首次将银行所得税引入到存款保险定价模型,将Merton[2],明雷等[12]进行了拓展,得到了存款保险价格的解析解,丰富了存款保险定价理论.第二,分析了银行所得税对存款保险费率的影响,通过比较静态分析发现:存款保险费率与银行所得税税率呈正向关系,即所得税税率越低,每单位存款的保费就越低,从而验证了减税降费的积极作用.第三,在存款保险定价和数值分析的基础上,分别构建回归方程和理论模型分析了银行所得税税率对存款保险费率的影响机制.机制检验表明:银行所得税税率的提高,会通过提高银行的风险承担水平,进而提高存款保险费率.在当前国内经济持续下行、外部经济政策不确定性增强,以及潜在金融风险不断提高的背景下,本研究对进一步推进减税降费政策在商业银行体系落地提供了理论依据和实践参考.
2 考虑银行所得税的存款保险价格
2.1 存款保险定价模型
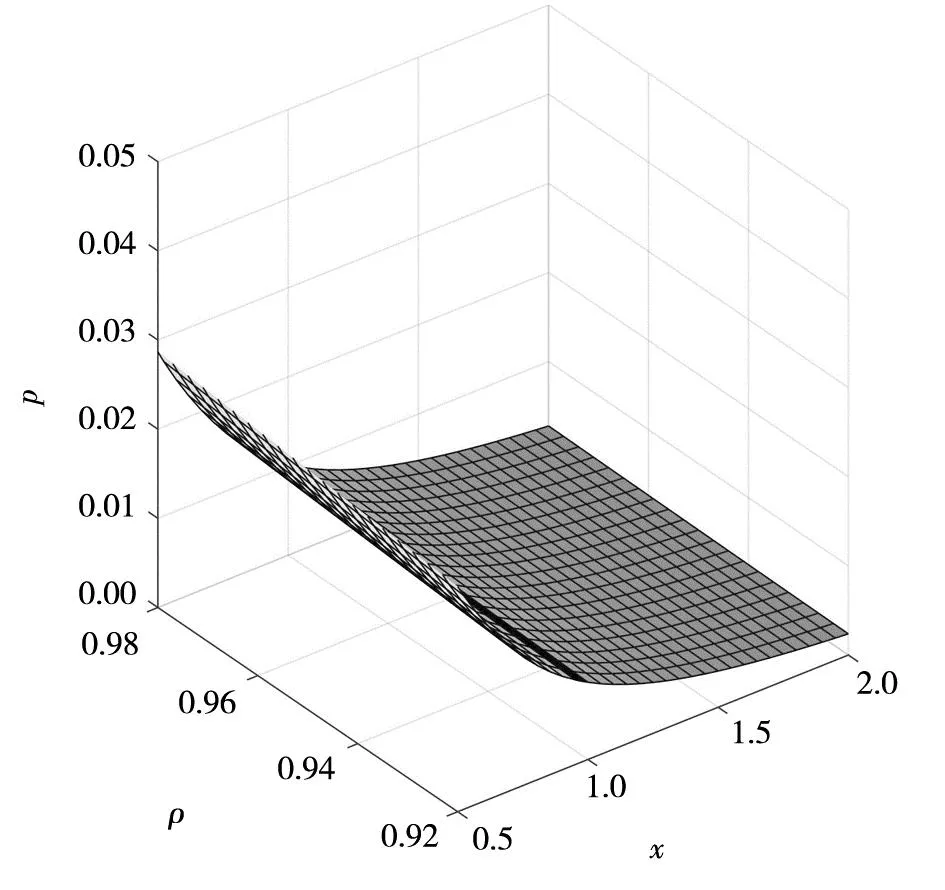
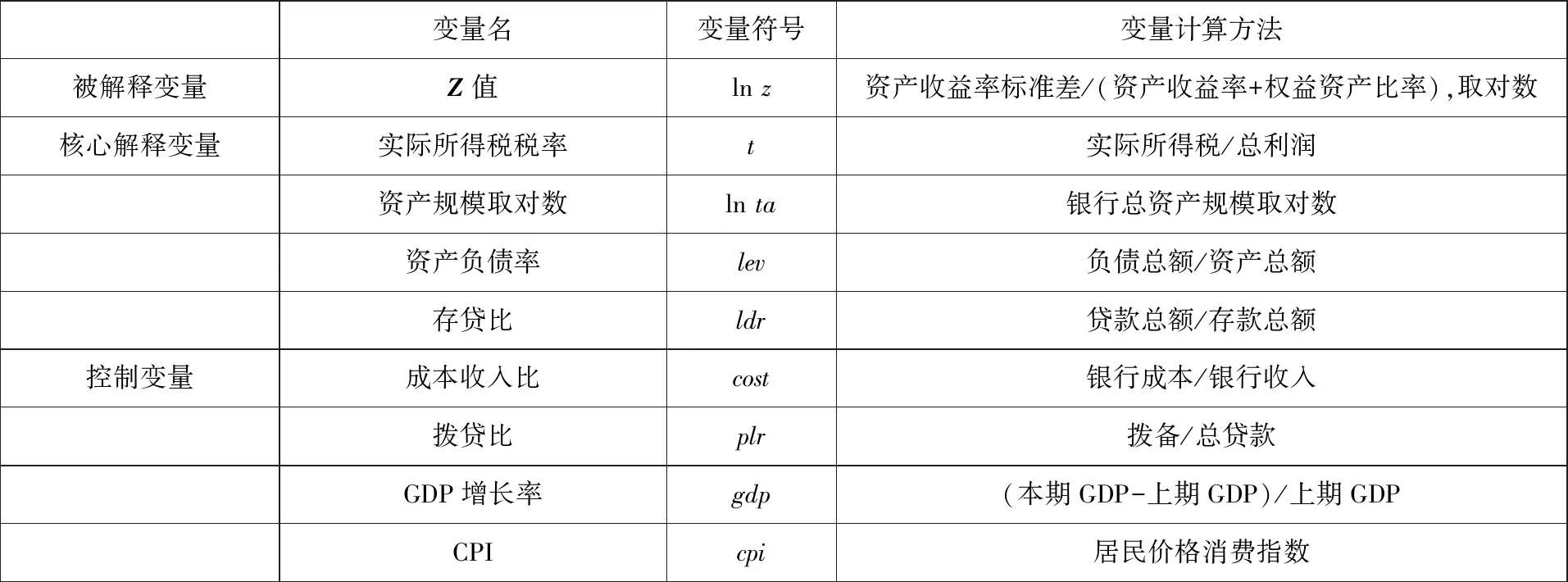
借鉴Merton[2],明雷等[12]的做法,假定dD/dt=gD,其中g为存款增长率.假设存款保险监管机构存在监管宽容,监管宽容系数为ρ.存款保险监管机构对银行进行监管检查,监管检查服从强度为λ的泊松分布,监管检查成本为C.为推理计算方便,假定每单位存款监管检查成本是常数.当银行资产满足V>D时,银行正常经营,那么存款保险机构只需支付监管检查成本C;当银行资产满足ρD 不同于Merton[2],明雷等[12],本研究一个核心假设是将考虑银行所得税对存款保险价格的影响.因此,假设τ为所得税税率,R为税前存款利率,s为税前服务费率,并且存款增长率满足g=(R+s)(1-τ).假定r为税前贷款利率.对于银行而言,要保持银行的盈利性,那么税前贷款利率必须高于税前存款利率与税前服务费率之和,即r≥R+s;否则银行的贷款收益难以抵消银行的成本.考虑银行所得税后,假定银行资产服从以下随机过程dV={αV-[(R+s)(1-τ)-g]D}dt+σVdz,其中α表示税后单位时间资产的期望收益率. 根据以上假定,存款保险费率满足式(1) (1) (2) 式中μ=(r-R-s)(1-τ).上述微分方程组满足以下边界条件,如式(3)所示.其中前4个等式是通常满足的光滑黏贴条件,第5个等式的证明见Merton[2].最后一个等式直观意思是,当资产储蓄比趋于无穷时,单位存款保险费率有界.其经济学含义是,资产远远超过负债(即存款),那么银行就不会出现挤兑风险,因此只需要缴纳有限的保费. (3) 通过推导证明(5)限于篇幅,具体的推导过程备索.,微分方程式(2)在满足边界条件式(3)下的解如式(4)所示 (4) 式(4)给出了考虑银行所得税下的存款保险的价格,其中系数满足式(5) 2.2.1 参数选择 考虑参数实际含义的同时,借鉴现有参考文献,设置如表2所示参数取值.参考大型国有商业银行的一年定期利率和一年期贷款利率,本研究中银行存款利率R取值为2%,银行贷款利率r取值为5%;τ设置为25%,依据是银行法定的企业所得税率;参考银行跨行收取的手续费,银行服务费s取值为0.2%;c表示每单位存款的检查成本,σ表示银行资产波动率,λ表示监管机构对银行检查的强度,三者取值分别为0.000 02,25%,0.002[12];根据已有文献,通常监管宽容系数在[0.9,1]之间[27, 28],本研究取0.95. 表2 模型参数取值 2.2.2 数值分析 图1表示在其他参数不变的情形下,资产储蓄比、银行所得税率与存款保险费率之间的关系.由图1可知,存款保险费率与资产储蓄比呈反方向变动关系,即资产储蓄比越高,每单位存款的保费就越低.这与现有研究结论一致[2, 12],也符合经济学直觉.而存款保险费率与税率呈正向关系,即所得税税率越高,每单位存款的保费就越高.直观来看,银行所得税的提高会增加银行投资风险以及提高银行杠杆率,银行整体风险上升要求更高的存款保险费率.存款保险费率与税率的正向关系进一步确认了减税政策的积极作用,下文将进一步分析背后的机理. 图1 资产储蓄比、 税率对存款保险费率的影响 根据已有文献,通常监管宽容系数为0.95左右,且差异不大.因此,本研究将监管宽容系数设置在[0.92,0.98]区间,来分析资产储蓄比与费率之间的关系,结果如图2所示.在其他条件不变的情况下,监管宽容程度越高(即系数越小),存款保险费率越低.原因在于监管宽容程度越高表明,存款保险监管机构的风险容忍度越高,认为银行破产的概率较小,则单位存款所要求缴纳的保费越少,这符合保险费率厘定的原则.资产储蓄比与费率呈负向关系,与图1的结果一致.表3给出了在其他参数不变的情况下,存款保险费率与监管宽容程度、银行所得税率的关系.结果表明:在同一所得税率下,无论银行资产储蓄比处在什么水平,监管宽容程度越低(即宽容系数越高),银行存款保险费率越高,这与图2的结果相同.而在同一监管宽容程度下,银行存款保险费率随着所得税率的增加而增加,与图1结果保持一致. 图2 资产储蓄比、 监管宽容程度对存款保险费率的影响 表3 监管宽容程度、 银行所得税率与存款保险费率的关 为了分析在不同所得税税率水平下,减税政策对存款保险费率带来的影响,计算存款保险费率关于税率τ的导数.图3给出了存款保险费率关于银行所得税税率变化率与税率及资产储蓄比的关系.通过图3可以看出,存款保险费率关于税率τ的导数始终为正数,并且随τ减小而减小.这就意味着,相同幅度的减税政策,较高的银行所得税税率对存款保险费率的影响要大于较低的银行所得税税率对存款保险费率的影响.换句话说,减税政策对存款保险费率的边际影响会随着税率本身减小而减小;这对政策部门进一步推进减税政策具有重要意义,减税政策的边际作用递减意味着政策实施需要考虑“天花板”. 图3 存款保险费率关于银行所得税税率变化率与税率及资产储蓄比的关系 表4给出了其他条件不变情况下,当单位存款监管成本取值较大时,每单位监管成本、资产储蓄比与存款保险费率之间的关系.根据表4结果可知,存款保险费率随着每单位存款的监管成本上升而增加.对于存款保险监管机构而言,监管成本可以看成发行存款保险这种特定保险产品的一项成本,而存款保险保费是该种保险产品的收入,当保险成本上升时,为了保持收支平衡,应当提高该种保险保费.这就解释了每单位存款监管成本与存款保险费率之间的正向关系.同时由表4可知,不考虑其他因素的影响,存款保险费率与资产储蓄比呈反向变动关系,这与图1和图2所示结果一致. 表4 资产储蓄比、 监管成本与存款保险费率的关系 根据前文存款保险定价模型可得,银行所得税税率与存款保险费率之间存在正相关性关系(正相关III),如图4所示.根据文献[29-31]可知银行风险与存款保险费率之间存在正相关关系(正相关II),因此本研究聚焦于分析银行所得税税率与银行风险之间的关系(正相关I).这里将通过简单的离散模型来分析银行所得税税率与银行风险水平之间的关系. 图4 银行所得税税率影响存款保险费率机制的流程图 表5 两期银行资产负债表 =L0θ+L0rθ+τ(L0r-D0R)θ- (L0+T0-E0)(1+R) =[L0(1+r)θ-L0(1+R)]+[τ(L0r- D0R)θ-T0(1+R)]+E0(1+R) ≥E0(1+R) (6) 根据式(6)可知,随着税率提高,保持所有者权益期望值不变时,银行会选择贷款利率(r)高并且贷款投资成功概率(θ)低的贷款进行投资.换句话说,银行所得税税率的提高会刺激银行进行更加激进的风险投资,导致银行风险承担水平上升.这表明银行所得税税率与银行风险之间存在正相关关系,这与实证检验得出的结论一致. 前文通过一个简单的离散模型,分析了银行所得税税率与银行风险承担之间的关系,接下来通过实证检验,进一步研究银行所得税对银行风险承担水平的影响,以期从另一个角度来分析银行所得税对风险承担的影响. 选取我国50家银行2010年—2019年共10年的数据.其中50家银行中包括:5家国有银行,9家股份制银行,36家城市商业银行.数据来源于Wind、各银行年报以及国家统计局. 参考明雷等[32]、汪莉[33]等的研究,本文构建如方程式(7)所示的实证模型 lnzi,t=β0+β1ti,t+∑λicontroli,t+μi+εi,t (7) 其中下标i表示银行个体,t表示年份,μi为银行个体固定效应,εi,t为随机误差项.lnzi,t为被解释变量,作为银行风险水平的代理变量,该指标值越大表明银行风险承担水平越高.ti,t表示银行实际所得税税率,为核心解释变量,controli,t为控制变量.根据数据可得性,参考明雷等[32]和汪莉[33]的研究,本文从银行层面选取了5个控制变量,分别是资产规模、资产负债率、存贷比、成本收入比和拨贷比.宏观经济层面选取了GDP增长率以及消费价格指数CPI.模型变量具体的计算方法与说明见表6. 表6 实证变量及其说明 表7给出了所有实证变量的描述性统计.其中,银行Z值的均值为1.954 2,标准差为97.23%.实际所得税税率均值为20.96%,小于现有银行法定所得税税率25%,其中最小值仅为3.5%,最大值达到了30.29%.Z值和实际所得税税率标准差数值较大,表明这两组数据在各银行间的差异较大.资产负债率方面,均值为93.29%,与银行负债经营特征相符.存贷比方面,均值为64.93%, 最低的仅为31.19%, 而最高的达到了99.38%, 说明各银行经营差异较大. 拨贷比方面,均值为2.845%,最大值达到了5.127 2%,最小值也有1.309 9%,说明整体的风险抵御能力较强.其中,本研究对所有变量进行两端各1%的缩尾处理,来消除极端值对实证结果的影响. 表7 主要变量描述性统计 表8报告了基准回归结果,这里的被解释变量都是Z值.其中,回归(1)~回归(3)为未加入控制变量,混合OLS、固定效应和随机效应模型估计出的所得税税率对银行风险的净影响.回归(4)~回归(6)为加入控制变量后,混合OLS、固定效应和随机效应模型估计出的所得税税率对银行风险的总影响. 表8 基准回归结果 从表8可以看出,在未控制和控制银行层面和宏观经济因素的回归结果,均显示所得税税率与银行风险承担水平之间存在显著的正向关系.考虑到混合回归、固定效应模型以及随机效应模型的回归系数存在差异,为此进一步利用计量经济学检验方法来识别更有效的回归结果.其中,F检验显示,银行个体虚拟变量是显著的(P值小于0.01),应该拒绝“所有个体虚体变量都为0”的原假设,认为存在个体效应,不应使用混合回归,而该选择个体固定效应回归.豪斯曼检验的P值为0.028 7,远小于0.1临界值,认为固定效应模型的回归结果更优.除了统计学意义上显著外,从经济显著性上衡量(以第(5)列结果为例):银行所得税税率降低1个单位(1%),Z值对数值可以降低2.741 9%,如果与Z值标准差对比,能够解释Z值变动的2.8%(0.027 4/0.972 3),具有较强的经济显著性. 1)替换被解释变量 为了验证实证结果的稳健性,本研究通过改变被解释变量度量方式进一步检验.将银行风险承担的代理变量改为资产收益率波动率(ROAV)和不良贷款率(NPL),控制变量与前文一致,对变换被解释变量后的模型进行重新估计.回归结果见表9,豪斯曼检验结果显示,被解释变量为收益率波动率(ROAV)的模型应选择随机效应模型估计结果,不良贷款率(NPL)的模型应选择固定效应模型估计结果.具体的回归结果显示:在1%的显著性水平下,实际所得税税率与银行风险水平之间存在显著的正向关系.说明替换被解释变量之后本研究的结论仍然是稳健的. 表9 替换被解释变量 2)控制遗漏变量 使用固定效应模型进行估计一定程度上可以缓解遗漏变量导致的内生性问题,为进一步缓解可能存在的遗漏变量内生性问题,本研究在基准回归模型基础上进一步增加了银行层面和宏观层面其他可能的遗漏变量.具体包括:净资产收益率(roe)、银行业14t同业拆借利率(rate)和货币供应M2增速(m2gr).回归结果如表10所示,实际所得税税率与银行风险水平仍然在5%水平下显著为正,仍然符合本研究假设. 表10 遗漏变量问题 3)互为因果内生性问题 从银行所得税税率和银行风险承担的互动逻辑来看,银行的所得税税率由政府部门制定,相对银行风险承担而言是较为外生的,因此银行风险承担水平对银行所得税税率的反向因果效应较弱.但是,为了进一步缓解可能存在的互为因果内生性问题,本研究尝试利用滞后期、工具变量和GMM方法重新估计假设. 首先,采用滞后一期的银行实际所得税税率重新估计结果,采用滞后一期的银行实际所得税税率可以一定程度上缓解互为因果的内生性问题,因为当期的银行风险水平一般不会影响上一期的银行实际所得税税率.表11中回归(1)~回归(3)报告了实际所得税税率滞后一期的回归结果,显示实际所得税税率仍然在1%水平下对银行风险承担显著为正. 表11 内生性问题 其次,尝试寻找合适的工具变量进行2SLS估计,但是目前的研究缺乏合适的工具变量,本研究尝试使用上一期的所得税税率和同类型银行所得税税率均值作为各银行实际所得税税率的工具变量重新进行估计.回归结果见表11中的回归(4)和回归(5),一阶段回归中,两个工具变量对银行实际所得税税率影响显著为正,说明本研究工具变量选取较为合理.二阶段回归中,银行实际所得税税率对银行风险仍然在1%水平下显著为正.工具变量的相关检验均显示工具变量不存在弱工具变量、识别不足和过度识别问题. 最后,利用GMM方法重新估计本研究的假设,回归结果见表12.其中回归(1)~回归(2)为差分GMM的估计结果,回归(3)~回归(4)为系统GMM的估计结果.模型设定方面,所有回归的AR(2)和Hansen检验的P值均大于0.1,通过了序列自相关检验和工具变量过度识别检验,说明GMM模型设定合理.所有回归结果均显示,银行实际所得税税率对银行风险仍然在1%水平下显著为正,进一步验证了本研究的假设. 表12 GMM回归结果 本研究在考虑银行所得税的影响后,基于Merton的研究[2],给出了存款保险定价模型.通过比较静态分析发现,银行所得税税率与存款保险价格之间存在正向相关关系,并利用实证回归和理论模型探讨了银行所得税对存款保险价格的影响机制.首先,利用面板数据实证检验了银行所得税税率与银行风险水平之间的正向关系;其次,通过离散模型发现:当银行所得税税率提高时,银行会选择更为激进的投资方案,从而加剧银行风险.研究表明,银行所得税是通过影响银行风险从而进一步影响存款保险价格的. 在当前国内经济形势低迷,新冠肺炎疫情席卷全球之际,“减税降费”作为一项重要的扩张性财政政策,如何更好地与我国国情相结合促进宏观经济平稳运行有待各界关注与研究.2019年我国全年税收收入为157 992亿元,假设银行业所得税税收占比约为17.87%,则银行业所得税收收入约为6 666.7亿元,大致相当于2019年全年减税降费规模的25%.因此,针对银行业进行所得税税制改革,促使银行更好地服务于实体经济显得尤为关键,同时也有助于防范化解银行潜在风险.但是,如何合理地设计银行部门减税政策,在兼顾银行的合理的发展需求的同时,使其发挥降低企业融资成本的关键主体作用,更有效地促进实体经济的发展也是今后需要重点关注和考虑的方向.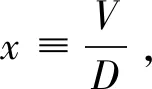

2.2 比较静态分析





2.3 影响机制的一个简单模型




3 银行所得税对银行风险承担水平影响的实证检验
3.1 模型设定与变量说明
3.2 描述性统计

3.3 基准回归

3.4 稳健性和内生性检验




4 结束语

