考虑服务流程信息的服务配置优化方法①

雒兴刚, 刘 伦, 张忠良, 张洪波

(杭州电子科技大学管理学院, 杭州 310018)

0 引 言

世界经济重心正由制造业不断向服务业倾斜,服务业已成为当今世界经济增长的新引擎,因而倍受各国政府的重视.近年来,我国服务业增加值和就业规模也在不断增长,已成为国民经济的第一大产业.2019年我国的服务业增加值534 233亿元,占GDP比重为53.9%,比上年提高0.6个百分点(1)中华人民共和国2019年国民经济和社会发展统计公报, 2020年2月..在互联网和信息技术的支撑下,新的商务模式和服务业态不断涌现,许多传统的产品导向型企业开始转变盈利模式,蜕变为服务导向型企业.

在服务的开发和设计过程中,应对大规模个性化顾客需求的一个重要使能技术是模块化(modularization).服务模块化的基本思路是将服务分解成若干模块,模块之间存在接口,而模块内部包含若干可替换的服务组件[1].服务配置就是将服务模块中的服务组件按一定的方式组合起来,形成可以满足特定顾客需求的服务解决方案.目前服务配置方法已成功应用于物流服务、制造服务、旅游服务、IT服务、医疗服务、金融服务等领域[2].服务模块化的优点主要包括降低费用、提高服务柔性、增强服务可复用性、改善服务标准化、降低系统复杂性等[3].

服务是一种特殊类型产品.不同于实体产品,服务具备无形性、易逝性、异质性、可变性等特征,因此服务模块化无需考虑几何尺寸和物理接口,并且服务模块中的各服务组件不仅存在复杂配置约束,还存在串并行等时序执行关系.因此,服务配置中选择不同服务组件,可能会超过原定服务工期,导致不可行的配置结果.另外,服务在执行过程中需要各类服务资源支持(如人员和设备等),有必要在配置过程中考虑时变服务资源的限制,达到瓶颈资源的合理利用之目的.

本研究旨在解决服务配置过程中的优化问题,具体可描述为:已知服务的模块化结构、流程约束和时变资源约束等,根据顾客需求对预先定义的可配置服务的模块化组件进行组合,为顾客配置到最满意的个性化服务过程.该问题主要包括以下要点:1)在优化模型中需考虑多种优化目标,如最大化顾客需求指数、最小化总服务成本和最小化总服务处理时间等;2)服务配置中需考虑模块化组件之间的相容性关系和排斥性关系;3)在配置优化过程中,需考虑各服务模块之间存在时序关系和时变资源约束.

1 相关研究综述

产品配置的思想起源于20世纪70年代,目前已被广泛应用于计算机、汽车、电梯以及一些机电产品等.产品配置方法根据其知识表达方式和推理机制的不同,通常分为基于特征的配置方法、基于规则的配置方法、基于模型的配置方法、基于本体的配置方法等[4].随着服务科学发展,由产品配置研究延伸出的服务配置研究受到众多学者关注.下面先简要回顾服务模块化的相关文献,再梳理和分析服务配置的最新研究进展.

1.1 服务模块化

服务模块化是改善服务效率的一种有效途径.通过使用模块化技术,服务企业可以更好的利用规模效应和服务资源,从而缓解服务过程的复杂度,起到降低服务成本和增加服务弹性的目的.服务模块化相关文献主要集中于以下几类:1)服务模块化的概念和框架模型[2, 5];2)医疗、旅游、物流、IT服务等几个典型服务领域的案例分析和解释[6-10];3)基于实证分析方法的服务模块化过程的接口和效果评估等[11-13];4)基于设计结构矩阵等方法的服务模块划分方法等[14].这些文献的分类、比较和分析请参见相关综述论文[3, 15, 16].

1.2 服务配置

服务配置的相关文献中,一些研究探讨了服务配置问题的概念、定义和概念模型等.例如,Heiskala等[17]给出服务配置问题的定义,并用统一建模语言提出服务配置的概念模型.Becker等[18]将产品工程的基本概念推及到服务产品,提出采用大规模定制策略来处理服务多样化问题,并建立一种基于规则的框架模型来表示不同的维修服务.Roy等[19]在考虑顾客、生产商和产品生命周期特点的基础上,提出一个产品服务系统的配置框架模型,并提供一个简单应用案例.Legnani等[20]为售后服务配置问题提出一种新框架模型,并结合三种不同类型公司的产品售后服务进行了分析.Mannweiler等[21]提出针对顾客需求为产品服务系统进行配置的一个框架模型,主要包括系统需求采集与分析、产品服务系统的矩阵生成与配置规则表示、顾客订单评估与生成等几部分.Guillon等[22]在对产品和服务配置评估后,构建了一个能够覆盖整个范围和多样性商业报价的基于知识模型,并在实际公司应用中得到验证.Campos等[23]以单顾客需求为驱动,构建了集成模块化产品的配置和可重构制造系统的非线性整数规划模型,最大限度降低大规模定制产品的制造成本,并提供了智能手机制造的案例分析.

和产品配置类似,服务配置也可认为是一类特殊类型的约束满足问题,其中配置约束的复杂程度和表示方法对配置结果影响很大.有许多研究借鉴了产品推荐系统的概念,采用不同知识表示模型来处理配置规则,提出一些基于知识的服务配置方法.例如,Baida等[24]分析了服务和有形产品的不同点,建立了支持模块化结构的服务本体模型,描述了在此模型基础上如何自动生成多种能源服务配置解决方案的案例分析.Jian等[25]提出了一种应用本体表示服务流程结构和知识的服务配置模型,该模型交互性能良好,支持服务内容和服务流程的动态定制.Shen等[26]提出了一种基于人工神经网络的方法,结合RULEX规则提取算法来从历史数据中获得产品配置系统中的配置知识.Dong等[27]构建了基于本体结构化知识的服务产品配置模型,应用语义网规则语言SWRL来表示配置约束,该方法可支持知识的复用和分享,帮助用户发现和配置符合要求的服务产品.Shen等[28]针对产品扩展服务采用网络本体语言OWL来表示配置规则,可以实现顾客需求满足表示、规则推理和结构化知识表达等,并建立了一个基于JESS的决策支持系统.沈瑾等[29]提出应用基于语义网规则语言等来表达结构及规则知识,通过专家系统实现配置方案的推理求解,并提供了楼宇产品服务的案例分析.Wang等[30]基于超图的智能服务系统配置框架,并引入场景信息作为辅助,建立了基于需求属性-产品-服务捆绑-使用场景数据模型的超图模型,更有效的解决了在线3D打印服务的实际问题.Chen等[31]采用新的粗糙模糊数据包络分析获取各模块信息,可以实现混合不确定环境下服务配置,并提供了智能汽车服务的案例分析.

上述基于知识表示的服务配置方法能够表示复杂的配置规则,可通过推理算法生成满足所有配置要求的结果集合,但在处理规模比较大的配置问题时会产生过多的候选服务方案,不利于为顾客进行推荐和选择.针对这一问题,一些研究针对服务配置问题建立了优化模型,以帮助顾客选择最佳的配置方案.例如,Xiong等[32]采用了Petri网结构对网络服务配置问题进行建模,并建立了一个考虑多属性QoS的线性规划模型,其本质属于一种多属性决策问题模型,对于小规模网络服务配置问题非常有效,但没有考虑大规模问题时的候选解集生成过程.Song等[33]针对产品扩展服务建立了一个多目标模型,可为用户提供非支配解集的服务配置方案,并采用一个电梯售后服务的例子进行案例研究.他们的模型适用于服务模块的服务时间独立场景,没有考虑服务流程中模块存在复杂时序约束的情形.Zhang等[34]研究了基于物联网环境的制造服务配置问题,提出采用目标分流法(ATC)处理配置模型的分层次决策目标.但该配置模型的实质是顾客已经确定服务内容后的订单配置,不是以顾客需求的满足程度作为配置目标.Li等[35]为产品服务系统的配置问题建立了一个双层规划模型,其中上层的目标是最大化顾客需求满意度,下层的目标是最大化公司利润.Cui等[36]提出了一种通过主成分分析方法降低客户需求维度和通过量子粒子群优化算法优化内部参数的改进支持向量机模型,用于解决产品服务配置问题.但上述两个文献所构建的模型中没有考虑服务流程因素.

通过上述文献综述可知,服务配置问题已受到学者们的普遍关注,许多相关研究论文借鉴了产品配置的基本理论和方法,例如通过产品服务系统的配置将产品配置扩展到产品和售后服务的组合配置.也有研究考虑了一些特殊行业背景下的服务配置问题,例如医疗服务[37]、物流和软件功能[38]配置问题.但是,对于服务组件之间存在时序关系和服务资源约束这一重要的服务特性,现有的服务配置优化相关文献中都没有在建模过程中予以考虑.

2 基于QFD的多目标服务配置方法

首先定义服务配置问题的一些术语.如图1所示,为了满足顾客的多样化需求,可将服务设计成模块化结构以供顾客选择.服务模块(如M1)中包含若干服务组件(如I11和I12等),这些服务组件功能相似且可以互换,但具体实现、成本、质量等可能有所不同,对应于服务中的某些服务要素.例如,旅游服务可以分成远距交通模块、接站模块、住宿模块、餐食模块、景点模块、购物模块、快递模块等,每个模块中提供不同的服务组件,如远距交通模块中的服务组件可包括飞机头等舱、飞机经济舱、高铁一等座、高铁二等座、列车软卧、列车硬卧等.

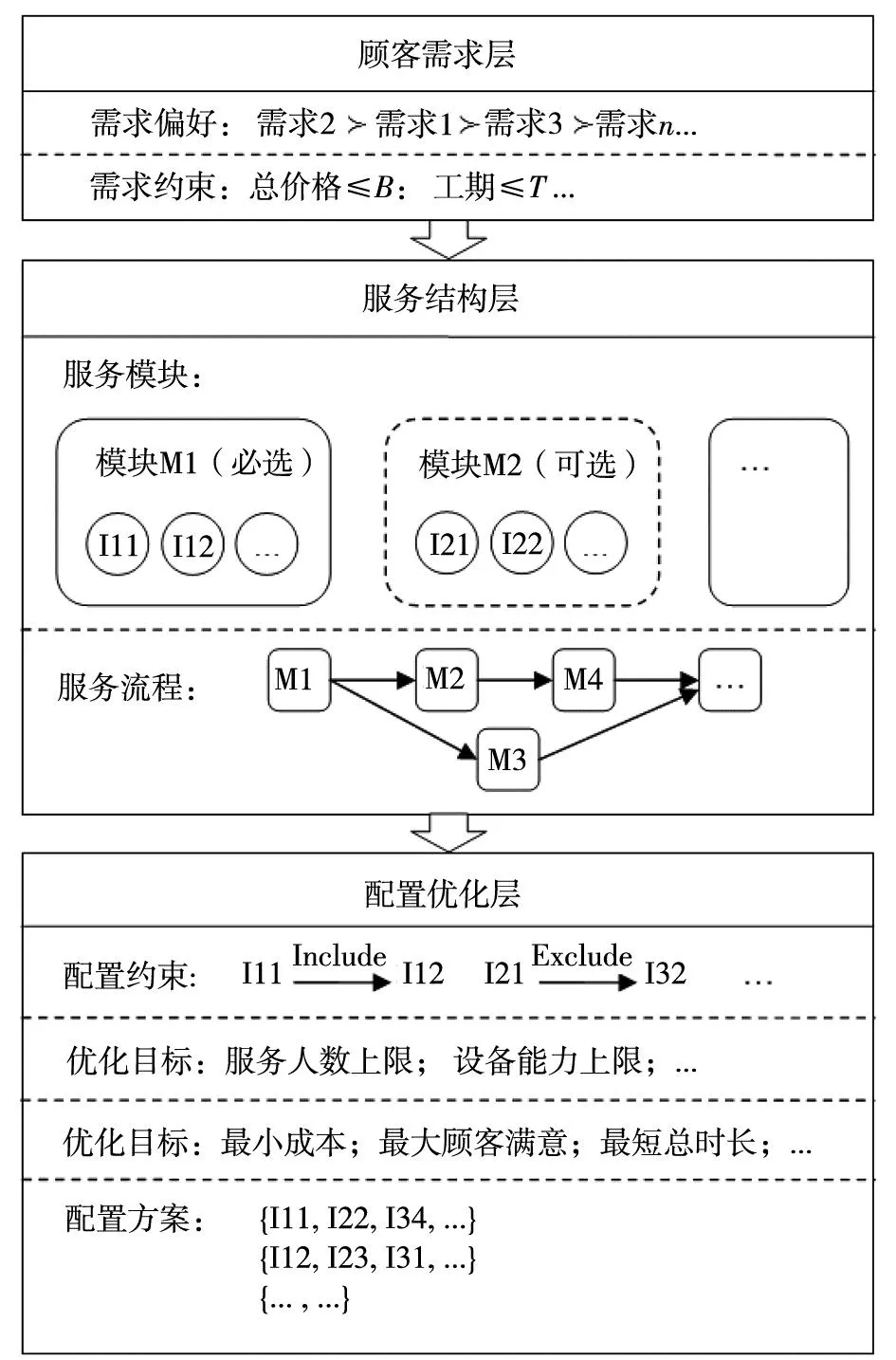
图1 服务的模块化结构和配置

服务模块可以分为两类,一是必选模块(如M1),表示用户在配置服务时必须要从必选模块中选择一个模块组件;二是可选模块(如M2),表示用户可不必从可选模块中选择模块组件.例如,对于一些旅游服务来说,住宿和餐食等是必选模块,购物和一些特殊景点是可选模块.

服务的过程可以通过服务流程来进行描述,在服务流程中服务模块之间可能存在复杂的时序关系.有些服务模块需要另一些服务模块执行完毕才能进行,即服务模块之间的先后序关系.例如,接站服务发生在远距交通服务之后.还有一些服务模块之间并没有时序约束,二者可以并行执行,例如,旅游过程中的餐食服务和快递服务.在一些工程服务中,服务模块之间的关系更加复杂,不但有任务并行和任务串行,而且可能存在服务资源的共享.

在配置过程中,服务模块组件之间可能存在相容关系和排斥关系.配置的相容关系是指当一个模块组件被选中后,另外某个模块组件也一定会被选中.例如,对于某些一日游服务,选择了豪华型轿车,就需选择资深级司机.配置的排斥关系是指当一个模块组件被选中后,另外某个模块组件不可以被选中.例如,选择了某个郊区景点,就不能再选择市中心的餐饮.

顾客的需求偏好信息和需求约束信息是服务配置问题的主要输入,不同的顾客具体要求有所不同.在服务模块化结构的支撑下,考虑服务流程的时序约束和服务组件之间的配置约束,可以选定不同的优化目标建立优化模型,例如最小化服务成本、最小化服务时长、最大化用户满意度等,为顾客提供最优或次优的配置方案.

本研究提出的服务配置方法主要包括以下几个步骤:

步骤1建立服务模块化结构.通过分析服务特征,找到可分解的服务要素,辨析服务要素之间联系,建立服务接口和模块化结构[39].对于服务流程比较复杂的情形,可采用设计结构矩阵(DSM)方法[40]获得高内聚和低耦合的服务模块.定义服务模块中可供选择的服务组件,以及服务组件的基本属性值,如成本和时间等.

步骤2构造两级QFD质量屋.借鉴QFD中产品质量设计的质量屋结构[41],首先建立服务规划质量屋,其中“左墙”是顾客需求,“天花板”是基本服务属性.然后建立模块配置质量屋,其中“左墙”是基本服务属性,“天花板”是各服务模块的服务组件.通过服务的两级质量屋,可将顾客需求的重要性映射到服务模块的服务组件偏好.

步骤3建立多目标服务配置优化模型.在上述两个步骤的基础上,建立服务配置问题的多目标优化模型,综合考虑服务流程的时序约束、服务资源的时变约束、服务组件的配置约束、顾客的服务时间和总预算约束等,具体的数学建模过程请参见第3节的内容.

步骤4根据问题规模应用不同算法求解配置模型.对于中小规模问题,采用空间划分算法来求得多目标模型的精确Pareto解集;对于大规模问题,设计NSGA-II算法可求多目标模型的非支配解集.算法细节请参见第4节的内容.

步骤5解集的缩减和交互选择.针对获得的Pareto解集或非支配解集,首先采用K-means聚类方法确定聚类中心,然后寻找距离聚类中心最近的配置解,将解集缩减到数量比较小的候选解集,最后由顾客进行满意解的目标调整和交互选择.

3 优化模型

3.1 问题描述和假设

设必选服务模块的个数为Nm,每个服务模块中有Ni(i=1,2,…,Nm)个服务模块组件.服务模块组件的服务处理时间和服务单位成本分别表示为tij和cij(i=1,2,…,Nm;j=1,2,…,Ni),服务的固定费用为Cfix,且时间和成本均以整数表示.顾客所要求的总成本预算上限和总服务时间上限分别为CR和TR.

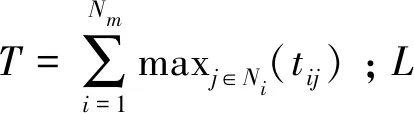
优化问题的主决策变量为xij(i=1,2,…,Nm;j=1,2,…,Ni).如果配置方案中选择第i个服务模块的第j个模块组件,则xij=1;否则xij=0.另外,引入辅助变量yijt表示第i个服务模块的第j个模块组件在时间块t的任务结束状态,即如果时间块t是该模块组件结束时间,则yijt=1;否则yijt=0.

优化问题的目标有如下三个:

1)最小化总服务成本CAll;2)最小化总服务处理时间TAll;3)最大化顾客需求指数I.

模型的基本假设如下:

1)总服务成本由固定成本和变动成本构成,其中变动成本和服务单位成本是线性加总关系.该假设被多项相关研究所采用[42-44].

2)顾客需求和服务产品属性之间的复杂关系可用QFD中的质量屋进行近似表达,即采用定量定性结合的方式通过质量屋来表示二者的映射关系.该假设被文献[4, 45-48]等所采用,涉及多个服务产品和有形产品的案例.

3)顾客对服务的顾客需求指数由服务模块的重要度评估分值线性加总获得.该假设被文献所采用[4],且在一些针对有形产品的研究中也有类似的假设[49].

为统一建模方便,在可选模块中增加一个“虚模块组件”,其对应的服务处理时间、服务单位成本和顾客需求指数均为0,这样服务模块可统一按照必选模块进行建模.另外,为方便服务流程时序关系的表达,模型中增加了一个“虚模块”,其中包含一个“虚模块组件”,并将流程的结束节点设置为虚模块的前序节点,这样可以用sNm+1来表示整个服务流程的结束时间.

3.2 数学模型

考虑服务流程时序关系和时变资源约束的服务配置多目标优化模型(P)表示如下

(1)

Obj2: MinTAll=sNm+1

(2)

Obj3: MaxI=

(3)

s.t.

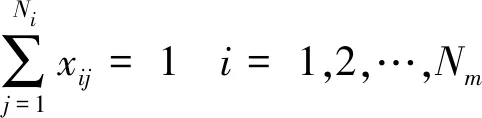
(4)

i,i′=1,2,…,Nm+1;i≠i′

(5)

xij≥δiji′j′xi′j′i,i′=1,2,…,Nm;

j,j′=1,2,…,Ni;i&j≠i′&j′

(6)

(7)

l=1,2,…,L;t=1,2,…,T

(8)

j=1,2,…,Ni

(9)

j=1,2,…,Ni

(10)

CAll≤CR

(11)

TAll≤TR

(12)

s1=0,si≥0i=2,…,Nm+1

(13)

xij=0 or 1i=1,2,…,Nm;j=1,2,…,Ni

电能替代技术主要包括三个方面：(1)发电侧。主要强调电力源头的清洁化和绿色化，从源头上降低对化石能源的依赖，从而加快对环境的保护及改善作用；(2)电网侧。主要强调电能从远方的远距离、清洁传输。由于我国能源资源的分配不均，造成的我国西南、西北地区的太阳能、风能等可再生清洁能源通过交直流特高压输送到东南沿海一带，降低传统能源的新增以及继续大量使用；(3)用户侧。主要强调终端能源消费中优先利用电能。首先是将工业锅炉、供暖锅炉等改为用电取热利用，减少煤炭的直燃利用；其次是将传统燃油汽车、港口岸电等以石油提供动力或者生活用能的项目改成用电；最后是为了改善作业环境，利用厨房电气化等项目的电能替代实施。

(14)

其中M是一个比较大的正数.Obj1表示顾客所选择服务配置的总费用.Obj2表示顾客所选择服务配置的总服务长,由虚模块的开始时间来进行等价表示.Obj3表示顾客所选择服务配置的顾客需求指数,由需求权重和两级QFD质量屋计算而来.约束(4)表示每个服务模块中的模块组件只能有一个被选中.约束(5)表示服务模块节点在服务流程中的时序关系.约束(6)表示服务模块组件之间的相容配置关系.约束(7)表示服务模块组件之间的排斥配置关系.约束(8)表示在整个服务过程中各模块组件所占用的资源不能超过其上限.约束(9)和约束(10)限定了辅助变量yijt的取值符合其定义.约束(11)和约束(12)分别表示服务的总费用和总工期不能超过顾客给定的上限.约束(13)表示服务组件开始时间的初始设定和非负约束.约束(14)给出了配置决策变量的具体定义.

模型(P)主要用于含有服务流程和时变资源约束的复杂服务,但也可适用于更一般的情形.如果服务产品没有服务流程,可将邻接矩阵元素φii′全部设为0,使得模型中的约束(5)失去作用;如果服务过程没有时变资源约束,可以删除约束(8)或将Rlt设为一个大的正数.

4 求解算法

上述模型的三个目标函数均为线性,但约束中存在非线性约束,因此是一个非线性整数规划模型.对于多目标优化模型,比较简单的方法是几个目标加权求和转变成单目标,但权重往往主观而不易设定,即使采用TOPSIS等方法也有类似的问题.本研究采用直接求解Pareto解集并进行聚类和交互选择的方法.对于中小规模问题,采用精确算法获得问题的Pareto前沿解集;对于大规模问题,采用智能启发式算法获得问题的非支配解前沿.

4.1 精确求解算法

通过分析多目标优化模型(P)可知,只有一个非线性的约束,即约束(8).但是该约束中的决策变量均为0-1变量,容易将其转换成等价的线性约束.定义一个新的辅助决策变量zijt(i=1,2,…,Nm;j=1,2,…,Ni;t=1,2,…,T),将模型中的约束(8)替换为以下约束

l=1,2,…,L;t=1,2,…,T

(15)

M(2-xij-yijt)≥1-zijti=1,2,…,Nm;

j=1,2,…,Ni;t=1,2,…,T

(16)

zijt≤xij,zijt≤yijti=1,2,…,Nm;

j=1,2,…,Ni;t=1,2,…,T

(17)

zijt=0 or 1i=1,2,…,Nm;

j=1,2,…,Ni;t=1,2,…,T

(18)

转换后多目标线性优化模型的决策变量是0-1量,系数可以规范化为整数类型的参数,可以采用精确算法求得Pareto前沿解集.本研究采用Lokman等[50]提出的目标函数值空间划分算法,其特点是代码实现容易且调用单目标线性整数规划的求解过程比较简单.该方法的思路是将多目标优化问题转换成单目标优化问题,每一次求解单目标线性整数规划问题得到新的非支配解,然后利用新的非支配解划分搜索空间,剔除被该非支配解所支配的空间,并更新非支配解集,重复以上过程直到没有新的非支配解生成,得到多目标优化问题的全部Pareto解集.求解每个子问题的单目标线性整数规划模型时,可以采用CPLEX等优化软件进行计算.

MaxI-ε(CAll+TAll)

(19)

s.t.

约束(4)～约束(14)

CAll≤b1

(20)

TAll≤b2

(21)

其中ε为一个非常小的正数,目的是将多目标问题转换成单目标问题,并避免产生多目标问题的弱有效解.向量b=(b1,b2)表示Obj1和Obj2的目标函数上界.

步骤1初始化b0,0=(M,M),调用线性整数规划模块(如CPLEX)求解单目标问题(Pb0,0),如果无解则转步骤4;否则令n=1,z1=z(Pb0,0);

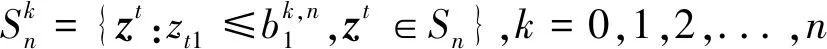
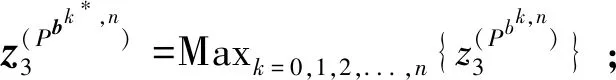
步骤4输出Sn,程序结束.Sn中包括了问题(P)的所有非支配解.

4.2 NSGA-II算法

对于大规模问题,问题解空间存在组合爆炸问题,精确求解算法无法在用户需要的时间内获得结果.因此,设计亚启发式算法来求解大规模情形下的服务配置问题.NSGA-II算法[51]是在NSGA的基础上改进的亚启发式算法,在许多复杂优化问题中都有成功的应用.本研究中求解服务配置模型的染色体主要采用整数编码结构,模型约束用罚函数法处理,遗传操作采用单点交叉和邻域变异.算法主要步骤描述如下.

步骤1初始化变量和参数,如模块组件编号Iij、时间tij、成本cij、重要性指数pij、邻接矩阵φii′、种群规模N、遗传代数G、交叉算子px和变异算子pm;

步骤2根据给定的种群规模数N,初始化种群pop;

步骤3通过二元竞标赛方式选择子代个体,并进行交叉和变异操作产生子代种群popChildi,其中i=1,2,...,G;

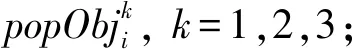
步骤5进行带精英保留策略的非支配排序:

步骤6重复步骤3,依次类推至迭代次数到设定的G,算法结束.获得Pareto前沿解集.

5 案例分析和数值实验

5.1 案例分析

下面以某装修公司为例,对本研究提出的服务配置方法进行详细说明.

步骤1建立装修服务的模块化结构.对装修服务进行特征分析,利用服务模块化设计思想,将装修服务流程划分成16个服务模块以及对应的46个模块组件配置,具体名称及其基本属性值(如时间、费用、性能等)如表1所示.表2为装修模块之间的紧前后序关系,其中“1”为横向模块是纵向模块的紧前序关系,“0”为无紧前后序关系.每个装修服务模块组件需要占用不同的人工资源,本案例主要考虑整个装修过程中的电工资源,结合公司实际情况对模块4和模块15中的组件I41、I42和I152分别设定2个、 2个和3个人工资源.

表1 装修服务模块及其模块组件信息

表2 服务模块间关系的邻接矩阵

为便于建模,在可选模块中添加一个“不选择”模块组件,则可选模块成为必选.在模块组件中,I42和I142,I13和I142,I62和I103,I94和I113,I11和I153,I13和I73,I11和I132存在相容关系;I93和I112,I11和I83,I11和I162存在相斥关系.

步骤2构造装修服务两级QFD质量屋.装修公司专业技术人员对装修模块需求和工程特性进行调研,通过借鉴QFD产品质量设计四级质量屋结构中的前两级(即产品规划和零部件规划)[45-48],先后构建服务规划质量屋和模块配置质量屋,将顾客需求重要性映射到服务组件,如图2所示.

图2 顾客需求的两级质量屋映射图

通过装修公司调研和分析,装修中有6个顾客主要需求:CR1-安全性、CR2-专业性、CR3-环保性、CR4-经济性、CR5-实用性、CR6-舒适性;13个装修服务主要属性:SA1-方案设计的多样性、SA2-施工过程的专业性、SA3-水电改造的安全性、SA4-防水工艺的可靠性、SA5-施工材质的环保性能、SA6-房屋吊顶的美观性、SA7-厨卫环境的整洁性、SA8-瓷砖铺贴的质量、SA9-木工制品的耐用性、SA10-油漆的质量、SA11-喷刷工艺的质量、SA12-工程的外观质量、SA13-整体保洁的质量.通过工程人员分析,该13个装修服务主要属性有高内聚性,因此不考虑自相关关系.

步骤3建立装修服务配置问题的多目标优化模型.装修配置优化过程就是在满足一定条件约束下(如本案例中服务组件之间的相容与相斥关系、顾客要求装修总时间TAll≤70 d、装修总费用CAll≤16万元),找出服务配置方案中使顾客获得最小装修费用Cmin、最短装修时间Tmin和最大顾客需求指数Imax.模型中,Obj1根据表1中的成本列进行构造,Obj2根据表1中的时间列和表2的邻接矩阵进行构造,Obj3根据步骤2的质量屋参数进行构造并按照模型目标函数进行计算,其中Obj2受约束(5)和约束(8)影响,后者是对电工在不同时期的时变资源约束.本研究考虑不同服务组件在服务模块的最早开始时间和最晚完成时间之间的时变资源约束,计算企业能够提供资源数高于服务组件所需资源数的天数之和,若该值大于服务模块组件所需执行的时间,则不影响整个装修工期.表3为项目开始后12周(84 d)中可用电工人数.

表3 装修服务的时变可用电工人数

步骤4多目标优化模型的求解.本案例共计13 436 928个配置组合方案,属中小规模问题,通过全枚举算法求解多目标模型,分别运行1 180 s和803 s可得本案例精确Pareto前沿解集,包含解个数Pn=334,解分布情况如图3中的(b)所示.本研究所有算法均采用Matlab2016编程,计算机配置为CPU2.7GHz和内存8GB,操作系统为Windows 10.

(a) 初始解

(b) 精确Pareto前沿解集

采用4.2节NSGA-II算法求解本案例,在交叉概率0.9、变异概率0.1、种群规模300、迭代次数1 000时,运行时长107 s(3次运算均值).算法每次运行均可得到与精确算法相同的Pareto解集,程序运算的初始种群和算法迭代之后最终获得的Pareto前沿解集分别如图3 中的(a)和图3中的(b)所示.

算法在不同种群规模下得到快速有效收敛,如图4所示.在200/300/400种群规模下,分别通过507/240/176次迭代即可收敛到Pareto前沿解集,说明算法有良好的收敛性能.

(a) 种群规模=200

(b) 种群规模=300

(c)种群规模=400

为观测不同遗传算子可能对Pareto解集产生影响,对遗传迭代过程中交叉概率算子和变异算子进行组合实验.利用指标间距度量Spacing(个体空间分布情况)值[52]评价算法性能,通过组合实验(3次平均)计算结果和运行时间发现当交叉概率=0.9和变异概率=0.1时效果最好,即间距度量Spacing与精确解Spacing=3.86差值为0且执行时间最快,具体的实验结果如图5中的(a)和图5中的(b)所示.

(a)组合实验解与精确解的Spacing差值图

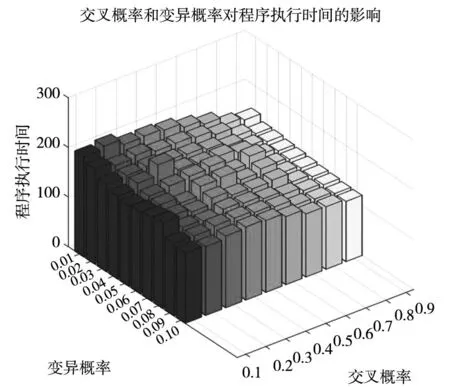
(b) 不同概率组合的程序执行时间

步骤5解集的缩减和交互选择.已求得的Pareto解集Pn=334,解个数太多不利于用户交互选择,故采用K-means聚类将Pareto解集聚为5类,计算聚类中心点,“·”为聚类的中心点,如图6中的(a)和图6中的(b)所示,图6中的(b)为图6中的 (a)旋转图,聚类效果可视效果更好.

(a)原始角度

(b) 旋转角度

然后,再利用目标优化解集的欧氏距离计算得到离5个聚类中心最近的配置解,得到缩减解集如表4所示.其中,表4前5行以第三个目标值(客户需求指数)作为第一排序准则进行降序排序,后3行则分别按照单个目标进行计算后所给出的服务配置方案.

表4 K-means聚类后的装修服务配置组合示例

从上述结果可知,问题最优服务配置组合Pareto解集共有334个前沿解,聚类可得五种不同装修方案.装修服务公司向顾客提供方案集合,顾客可对这些解的目标进行调整和交互选择,选择最满意的装修服务配置组合.

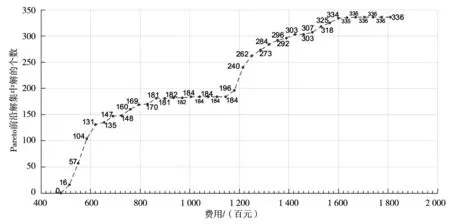
图7 装修总预算对Pareto解集中解个数的影响

1) 当减少装修总预算,Pn逐渐变少,反之则逐渐增多.因为总预算的增加和减少会对符合约束的可行解产生影响,则产生的Pn也随之变化;

2) 当CAll≥16.7万元,Pn保持不变,Pn=336.说明当CAll=16.7万元时,所得到的Pareto解集中的解能够支配所有可行解,再增加装修预算将不再影响推荐装修方案结果;

3) 当CAll的范围在[1 180,1 215]百元时,Pn从196增至240,增幅变化较大,其被支配的可行解变化较多,可行解在此区间的密集性比较高,此区域为装修总预算的敏感点;当CAll的范围在[1 005,1 145]百元时,Pn值始终稳定在184,此区域内装修预算不影响推荐装修方案结果.

为了进一步说明本研究中考虑时序约束和时变服务资源的必要性,分别将本案例的模块间时序约束和时变人工资源约束去除,得到对应的Pn、目标值变化情况、解集中的解针对原问题的可行性等情况,对比结果可知:1) 当不考虑时序约束时,装修工期目标函数平均值明显高于原问题,说明增加时序约束关系可以使更多服务模块并发执行,因此缩短了装修工期;没有时序约束所得Pareto解集中的解针对原问题全部不可行,且大部分被原问题解所支配; 2) 当不考虑时变资源约束时,服务提供商能够在任何时段供应足够人工资源以保证项目的实施,从Pareto解集来看其方案更优,但本例只考虑了电工资源,对原问题影响有限.

进一步分析电工人数对最优解目标值的影响.保持其他时段不变,分别对某一特定时段(周次)内的可用电工人数以1个单位持续增加或减少,所得Pareto解集不再变化时则停止改变服务资源量,记录结果如表5.“--”表示增加或减少电工人数均对解集不产生影响.

表5 调整电工人数对原问题解集的影响

针对表5中电工人数变化,对解集中解个数、目标值变化情况、解集中解针对原问题的可行性等进行分析,如表6所示.

表6 电工人数调整后Pareto解集的变化情况

结合表6可以得出以下结论和管理建议:

1)当项目工期在第2周时,减少1个电工资源将导致没有可行解;但增加电工资源则不影响最终解集的Pareto前沿分布,说明第二周增加电工人数意义不大.

2)当项目工期在第3周时,减少1个电工资源将会缩减Pareto解集个数.通过对Pareto解集数据进行分析,对比原问题的解集数据可知电工数量的减少只影响了Pareto解集中的少部分区域.因此,如果在此时段资源比较紧张时,可酌情抽调该资源前往其它时段或其它项目.

3)当服务项目工期在第8周或第9周时,增加2个电工资源后,Pareto解集中解的个数有显著增加.如果人工充足,服务供应商可考虑在此时段增加2个电工资源,以提供更加丰富和优质的服务组合方案.

4)当服务工期在第1周和第10周时,服务资源的增减对配置结果不产生影响,可将过剩资源调配到其它时段或其它项目.

5.2 数值实验

为进一步评估所设计的NSGA-II算法在求解服务配置问题上的效率,随机生成带有时序关系和资源约束的服务配置仿真案例,进一步验证精确算法和亚启发式算法的运行效率.

对于NSGA-II算法的性能评价,主要从解集的收敛性、均匀性和广泛性等三个维度做算法评估分析[52-54],分为两种情况:1) 已知精确Pareto解集:主要采用间距度量(Spacing)、当代距离(generational distance,GD)、覆盖率(coverage)、错误率(error ratio,ER)等指标;2) 未知准确Pareto解集:主要采用GD、倒代距离(inverted generational distance,IGD)、超体积(hyper volume,HV)、超体积差(hyper volume difference,HVD)等指标.随机生成不同规模案例基础,设置种群规模300,迭代次数1 000,对第一种情况采用小规模案例(模块数=20)进行实验,结果如表7所示;对第二种情况采用大规模案例(模块数=50)进行实验,结果如表8所示.

表7 精确Pareto解集已知时的数值实验结果

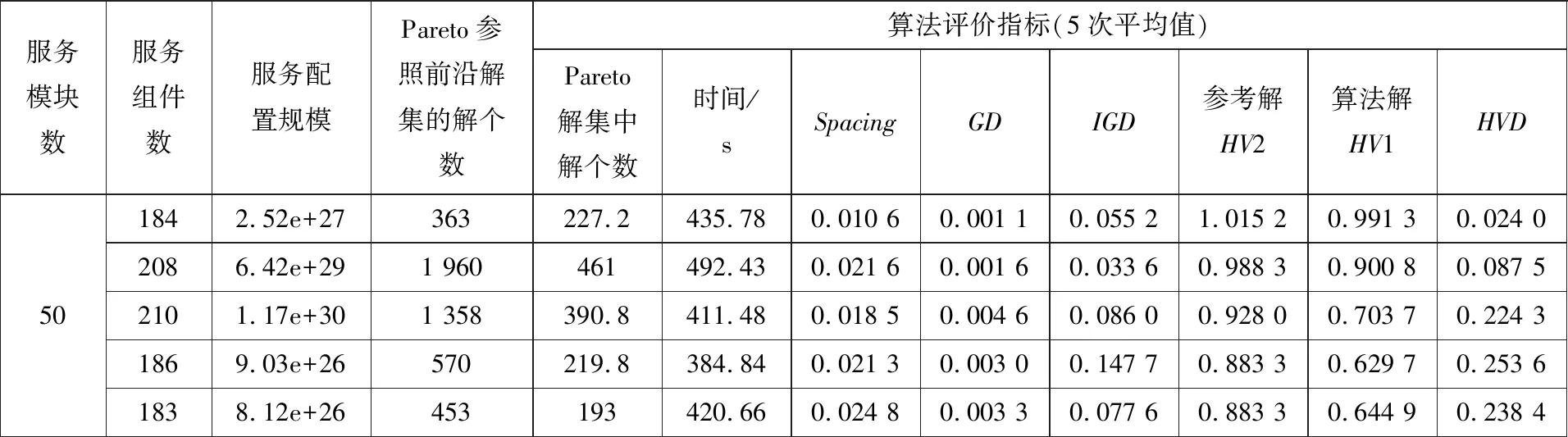
表8 精确Pareto解集未知时的数值实验结果

表7中,GD表示NSGA-II所得解到精确解之间的平均最小距离,GD值越小表明越接近于精确解,当GD=0时,即算法所得解均包含在精确解集中;Coverage表示NSGA-II所得解与精确解之间支配关系个数与算法所得解个数的比值,即解的覆盖率,Coverage值越大说明所得解越倾向于精确解,当Coverage=1时,即精确解完全覆盖算法所得解;ER表示算法解中不属于精确解集的比例,当ER=0时,即算法得到的解完全属于精确解集.结合以上三个指标,再根据NSGA-II算法和精确解算法所得解个数及Spacing值,表中指标数据充分说明算法能够快速得到较为理想的解集,具备良好的收敛性,能够很好的为服务提供满意的解决方案.

表8中,IGD表示参照前沿解到NSGA-II所得解之间的平均最小距离.Pareto参照前沿为通过本算法更大种群规模(2千)和更高迭代次数(2万)所得的参照Pareto解集,具备更趋于Pareto精确解集的趋势.因此,由GD和IGD的数据可知,算法所得的解比较倾向有参照解,只有很少一部分会被参照解所支配,说明算法能够较快收敛到较为理想的结果集.HV指标表示Pareto前沿解集与某一参照点所围成的目标空间体积,HVD指标为同一参照点与参考Pareto前沿解集和算法Pareto前沿解集之间的HV差值,可评价算法的收敛性.从表中数据可知HVD值比较小,说明算法解集已经靠近参照Pareto前沿解集,故算法具有较好的收敛性.

6 结束语

服务配置可在模块化服务的基础上针对特定的需求为顾客提供最适合的服务,是实现服务大规模定制的重要途径之一.在服务配置的过程中如果忽略服务流程的特征,可能会导致配置生成的服务无法充分利用企业资源和满足顾客需求.本研究的研究工作总结如下:1)在服务配置中考虑了服务流程的时序关系和时变资源约束,建立了服务配置问题的多目标优化模型,并将模型转化成了等价的线性形式; 2)针对小规模问题设计了空间划分精确算法以获得模型的Pareto前沿解集,针对中大规模问题设计了NSGA-II算法以获得模型的非支配解前沿.数值实验的结果表明两种算法均具有较好的效率; 3)通过一个装修服务实例的配置结果分析,比较了考虑和不考虑服务流程特征的几种情形,说明了服务配置中考虑时序关系和时变资源约束的必要性,并针对案例进行了敏感性分析,主要管理启示包括:1)服务预算或最大服务工期的变化只在一些特定范围内才对服务配置方案有显著影响;2)服务提供商可考虑对一些关键服务资源进行调配,进一步提升最优配置方案中的顾客满意度.本研究提出的服务配置优化模型和算法可形成软件模块嵌入服务型企业的管理信息系统中,帮助企业为不同类型的顾客快速生成个性化服务方案,达到改善顾客满意度、节省服务过程费用、提升市场占有份额等目的.

本研究在数学模型的基础上,可以进一步进行相关扩展.例如,公司可能对服务模块设定执行时间窗,要求某些服务模块组件在一定的时间窗内执行,这可以很容易在原模型的基础上通过增加时间窗约束来进行扩展.另外,最大服务周期的设定可以通过时序网络图的计算来估算其最晚结束时间,从而可以改善求解算法的效率.这些模型扩展可以根据企业需要进行,并不影响数学模型表示的复杂程度,且模型仍然可以是线性形式.

本研究的局限之一是所提的方法主要适用于基于服务模块化的服务.服务的范畴非常广泛,有的服务很难进行模块化.因此,将来的研究可从以下几个方面继续深入: 1)顾客需求的不确定性方面.由于顾客需求的不明确和定性表达等,导致服务配置模型的表示和求解更加复杂; 2)多顾客同步或异步模式方面.由于多个不同类型的顾客同时在线参与配置,配置问题的复杂度将显著增加; 3)优化求解算法方面.多目标优化算法的求解效率需要不断改进,根据问题的特性寻求更高质量的求解算法.