我国银行体系系统性风险测度与评估①

马家丽, 庞小川, 朱书尚*, 莫莹军

(1. 贵州财经大学大数据统计学院, 贵阳 550025; 2. 中山大学管理学院, 广州 510275;3. 中山大学数学学院, 广州 510275)

0 引 言

近十多年来美国次贷危机、欧债危机的爆发极大引发了人们对金融体系系统性风险的关注.金融体系作为资金融通的渠道,其稳定性关乎实体经济乃至整个国民经济的健康发展.金融体系系统性风险不是个别金融机构破产或个别金融资产价格大幅下跌的风险,而是由某个/类特殊事件引发的多家金融机构破产或金融市场崩溃,从而导致金融体系功能无法正常发挥的风险[1, 2].如何防范金融体系系统性风险、维护金融稳定已成为金融监管当局及学界重点关切的问题.当前,中国经济形势复杂,一方面面临国际贸易摩擦;另一方面国内经济形势严峻:房价过高、杠杆率偏高、经济增长乏力等.这些风险因素都有可能成为系统性风险爆发的导火索. 2017年我国进入银行业强监管的时代,为守住系统性风险不发生的底线,银监会掀起了一场监管风暴.严监管下,我国银行体系总体运行平稳,但仍然出现了诸多问题:锦州银行2018年和2019年上半年皆出现重大亏损以至于无法提供财务报告;包商银行由于出现严重的信用风险而被接管;多家银行由于授信及监管不当而受到处罚;债券市场也陆续出现违约.由此可见,我国金融体系风险监测与管理工作仍有待进一步科学规范与加强.因此,深入研究我国银行体系系统性风险,识别出系统性关键行业及资产,对防范和化解我国金融体系系统性风险具有重要的理论意义和实践价值.金融体系主要由金融机构体系、金融市场和监管部门等构成.本文主要研究金融机构体系系统性风险.为简洁起见,在不至于引起歧义的情况下,本研究亦以“金融体系”狭义代指金融机构体系.

金融体系由于自身业务的网络关联性,经济中的一个小幅波动亦可能促发金融体系系统性风险.如图1所示:一方面,金融机构常面临相同的外部资金需求者和投资项目,例如,各银行贷款集中于某一行业或购买同一种债券,因此金融机构的外部资产持有必然存在重叠.另一方面,金融体系为保证流动性需求,体系内部机构间往往存在相互拆借行为,这种相互借贷将整个体系联系起来构成了借贷网络.由此,当外部资金需求者违约或银行持有资产贬值时,金融机构可能会面临财务危机而出现破产(称为初始破产,相应的破产机构称为初始破产机构).初始破产机构会通过出售其持有的外部投资资产来偿还债务,这一行为使得大量资产涌入市场会造成资产价格下跌,从而导致持有相同资产的其它金融机构的资产贬值(称为外部资产重叠价格传染),并可能进一步引发新的机构破产.破产机构不能足额偿还相关机构的债务,经由相互借贷网络使得相关机构内部借贷资产损失(称为内部借贷违约传染),亦可进一步引发新的机构破产.如此循环往复,外部资产重叠价格传染和内部借贷违约传染共同作用可将风险的影响范围扩大,使得金融体系的损失不断加重,进而引发系统性风险.有鉴于此,金融体系系统性风险的度量必须综合考虑内部借贷及外部资产重叠的联合传染放大效应,否则金融体系系统性风险将被大为低估.

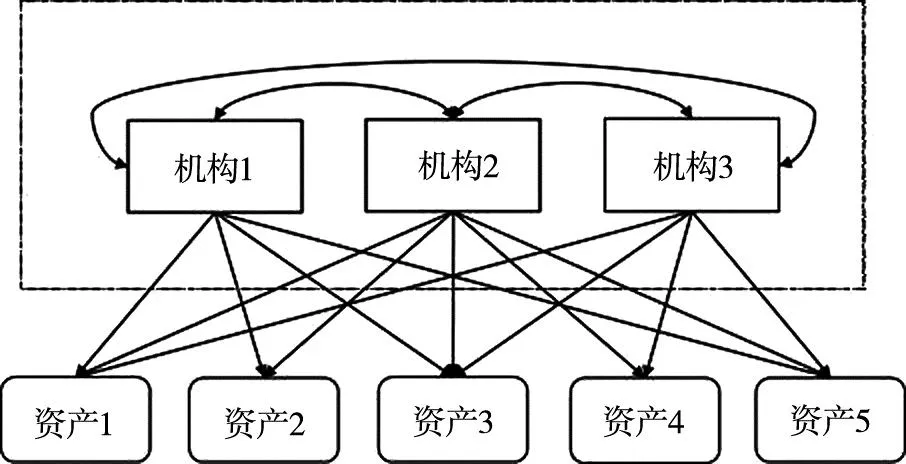
图1 金融体系内部相互借贷及外部资产重叠

国际上对于系统性风险的研究,主要分为两类:一类从金融机构市场数据出发,通过CoVaR[3-5]等风险指标分析金融机构尾部风险事件对金融体系整体风险的影响;另一类则从金融机构资产负债结构出发,利用网络模型,考虑风险传染机制对系统性风险的影响.本研究属于后者.Allen 和 Gale[2]与Eisenberg 和 Noe[6]等率先利用网络模型分析金融机构内部相互借贷对金融体系系统性风险的影响.特别是,Eisenberg 和 Noe[6]给出了金融体系受到冲击后,金融机构的内部债务清算机制及均衡支付向量的计算方法(简称E-N模型),为系统性风险传染机理及测度的研究和实践打开了新的篇章.自E-N模型提出以后,基于网络模型对金融体系系统性风险的研究不断涌现.Cifuentes 等[7]在E-N模型的基础上考虑金融机构持有外部单一资产的情形,并讨论了资产折价变卖(流动性)对金融体系系统性风险的影响.Glasserman 和 Young[8]在E-N框架下分析了金融体系系统性风险传染可能性大小(概率)与金融机构内部相互借贷网络结构之间的关系.Amini 等[9]分析了E-N 模型加入持有外部单一资产后,金融机构均衡清算向量的存在性和唯一性问题.在相同的模型下,Chen 等[10]对风险传染的网络效应和流动性效应进行对比分析,指出资产流动性不足更可能引发系统性风险.Feinstein[11]将E-N模型拓展到持有外部多种资产的情形,探讨了清算向量的计算问题,并研究了当机构出现危机时资产的变卖策略.在相同的模型上,Ma 等[12]进一步从理论上分析了内部相互借贷及外部资产重叠对金融体系系统性风险的联合影响机制,指出二者有很强的共振效应,并据此给出了金融体系系统性风险的一种启发式最优救助策略.在利用E-N模型对金融体系系统性风险进行测度的实践方面,国际上,Elsinger 等[13]对奥地利银行体系系统性风险进行了评估,较早给出了银行体系系统性风险的分析框架.值得指出的是,虽然没有像E-N模型对机制的深入探讨,Caccioli 等[14]、 Caccioli 等[15]同样利用网络模型并结合模拟方法研究了资产重叠对金融体系系统性风险的影响.其分析结果表明机构间债务违约传染和外部资产重叠价格传染对系统性风险的联合影响非常显著.

类似地,对于我国金融体系系统性风险的研究也分为两类:一类基于市场数据,分析金融机构或者行业与系统性风险之间的关系.梁琪等[16]、陈守东和王妍[17]以及陈湘鹏等[18]等文献基于金融机构收益率数据,通过MES、SES、CoVaR及SRISK等风险指标测度金融机构对金融体系系统性风险的影响.李政等[19]和杨子晖等[20]将计量模型与有向无环图结合分析金融机构或行业尾部风险传导的网络效应.裴茜和朱书尚[21, 22]研究了我国股票市场暴跌暴涨时期在行业层面上风险传染的现象、渠道及网络特征.宫晓莉等[23]利用方差分解网络构建金融机构间信息溢出网络,分析表明高通胀和高杠杆均可加剧系统性风险.基于银行系统性风险相关面板数据,赵静和郭晔[24]的分析表明存款保险制度实施初期会扩大影子银行业务从而推升系统性风险.另一类基于金融机构资产负债数据,从相互借贷或者资产重叠的角度分析相互借贷及资产重叠对系统性风险的传染、放大效应.基于E-N模型,黄聪和贾彦东[25]利用我国银行体系之间的支付数据,考虑银行间内部风险传染机制,分析我国银行体系系统性风险与银行间支付网络之间的关系.隋聪等[26]、隋聪等[27]通过网络模型,模拟研究相互借贷网络的传染效应.李世泽等[28]考虑银行间相互借贷的情况下,房地产业贷款对银行体系系统性风险的影响.通过给定风险传染阈值,方意[29]利用最大熵方法恢复金融机构间相互借贷数据,并据此模拟研究金融机构间借贷违约传染效应.范小云等[30]全面考虑了银行间的同业业务,通过核心—外围网络填补银行同业业务数据,并据此识别系统性重要银行.通过模拟分析,隋聪等[31]以及方意和黄丽灵[32]探究了资产重叠对系统性风险的影响.徐国祥等[33]通过贝叶斯分层图模型估计银行间的关联关系,结合银行间相互借贷数据,综合模拟研究了银行间的风险传染和放大效应.

如前所述,金融机构内部相互借贷所形成的金融网络,是导致系统性风险的关键因素之一.Elliott 等[34]和Acemoglu 等[35]的研究表明不同内部相互借贷网络对金融体系系统性风险传染的作用不同.然而,通常情况下,机构间相互借贷的详实信息无法获得,只能得到各机构内部相互借贷(资产/负债)的总额数据.因此,要分析金融体系系统性风险,一个必要的任务便是寻找合适的方法来恢复机构内部相互借贷数据.在以往研究中,Upper 和 Worms[36]提出的恢复机构内部相互借贷网络的最大熵法得到了较多应用[13],但该方法只能恢复出比较均匀的网络,与现实网络结构存在一定的差异.Boss 等[37]、Lubóy[38]、Cajueiro 等[39]及Raddant[40]等研究表明金融体系内部相互借贷网络具有小世界特性,且节点度服从幂律分布.Gandy 和 Veraart[41]提出的贝叶斯方法可以生成满足幂律分布的内部相互借贷网络,比最大熵法生成的网络更加接近现实.加之,该方法可生成一簇网络样本,相较于最大熵法只能恢复出唯一样本,在系统性风险评估中更加稳健.

综上所述,直接从市场数据出发利用计量方法测度金融体系系统性风险的研究,具有简洁直观的优点,但缺乏对系统性风险形成机制的探究.而利用网络模型,从金融机构资产负债结构所表达的相互关联关系出发对系统性风险的研究,更加强调风险形成的微观机制,但是真实金融网络数据难以完全获得,给实际应用造成了障碍.真实的金融体系系统性风险的准确测度,有赖于对风险来源、风险传染和放大机制以及真实数据的填补与恢复进行全面科学地整合.

商业银行体系(简称银行体系)作为我国融资主体,是我国金融体系中最核心的组成部分.中国人民银行披露的相关数据显示,2019年社会融资增量中80%左右为间接融资(1)数据来源于中国人民银行网站《社会融资规模当月增量时序表》,http://www.pbc.gov.cn/diaochatongjisi/116219/116225/3960224/index.html..银行体系的崩溃将导致整个社会资金融通功能的丧失,危及整个国民经济的运行.因此,银行体系系统性风险的监测和管理是我国金融体系风险管理工作的重中之重.鉴于此,并考虑数据的重要性及可获得性,本研究立足于我国实际情况,从现有银行资产负债结构真实数据出发,利用网络模型综合考虑银行内部相互借贷及外部资产重叠对银行体系系统性风险的影响.结合实际数据进行情景分析与压力测试,探究各风险来源对银行体系系统性风险的影响,由此识别我国系统性风险关键性行业和资产.利用宏观驱动因素将信贷端的违约与投资端的资产价格变动联系起来,分析相关宏观因素对系统性风险的影响.

相较于以往的研究,本研究的创新之处在于:第一,从我国银行体系特点出发,构建了基于风险“来源—传染—放大”机制的系统性风险测度模型.一方面,抓住了我国银行体系风险来源的主要方面,利用相关风险测度方法分析风险来源对银行造成的初始损失.另一方面,利用网络模型考虑相互借贷引发的违约传染及资产重叠引发的价格传染以及二者的叠加放大效应.由此对我国银行体系系统性风险传染机制及效应进行全面系统评估.第二,给出了“宏观—中观—微观”一体化系统性风险分析框架.将各银行资产负债数据及其持有的各类金融资产(相关债券指数)数据(微观)、各行业贷款违约率数据(中观)及我国宏观经济发展水平(GDP)和债务水平(各部门杠杆率)等数据结合,通过贷款违约因素和债券定价因素分析,把行业贷款违约率、债券价格变动与宏观因素有机联系起来,并由此综合分析相关宏观因素变动对我国银行体系系统性风险的影响,为宏观政策制提供有益借鉴.

1 我国银行体系系统性风险建模

我国银行的资产主要分为:贷款及垫款(简称贷款)、金融投资资产、银行体系内部拆借资产及现金等其它高流动性资产.根据实际情况,本研究建立了图2示意的我国银行体系系统性风险测度框架.如图所示,潜在的系统性风险形成过程如下:首先,银行体系受到冲击(风险来源)而发生初始破产.从我国银行财务报告可以看出,银行风险来源主要为贷款违约损失(信用风险)及金融投资资产价格下跌(市场风险和流动性风险);随后,内部相互借贷违约传染和资产重叠价格传染共同作用将风险影响范围逐步放大,从而可能引发银行体系系统性风险.

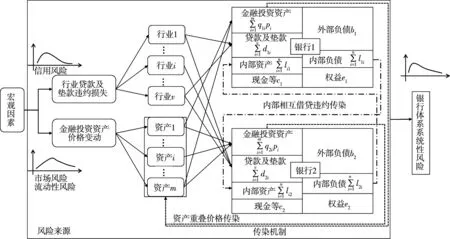
图2 我国银行体系系统性风险测度框架

在风险来源方面,对于贷款损失,考虑到数据的可获得性和风险测度的完备性,本研究将银行贷款按照行业进行细分考虑银行贷款违约损失.对于金融投资资产(主要为债券),由于无法获得银行债券持有的详细信息,本研究主要考虑债券的价格变动对银行总资产的影响.

为分析银行体系内部相互借贷引发的违约传染和资产重叠引发的价格传染对系统性风险的影响,本研究采用网络模型来刻画银行间的相互借贷及资产重叠情况:对于银行体系内部相互借贷,银行作为网络的节点,银行间债务往来作为二者之间的连边;资产重叠表现为二部图的形式,银行和金融投资资产作为节点,银行对资产的持有作为节点间的连边.依据上述网络(用矩阵表达)和扩展的E-N模型,设置合理的偿债原则及金融资产价格变动机制(清算准则),可以清楚地刻画风险的传染过程,并可由此分析不同风险传染机制的传染效应.在此基础上,结合情景分析与压力测试,对我国银行体系系统性风险进行全面地测度与评估.

为完成我国银行体系系统性风险全面的测度和评估,本研究需要具体地解决以下四个基本问题:1)银行体系发生初始破产后,由于银行间存在内部相互借贷联系,债权人如何分配破产银行的剩余资产?破产银行低价出售其资产将怎样影响其它银行的资产价值?经过风险传染,银行系统将达到怎样的新的均衡状态?为解决这些问题,需要对银行体系的清算过程进行建模; 2)通常情况下仅有各银行银行间资产及负债的总额数据可得,银行体系内部相互借贷的详细数据未知.在此情况下,为分析银行体系内部相互借贷网络的传染效应,必须要对银行内部相互借贷详细数据进行恢复; 3)银行体系风险来源作为系统性风险爆发的导火索,对其进行准确的测度是系统性风险分析的基础,也是识别系统性关键行业和资产的必要环节,由此必须对银行风险来源进行建模; 4)为分析不同风险传染渠道对系统性风险的放大效应以及评估我国银行体系系统性风险,度量不同风险来源对系统性风险的影响,识别系统性关键行业和资产,必须提出相关合理度量指标.接下来将对以上四个问题展开详细讨论,本质内容是对图2所示的物理模型及其背后的机制进行数学建模.

1.1 银行体系清算过程

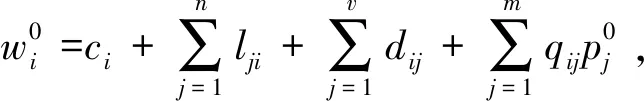
w0=c+LT1n+D1v+Qp0

其中1n、1v表示元素全为1且维度为对应下标n、v的列向量,其它符号具体含义如下

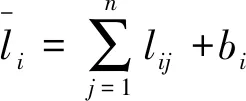
记银行由于贷款无法收回引发的初始损失为s=(s1,s2,…,sn)T.规定银行持有资产的初始价格p0=1.若初始冲击表现为价格下跌,则相应地将p0调整为下跌后的价格.银行遭受初始损失可能使银行出现流动性不足甚至破产.若如此,银行会发生资产甩卖行为,而此行为会进一步导致资产价格下跌.为刻画这一现象,引入如下设定.

假设1若银行不破产,则不改变其金融资产组合的结构及数量;

假设2金融资产价格变动在风险传染期间只受该资产抛售量的影响;

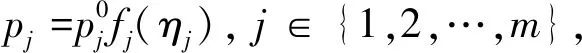
当银行体系中出现银行破产时(资不抵债),本研究依据Eisenberg 和 Noe[6]提出的如下三条“清算原则”对银行体系的价值进行清算重估:破产银行若存在剩余资产,则其必须将全部资产用于偿还债务(债务优先原则);若无剩余资产,则无需偿还债务(有限责任原则);债权人依照其额度大小按比例分配债务人的所有资产(按比例偿还原则).

设l=(l1,…,ln)T与p=(p1,…,pm)T为经历冲击后的实际支付向量和价格向量.此时,银行i的资产总额变为

(1)

根据清算准则,各银行的实际支付li应满足

金融资产j的价格取决于各银行的流动性不足情况及变卖策略.由于数据信息限制,本研究设定当银行破产时,将出售其所持有的全部金融资产.由此,在支付向量l及价格向量p下,银行i出售其持有资产j的数量占j资产总量的比例可表示为

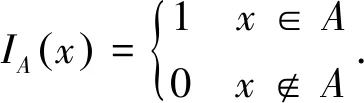
根据上述分析,经历风险传染后,银行体系实际均衡支付向量及价格向量应满足

其中(记x、y分别为n维列向量)

(x)+=(max{x1,0},…,max{xn,0})T

x∧y=(min{x1,y1},…,min{xn,yn})T

f(η)=(f1(η1),f2(η2),fm(ηm))T

显然,银行体系实际清算(均衡)向量l*和p*为等式(2)系统的不动点.据此,可以利用Ma[12]提出的如下迭代算法计算l*和p*(有限步精确得到或充分多步近似得到):

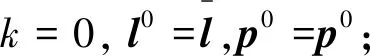
步骤2计算

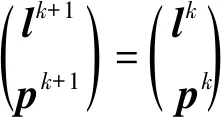
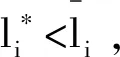
1.2 银行内部相互借贷网络的恢复

银行体系内部相互借贷网络作为系统性风险传导的重要渠道,准确地恢复内部相互借贷网络内部数据是度量系统性风险的关键工作之一.本研究利用Gandy 和 Veraart[41]提出的贝叶斯方法来生成节点度和权重服从幂律分布的内部相互借贷网络.由此,通过采样得到服从某一分布的一系列随机网络样本,构成系统性风险评估的基础.简要介绍借贷网络生成方法如下.

lij|{aij=1}～Exp(λij)

参数设定:为了生成符合实际特征的银行内部借贷网络(节点度和权重服从幂律分布),上述参数pij和lij按照以下方法设定.对任意i,j∈N,取

xi～Exp(1),

pij=g(xi+xj)I{i≠j}(i,j)

(ζ,ξ)～ψ(ζ,ξ)

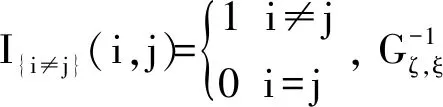
g(x)=β(γ/β)1-e-x(1-ln(γ/β)e-x)

若α=-1;否则

其中κ=(γ/β)α+1,0<β<γ≤1,α<0.当α>-2时,为保证0≤g(x)≤1,取

由此生成的随机网络其节点度和权重服从幂律分布的内部相互借贷网络.

后验网络生成:在上述给定的基准先验网络基础上,将银行体系实际内部相互借贷矩阵行和及列和数据作为新信息(可从资产负债表统计获得),利用马尔科夫链蒙特卡洛模拟(MCMC)方法[41](程序见R systemicrisk包)可得银行内部相互借贷的贝叶斯后验网络样本.

1.3 风险来源的建模

根据我国银行资产负债表将银行资产分为风险资产和无风险资产.无风险资产包括现金及存放中央银行款项.风险资产包括银行间资产、贷款、金融投资及其它.其中,银行间资产为境内存放同业银行款项加境内银行拆出资金;金融投资为以公允价值计量且其变动记入当期损益的金融投资、以公允价值计量且其变动计入其它综合收益的金融投资以及以摊余成本计量的金融投资;其它资产包括境外银行的拆出资金、存放境外银行款项、长期股权投资、固定资产、无形资产、商誉等.银行体系作为一个整体,风险来源有内部与外部之分.外部风险主要分为如下三类:1)外部借款人违约造成的贷款损失;2)金融投资资产价格下跌引发的金融投资资产损失,在我国主要由债券及类似债券的资产价格下跌引发;3)其它资产损失.内部风险为银行内部相互借贷资产损失,该损失仅当相关银行出现资不抵债才会引发,而银行出现资不抵债主要是由外部资产损失造成.由此,银行体系系统性风险的最终来源主要是外部资产的损失,内部相互借贷网络引发的资产损失应归结为风险传染放大渠道引发的损失.

如图3所示,贷款和金融投资资产分别占我国银行体系资产总额的49.63% 和27.69%,这两部分资产的风险是我国银行体系风险的主要来源.其它资产占10.26%,加之这类资产较为特殊:1)对于境外银行的拆出资金和存放境外银行的款项,由于数据缺乏,难以合理计量其风险,并且该部分资产数额较小; 2)长期股权投资是银行取得其它企业的股份.其主要对象为非上市公司,大部分采用成本法计价,且由于数据不足,目前无法对所有银行的子公司进行分析,因此无法度量其风险; 3)根据各商业银行的年度报告,固定资产主要包括房屋及建筑物、机械设备及其它固定资产等;无形资产包括软件和其它无形资产,这两类资产均采用历史成本法进行初始计量,在使用寿命内通过直线法等会计准则进行折旧和摊销,无法找到合适的指标对其风险进行度量; 4)商誉是银行收购项目协同效应的衡量指标,无法计量风险.综上原因,并考虑到在有限时间内这部分资产的价值变化较小,本研究在以下分析中将其等同于无风险资产,而主要分析贷款信用违约风险和金融投资资产的市场风险及流动性风险对我国银行体系系统性风险的影响.

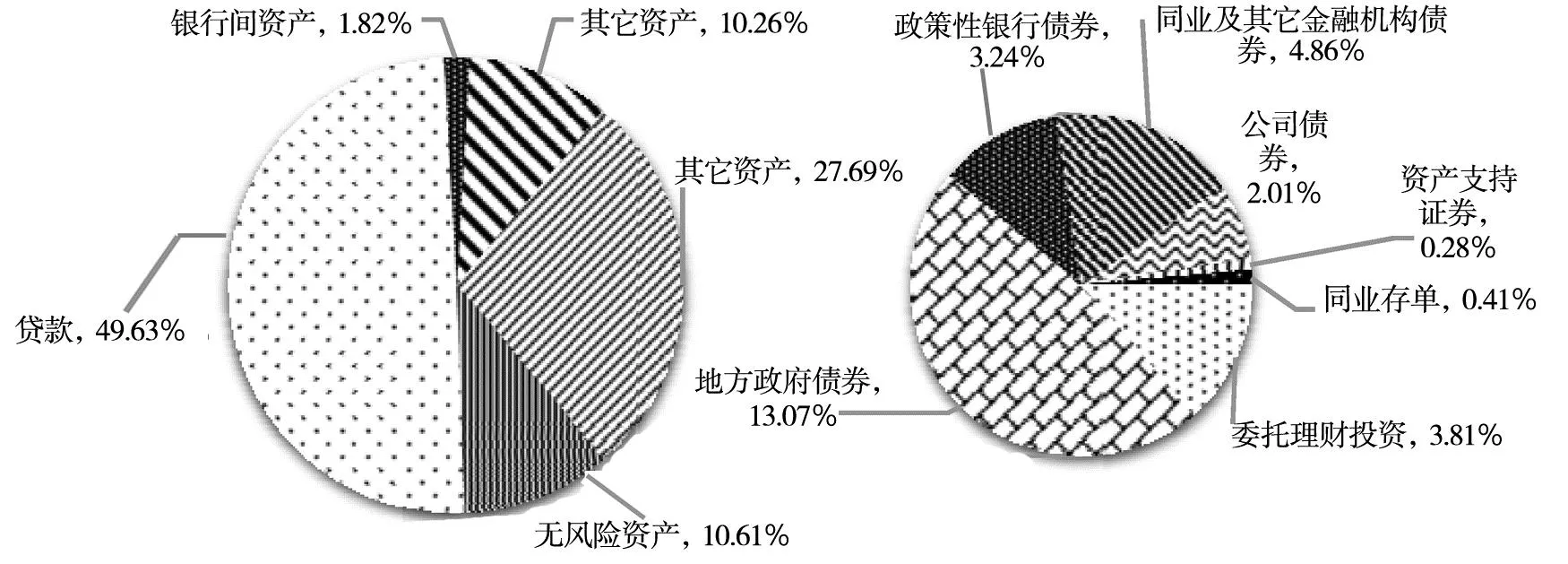
图3 银行体系各类资产占比

1.3.1 贷款的信用风险

贷款作为我国银行的主要资产,其信用风险对银行体系系统性风险的影响至关重要.对于单个银行来说,贷款的损失主要来源于借款人的违约损失.

由Credit Suisse First Boston提出CreditRisk+[43]模型是测度贷款组合信用风险最常用的模型.Bürgisser 等[44]进一步考虑了贷款者间的违约相关性,对原始CreditRisk+模型进行了改进.该评估模型有诸多优点:假设较少、只需输入很少的数据便可得到信贷损失分布、可以考虑行业间违约的相关性.本研究采用该改进模型对各银行贷款组合的信用风险源进行建模.给出各行业贷款违约率的均值、标准差及相关系数,利用CreditRisk+技术文档中的迭代算法可得各银行贷款组合信用风险损失的分布情形.

1.3.2 金融资产的市场风险

金融投资资产是除贷款外银行最主要的风险资产.通过财务报表附注信息,本研究将金融投资资产细分为:债券、资产支持证券、同业存单、委托理财投资(资管与信托、银行理财、基金投资、股权投资等,其中资管与信托、银行理财约占90%).其中债券按照其发行人不同分为:政府债、政策性银行债、同业及其它金融债及公司债.对于单个银行的各项金融资产组合而言,银行作为专业的投资者,其投资的资产组合是一充分分散化的组合. 由此本研究将银行每项资产近似于相应中债指数,利用指数价格变动刻画对应资产的价格变动,具体对应如表1所示.由于目前无法从已有的信息中判断委托理财投资的交易形式,且细分的委托理财投资无法一一找到合适的指数与之对应,由此本研究将其合为一类并选用信托指数衡量其价格波动.

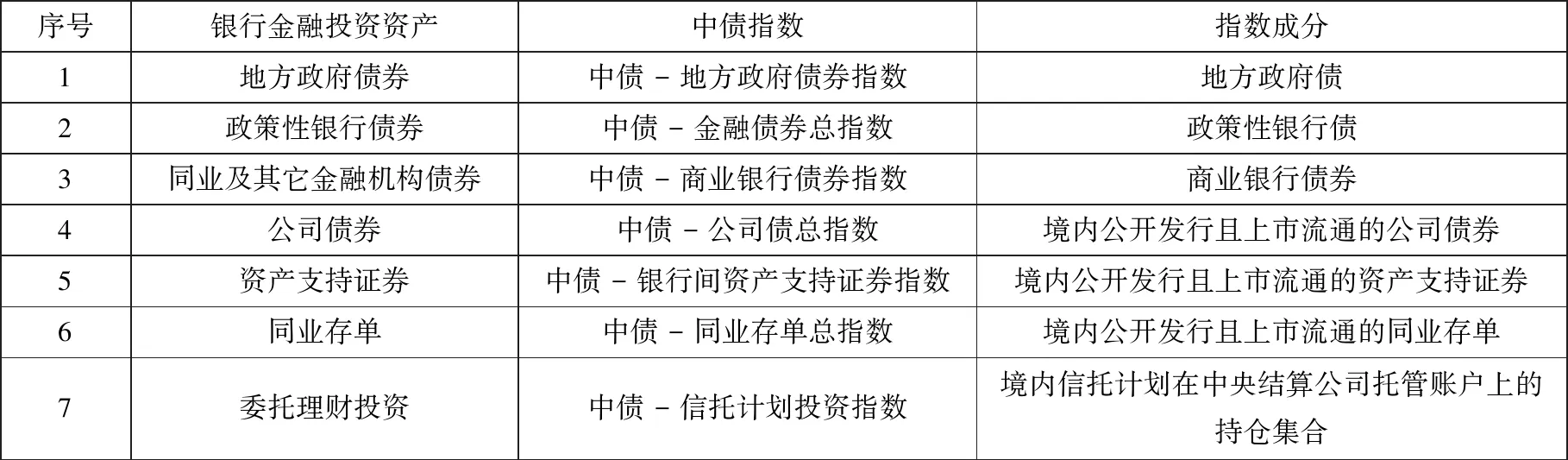
表1 风险投资资产与其对应中债指数

1.3.3 贷款违约与金融资产价格变动之间的相关性

银行体系系统性风险的度量,必须考虑银行所面临风险之间的相关性.根据上述分析可知,银行的贷款损失主要取决于各行业的贷款违约率,而金融资产的损失主要来自于资产价格变动.我国银行投资主要集中在债券上,因此只需要理清行业贷款(贷款组合)违约及债券价格之间的关系即可得到银行外部风险源之间的相互关系.基于此,本研究分别探究了贷款违约率和债券价格与宏观经济因素之间的关系,并对我国银行外部风险源之间的关联关系进行建模.

对于贷款违约率,Wilson[45]研究表明,贷款组合违约受到宏观因素的影响.由于贷款组合的违约概率在[0,1]上取值,该文通过Logistic模型建立贷款违约与宏观经济之间的关系. 基于此,研究建立如下Logistic模型

对各行业贷款违约率影响因素进行分析.其中,pit为行业i的贷款在t时的违约率,yit为宏观因素指数,通过如下回归模型

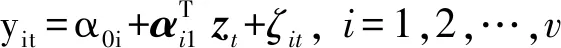
(3)

得到.其中zt为宏观经济因素向量,ζit为随机扰动项.

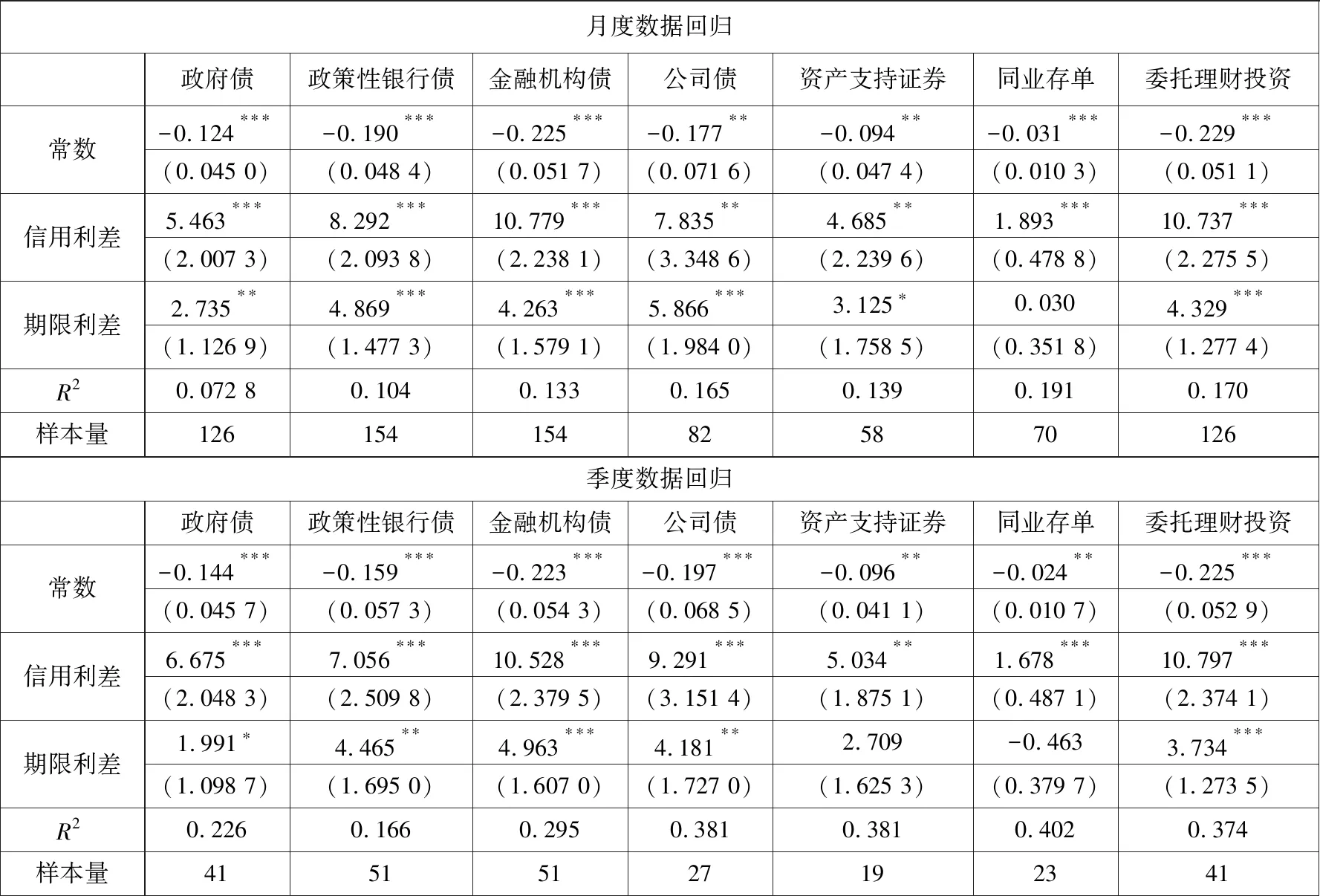
对于债券价格的变动,一方面,Fama 和 French[46]研究表明,市场当前的信用利差和期限利差对债券的未来超额收益率有较好解释能力.本文参照Fama 和 French[46]回归模型构建信用利差、期限利差和期望超额收益率的关系

rj(t,t+T)=β0j+β1jdpt+β2jtermt+

εj(t,t+T),j=1,…,m

(4)

其中rj(t,t+T)为时间跨度为T的预期超额收益率,dpt为信用利差,termt为期限利差,εj(t,t+T)为随机扰动项.另一方面,债券期限利差、信用利差亦受宏观经济因素影响.Davies[47]的实证结果表明宏观因素能显著解释信用利差.Fama 和 French[46]认为期限利差与经济周期相反,即在经济繁荣时较低,而经济萧条时较高.因此,为研究宏观因素对债券价格的影响(通过期限利差和信用利差),构建如下回归模型

(5)

其中εt和ϑt均为随机扰动项.

综合式(4)～式(5),给定宏观因子,可得各金融资产T期后预期价格[48]与当前价格之间的关系

pjt=E(pjt+T)e-(rj(t,t+T)+rt)T,j=1,…,m

(6)

当宏观环境变化时,信用利差dpt及期限利差termt将随之变动,期望收益相应变动,债券价格亦会发生相应变化.

综上,行业贷款违约率及债券价格都受到宏观经济因素的影响.一般情况下,当经济走低,企业发展滞缓,贷款违约率上升,与此同时人们进行金融投资所要求的风险溢价也上升从而导致金融资产价格下跌.反之,贷款违约率下降、金融资产价格上涨.通过宏观因素,可将贷款违约率变动与债券价格变动联系起来,为分析贷款违约损失与债券价格变动共同作用以及宏观因素对银行体系系统性风险的影响提供理论依据及方法准备.

1.4 系统性风险度量指标

根据前述分析,本研究具体的系统性风险测度方法如下:首先,随机生成10 000个银行内部借贷网络,并且随机地从“风险源”(比如贷款违约损失)抽取10 000个样本.然后,分别从这些网络样本和“风险源”样本中各随机抽取一个样本进行配对,通过计算清算向量,即可判定银行破产与否并可计算资产损失情况,如此重复10 000次,可得10 000个样本.最后,根据得到的10 000个样本计算出相应风险指标的统计特征.

为分析银行体系系统性风险的大小及风险传染机制对银行体系系统性风险的影响大小,识别出关键行业和资产,抓住系统性风险的主要且全面的特征,本研究引入如下四类风险度量指标.

银行稳定性测度:用各银行初始破产概率(频率)

反映银行的稳定性.该值越大,则银行越不稳定.

风险源关键性测度:用初始破产银行数量

风险传染效应测度:一方面,用初始破产的情况下传染发生(除初始破产银行外有新的银行破产)的概率

反映传染发生的可能性大小;另一方面,用被传染破产银行数量

整体风险(放大效应)测度:用银行体系资产总额损失额(单位:万亿元人民币)

反映银行体系系统整体的损失水平.特别地,对于银行体系资产总额损失wloss,本研究利用传统的风险值VaR进行风险度量.其定义如下

VaRα=inf{w∶P(wloss>w)≤1-α}

其中α表示置信水平.VaR本质上是分位数.后续分析中,分别用银行体系资产损失风险值VaR0.5(中位数)及VaR0.95(95%分位数)度量银行体系系统性风险损失的一般水平和极端情况.

VaR0.5

2 我国银行体系系统性风险测评

2.1 数据来源

关于银行资产负债结构数据主要来自于我国45家商业银行(具体银行名称及对应序号见附表1)2018年年度报告.Wind数据库显示,截止2018年末,我国商业银行总资产为203万亿元人民币,银行业总资产为261万亿元人民币,本研究考虑的45家商业银行资产总额为178万亿人民币,占商业银行总资产的88%,占银行业总资产的68%,可近似代表我国整个银行体系.各银行资产负债总额数据来自于报告中的资产负债表,各银行内部相互借贷总额来自于资产负债表附注信息.银行内部资产总额包括:存放境内同业资产及拆出境内同业银行的资产.银行内部负债总额包括:境内同业存放及拆入境内同业银行的资产.银行外部负债总额即总负债减掉银行内部(相互借贷)负债总额.银行外部金融投资资产按照资产负债表附注信息分类汇总得到.来自于Wind数据库的数据有:20个行业不良贷款率(2006年—2017年,按国民经济行业门类划分,包括19个门类,为将个人贷款纳入完整分析,本研究将个人贷款视为一行业,各行业对应序号见附表2)、12个宏观指标和7个中债指数数据(2005年—2019年).其中部分中债指数发布较晚,数据从公布日开始.

附表1 银行及其对应序号

附表2 行业及其对应序号

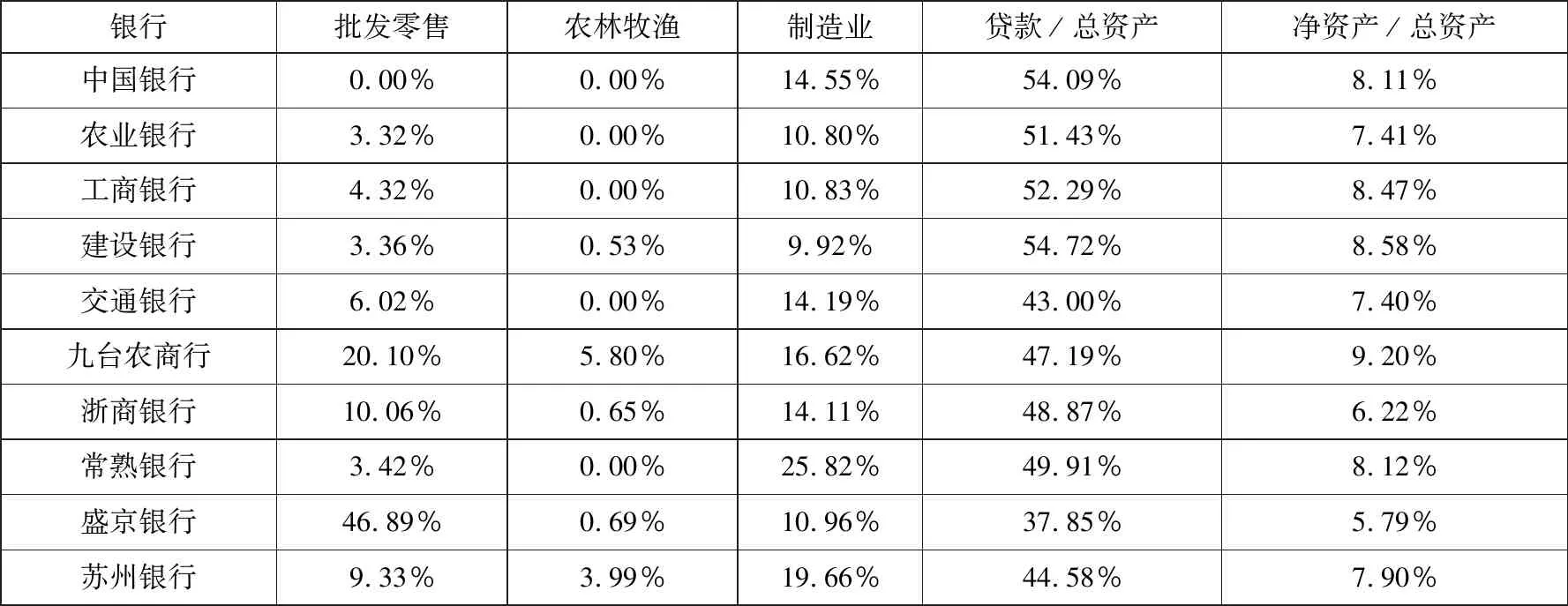
表2 各银行在高违约率行业贷款额占其总贷款额的比例

对单个银行,按行业分类得到银行对各行业的风险敞口,用Wind公布的各行业不良贷款率近似代表各行业的贷款违约率(可能会高估贷款损失,但目前尚无更合适的数据).

系统性风险分析的时间跨度不宜过短,但是时间跨度太长又会导致样本数据不足,因此本研究选取时间跨度为季度.由于各行业贷款违约率只能获得年度数据,季度违约率数据通过插值得到,具体做法:首先通过相邻两年违约率数据取平均得到半年度违约率,然后通过相邻的半年度违约率取平均得到季度违约率.

2.2 参数设定

根据文献一般做法,本研究将金融投资资产的逆需求函数设定为负指数函数的情形

pj=fj(ηj)=e-ajηj,j∈{1,2,…,m}

其中aj刻画了金融资产j变卖数量对其价格的影响程度,即资产j的流动性,其值越大则流动性越差.由于无法获得各银行金融资产的持有数量及价格相关信息,本研究将报表中相应资产的价值作为资产的持有数量,相应地设定资产的初始价格p0=(1,1,…,1)T.简便合理起见,后续研究中设定a1=a2=…=am=a,并分别考虑资产流动性a=0、1、2、3四种情景.特别地,当a=0时,表明资产流动性很强,不存在资产折价出售现象,即资产重叠不会引发价格传染效应.考虑外部资产重叠引发的价格传染效应时,可通过a的不同取值反映不同资产流动性水平对系统性风险的影响.图4给出了不同流动性状况下资产变卖比例与价格变动比例之间的关系.易见a越大,资产价格随着变卖比例增加下降越多.以a=2为例,当资产变卖比例达到一半时,价格大约下降到原来的一半.

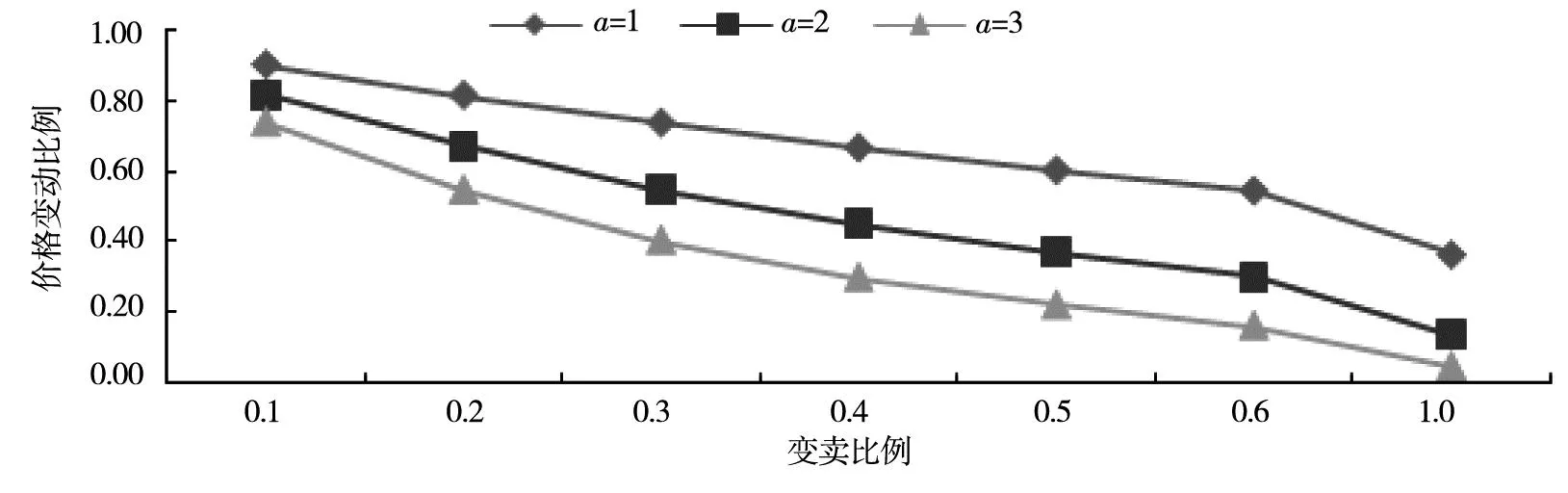
图4 变卖比例与价格变动比例之间的关系

对于内部相互借贷网络的恢复,参考Boss 等[37]及Gandy 和 Veraart[41]等以往文献研究结论,本研究将相应参数设置为:α=-1.5,β=0.25,γ=1,相应的先验分布参数设定为:ζ～U(0.5,2),ξ～Exp(1 000).实际上,模拟研究表明该参数的合理变化对网络形态影响较小.图5给出了两组不同参数下随机生成的两个网络样本,二者结构近似.其中46号银行是为了保证银行内部相互借贷数据平衡,特加入的虚拟银行(可看作是所有其它银行的综合).圆圈大小代表与对应银行有债务往来银行的多少,越大则表明与该银行存在债务往来的银行越多.从图可以看出,建设银行(12)、工商银行(4)、交通银行(16)、农业银行(22)、邮储银行(35)和中国银行(41)在银行体系中占据重要地位,与较多的银行存在往来,其中涵盖了我国的五大行,符合我国的实际情况.

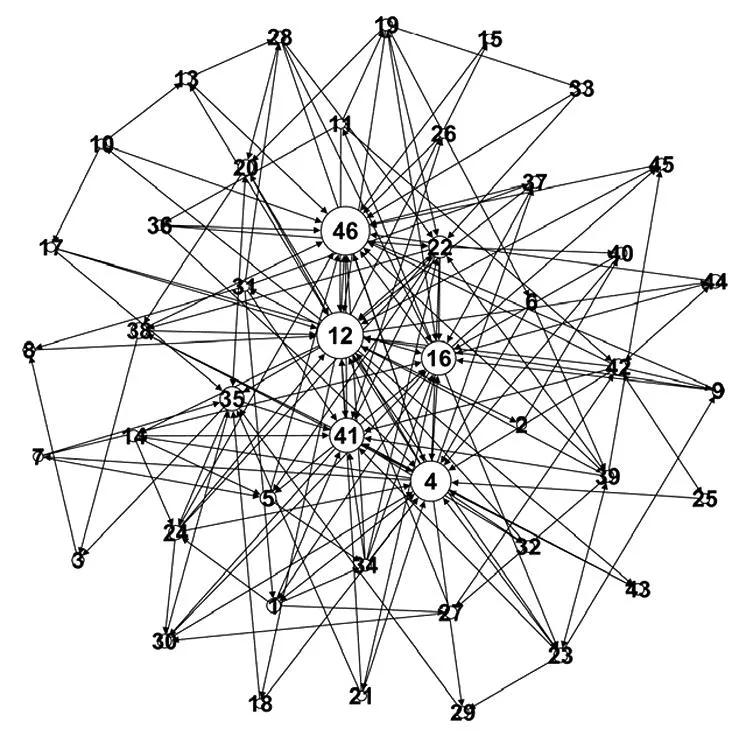
α=-1.5, β=0.25, γ=1

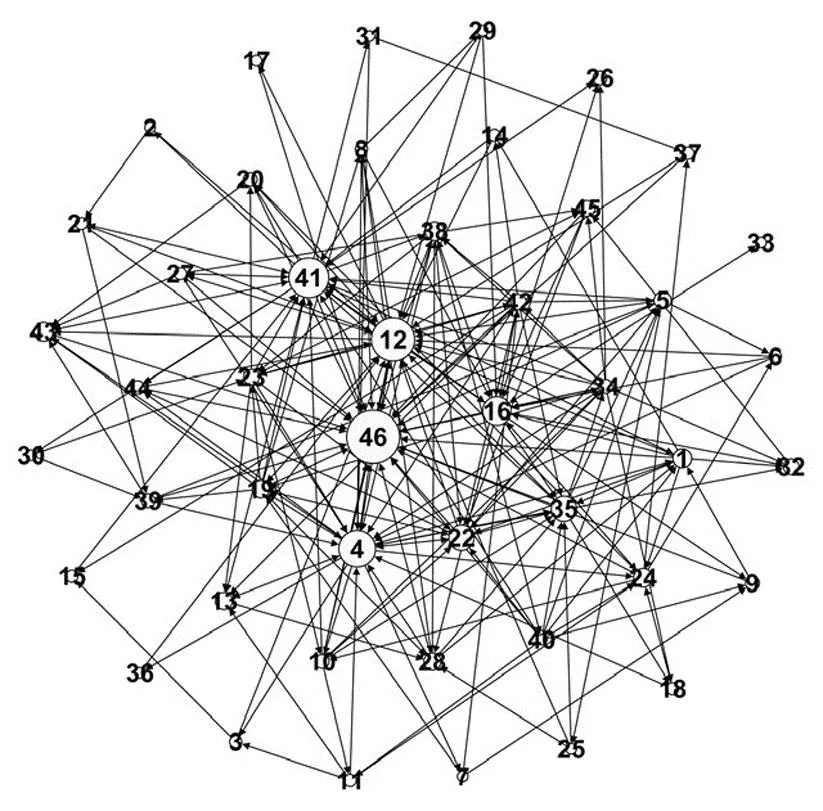
α=-2, β=0.1, γ=1

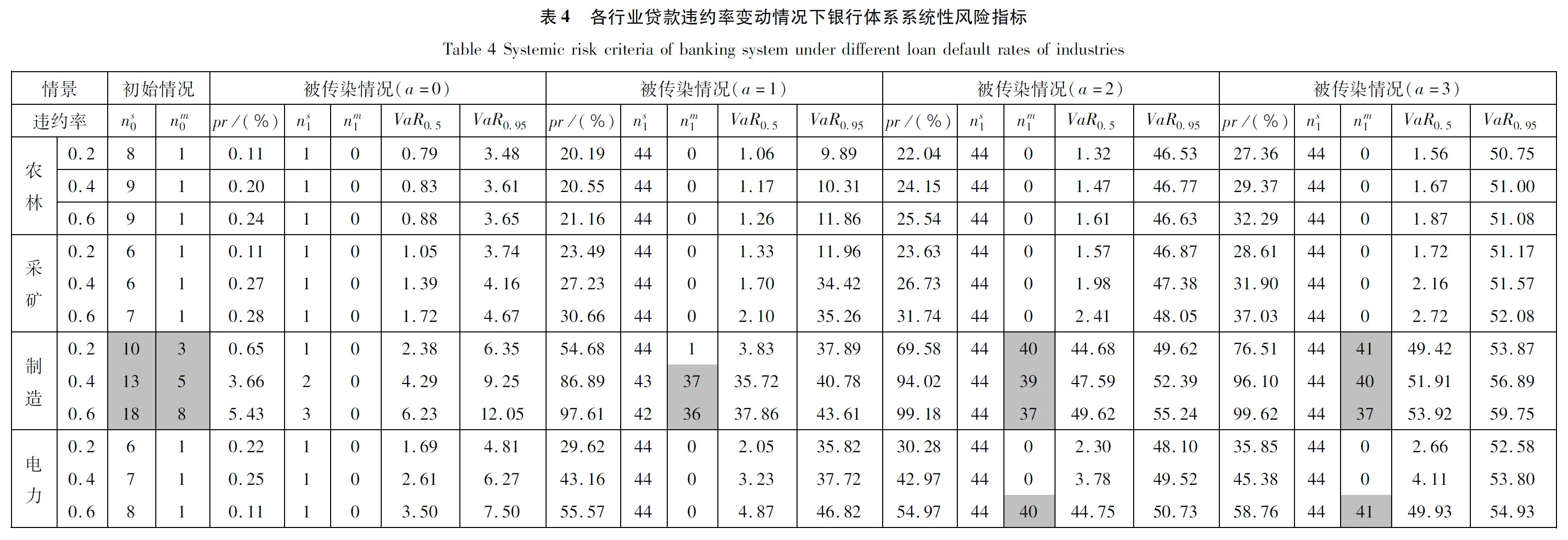
CreditRisk+模型中的输入信息为各行业贷款违约率的均值、标准差及相关系数.这些数据由2006年—2017年各行业贷款违约率历史数据求得.后续贷款违约率压力测试分析中,只改变各行业贷款违约率的均值.

2.3 情景分析与压力测试

目前,我国银行体系整体处于相对稳定的状态,但不稳定因素依然存在.银行体系贷款在行业上比较集中,金融投资资产重叠严重,宏观经济下行压力较大,这些都有可能成为银行体系系统性风险爆发的诱因. 为进一步分析贷款违约、金融投资资产价格变动及相关宏观因素变动对系统性风险的影响,本研究在2018年我国商业银行资产负债结构下,分别对行业贷款违约率、金融投资资产价格及宏观因素进行情景分析与压力测试.据此对我国银行体系系统性风险状况进行测评,旨在对未来可能引发银行体系系统性风险的重要行业、资产及关键因素进行分析探究.

2.3.1 历史情景分析

由相应中债指数数据可以看出,我国债券市场较为稳定,基本上不存在价格变动.由此历史情景分析时假定金融投资资产初始价格不变,仅考虑历史可能的贷款违约率情况下我国银行体系系统性风险状况.

1)历史贷款违约率分析

2006年—2017年我国各行业历史贷款违约率如图6所示.由于我国宏观经济环境变动,各行业贷款违约率也随之变动,主要经历了三个阶段:2006年—2007年,前期投资过热导致这一阶段违约率偏高;2008年—2012年,四万亿刺激,政策宽松,加之贷款基数大,贷款违约率出现下降;2013年至今,经济增速放缓,金融市场扩大开放,各行业贷款违约率有小幅上升.其中,农、林、牧渔业贷款违约率在2006年、2007年异常高.

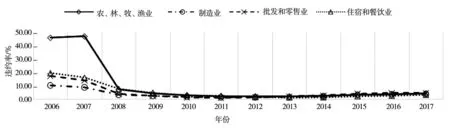
图6 各行业历史违约率

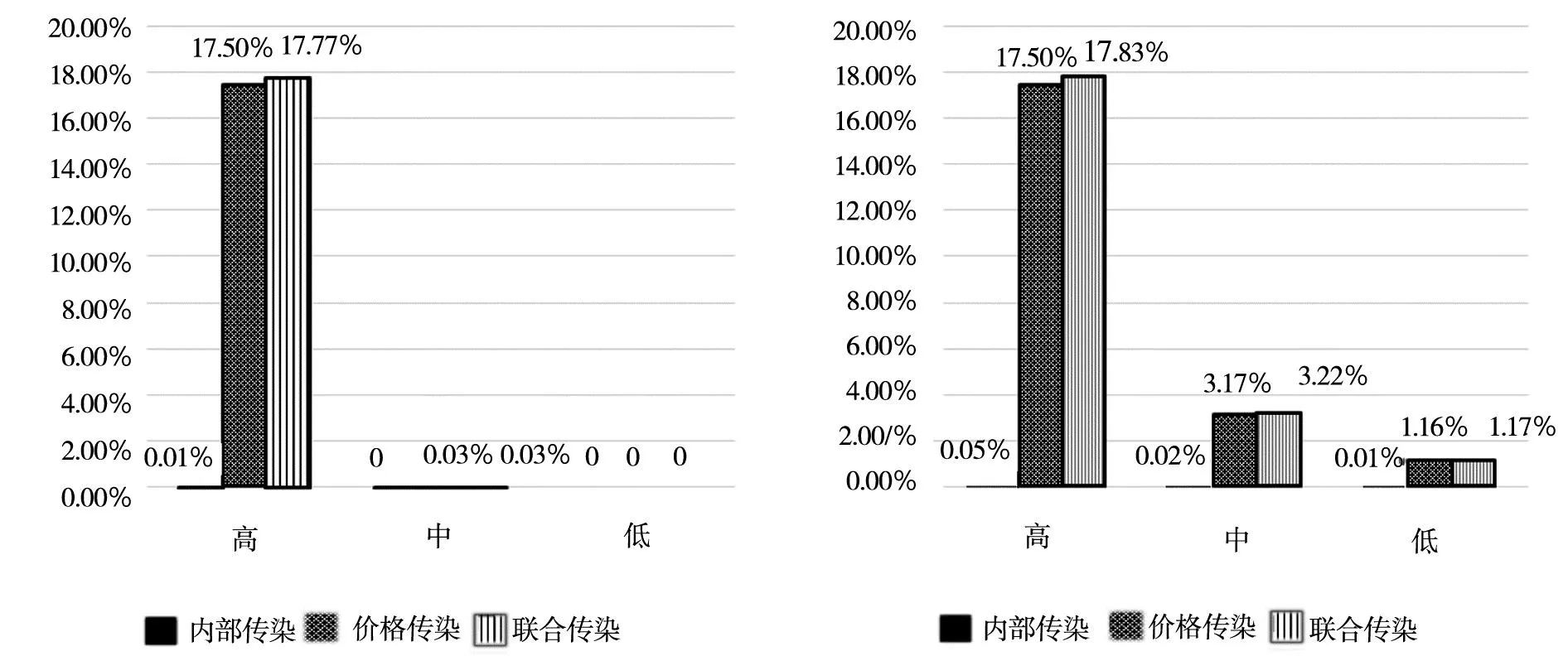
分别将2006年、2017年及2012年各行业贷款违约率作为贷款违约率高、中、低历史情景带入模型,对我国当前银行体系系统性风险进行评估,图7给出了各银行初始破产的概率.易见只有在违约率高的情况下,各银行在现有的资产负债结构下初始破产概率较高,银行体系处于相对不太稳定的状态,而其它情况下45家银中只有规模较小的九台农商行和浙商银行的破产概率超过5%,国有大银行破产概率均较低,银行体系整体较为稳定.

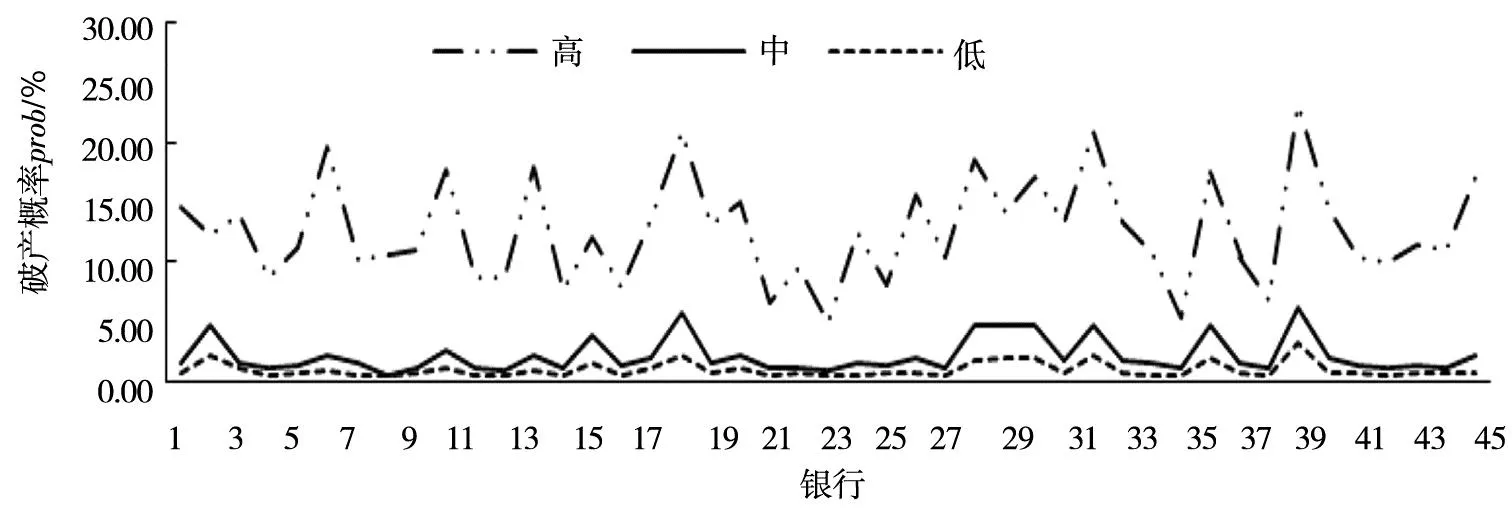
图7 历史情景下仅考虑贷款违约时各银行初始破产概率

由于风险主要来源于贷款损失,为探究小银行不稳定的原因,本研究对比分析了以九台农商行、浙商银行等为代表的小型银行与工商银行等五大银行的贷款结构.对近5年贷款违约率取均值,得到贷款违约率由高到低的前3个行业依次为:批发和零售业、农林牧渔业和制造业 (平均贷款违约率依次为:3.77%、3.28%、3.12%).表2展示了各银行对违约率前3的行业的贷款额占其总贷款额的比重、贷款占总资产的比重以及净资产占总资产的比重.从表可以看出,大银行在贷款违约率高的行业贷款额占其总贷款比例较低,而小型银行在违约率高的行业贷款占其总贷款的比重较高.显然,小型银行面临更高的违约风险.究其原因,一方面是信用相对较好的企业可能更容易获得大银行的贷款服务;另一方面,小型银行也可能有追求高收益动机,而将贷款贷向违约风险相对较高的企业,以获取更高的风险溢价.

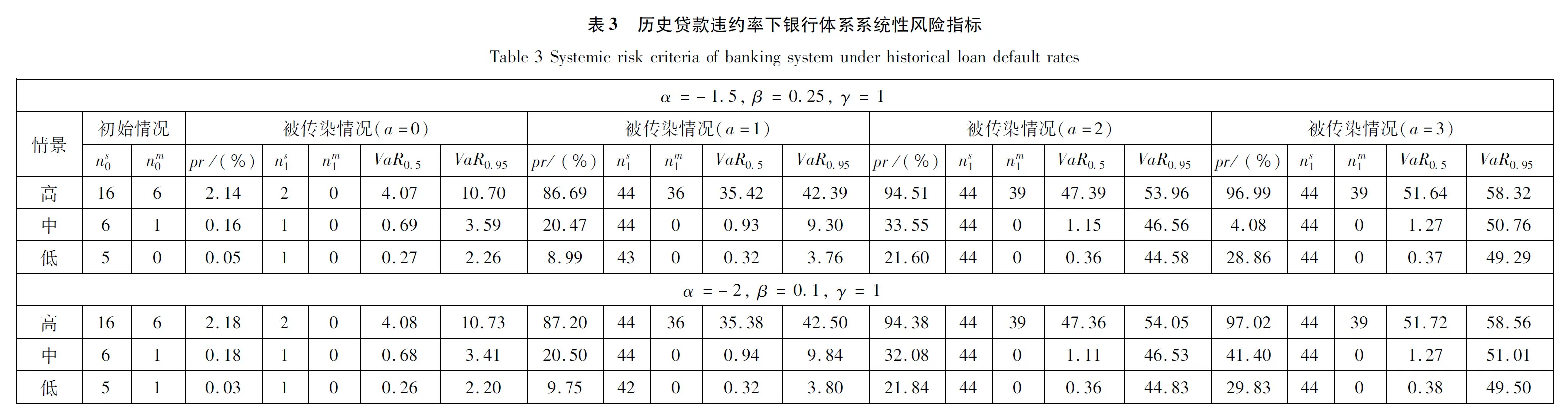
考虑历史情景下银行体系系统性风险指标的具体情况如表3所示.各银行在当前的资产负债结构下,随着行业贷款违约率上升,银行体系中初始破产银行数随之上升.仅考虑银行内部相互借贷产生的信用违约传染(a=0的情形,无价格传染)时,传染效应低,对系统性风险的影响不大.当银行内部相互借贷违约传染与资产重叠价格传染共同作用时,银行体系系统性风险被急剧放大,且随着资产流动性的降低(a的上升),系统性风险越发严重.

2)传染机制分析

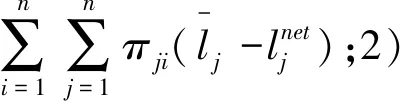
中位数 95%分位数

综上,资产重叠是我国银行体系目前潜在系统性风险传染的主要渠道,相互借贷网络在系统性风险传染的过程中起到加成的作用.但值得注意的是,在系统性风险传染的过程中,内部相互借贷对银行体系系统性风险的影响不容忽视.特别地,当银行体系内部相互借贷数额占总资产或总负债数额的比重较高时,内部相互借贷网络对系统性风险的传染效果会加剧[12,31].一旦存在银行破产便会发生内部违约,内部违约造成的相关银行资产损失势必加剧其流动性不足甚至破产,从而低价出售其资产并进一步加剧资产重叠价格传染效应.

为了考察银行内部借贷网络差异对系统性风险的影响,此处将网络恢复中参数另行设置为α=-2,β=0.1,γ=1,并与前述参数α=-1.5,β=0.25,γ=1情形下的结果进行对比.结果如表3所示,表明不同网络结构对风险传染的影响主要体现在被传染银行的个体差异上,而破产银行数量和整体资产损失并无显著差异.因此,后述内容不再考虑不同网络结构的对比分析.

2.3.2 贷款违约率压力测试

为识别出系统性关键行业,此处考虑行业违约率变动(其它保持不变)对银行体系系统性风险的影响.

1)单个行业贷款违约压力测试

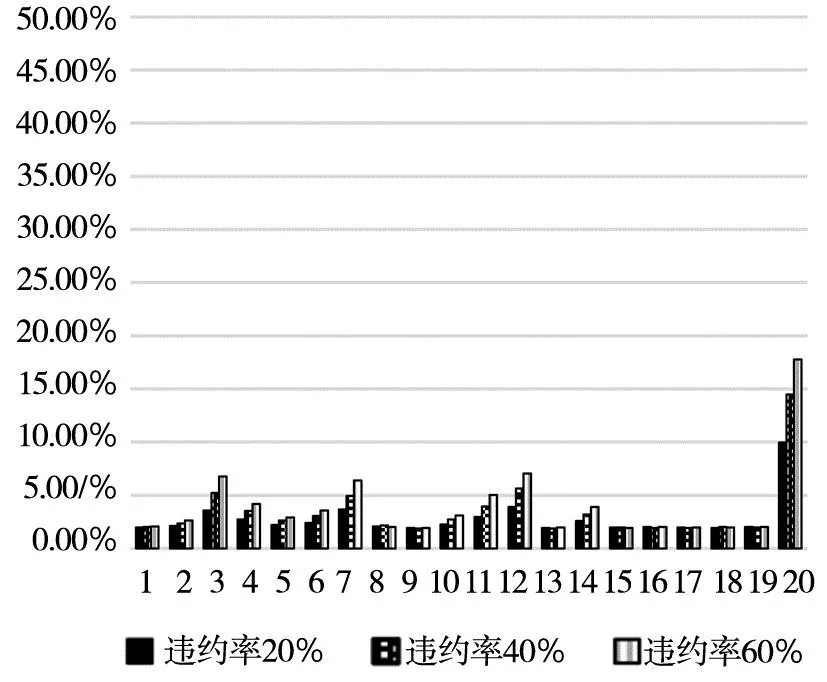
本研究以2017年各行业违约率为基准,分别将各行业的违约率调整为20%、40%或60%,得到单个行业违约率改变情况下银行体系系统性风险测度指标(汇总如表4所示).相应地,图9～图11分别展示了初始破产银行数的中位数及最大值和银行体系资产损失一般水平值及极端情况值占银行体系总资产的比例.在20个行业中,相较于其它,个人(贷款)、制造业、批发—零售业、租赁—商务服务业、水利—环境—公共设施管理业、房地产业、交通运输—仓储—邮政业等7个行业违约所造成的初始破产银行数量较多, 且随着违约率上升,初始破产银行数急剧上升,流动性匮乏时可能导致所有银行破产.当资产流动性良好时,内部相互借贷网络对风险的传导并不明显.但是,内部相互借贷违约传染与资产重叠价格传染共同作用时,被传染银行数量及银行体系资产损失值急剧上升,且流动性越差(a越大)传染效应越大,银行体系损失也越严重.值得指出的是个人贷款对风险的贡献比较大,即使在流动性较好的情况下亦如此.在流动性匮乏的情况下(a=2、3),制造业、房地产业、租赁和商务服务业以及个人贷款等单个行业违约率达20%时,会导致整个银行体系损失一般水平占总资产的比例达30%左右.而当考虑极端损失的情况时(95%分位数),所有的行业都将达到这一水平.

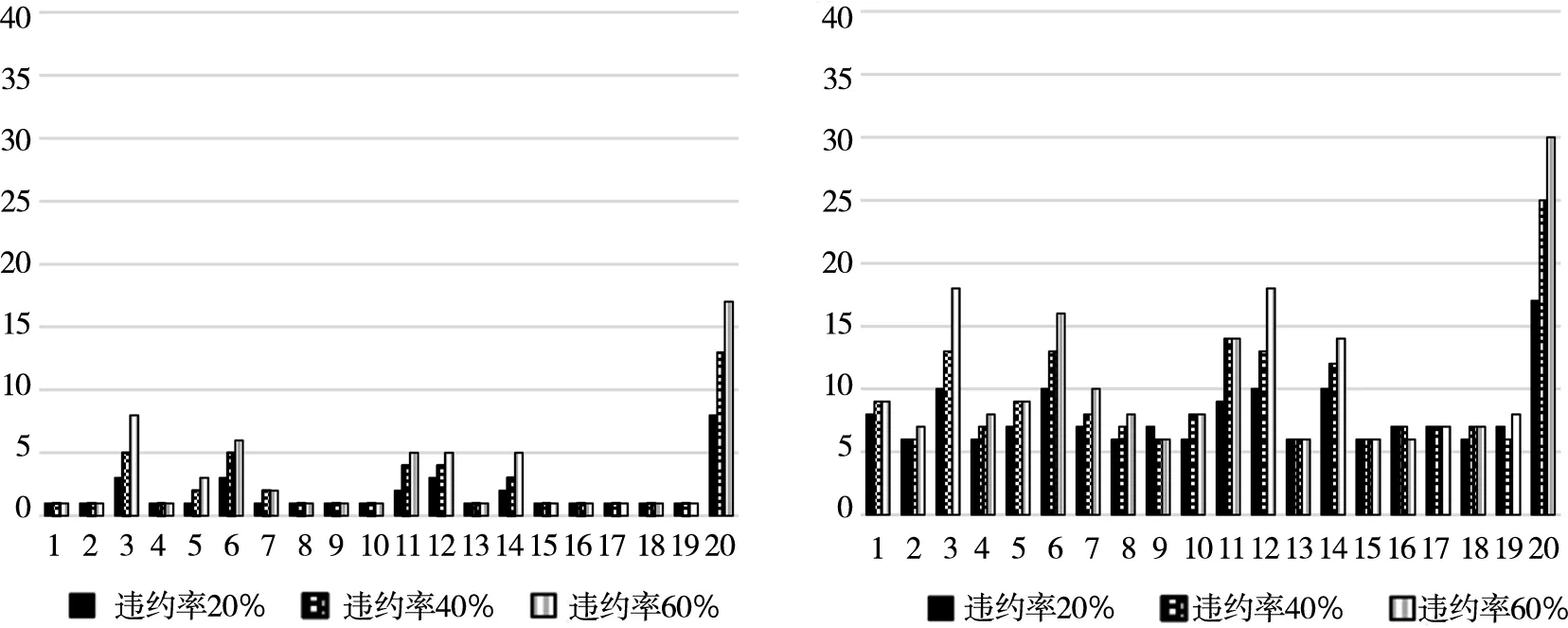
中位数 最大值

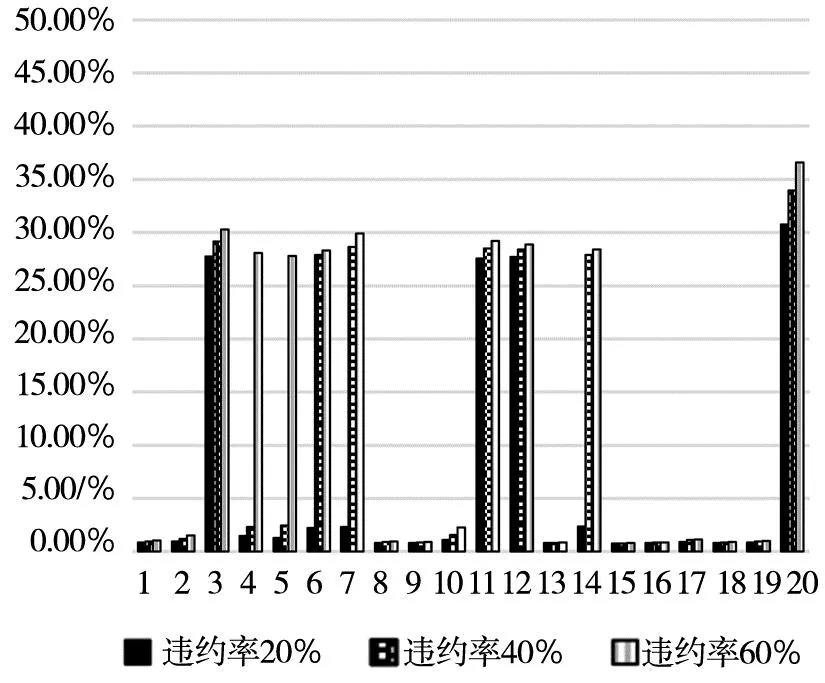
a=3

a=3

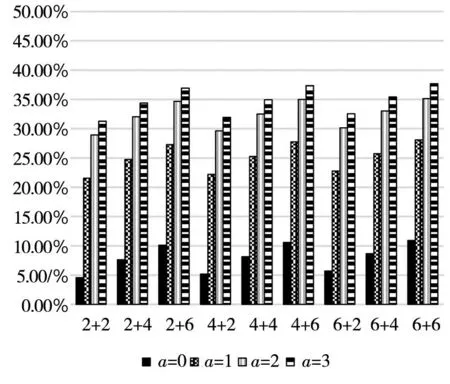
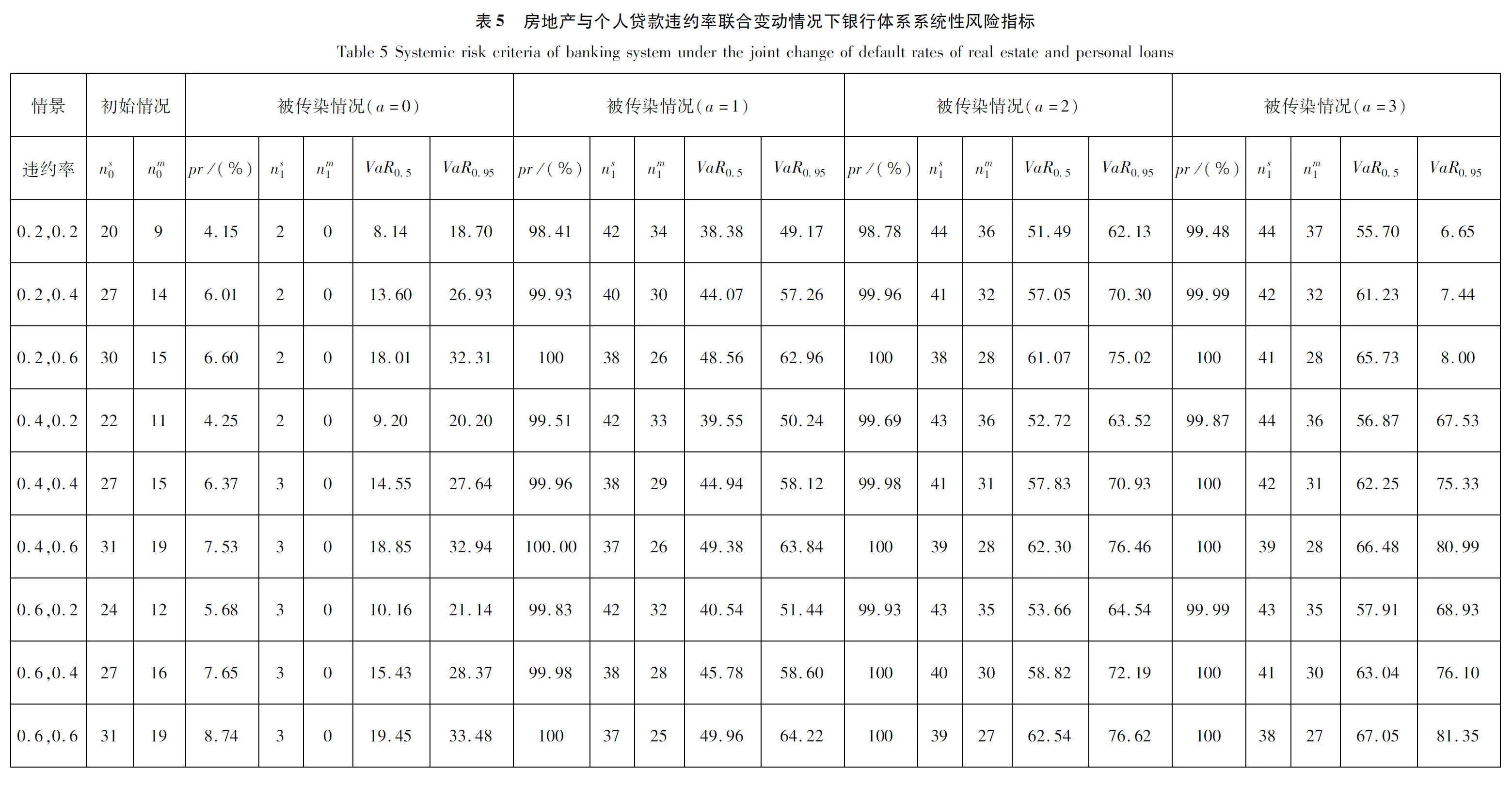
2)房地产业与个人贷款违约率组合压力测试

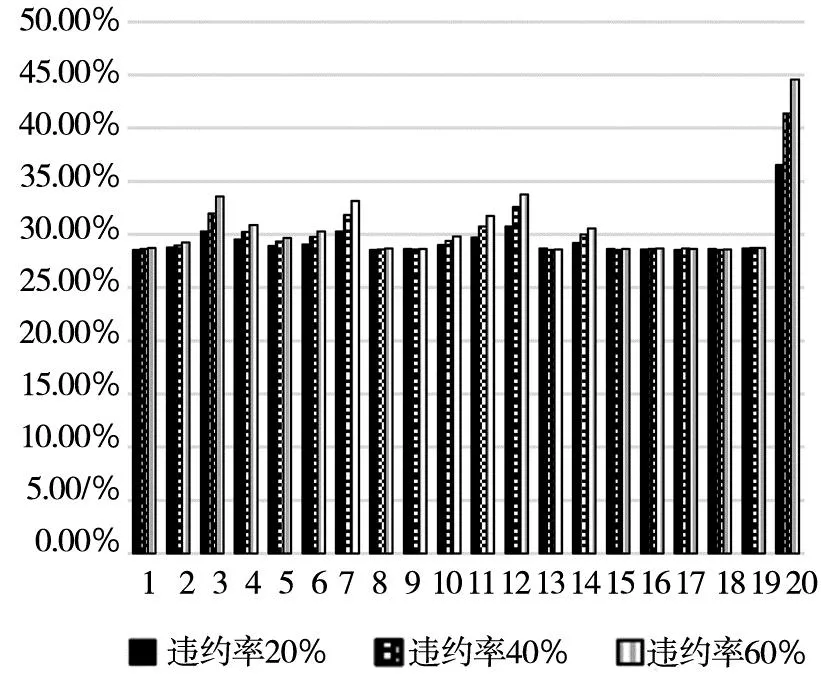
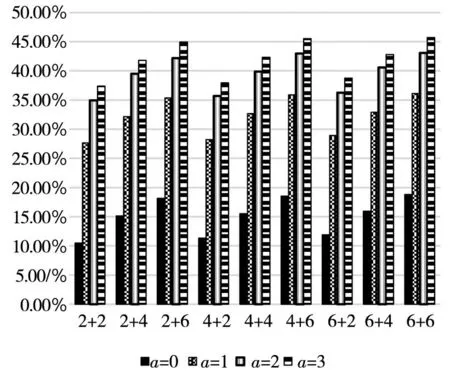
在我国银行体系贷款中,个人贷款主要包括了个人消费贷款及住房贷款,其中60%以上是个人住房贷款.因此个人住房贷款与房地产业紧密相关.由此,为进一步探究房地产市场波动对银行体系系统性风险的影响,本研究考虑房地产业及个人贷款违约率同时上升时整个银行体系系统性风险的状况.如表5所示,可以看出当房地产业与个人贷款违约率同时达到20%时(图中用2+2表示,余下的类推),系统中初始破产银行数中位数便达到9个,加之传染的影响,最终所有银行都可能破产,整个银行体系会出现系统性崩溃.图12给出了对应违约率下初始破产银行数的中位数及最大值.图13给出对应违约率下银行体系资产损失一般水平值及极端情况值占总资产的比例,由此也可进一步看出房地产市场波动导致的损失加上银行体系相互借贷违约传染和资产重叠价格传染可能造成我国银行体系高达40%以上的资产损失.房地产市场的稳定性不容忽视,对房地产市场的监管依然是系统性风险防控的重点.

a=0

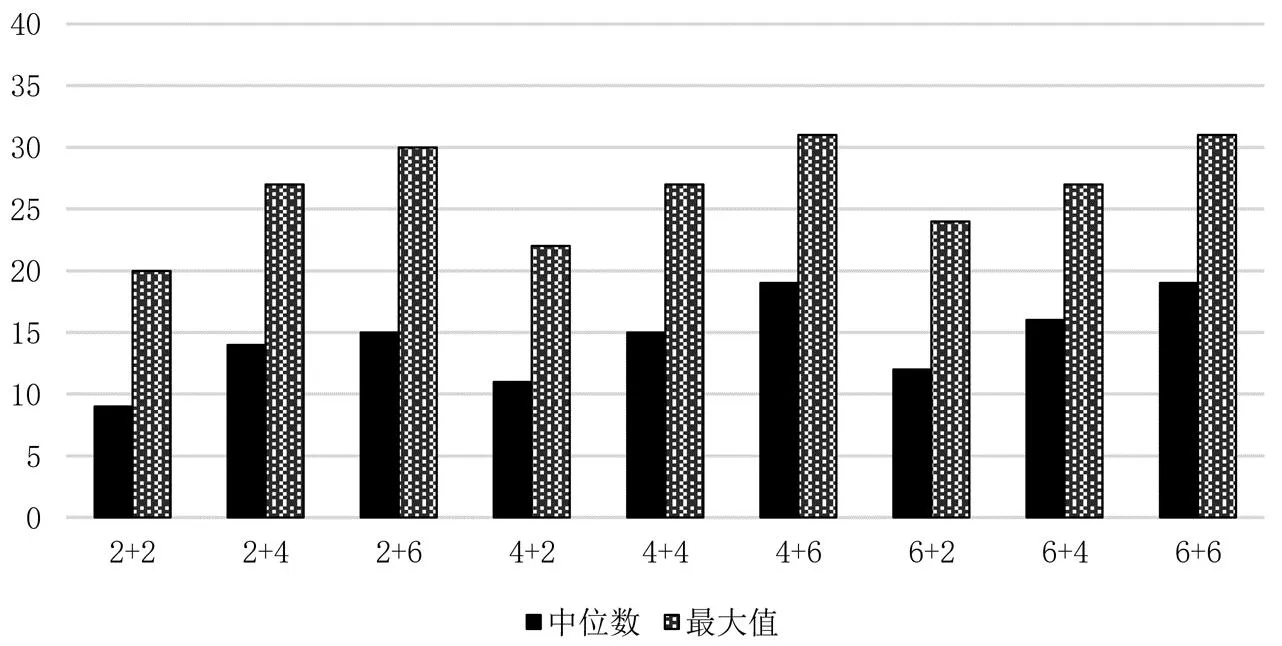
图12 房地产业与个人贷款违约共同作用下初始破产银行数

VaR0.95

2.3.3 金融资产价格压力测试

假设无贷款违约发生的情况下,模拟结果表明,在金融投资资产(主要是债券)所有可能的历史价格水平下,没有银行因为金融资产价格变动而发生初始破产.究其原因是由于我国债券市场发展较晚,债券市场不存在大幅波动.因此,需要指出的是,本部分未对债券价格进行随机抽样,而直接对价格进行压力测试.风险评估样本完全由10 000次银行相互借贷网络抽样决定.

为分析各类金融资产价格变动对银行体系系统性风险的影响,从而识别出系统性关键资产,本研究分别考虑各类金融资产价格由1变为0.6、0.4、0.2(即折价40%、60%、80%),而其它金融资产价格保持不变时,单类金融资产价格单项变动对银行体系系统性风险的影响.结果如表6所示,由于不考虑资产价格的波动性,模拟结果差异很小,由此表中仅展示各风险指标的中位数.图14给出了各类资产价格变动引起的初始破产银行数. 图15给出了各类资产价格变动所引起的银行体系资产损失一般水平值占银行体系总资产的比例. 可以看出,地方政府债券、同业及其金融机构债券及委托理财投资相比其它金融资产对银行体系系统性风险的影响较为显著,当资产价格下跌幅度加大时,这几类资产对银行体系系统性风险的影响均明显加剧.其它资产价格变动对银行体系系统性风险的影响不明显.当资产流动性很好时(a=0),内部相互借贷违约传染效应并未发生,此情况下银行体系资产损失也很小.在由地方政府债券、同业及其它金融机构债券或者委托理财投资价格变动引发初始破产的情况下,内部相互借贷违约传染与资产重叠价格传染共同作用导致被传染银行数量及系统资产损失值急剧上升.通过对比前述贷款违约率变动带来的损失与金融资产价格变动带来的损失可以看出,前者对我国银行体系系统性风险的影响较大.

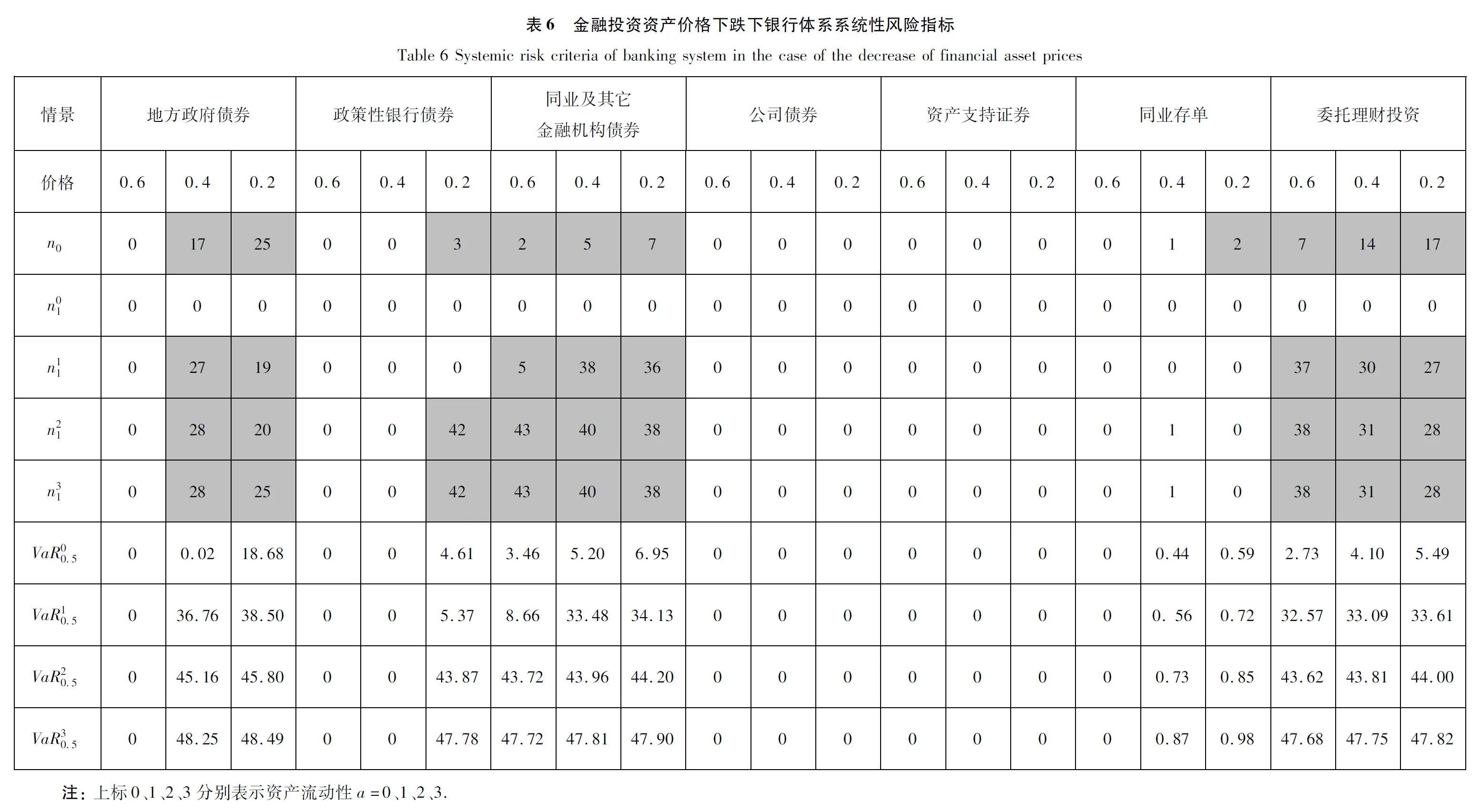
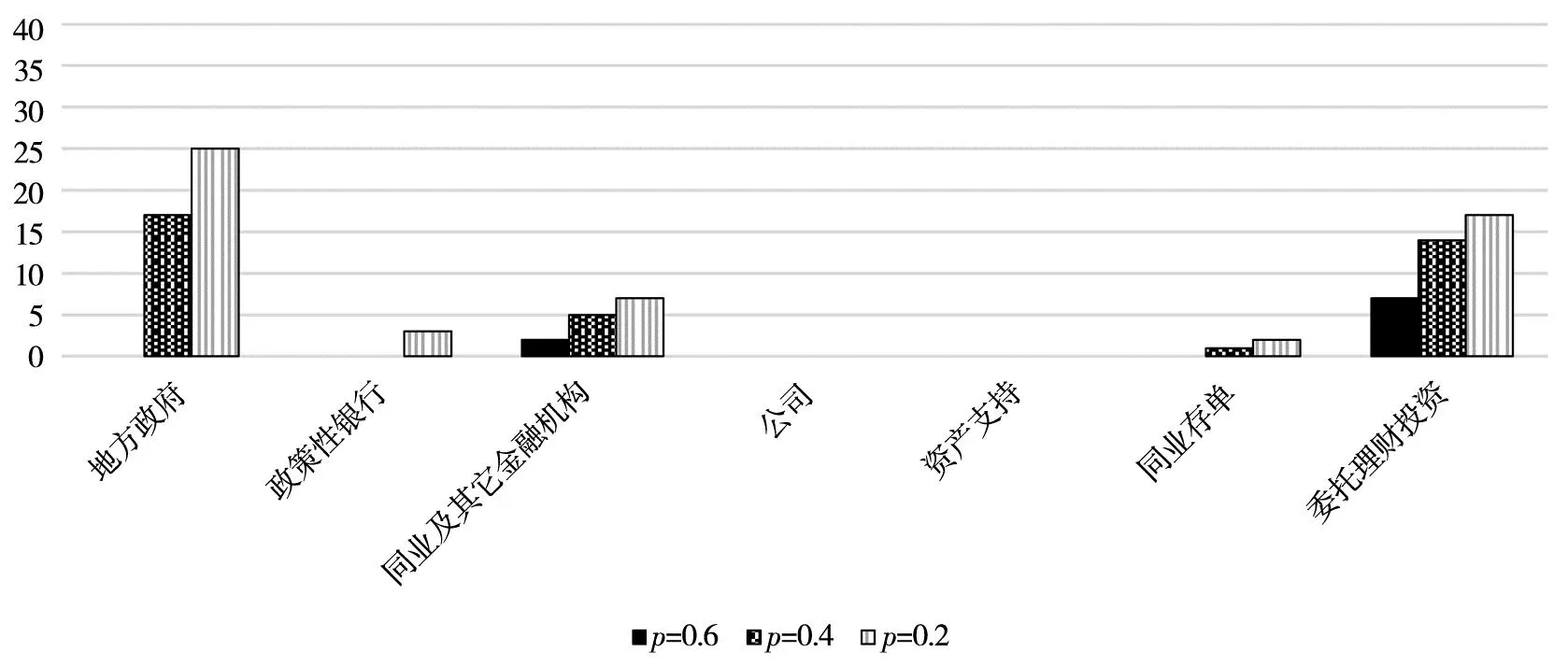
图14 金融资产价格下跌下初始破产银行数量

a=3

2.3.4 宏观因素压力测试

通常,贷款违约与金融投资资产价格之间存在一定的相关性.为准确测度系统性风险,本节通过宏观公共因子将行业贷款违约率与金融资产价格(债券)的联合变动有机地结合起来,考虑二者对我国银行体系系统性风险的联合影响. 相关结论也可为防范系统性风险的宏观策略制定提供借鉴.

1)宏观因素对贷款及贷款违约率及债券价格的影响.

对于宏观变量与贷款违约率之间关系的研究,已有文献所选的宏观变量存在一定的差异.Bonfim[49]选取GDP及GDP增长率、出口量、私人消费、固定资本增长率、失业率、汇率、贷款增长率、国债收益率斜率、利率以及股市收益率等宏观变量进行分析.结果表明,在剔除不显著变量以及符号不符的变量后,利率、收益率曲线斜率、贷款增长率、股市收益率和GDP增长率对企业破产违约具有显著影响.Bofondi和Ropele[50]在研究宏观变量对意大利银行不良贷款率的影响时选取GDP增长率、失业率、CPI、利率、债务负担、房价增长率、股市增长率、国债收益率曲线斜率等宏观变量.用分组后的宏观变量与不良贷款率进行回归表明失业率、GDP增长率、利率和房价增长率为解释变量时模型的拟合效果最好.Figlewski等[51]将宏观变量分为三类:宏观状态相关的变量(失业率、通胀率、经济前景指数等)、经济趋势相关的变量(GDP增长率、消费者情绪变化等)和金融市场相关变量(利率、股市收益率等).将所有宏观变量放入模型时,只有消费者情绪变化、股市收益率显著.剔除显著性最差的变量后,结果表明消费者情绪、长期国债利率、股市收益率在回归中可以同时显著.

有鉴于此,为避免遗漏重要的宏观变量,本研究综合选用GDP增长率、金融部门杠杆率、非金融企业部门杠杆率、居民部门杠杆率、地方政府杠杆率、CPI、失业率、上海同业拆借利率、上证指数增长率、房价增长率、M2增长率和国债收益率曲线斜率等变量作为宏观经济变量,其中,各部门杠杆率是各部门债务与GDP的比值.利用这些变量分析宏观经济对贷款违约率、信用利差和期限利差的影响.

为尽可能全面利用各宏观变量中隐藏的贷款违约率相关信息且规避各宏观变量之间的相关性,本研究利用因子分析方法降维后得到的因子与贷款违约率、信用利差、期限利差分别回归.当回归不显著时则剔除不显著因子中对应权重大的变量,最后发现GDP增长率、地方政府杠杆率、居民部门杠杆率、金融部门杠杆率和非金融企业部门杠杆率构成的宏观因子(Eco)与贷款违约率、信用利差与期限利差之间存在显著的关系.因子(Eco)总方差解释占比为83.05%,其载荷及成分系数矩阵如附表3 所示.由因子载荷可以看出各部门杠杆率的因子载荷近似为1,而GDP增长率为-0.61,从成分系数可以看出,因子得分与各部门杠杆率正相关,与GDP增长率负相关.因子中各个变量的成分系数与其均值和标准差结合,可得因子得分为

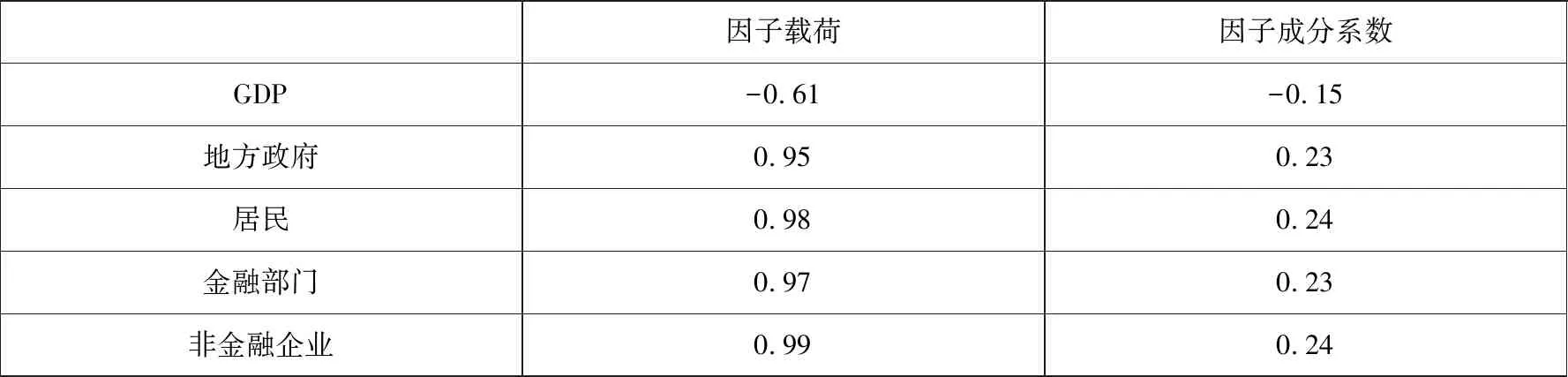
附表3 宏观因子载荷及成分系数

Ecot=-1.74-6.94GDPt+3.35govt+

1.74ret+1.24fst+0.96but

其中GDP为GDP增长率、gov为地方政府部门杠杆率、re为居民部门杠杆率、fs为金融部门杠杆率、bu为非金融企业部门杠杆率.由此可以看出各变量绝对水平变动对宏观因子的边际影响从大到小依次为:GDP增长率、地方政府部门杠杆率、居民部门杠杆率、金融部门杠杆率、非金融企业部门杠杆率.

为排除2008年危机后我国采取宽松的财政政策和货币政策对贷款违约的影响,本研究选用从2013后的数据分析宏观因子与贷款违约率之间得关系,图16展示了按行业贷款头寸加权的平均违约率与宏观经济因子之间的关系.从图可以看出宏观环境越好(各部门杠杆率低、GDP增长率高),贷款违约率越低,这与以往文献研究中的结果一致.考虑各行业间存在差异,本研究利用固定效应面板数据回归分析宏观因子与各行业贷款违约之间的关系如附表4所示.回归系数均在5%置信水平下显著,说明宏观因子与违约率之间存在显著的相关关系.从回归系数可以看出宏观因子与违约率之间正相关.

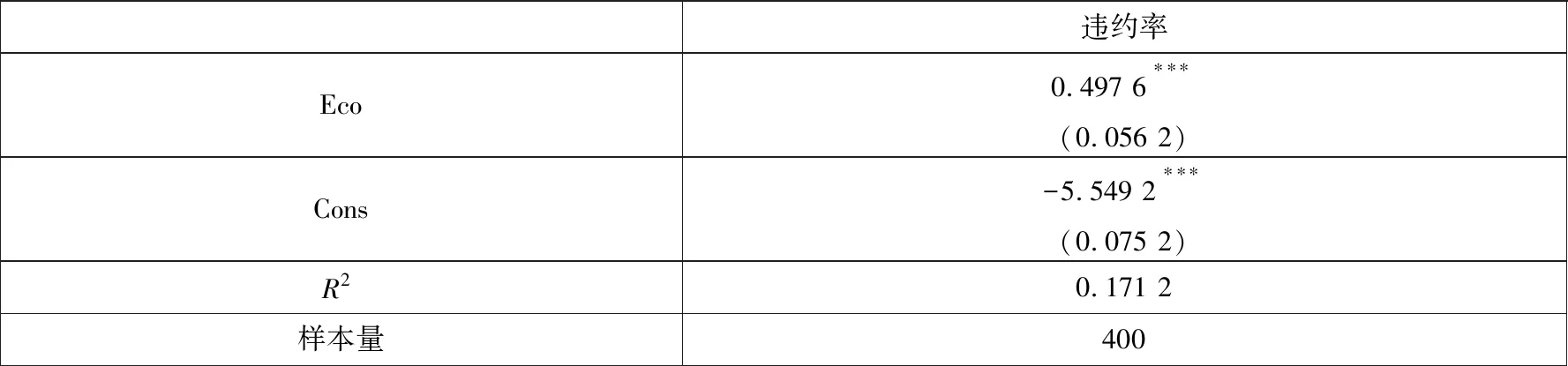
附表4 宏观因子与行业贷款违约率的回归

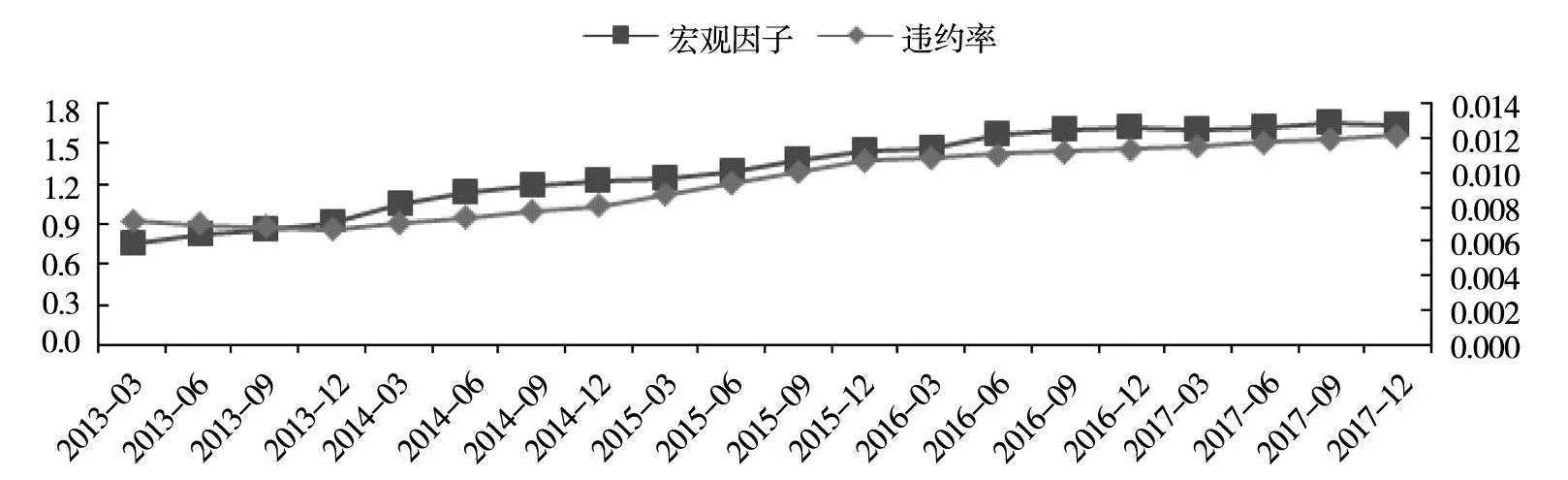
图16 宏观因子与平均违约率

本研究的信用利差为企业债市场组合的到期收益率与相同期限的国债到期收益率之差,期限利差为与企业债市场组合期限相同的国债到期收益率与1月期国债到期收益率的差.其中,企业债市场组合用中国债券信息网的中债—公司信用类债券指数组合衡量.由于市场组合到期期限不是整数,因此,采用McCulloch[52]提出的三次多项式样条对国债到期收益率曲线进行拟合.考虑回归的稳健性,采用月度数据和季度数据分别进行回归,据此分析债券超额收益率与期限利差及信用利差之间的关系,结果如附表5所示.信用利差及期限利差与宏观经济因子(Eco)的回归结果如附表6所示.

附表5 债券期望收益率与信用利差, 期限利差

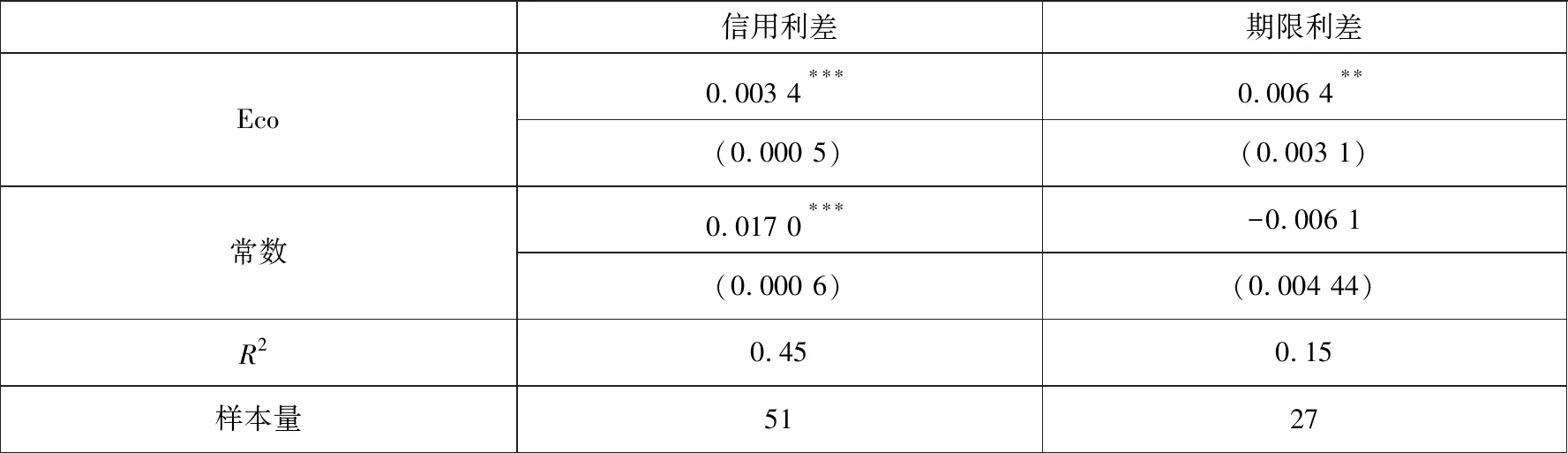
附表6 信用利差、 期限利差与宏观因子

由式(3)～式(6)及附表3～附表6可知,在经济正常发展时段(2013年—2017年),我国行业贷款违约率受到GDP增长率及各部门的杠杆率的影响,其中高GDP增长率可以降低各行业贷款违约率,而各部门高杠杆率会加剧各行业的贷款违约.对于债券价格,高GDP增长率可以降低信用利差及期限利差,由此推升债券价格,而各部门高杠杆率会促使投资者要求更高的信用利差及期限利差,进而降低债券价格.

2)基于宏观变量的压力测试

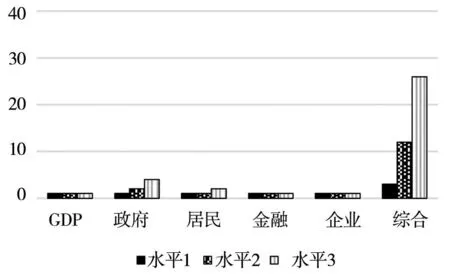
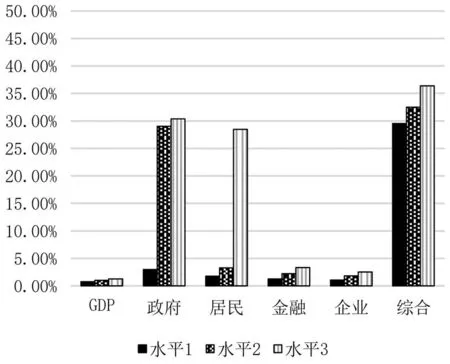
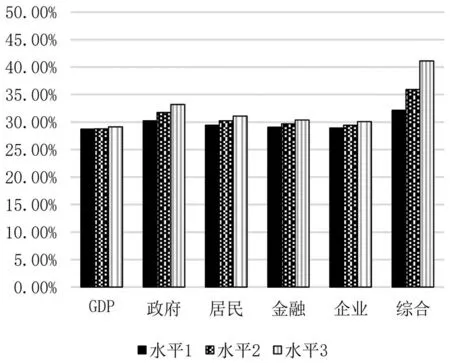
为探究GDP增长率、各部门金融杠杆率分别及联合变动情况下系统性风险的状况,本研究分析了不同GDP增长率及各部门杠杆率水平下银行体系系统性风险的情况.为简洁起见,设定如下三种情况:“水平1”表示GDP增长率下降到5%或者某部门杠杆率

在2018年的基础上上升20%;“水平2”表示GDP增长率下降到4%或者部门杠杆率在2018年的基础上上升40%;“水平3”表示GDP增长率下降到3%或者某部门杠杆率在2018年的基础上上升60%.

所得系统性风险压力测试结果如表7所示.从中可以看出,以2018年的宏观环境(GDP增长率和杠杆率)为基础进行的风险测度表明当前我国银行体系整体稳定,风险较小.但尾部风险仍然偏高,一旦有银行出现初始性破产,加之资产流动性不足,有爆发系统性风险的可能.图17给出了不同GDP增长率水平及杠杆率水平下初始破产银行数目,图18～图19分别给出了宏观因子变动所引起的银行体系资产损失一般水平值及极端情况值占银行体系总资产的比例.由此可以看出地方政府杠杆率的升高对银行体系系统性风险的影响较大,居民杠杆影响亦不可忽视.单独看GDP增长率的影响发现其影响并不大,但GDP对系统性风险的影响不应只单独考虑其单一变动的结果.由于各部门杠杆率是各部门债务与GDP的比值,若保证各部门债务增长率不变,GDP增速下降将导致各部门杠杆率上升.因此,应当考虑GDP增长率下降与各部门杠杆率上升综合作用下系统性风险的情况.由图表中“综合”情景下银行体系系统性风险指标可以看出,即使在相对乐观的情况下(GDP增长率下降至5%,各部门杠杆率提升20%),初始破产银行数量的一般水平达到3,在资产流动性较好的情况下银行体系资产损失值一般水平超过系统总资产的20%,而在资产流动性差的情况下银行体系资产损失的一般水平接近系统总资产的30%,通过传染所有的银行可能同时破产.由此可以看出,目前稳定GDP增长率水平不仅只是为了保证发展经济本身,也是防范金融体系系统性风险的有力举措.

中位数

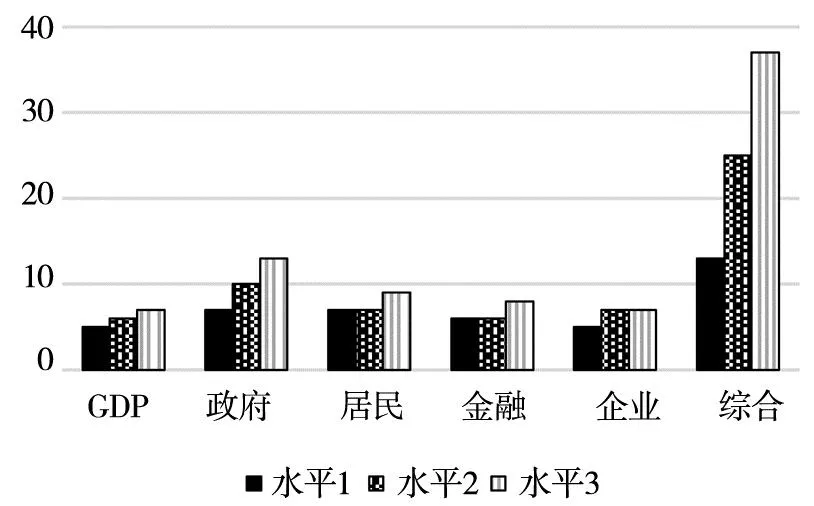
最大值

a=3

a=3

3 结束语

现阶段我国银行体系比较稳定,但目前经济形式复杂,金融体系系统性风险潜在诱因犹存并不可小觑.本研究所提出的系统性风险测评模型,合理地将我国银行体系实际情况与各类风险测度模型相结合,为我国金融体系系统性风险测度与评估提供了一个可供参照的量化分析框架.在此基础上,全面地分析评估了现阶段我国银行体系潜在的系统性风险状况.尽管如此,由于数据限制和模型简化原因,该评估不可能做到完全准确地反映真实情况,但所得研究结论对现实仍可提供有价值的参考.以下对相关研究结果进行简要总结并提出相应政策建议.

本研究发现主要包括如下四个方面.

1)系统性风险传染渠道及效应:当资产流动性较好时,仅考虑银行内部相互借贷网络,银行体系系统性风险传染效应甚小.但是,综合考虑内部相互借贷引发的违约传染及资产重叠引发的价格传染时,银行体系系统性风险的传染效果非常明显,且随着资产流动性变差,风险传染的范围及带来的损失也随之变大.由此可知,我国银行体系的风险传导主要通过价格传染,借贷网络传染起到加成作用.资产重叠与资产流动性匮乏是引发系统性风险的主要机制与关键因素.

2)系统性关键行业:个人(贷款)、制造业、批发—零售业、租赁—商务服务业、水利—环境—公共设施管理业、房地产业、交通运输—仓储—邮政业违约率上升所引发的初始性破产银行数量相较于其它行业较大.由于贷款在这些关键行业的数额较大,且各银行间贷款重叠严重,若加之投资端债券流动性匮乏,即使单一的关键行业发生违约,便可引发银行大面积破产和资产重大损失.

3)系统性关键资产:地方政府债券、同业及其它金融机构债券以及委托理财投资资产价格下跌所引发的初始破产银行数量较多.资产重叠严重,若加之资产流动性匮乏的影响,单类资产价格变动便足以使整个系统崩溃.总体而言,相对于投资端,银行体系信贷端资产数额较大,对系统性风险的影响更大.

4)宏观方面,相较于其它因素,地方政府部门杠杆率过高和GDP增长率过低都会对我国银行体系系统性风险造成较大影响,居民杠杆影响亦不可忽视.

基于上述研究发现,本文对宏观监管和资本市场建设提出以下三方面建议.

1)严格房地产行业的监管:房地产业贷款、个人(贷款)、建筑业、委托理财投资和地方政府债券是银行体系系统性关键行业与资产,而它们均与房地产行业有直接或间接的紧密联系.房地产行业的稳定与否直接关系到这五部分相关资产的状况.为避免房地产行业波动对银行体系的影响,一方面应当严格控制银行体系向房地产行业的资金流出,从而减少相应风险暴露;另一方面应当稳定房价,避免房价大起大落从而引发系统性风险.

2)稳杠杆与稳增长:相较于其它部门杠杆,地方政府部门杠杆的上升对系统性风险的影响较大,居民杠杆亦不可忽视.单独看GDP增速下降对系统性风险的影响并不太明显,但是GDP增速下降可能会导致各部门杠杆的上升,警惕低经济增长与高杠杆共同作用引发系统性风险.

3)建设高信用水平金融体系和更具深度与广度的资本市场:银行体系是我国融资主体中介,且其主要金融投资资产是债券,银行体系的贷款违约主体与债券违约主体重合度高,因而面临巨大的信用风险.另外,资产流动性对系统性风险亦有关键性影响.信用风险、市场风险与流动性风险叠加将带来巨大的系统性风险.加强诚信教育和信用保证制度建设是完善我国金融体系的重要工作;广泛分散的投融资渠道(特别是直接投融资渠道),将起到降低银行体系系统性风险重要作用;建设更有深度(流动性强)和广度(投融资渠道多)的资本市场是有益且必要的发展方向.

既要预防系统性风险,又要保证各部门的融资需求,必然对我国银行体系运营管理提出更高的要求,银行需要“一放一收”地做好资金融通和风险管理工作.本研究对现阶段银行运营管理建议如下:一方面,在做好风险管理的情况下,放宽企业(特别是民营企业)的贷款准入标准,为实体经济输血,保障就业、促进经济发展.另一方面,审慎收紧在系统性关键行业和资产上的信贷与投资业务,做到资金投向明确、风险分散可控.特别地,在贷款端,应当更加严格把控贷款拨付标准,预防资金过于集中地投放于房地产等系统性关键行业;在投资端,应当更加重视债券发行人的财务和经营状况,做好风险评级工作.地方政府债券以及委托理财投资的资金投向应当给予特别关注.

最后,值得指出的是本研究仍然存在一些不足有待后续研究进一步改进和完善.首先,对于金融投资资产分类,由于无法获得相关风险资产的详细信息,比如相关债券的期限等,风险度量不可避免地存在一定误差.其次,银行体系内部相互借贷网络真实网络数据无法获得,任何数据恢复方法均可能存在偏差,从而导致风险度量误差.最后,在宏观因素与系统性风险的分析中,宏观因素与债券违约率、资产价格之间的关系由当前数据分析得到,当经济情形发生变化时,该类关系亦可能发生结构性变化,相应地,影响系统性风险的关键因素和影响程度均可能发生变化.

附录