解三角形中的困惑与策略

王永军

（重庆市广益中学校，重庆 400065）

在解三角形中，正、余弦定理具有核心、重要的作用，加之三角形面积公式、三角函数的变换等，构成了解三角形最基本的工具。

一、“误”解（困惑）与正解策略

（一）“误”用余弦定理

例1（2020年高考浙江卷）在锐角△ABC中，内角A、B、C的对边分别为a、b、c。已知。

（1）求B；

分析：本题条件简单、叙述清晰。（2）问在（1）问的基础上进行解答，B=；由锐角、内角和可得，对cosA+ cosB+ cosC进行变形，可变为；利用正弦曲线得到，于是所求取值范围为。下面重点探讨（1）问的求解。

1.“误”解（困惑） 用余弦定理化简求角

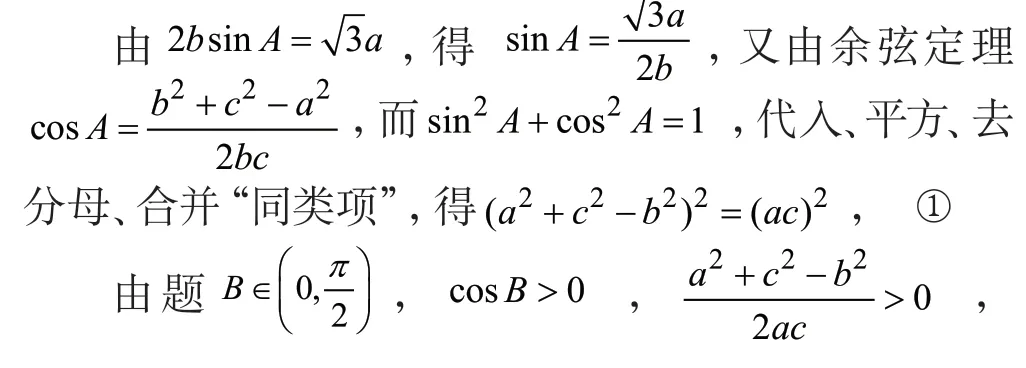
为了得到①式，这里虽然省去了详细的书写过程，但依然可以清晰想见化简、转化的“艰辛与痛苦”，很明显运算的过程很繁杂 而充满“技巧”（要不断向“目标”式子靠近），“一不小心”将“前功尽弃”。

2.正解 用正弦定理化简求角

这里全程口算。

遇见问题要三思而后行，所谓磨刀不误砍柴工。通过对比，繁简自知。

（二）平分秋色

例2 在△ABC中，内角A、B、C的对边分别为a、b、。

（1）求cosA；

（2）求c。

分析：本题条件简单、叙述清晰，是解三角形的常见题型，属于中档题。（1）问由正弦定理、三角函数的二倍角公式易于求得。下面探讨（2）问的“误”解与正解。

1.“误”解（困惑） 用余弦定理直接求c

即c=3或5。

本题好像就可以结束了。实则不然。若c=3，则由余弦定理可以算得，此时B为钝角；实际上，，B=2A，由二倍角公式，-1=，这表明B为锐角，与前述矛盾。因此c=3其实为“增根”。经验证 满足条件，即为所求。

这里“增根”隐藏得很深，通常的矛盾如大边对大角（大角对大边）、负数根等情形都排除不了，的确难以发现。下面的正解可以回避讨论、检验“增根”，过程略显曲折。

2.正解

这里解题过程稍显“复杂”，但其中回避了讨论与验证，干净利落。

（三）更好选择，回归“初心”

例3 （2018年高考新课标全国Ⅰ卷）在平面四边形ABCD中，∠ADC=90°，∠A=45°，AB=2 ，BD=5。

（1）求cos∠ADB；

分析：本题是借用平面四边形为载体，初看条件，容易看成是平行四边形模型从而进入误区（一时半会儿作不出示意图，耽误时间、容易焦躁，影响心情、影响考试成绩）。解答本题必须先画出示意图（图1），本题是解三角形的常见题型。

图1

1.“误”解（困惑）

（1）问用余弦定理先求出AD，再用余弦定理求cos∠ADB，分析思路清晰、求解过程有条有理。

如图1所示，在△ABC中，∠A=45°，AB=2，BD=5。由余弦定理，，

再由余弦定理，在△ABC中，可算得

这里的计算量是惊人的。从②式到③式，在计算上都十分繁杂，一步错必将导致后续计算步步错。下面的正解将从正弦定理的角度来减少计算量，以便达到能够快捷解题的目的。

2.正解

（1）在ΔABC中，考虑正弦定理，

易见∠ADB为锐角，

（2）由题，∠ADC=90°，故。

在△BDC中，BD=5，，考虑余弦定理，

其实，本题还有更加简便的解法，可以不用所谓的正弦定理、余弦定理，直接口算。

3.另解：回归“初心”

如图2，过点B，作BE⊥AD， E为垂足；作BF⊥CD，F为垂足。易见四边形BEDF为矩形，△EAB为等腰直角三角形。

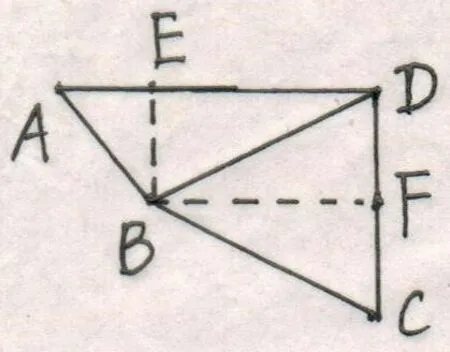
图2

（1）在Rt△EAB中，由勾股定理口算可得；在Rt△EBD中，由勾股定理口算可得。由余弦的定义，即有。

回归“初心”，“高等”数学“低等”化，不仅会给解题带来“眼前一亮”的“灵感”，而且会收获数学解题的快乐与满足。学习中的“小确幸”也是生活中的“大确幸”。

二、“结构不良”问题的求解探讨

（一）凭“直觉”做“恰当”选择

例4 （2021年高考北京卷）在△ABC中，内角A、B、C的对边分别为a、b、c，且c=2bcosB，。

（1）求B；

（2）在下列三个条件中选择一个作为已知，使 存在且唯一确定，并求BC边上的中线的长度。

①c=2b；

②△ABC的周长为；

③△ABC的面积为。

注意到是求角B，结合正弦定理运用“边化角”可得，代入数据即有，再由三角形内角和为π、，故B∈ ()。于是2B∈ (0,)，由正弦曲线立即可得，即。

这样细致的分析有助于后续问题的处理。这里分析得越清楚、透彻，三角形的大致形状也就会看得越清晰、简单，这些对数学解题是大有裨益的。

在（1）问的基础上求解（2）问。（2）问属于“结构不良”试题的典型问题，极具开放性，对数学逻辑推理的思维层次要求较高。下面主要探讨求解（2）问的困惑与应对策略。

1.“误”解（困惑） 选择条件①：c=2b

从另一个角度看条件①：c=2b，结合正弦定理知，这表明，与题目条件矛盾。故这样的△ABC不存在。

考试中的选择须要快速、精准，不能在条件①上耗费时间和精力，要能够迅速找到△ABC不存在的理由。其实在前面的解答中（包括题干条件）找不到关于长度、面积等“长度”的度量，而条件①：c=2b其实是“边”之间的比例关系，如何能求出BC边上的中线的长度？试想：满足题目条件的三角形即便存在，由三角形相似可知其也必不唯一，而是有无穷多个，也不合题意。

取BC边上的中点D。

在△ABC中，结合，由余弦定理可以直接得出BC边上的中线的长度为。

由a=b、，面积为，于是=，故b=4。从而a=b=4，c=。

类似于上述解答过程，可得BC边上的中线的长度为。

很明显，选择条件②、条件③都能使△ABC存在且唯一确定，而且这两种情况下的运算量也差不多，都是所谓的“通法通解”的范畴，是学习中应该掌握的精熟的常规解题办法。

对于条件③：△ABC的面积为，为了求出三边之长，面积公式的选择其实是多种多样的。除了上述常规方法外，还可以选择（Heron（海伦）公式，其中、（秦九韶“三斜求积”公式）等，但它们都没有用常规方法解题来得简洁、快速、高效。

（二）凭“存在”做“合理”推论

例5 （2021年高考新高考Ⅱ卷）在△ABC中，内角A、B、C的对边分别为a、b、c。若b=a+1，c=a+2。

（1）若2sinC=3sinA，求△ABC的面积；

（2）是否存在正整数a，使得ΔABC为钝角三角形？若存在，求a；若不存在，请说明理由。

分析：本题（1）问用正弦定理“角化边”立即可得2c=3a，再由题目条件b=a+1，c=a+2，故a=4、b=5、c=6。

注意到角是锐角，先用余弦定理求出

再由同角关系得到

因此△ABC的面积为。

本题（2）问“误”解（困惑）点主要是对存在性问题的基本处理方法。一般都是先假设“存在”，加上原题干的条件，再在此基础上进行合理的逻辑推导，若能顺势求出“存在”那自然就存在了；倘若推出“矛盾”的结果（例如，例4中（2）问中的条件①）那当然先假设的“存在”就不存在了。这种对逻辑推理素养的培养至关重要，其在学习生活中处处有用。

现在回到本题（2）问上来，先假设存在正整数a，使得△ABC为钝角三角形，试着求出a。

事实上，欲构成三角形，必须两“边”之和大于第三“边”，注意到c最大，故只需a+b＞c ，解出a＞1 。

同时欲使△ABC为钝角三角形，则角C必为钝角。由余弦定理、结合三角函数的性质知，只需cosC＜0 ，故，又a＞0，解出1＜a＜3，从而a=2。经验证，合题。

即存在a=2 ，使得△ABC为钝角三角形。

三、教学启示

横看成岭侧成峰，远近高低各不同。学会从问题的不同侧面去处理问题，在对比中学会取舍、感悟、提升，带着疑问去理解问题、分析问题，真正把解三角形的各种情形进行归纳、总结，要对题目条件、待解决的问题等同时进行化简、抽丝剥茧，直抵问题的内核。只有经过如此训练方可举一反三、熟能生巧。

数学学科核心素养的落地生根离不开对数学问题深入细致的探究。数学运算与逻辑推理相辅相成、相得益彰，借助于直观想象可对数学抽象进行感知、理解，进而用数学思想来解决生产生活中的实际应用问题、发挥好数学应有的工具性作用。