基于修正协方差近似二阶扩展卡尔曼滤波算法的电池荷电状态估算*

王伯运 何耀 郑昕昕

（合肥工业大学，合肥 230009）

1 前言

目前，锂离子电池荷电状态（State Of Charge，SOC）估计方法主要有安时积分法[1]、卡尔曼滤波系列算法[2]、开路电压法[3]、基于数据驱动的方法[3]等。安时积分法根据电流对时间的积分进行计算，再根据初始SOC 进行SOC 的实时计算。但该方法难以获取精确的SOC 初值，无法满足车辆行驶过程中的实时性要求。开路电压法的理论依据是电池在长时间静置的条件下，开路电压（Open Circuit Voltage，OCV）与SOC存在相对固定的函数关系[4]。精确的开路电压获取条件苛刻，该方法无法满足车辆行驶过程中的实时性要求。卡尔曼滤波法能给出SOC的估计值及估计误差，同时具有收敛快、估算精度高、对SOC初值不敏感等优点，因而得到广泛应用[5]。

目前，已有众多学者利用卡尔曼滤波及其衍生算法估算电池SOC。崔耕韬[6]等使用扩展卡尔曼滤波（Extended Kalman Filter，EKF）算法估计锂电池SOC，在恒流放电工况下电池的SOC 估计误差约为2.1%。周斌[7]等在二阶RC 等效电路模型下利用模糊控制联合扩展卡尔曼滤波、安时积分和开路电压等算法建立电池SOC 的联合估算模型进行估算。李岩[8]等在传统的无迹卡尔曼滤波（Unscented Kalman Filter，UKF）算法基础上加入球型选点规则，提升了算法的估算精度。胡波[9]等基于等效电路模型的递推最小二乘法（Recursive Least Square，RLS）结合容积卡尔曼滤波（Cubature Kalman Filter，CKF）的方法提升了算法的估算精度。

相比于UKF 和CKF 算法，EKF 算法利用提前计算雅可比矩阵的方式实现以较低的计算压力对非线性系统进行观测。EKF 算法在泰勒公式展开实现线性化的过程中将高阶项省略，算法本身有一定缺陷，且由于测量噪声不可控，对误差敏感[10]。在算法迭代过程中协方差易出现病态，导致SOC 估计出现较大误差。

修正协方差近似二阶扩展卡尔曼滤波（Modified Covariance Approximate Second-Order Extended Kalman Filter，MVASOEKF）算法在EKF 算法的基础上，采用应用均值变换的二阶近似、方差和协方差变换一阶近似[11]的方式来尽可能减小因省略高阶项引入的误差，且在计算过程中不断更新计算雅可比矩阵，使协方差在更新迭代过程中渐渐收敛，减少了协方差病态问题的出现。因此，本文建立二阶RC等效电池模型，将实测端电压数据与等效模型数据进行对比，验证电池模型精度，选用MVASOEKF 算法，在MATLAB/Simulink 平台上进行SOC 估算，将SOC 的实测值与MVASOEKF 和EKF 算法的估计值进行对比。

2 锂离子电池模型

在等效电路模型[12]中，电池被视为由电阻、电容等简单的电气元件组成的电路模型，该模型能够很好地反映电池的外部特性，比较符合电池实际工作过程中的表现。常见的等效电路模型有戴维南（Thevenin）模型[13]、RC 模型[14]、新一代汽车合作伙伴计划（The Partnership for a New Generation of Vehicles，PNGV）模型[15]和Rint 模型[16]。模型的选取要考虑模型的精度和复杂度等因素的影响，从精度、复杂度和鲁棒性等多个维度对11 种等效电路模型比较的结果表明，二阶RC模型是较理想的选择[17]。

二阶RC等效电池模型如图1所示，其中R0为欧姆内阻，R1为电池浓差极化电阻，C1为电池浓差极化电容，U1为极化电压，R2为电池电化学极化电阻，C2为电池电化学极化电容，U2为极化电压，UL为端电压，Uoc为开路电压，I为回路电流。

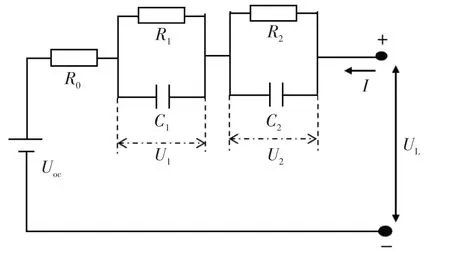
图1 二阶RC电池模型

由基尔霍夫电流定律可知：

由基尔霍夫电压定律可知：

式中，Ssoc为电池荷电状态。

3 电池模型参数识别

3.1 混合脉冲功率特性试验

在二阶RC 模型中需要精确识别出SOC 与R0、R1、C1、R2、C2等内部参数的关系。目前，混合动力脉冲功率特性（Hybrid Pulse Power Characteristic，HPPC）因测量方便快捷而被广泛使用[18-19]。本文根据美国《FreedomCAR 电池测试手册》[20]中的规定进行混合脉冲功率特性试验对电池参数进行辨识。试验采用1 C 的脉冲充放电电流，先放电10 s，之后静置40 s，再充电10 s，最后静置。使用的Panasonic-18650 锂离子电池参数如表1 所示，通过分析试验得到的电压波形图辨识出电池内部参数。图2所示为Ssoc=0.5时HPPC脉冲电流与电压变化曲线。

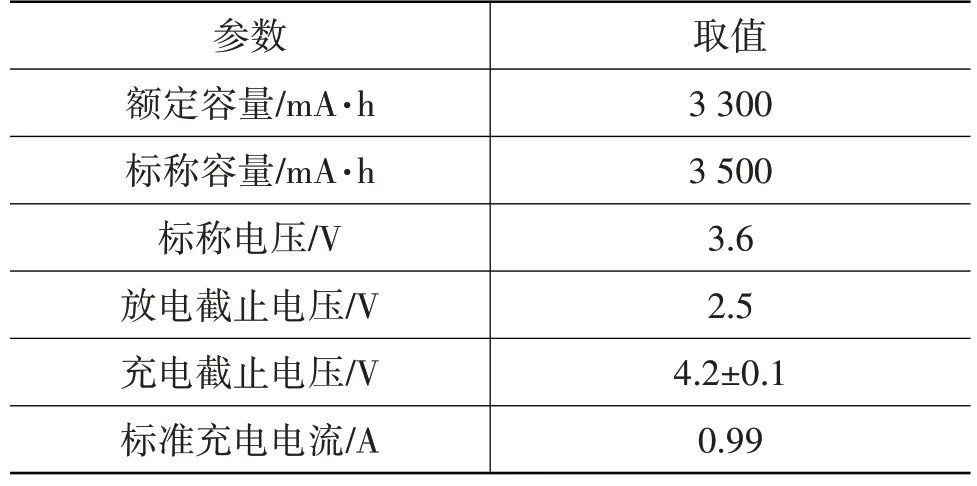
表1 Panasonic-18650电池参数

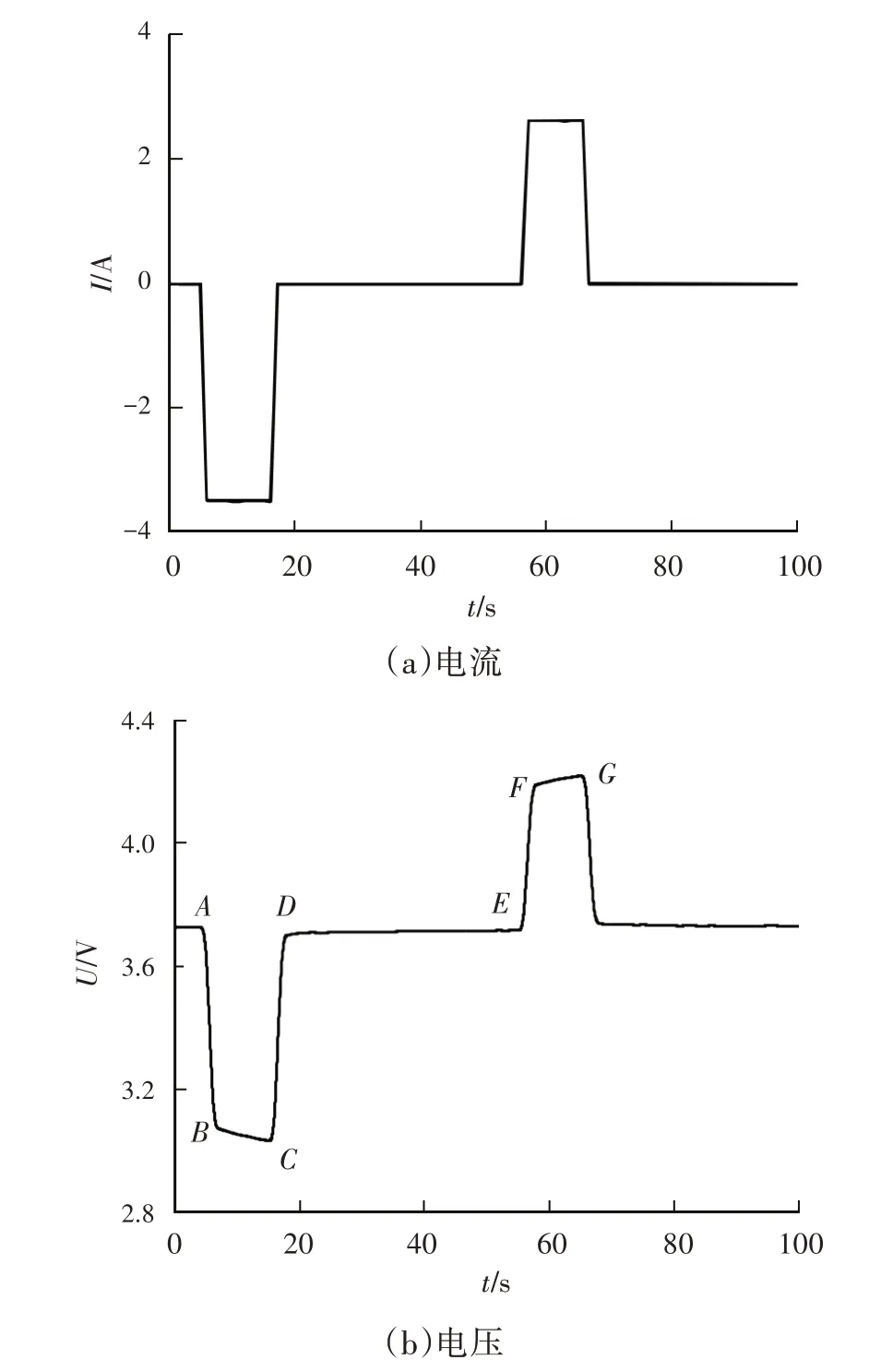
图2 HPPC脉冲电流与电压变化曲线

3.2 模型参数识别

3.2.1 SOC与开路电压的关系

在每次试验放电结束后将电池静置2 h，静置后的电压可视为电池的开路电压，记录每次脉冲放电试验后的SOC与其对应的开路电压，如表2所示，再利用MATLAB 拟合工具拟合出二者的关系曲线如图3所示，其关系式为：

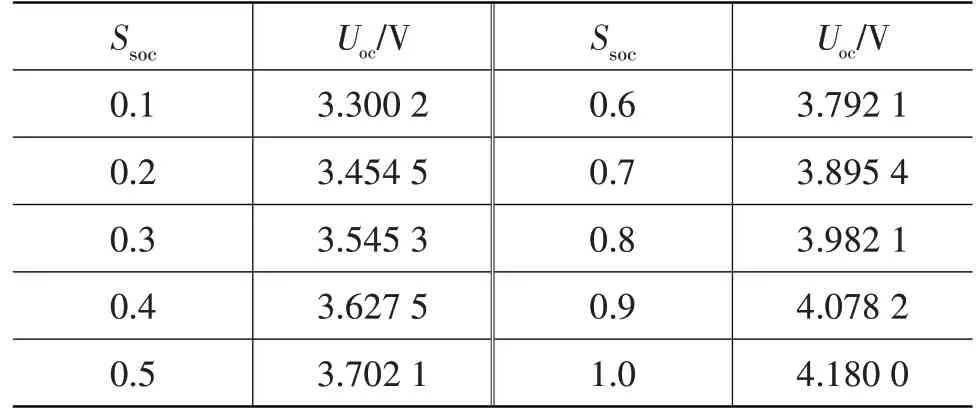
表2 SOC与OCV的关系

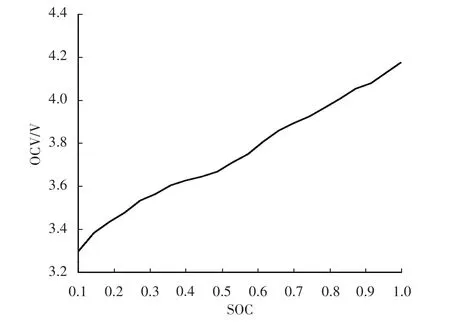
图3 OCV-SOC拟合曲线

3.2.2 内阻R0辨识

在充放电开始和停止瞬间，锂电池端电压会发生突变，是由欧姆内阻R0造成的。可以选取两电压差的均值与电流的比值作为内阻R0：

式中，UA、UB、UC、UD分别为图2b 中A、B、C、D点的电压。

3.2.3 极化电容与极化电阻辨识

在图2 中B点到C点所在时刻之间，锂电池端电压从UB平滑过渡到UC，这是由2 个RC 电路造成的，在此时间段极化电容存在缓慢充电的过程，极化电容两端的电压呈现指数增长，从而导致端电压出现明显下降。

从D点到E点所在时刻电池处于静置状态，此阶段下的二阶RC 电路可以视为零输入响应。对电路进行时域分析，可以得到端电压UL与时间t的函数关系：

式中，τ1=R1C1、τ2=R2C2分别为2 个RC 电路中的时间常数。

将D点到E点所在时刻期间的回弹电压与时间t的关系曲线通过MATLAB 中的拟合工具箱中的自定义二阶指数函数拟合，拟合结果为：

式中，H、G、K、h、g为拟合曲线的待定系数。

将式（5）与式（6）联立相等可以得到电池模型内部参数：

由此，利用上述辨识方法，可以确定电池模型在不同SOC点处的内部参数，如表3所示。

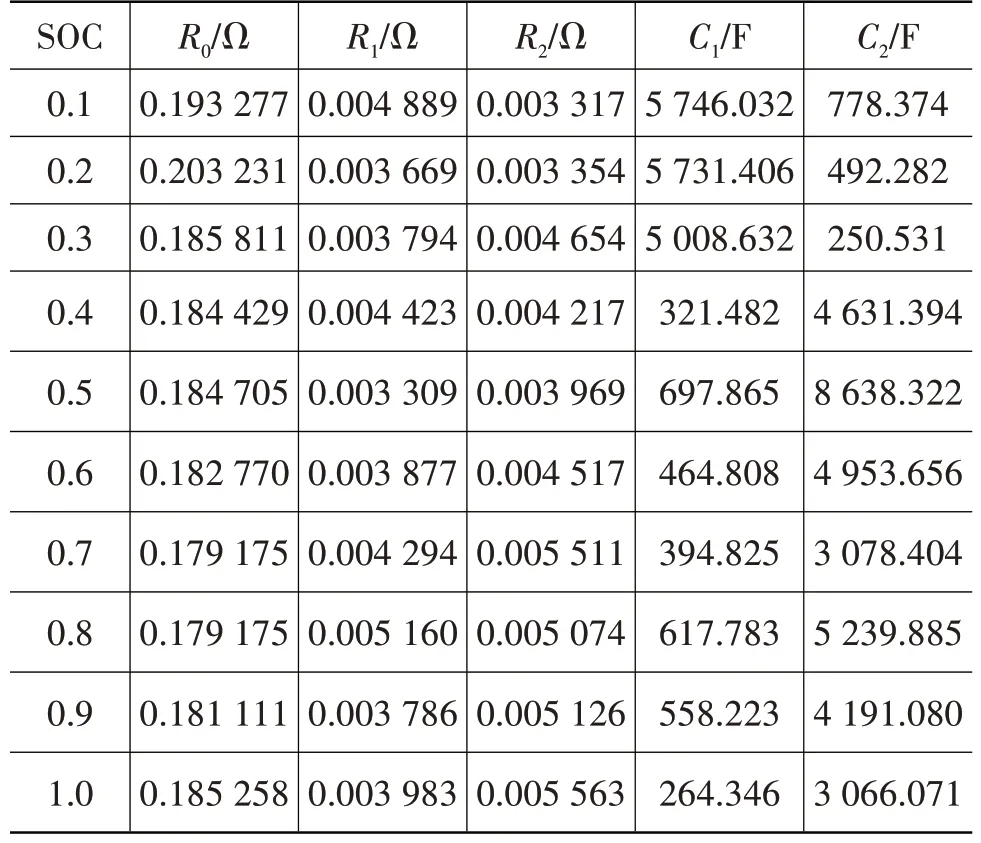
表3 不同SOC点处电池内部参数

4 MVASOEKF算法

非线性离散系统由状态方程和观测方程组成，系统公式分别为：

式中，xk为k时刻的状态量；uk为系统k时刻的输入量；yk为k时刻的系统观测量；wk-1、vk分别为(k-1)时刻均值为0 的过程噪声和k时刻均值为0 的测量噪声，且两者互不相关：

式中，Qk、Rk分别为k时刻过程噪声的协方差矩阵和测量噪声的协方差矩阵；E[X]为随机变数X的期望值。

在每一个时刻，利用一阶泰勒展开法将f(xk-1,uk-1)和g(xk,uk)线性化：

结合式（11）、式（12）、式（14）、式（15），可以得到非线性系统线性化后的表达式：

MVASOEKF算法的具体流程如下：

a.初始化阶段

式中，为0 时刻的状态变量修正值初值；P0|0为0时刻预测误差协方差矩阵初值；x0为0 时刻的状态量初值；Var(x0)为变量x0的方差。

b.预测阶段

计算状态方程雅可比矩阵Ak为：

状态变量预测值|k-1为：

状态变量预测值误差协方差矩阵Pk|k-1为：

式中，Pk|k-1为(k-1)时刻的状态变量修正误差协方差矩阵。

c.状态更新修正阶段

观测方程雅可比矩阵为：

卡尔曼滤波增益矩阵为：

状态变量值为：

d.二次状态修正更新阶段

重新计算观测方程的雅可比矩阵Ck为：

重新计算卡尔曼滤波增益矩阵Kk为：

状态变量修正误差协方差矩阵Pk|k为：

式中，E为单位矩阵。

状态变量修正值|k为：

MVASOEKF 算法以电池的SOC、电容C1、C2两端的电压U1、U2作为系统的状态变量，以电流I作为输入量、电池端电压UL作为观测量，根据式（1）、式（2）和安时积分表达式建立电池模型状态空间方程：

式中，Cn为电池额定容量。

电池观测方程为：

将式（28）、式（29）进行离散化处理后的状态方程为：

式中，Ts为采样周期；I(k)为k时刻的电流。

输出方程为：

综合式（30）、式（31）可得空间方程为：

记MVASOEKF算法相关矩阵为：

式中，Xk为状态变量矩阵；Bk为输入矩阵。

5 验证试验与结果

5.1 验证试验

依据MVASOEKF 原理以及电池辨识的参数，建立等效电池模型和SOC 估算模型。将实测的端电压数据与等效模型数据进行对比以验证电池模型精度；将实测的SOC 值与采用MVASOEKF 和EKF算法的SOC 估计结果进行对比，检验模型的精确度。本文使用Panasonic-18650锂离子电池，电池参数性能见表1。

5.2 试验结果

5.2.1 电池模型精度验证

本文采用北京公交动态测试（Beijing Bus Dynamic Stress Test，BBDST）工况对模型进行精度测试，该工况是对北京公交车起步、加速、滑行、制动、急加速、停车等各环节中的电池组数据采集后进行处理所得到的[21]。此工况数据为整个电池包的数据，本文的研究对象为锂离子电池单体，故需要根据实际情况对工况功率按比例缩小，BBDST工况试验数据如图4所示。

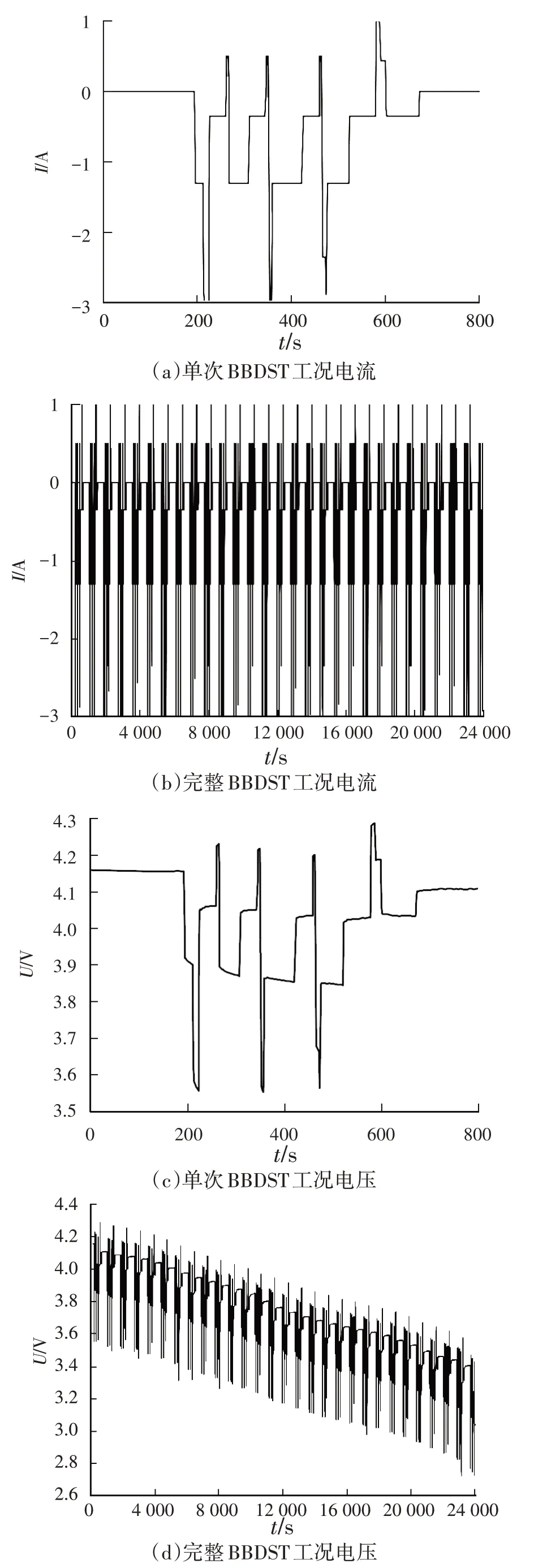
图4 BBDST工况数据

BBDST工况试验电池等效模型估计值及误差如图5所示，从图5中可以看出，二阶RC等效电池模型可以将绝对误差整体控制在50 mV以内，并且电池模型估计误差峰值只会出现在高电压和低电压时刻，即高SOC 和低SOC 状态。当SOC 在0～10%和90%～100%的范围内时，电池模型的估计输出电压会出现较大偏差，并出现估计误差的峰值，但是新能源汽车锂离子电池的实际工作范围一般为10%～90%，因此所建立的等效电池模型可以满足电动汽车的要求。

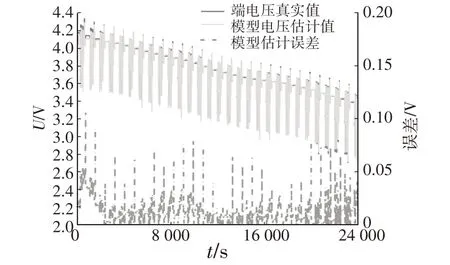
图5 电池等效模型估计值及误差

5.2.2 MVASOEKF算法验证

MVASOEFK 与EKF 算法初始参数设为P0|0=diag(0.04,0.04,0.04)，测量噪声协方差矩阵R0=[0.8]，过程噪声的协方差矩阵Q0=diag(10-4,10-4,10-4)。图6、图7 所示分别为电池SOC 初值为0.98 和0.70 时BBDST工况下的电池SOC估算结果。

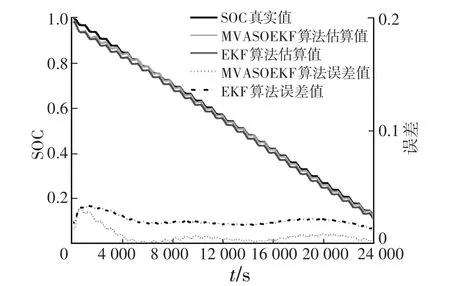
图6 初始SOC为0.98时的估算值及误差

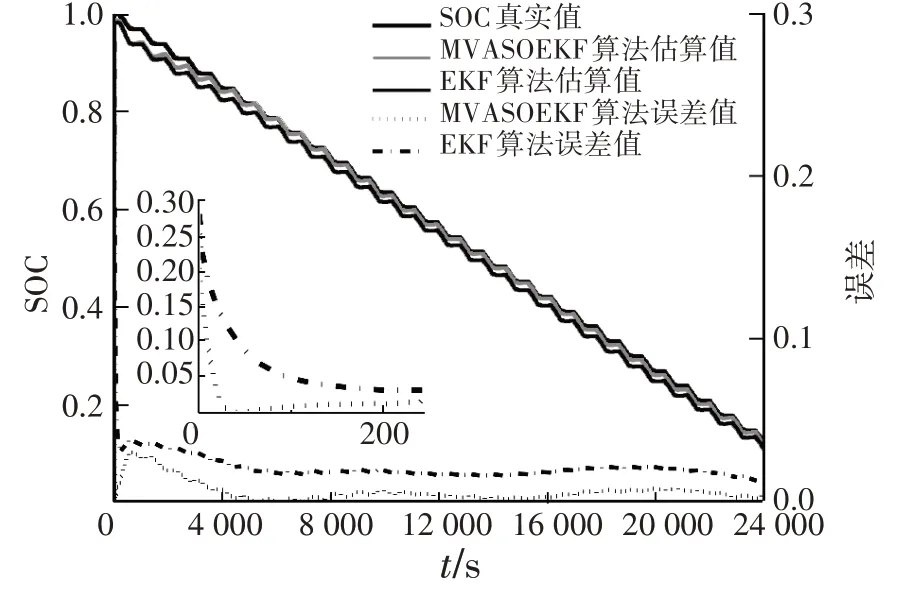
图7 初始SOC为0.70时的估算值及误差

由图6 可知，当SOC 的初值确定时（Ssoc=0.98），在RC 二阶电池模型下，MVASOEKF 与EKF 算法都能够与真实SOC 变换趋势一致，在第2 000 s 前SOC误差会出现峰值，这是由等效二阶电池模型在SOC为100%到90%之间时的估算误差引起的。

由图7可知，在SOC 的初值不确定的情况下，即算法初始设定值（Ssoc=0.7）与实际电池SOC 有明显差异时，以绝对误差值5%为标准，EKF、MVASOEKF算法都可以在一定时间内使SOC 估算值逼近真实值，MVASOEKF 算法约需20 s，EKF 算法约需200 s，这说明MVASOEKF 算法具有更强的收敛性。在解决初值误差和电池模型误差问题后，EKF 算法的平均绝对误差在2.0%左右，MVASOEKF 算法的平均绝对误差在0.5%左右。

为了更加清楚地评价2种SOC 估计算法的精度与可靠性，本文采用平均绝对误差（Mean Absolute Error，MAE）、平均相对误差（Mean Relative Error，MRE）、均方根误差（Root Mean Squared Error，RMSE）3种指标进行评价，结果如表4、表5所示。

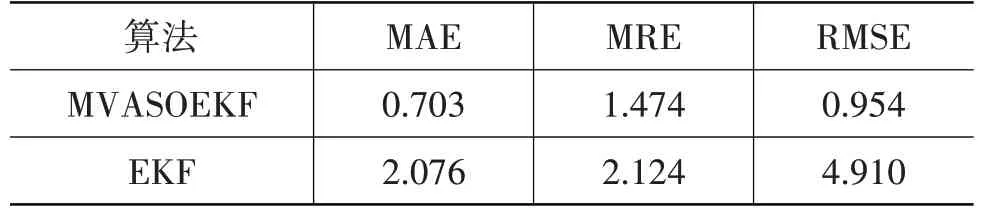
表4 初始SOC为0.98时不同算法下的估算精度 %

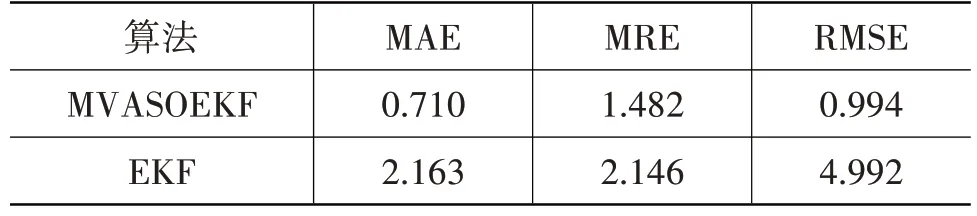
表5 初始SOC为0.70时不同算法下的估算精度 %

由表4、表5 可知，相比于EKF 算法，MVASOEKF 算法的MAE、MRE 和RMSE 值都更小，从统计学的角度来看，MVASOEKF 算法模型具有更高的精度和可靠性。

综上所述，MVASOEKF 算法具有更快的收敛性，更高的估算精度和更强的鲁棒性。

6 结束语

本文首先建立二阶RC 等效电路模型，并利用SOC的安时积分表达式和戴维南定理建立电池状态空间方程，最后通过MVASOEKF 算法估算电池的SOC。电池模型的参数通过MATLAB 中的拟合工具和混合脉冲功率特性试验结果进行离线对比拟合辨识，确保数据的可靠性。MVASOEKF 算法利用近似二阶的扩展卡尔曼滤波法减少因非线性变换中忽略高阶泰勒项而引入的SOC 估算误差，并且通过修正更新协方差的方式解决了在迭代过程中协方差易出现病态的问题。MVASOEKF 与EKF 算法相比，虽增加了一定的计算量，但是SOC 估计准确度有了明显改善，并且收敛性与鲁棒性更好。