项目式学习在小学数学“乘法分配律”教学中的应用
周淳凯
数学学科具有鲜明的工具性、综合性和实用性特点,对于培养学生的核心素养有着重要作用。项目式学习是一种以学生为中心的教学方法,它让学生通过参与一个具有实际意义和挑战性的项目,来探究和解决一个真实的问题或者完成一个复杂的任务。项目式学习不仅能提高学生的学习效率,让学生学到知识和技能,还能提高学生的创造力、合作能力、解决问题的能力,发展学生的批判性思维。在小学数学课程中,“乘法分配律”是乘法运算定律教学中的一个重点,在教授“乘法分配律”相关内容时,教师运用项目式学习方法,有利于发挥学生学习的主观能动性,培养学生的抽象思维。本文探讨了项目式学习在小学数学“乘法分配律”教学中的应用策略,以供参考。
一、立足素养,梳理实施思路
在小学数学教学中运用项目式教学法时,教师应着眼于具体问题,立足核心素养培养,梳理项目式教学的具体思路,制定适宜的教学目标。教师应将课堂主导权交给学生,为学生的自主学习搭建多样化结构空间,让深度学习自然发生。同时,教师要设计独立思考、动手实践、自主探索、合作交流等环节,引导学生进行自主探究。以小学数学“乘法分配律”的教学为例,教师可以结合《义务教育数学课程标准(2022年版)》的要求和学生的认知水平,制定以下教学目标。
第一,通过课堂理论知识的学习,学生能够理解乘法分配律的定义与内涵,了解乘法分配律的运用要素和使用规则,同时掌握乘法分配律的使用难点,对乘法分配律有初步的认知。第二,在训练学生运用乘法分配律时,教师要引导学生针对不同题型选择相应的方法,形成良好的计算思维。第三,教师要帮助学生在具体实践中联系生活实际,感知数学与现实生活之间的联系,从而使学生意识到数学在生活中的价值,提高學生运用数学知识解决实际问题的能力。
基于上述教学目标,教师要以学生的实际需求为切入点,开发、设计符合学生认知的数学探究项目,提高小学数学课堂教学效率。首先,教师应充分激活学生已经掌握的数学知识与实际经验。由于学生在学习乘法分配律之前已经具备基本的运算能力,教师可以从加减法运算导入,引出乘法分配律的概念。其次,教师要设计具体的项目任务,为学生创设探索空间,让学生进行观察、发现、猜想和验证,引导学生体会算式分别乘的特点。最后,教师要解决学生的认知冲突,为学生的实践探究指明方向。
二、数形结合,感悟数学本质
在小学数学项目式学习中,教师可以运用数形结合思想,将抽象的数学概念以具象化的图形呈现出来,帮助学生加深对相关概念的理解。以“乘法分配律”的教学为例,教师可以运用数形结合的教学方法,为学生讲解乘法分配律表达式,让学生感受“公有的因数”的结构特点,从而建立抽象的数学模型,并成功归纳出相关公式,掌握“分”与“配”的规律。
具体而言,教师在运用数形转化思维讲解“乘法分配律”时,可以利用瓷砖图和点位图辅助教学,帮助学生理解。比如,教师可以创设贴瓷砖的生活情境,利用多媒体设备向学生展示相关图片(图1),并提出相应问题:“小明家正在装修,请你算一算两面墙上一共贴了多少块瓷砖?”在具体情境的问题驱动下,学生能很快列出等式:4×9+6×9=(4+6)×9。

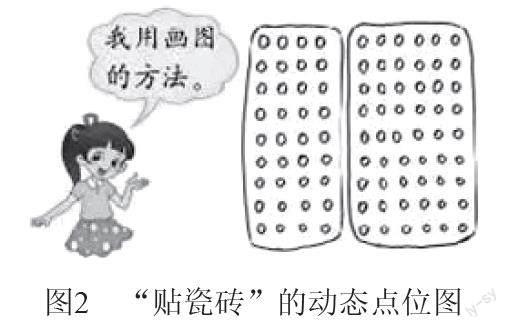
教师要引导学生发现该等式中的规律。比如,当有学生提出“等号两边算式不同但结果相同”的结论时,教师可以适时切入动态的点位图,以更加直观的形式向学生展示数与形之间的规律(图2),并鼓励学生根据点位图展开讨论。在教师的逐步引导下,当学生横向观察图2时会发现,每一行的瓷砖是4块加6块,一共有9行,由此得出(4+6)×9等于9个(4+6)的结论,等式两边结果相等;当学生竖向观察图2时会发现,每一列有9块瓷砖,一共有4列加6列,由此得出(4+6)×9等于10个9相加的结论,且等式两边的结果相等。由此可见,在项目式教学中,教师借助具象图形,可以让学生清楚地认识“乘法分配律”的算法逻辑。
三、变式辨析,促进融会贯通
在实际问题中,乘法分配律的算式不全是(a+b)×c或a×c+b×c的标准结构形式,其多样的形态结构会让学生感到困惑,学生很难快速抓住解题要素。从某种程度上来说,算式变化是训练学生思维的关键,教师一味采用同质化试题引导学生反复练习是不可行的,应引导学生在多样变式中认识算式的本质。对于不同形态结构的算式,教师要引导学生找到其与标准结构形式之间的联系,将变式转化为标准结构,这是解决复杂问题的关键。因此,在教学“乘法分配律”时,教师要指引学生在不同变式中不断转换观察角度和思路,通过比较、分析来化难为易。笔者以如下两类变式为例进行探讨。
第一,在分析“变式一:103×28”时,教师首先要引导学生仔细观察,分析算式更接近于哪一种标准结构,然后思考能否对它进行有效转化,最后让学生解答。学生在分析、比对后发现,算式要求计算103个28是多少,那么就可以将103视作1个100和1个3,分别计算100个28和3个28的结果,这更接近于(a+b)×c的分配律形式,即103×28=(100+3)×28,并进一步得出结论:在计算接近整百的算式时,可以先将其解构为整百数加(减)另一个数的形式,再转化成标准的乘法分配律结构,从而化繁为简,快速解答。
第二,“变式二:99×52+
52、101×48-48”这类题型是学生比较容易出错的题型,属于“积加(减)一个数”的范畴。教师在对学生进行指导时,常态化的方式是从意义层面进行剖析,99×52+52就是99个52加上1个52,转化为100个52,即99×52+52=(99+1)×52,101×48-48同理。但在计算的过程中,由于这种外在结构具有一定的隐秘性,学生很容易出现判断失误的情况,尤其是在加减混合观察的过程中,部分学生仅靠逻辑分析很难代入已掌握的公式结构。基于此,教师应着重指导学生掌握这类变式的转化过程,要引导学生判断该类题型与哪种标准结构相近,并使用相近的“a×c+b×c”法则得出99×52+1×52或101×48-1×48的标准结构形式,从而简化思维过程,减少计算失误。
数学学科的教授不仅仅强调知识的有效传递,更强调对学生思维的启发与培养。即使是简单的计算问题,教师也要引导学生掌握正确的思维方法,让学生通过观察、分析、转化,明确解题思路,构建数学模型,为学生将来的数学学习奠定思维基础。
四、锻炼思维,敏锐洞察规律
学生对“乘法分配律”的敏锐性主要体现在,对于一些容易混淆的题型能够灵活使用定律进行简便运算。在这一过程中,学生的简便运算能力和敏锐性是关键。因此,在项目式教学后期,教师应有意识地培养学生对算式和算法内在规律的洞悉能力,在解决问题的过程中发展学生的高阶思维。为了锻炼学生的思维能力,培养学生对“乘法分配律”的敏锐观察力,教师可以从以下两个方面做起。
一方面,数学语言具有简洁性和概括性的特点,教师在教学中要指导学生掌握和了解数学语言的规律,这有利于学生高效审题,快速找出题干中显性和隐性的条件,进而从浅层次的知识学习进入深层次的学科素养提升。另一方面,在项目式教学模式下,教师要帮助学生提炼算式背后的结构性知识,让学生运用形式化、可视化的数学符号,准确地表达出相应的数学结构,构建乘法分配律的符号模型,提高学生获取和概括知识的能力。
在具体实施过程中,教师可以适当引进不同题型的练习题,有针对性地锻炼学生的敏锐度。比如,教师可以设计以下练习。一是巧填数,巩固模型,如:(51+49)×6=□×6+□×6;65×5+35×5=(□+□)×□。二是巧计算,应用模型,如:(132+8)×8;201×6-6;61×201。
三是巧列举,寻找模型,如:请你自行列举几个关于乘法分配律的模型。四是巧编题,理解模型,如:根据所学的知识,请你尝试编一道关于乘法分配律的题目。这些不同题型的设计背后蕴含了分层、分级、多样化的训练思路,有助于发展学生的求异思维、发散思维和逆向思维,帮助学生构建相应模型来解决问题,从而有效锻炼学生的数学敏锐性,提高学生的应用能力。
五、抽丝剥茧,完善知识体系框架
数学知识体系的构建是一个螺旋式上升、循序漸进的过程。在小学数学项目式教学视域下,教师要循序渐进引导学生探究数学知识的本原,通过数学思维与核心素养的拓展教学,帮助学生贯穿前后知识点,让深度学习自然发生。
第一,在项目式教学伊始,教师应深入解读《义务教育数学课程标准(2022年版)》、教材编排制订意图,领会新时期数学教学的丰富内涵,紧扣知识点为学生创设问题情境,唤醒学生旧知,激活学生的探索经验,帮助学生梳理知识点间的内在逻辑,促进学生积极投入课堂教与学的全过程,进行新旧知识的有效迁移。
第二,教师要基于数学知识体系的层次性特征,把握好课程内容的重难点,将分散的知识点串联起来,以全局观连点成线、连线成面,帮助学生构建完整的知识体系框架。教师要让学生在解决问题的过程中,通过体会不同的解决方法,进一步掌握“乘法分配律”,继而构建运算规律模型。
第三,教师要以“学会”为目的,指导学生自己得出“乘法分配律”,并为学生提供不同变式,给学生留下思考空间,促使学生展开深度学习。在课堂回顾和总结环节,教师要引导学生从乘法意义的角度去理解“乘法分配律”,使其掌握乘法分配律的本质,进而帮助学生提升数学核心素养,形成完整的知识体系框架。
(作者单位:苏州市吴中区姑苏实验小学)

