基于混合迭代贪婪算法的分布式车间调度研究

杜松霖,仵大奎,时宗胜,陈 曦,周文举

(1.上海大学机电工程与自动化学院，上海 200444；2.江苏中天互联科技有限公司，江苏 南通 204550； 3.新疆金风科技股份有限公司，新疆 乌鲁木齐 830026)

0 引言

调度问题广泛地存在于实际加工制造的流程控制过程中，如仪器仪表、线缆、风力发电机等产品的设计、生产、物流、管理等环节。调度方法及策略的研究一直是智能制造系统增效、节能、减排、降耗的核心与关键[1]。同时，随着经济全球化与生产国际化进程的加快，分布式协同制造模式也逐渐成为国际智能制造的主要方式之一[2-3]。分布式协同生产过程需要考虑多条分布式生产线及各条生产线内部的协同制造。因此，相较于传统单一流水线的生产模式，工件以及机器分配、工件排序造成的大规模、强耦合性是难以实现高效全局优化的难点与痛点之一[4]。

当前以不同约束条件下分布式协同制造系统各生产线之间工件的分配、生产线内部的机器指派以及工件排序等痛点问题为驱动，借助不同智能优化算法实现多个耦合子问题的解耦，确保生产调度方案的高度可行，以实现各种决策量的协同优化与全局优化。这有效解决了许多分布式生产调度问题，如分布式置换流水车间调度[5]、分布式零空闲流水车间调度[6]、分布式零等待流水车间调度[7]和分布式阻塞流水车间调度[8]等。

本文以总装配时间为优化目标，提出一种混合迭代贪婪(hybrid iterative greedy,HIG)算法，以求解分布式装配阻塞流水车间调度问题(distributed assembly blocking flow-shop scheduling problem,DABFSP)。

1 DABFSP研究现状

以分布式协同生产为背景，越来越多的制造企业不再是单纯地生产最终交付产品，而是同时具备生产定制产品或相应零件的能力。由供应链上游企业生产的零部件被转移到组装流水线进行统一组装，待所有的部件组装完成后对最终产品进行储存或市场投放。这一模式催生出分布式装配生产。属于同一产品的不同零部件在不同工厂的流水线上分别加工。各加工工厂能够更加充分地利用自身优势，选择更加科学、绿色、合理、高效的方式进行生产。各加工流水线之间的协同生产，以及组装流水线与加工流水线之间的协作运营，使得上述各类相关企业在降低生产成本的前提下，能够科学规避企业生产、运营风险，从而满足其长远发展的战略目标。这也使得协调生产更加适应经济全球化、生产国际化、制造智能化绿色化的大环境。因此，基于多个协同生产中心的分布式装配调度问题受到业界越来越多的关注。

分布式装配阻塞流水车间生产过程可分为协同加工过程和统一装配过程[9]。

协同加工过程主要负责产品零部件的生产或加工。该过程在分布式协同加工工厂内部完成。同时，协同加工过程遵循具有阻塞约束的流程式加工工艺。因此，该加工过程涉及零部件的分配，以及在每条流水线上零部件的生产调度，需要解决的关键性问题带有非线性与强约束性。至今，有不少研究学者提出了各类求解算法试图有效解决此类问题，如分散搜索算法[5]、迭代参考贪婪算法[10]等。

统一装配过程则主要负责将各种生产完成的产品零部件组装成最终可以流向市场的待售产品。该过程在单一组装流水线上完成。统一装配过程同样满足流程式组装工艺，同时又与前一阶段的分布式协同生产过程密不可分、互相制约，与分布式调度问题相比更具挑战性。

2 DABFSP描述

分布式装配阻塞流水车间调度过程如图1所示。

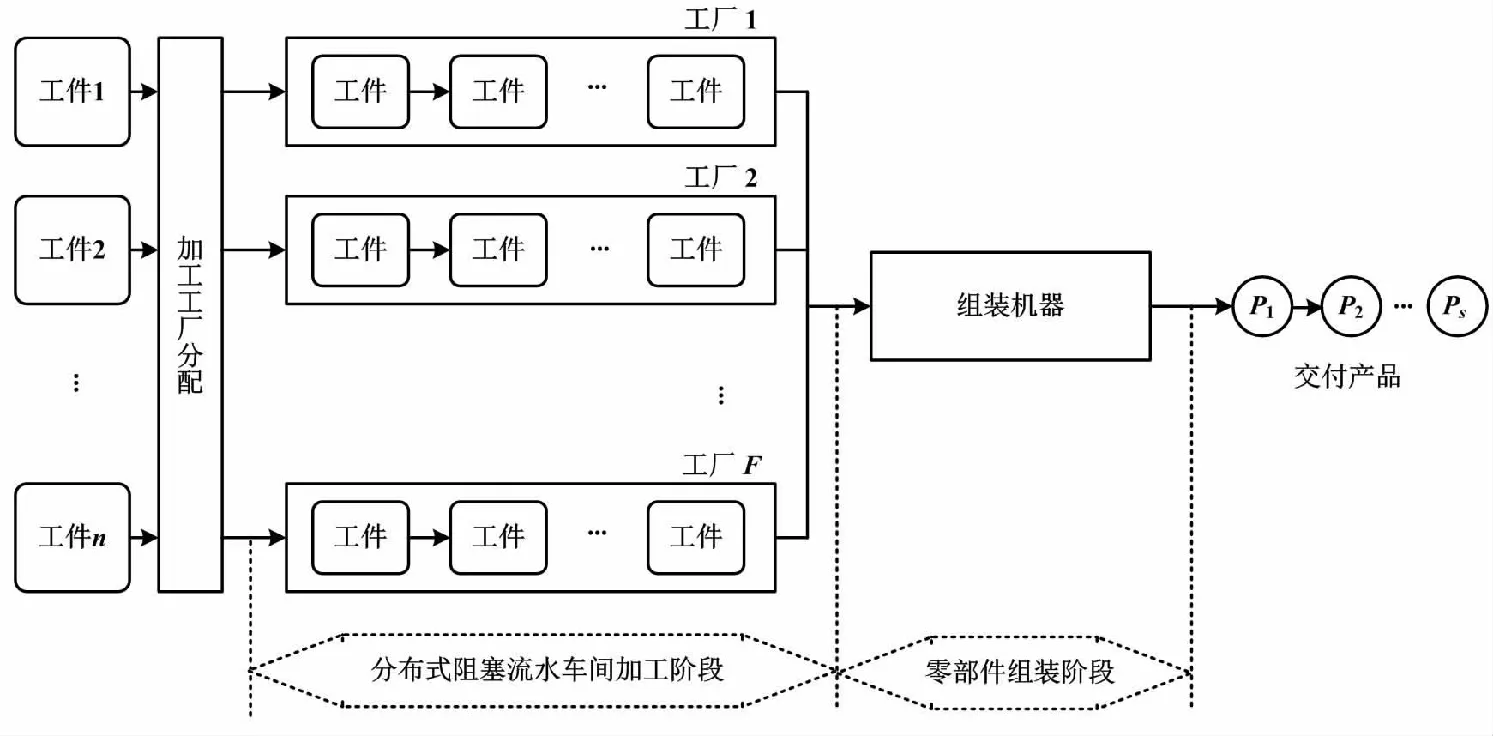
图1 分布式装配阻塞流水车间调度过程示意图Fig.1 Distributed assembly blocking flow-shop scheduling process diagram

DABFSP包括1个带有阻塞约束的分布式协同加工过程及1个单机的流程式组装过程。

DABFSP的优化目标Cmax(π)的计算过程如下。

①计算所有工件的加工完成时间。

②根据组成每个产品最后完工零件的结束时间,确定各产品的最早开始组装时间。

③根据组装流程工艺约束,计算所有产品最终的装配完成时间。

表1列举了1个DABFSP实例。

表1 DABFSP实例

表1实例包含8个待加工工件、5台机器、4个加工工厂和4件产品。假设调度顺序为π1=[6,5]、π2=[7,1]、π3=[4,3]、π4=[8,2]。

①由加工序列和每个产品的加工时间,可得每个工件的加工完成时间。

步骤①的计算结果如表2所示。

表2 步骤①的计算结果

②由表2可知:组成产品P1的最后一个加工完成的工件是工件J5;组成产品P2的最后一个加工完成的工件是工件J1;组成产品P3的最后一个加工完成的工件是工件J3;组成产品P4的最后一个加工完成的工件是工件J2。因此，组成产品P4的所有工件率先进入装配过程，其开始时间为254 ms，然后依次是产品P2、P1、P3。

③由于产品P4的开始组装时间为289 ms、装配时间为48 ms，因此装配完成时间为289+48=337 ms。此时，组成产品P2的所有工件均已加工完毕(即337>293)，则产品P2的开始组装时间为377 ms，装配时间为187 ms，装配完成时间为337+187=524 ms。以此类推，经计算可得按照加工序列π1=[6,5]、π2=[7,1]、π3=[4,3]、π4=[8,2]进行产品的加工和装配时的最大装配完成时间为289+48+187+183+190=897 ms。

3 迭代贪婪算法

迭代贪婪(iterated greedy,IG)算法最初是为了解决置换流水车间调度问题而产生的经典算法。其主要步骤包括初始化、破坏-重构、局部搜索以及接收准则。DABFSP是一类典型的离散问题，求解的时候不能直接使用解决连续问题的优化方法。因此,本研究提出的HIG算法中包含的各种机制均是在基于工件序列编码的基础上，充分融合DABFSP的问题特征实现的。

3.1 初始化

初始化第一步是根据待加工工件的总处理时间，对属于同一产品的各个工件进行降序排列。因此，优先加工的是总处理时间较大的工件。重复该过程，直到考虑所有待加工工件为止。结合表1中的实例，算法初始化第一步计算结果如表3所示。

表3 初始化第一步计算结果

初始化第二步是以第一步产生的工件序列为输入，逐个将每个产品的所有工件在分布式协同加工工厂中分别加工，计算工件在所有可能的邻域位置中的加工完成时间并选择加工完成时间最小的位置插入。待组成此产品的所有工件均插入最优的邻域位置后，可确定此产品的工件加工初始序列。重复上述过程，直到考虑所有产品。算法初始化第二步计算结果如表4所示。

表4 初始化第二步计算结果

由以上步骤可得初始化加工序列为{4,3,6,5,7,1,8,2}。初始化第一步的主要目的是确定属于每个产品的所有工件加工的顺序。该顺序是以工件为单位，在产品内部进行排序。初始化第二步的主要目的则是确定整个分布式协同加工阶段加工产品的顺序，是以产品为单位，在整个序列中进行排序。由上述2个步骤可以初步得出整个分布式协同加工阶段所执行的可行调度序列。

3.2 破坏-重构

在初始化序列中，由于所得初始解是结合问题特征由特定排序方式，即启发式方法产生的构造解，故排序方式直接影响着该解的质量。为了使算法在面临不同问题时依然能够有效求解，本研究在破坏和重构过程中考虑使用基于工件的交换和插入操作，通过破坏初始序列的结构以产生更高质量的新的重构序列，从而使算法适应不同类型的问题。

基于工件的交换和插入破坏-重构如图2所示。图2中，深色方块表示当前被操作的工件。由图2可知，HIG算法在初始化操作完成以后，对初始解随机选择交换或者插入操作进行破坏-重构，并以此提高算法求解问题时的稳定性。HIG算法是基于单解的优化算法。因此在执行此操作时，HIG算法对初始化产生的序列中的1个随机的工件，进行随机的交换或插入。

图2 基于工件的交换和插入破坏-重构示意图Fig.2 Schematic diagram of artifact-based swap and insertion destruction-reconstruction

3.3 局部搜索

根据破坏-重构操作产生的候选序列，将序列中的工件逐一插入分布式协同加工工厂中每个可能的位置，并选取最小装配完成时间的位置作为此工件的最终位置。重复上述步骤，直到考虑所有的工件。局部搜索操作如图3所示。

图3 局部搜索操作Fig.3 Local search operations

图3中，深色方块表示当前被插入的工件。

HIG算法在执行局部搜索操作时，由破坏-重构的序列考虑所有可能的邻域位置，并选择优化目标最小的邻域位置进行插入。此过程不仅能有效降低算法的复杂程度，而且能够快速逼近邻域最优解，提升了算法精确度。同时，本研究使用以下接收准则确保解的多样性。

①当经过局部搜索操作产生的序列比上一次迭代产生的最优解序列更优，则此代可行解直接保留并进入下一次迭代。

②当经过局部搜索操作产生的序列比上一次迭代产生的最优序列差，但是比历史最差解要好，则此代可行解也进入下一次迭代，但不保留。

3.4 算法流程

本研究提出的HIG的伪代码如下所示。

①开始。

②使用初始化方法构造初始化调度序列。

③t=1。

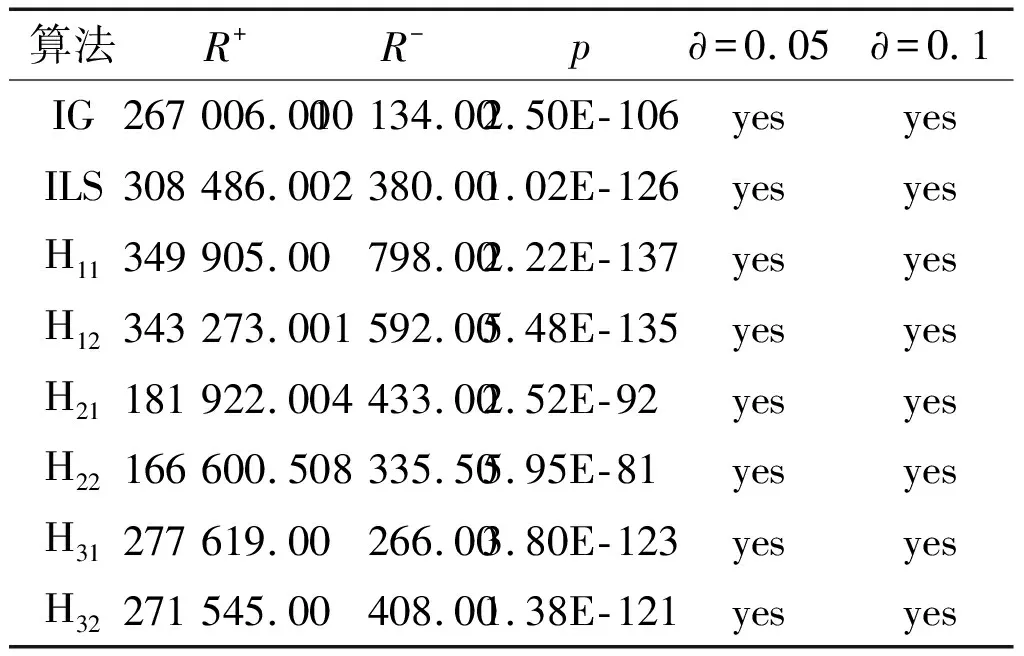
④while (t

⑤使用破坏-重构方法更新可行解。

⑥使用局部搜索方法更新可行解。

⑦计算可行解的适应度值，依据接收准则选取进入下一代的可行解。

⑧t=t+1。

⑨end while。

⑩输出最优解。

4 试验设置及结果分析

4.1 试验设置

为了分析所提出的HIG算法的性能，本文选择在900个问题实例上进行试验验证。这些问题实例由不同的待加工工件数量、机器数量、工厂数量和产品数量分别组合而成，且每种组合各有5个不同值的实例，共计900个。同时，本研究将HIG与IG[9]、ILS[11]、H11、H12、H21、H22、H31、H32[12]进行了比较。本试验考虑平均相对百分偏差(average relative percent deviation,ARPD)来评估调度序列π的质量。其定义为：

(1)

试验使用了蒙特卡洛试验方法。所有实例均独立运行21次。试验结果对比如图4所示。

图4 试验结果对比图Fig.4 Comparison of test results

4.2 结果分析

为了分析HIG算法在不同类型问题下的性能及与各对比算法是否存在显著性差异，对比HIG算法和各对比算法在95%置信区间的差异。95%置信区间的均值如图5所示。

图5 95%置信区间的均值图Fig.5 Means plot with 95% confidence interval

图5中:横轴为试验中涉及的9种算法；纵轴为各算法在不同问题实例情况下的ARPD值。由图5可知，本文提出的HIG算法在95%的置信区间的ARPD值明显优于其他8种对比算法。该比较结果具有统计学意义。

此外，试验对比了不同工件数量、机器数量、产品数量、工厂数量划分情况下9种算法ARPD值的概率图。95%置信区间下的概率如图6所示。

图6 95%置信区间下的概率图Fig.6 Probability with 95% confidence interval

由图6可知HIG算法的效果：在满足正态分布的前提下，HIG算法的均值和方差都是9种试验算法中最优的。此试验结果同样具有统计学意义。

为了将HIG算法与8个对比算法进行分别比较，在本研究中采用Wilcoxon符号检验进行试验结果的统计学分析。Wilcoxon试验结果如表5所示。由表5可知，在90%和95%的置信区间内，p值远小于∂的值，因此符号检验的假设成立。即，在90%和95%的置信区间内，HIG算法分别显著优于IG、ILS、H11、H12、H21、H22、H31、H32算法。此试验进一步论证了本研究所提HIG算法在解决DABFSP时的优越性。

表5 Wilcoxon试验结果

此外，为了将HIG算法与IG、ILS、H11、H12、H21、H22、H31、H32算法共同比较，本文也采用了Friedman检验。Friedman检验是用于确定多个相关样本的显著性差异的统计学检验方式，可有效反映算法之间的性能差异。

Friedman试验结果如表6所示。

表6 Friedman试验结果

由表6可知，解决DABFSP时，在95%的置信区间下，HIG算法的性能具有统计学意义的显著性优势。

5 结论

本文研究了DABFSP，并以总装配完成时间为优化目标提出了HIG算法。首先，在HIG算法的初始化阶段，采用问题驱动的构造式方法生成初始解。其次，在HIG算法的破坏-重构阶段，采用基于邻域信息的交换策略更新可行解。接着，在HIG算法的局部搜索阶段，使用基于邻域结构的插入操作进一步更新可行解。最后，在HIG算法的可行解接收阶段，以一定概率接收差解进入下一代，从而避免算法早熟收敛。

本文在试验阶段选取了以不同工件数、机器数、工厂数和产品数为组合的共计900个问题实例，测试和比较了HIG算法和其他8种先进对比算法的性能。通过针对于试验结果的统计学分析，能够得出结论：HIG算法相较于其他8种对比算法，在求解DABFSP时具有显著性的优点。本文提出的HIG算法为解决DABFSP提供了新的方案。

虽然本文提出的算法在求解900个小规模DABFSP上具有显著性的优势，但是将HIG应用于带有其他约束条件的DABFSP的解决上还具有很大的研究空间。下一步主要研究方向将集中在带有其他约束条件的DABFSP。